2022-2023学年高一上学期数学人教A版(2019)必修第一册5.7第1课时 三角函数的应用(一)课件(30张PPT)
文档属性
| 名称 | 2022-2023学年高一上学期数学人教A版(2019)必修第一册5.7第1课时 三角函数的应用(一)课件(30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 888.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 22:43:17 | ||
图片预览









文档简介
现实生活中存在大量具有周而复始、循环往复特点的周期运动变化现象,如果某种变化着的现象具有周期性, 那么就可以考虑借助三角函数来描述.
本节通过几个具体实例,说明三角函数模型的简单应用.
三角函数的应用(一)
学习目标
1.了解生活中具有周而复始、循环往复特点的现象.
2.通过构建三角函数模型,尝试解决物理中的简单问题.
简谐运动
一
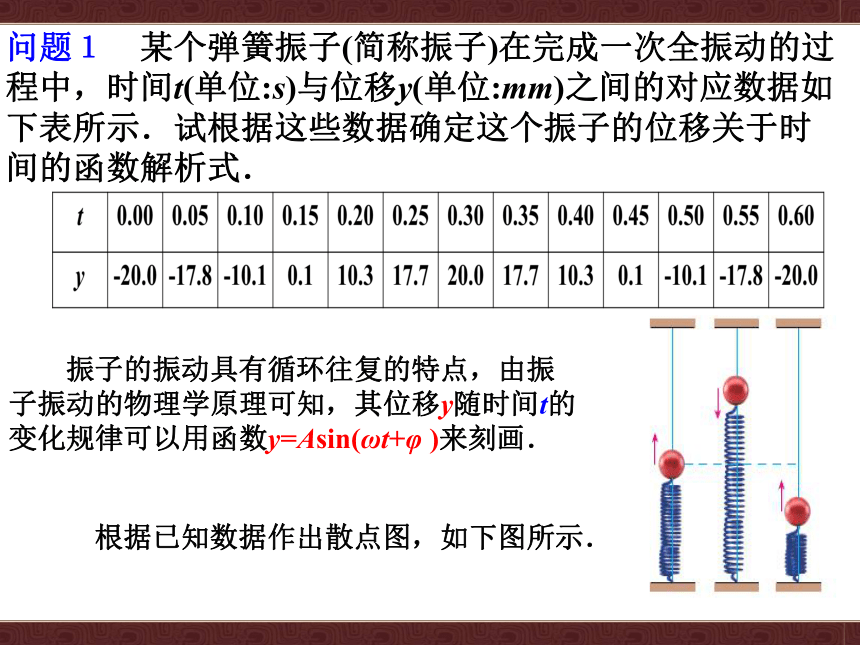
问题1 某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据如下表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
振子的振动具有循环往复的特点,由振子振动的物理学原理可知,其位移y随时间t的变化规律可以用函数y=Asin(ωt+φ )来刻画.
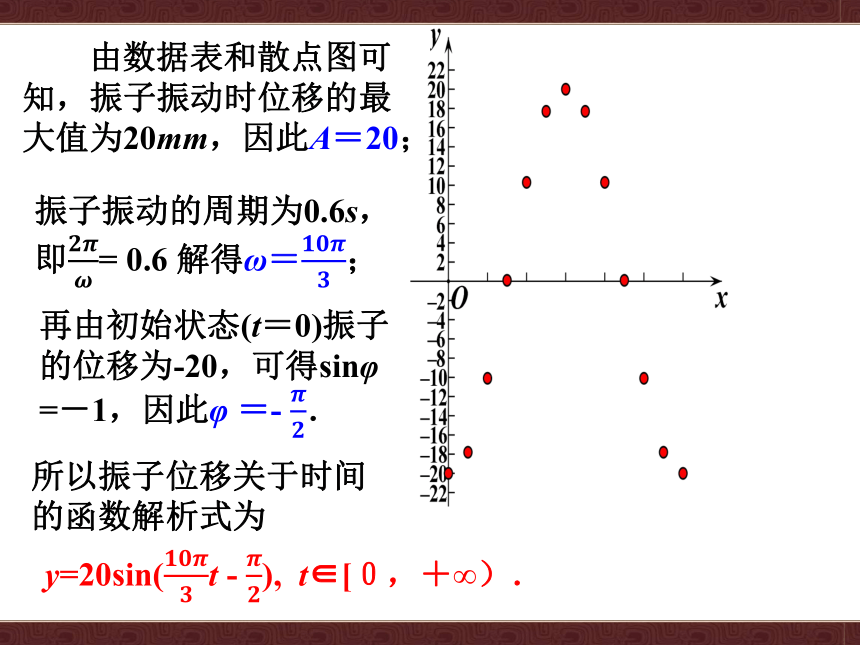
根据已知数据作出散点图,如下图所示.
所以振子位移关于时间的函数解析式为
由数据表和散点图可知,振子振动时位移的最大值为20mm,因此A=20;
振子振动的周期为0.6s,即????????????= 0.6 解得ω=????????????????;
?
再由初始状态(t=0)振子的位移为-20,可得sinφ =-1,因此φ =- ????????.
?
y=20sin(????????????????t - ????????), t∈[0,+∞).
?
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动,等等.这些都是物体在某一中心位置附近循环往复的运动.
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.
在适当的直角坐标系下,简谐运动可以用函数y=Asin(ωx+φ) , x∈[0,+∞)表示,其中A>0, ω>0.
描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
简谐运动可以用函数表示为:
y=Asin(ωx+φ) , x∈[0, +∞) , 其中A>0, ω>0.
A就是这个简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;
这个简谐运动的周期是T=????????????,它是做简谐运动的物体往复运动一次所需要的时间;
?
这个简谐运动的频率由公式????=????????=????????????给出,它是做简谐运动的物体在单位时间内往复运动的次数;
?
ωx+φ称为相位;x=0时的相位φ 称为初相.
反思感悟
若y=Asin(ωx+φ)是一个简谐运动的解析式,则A>0,ω>0,若A,ω不满足条件,则利用诱导公式变形,使之满足,再根据概念求值.
3πx-π
跟踪训
2.弹簧振子的振幅为2 cm,在6 s内振子通过的路程是32 cm,由此可知该振子振动的
A.频率为1.5 Hz B.周期为1.5 s
C.周期为6 s D.频率为6 Hz
√
三角函数在物理中的应用
二
反思感悟
处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
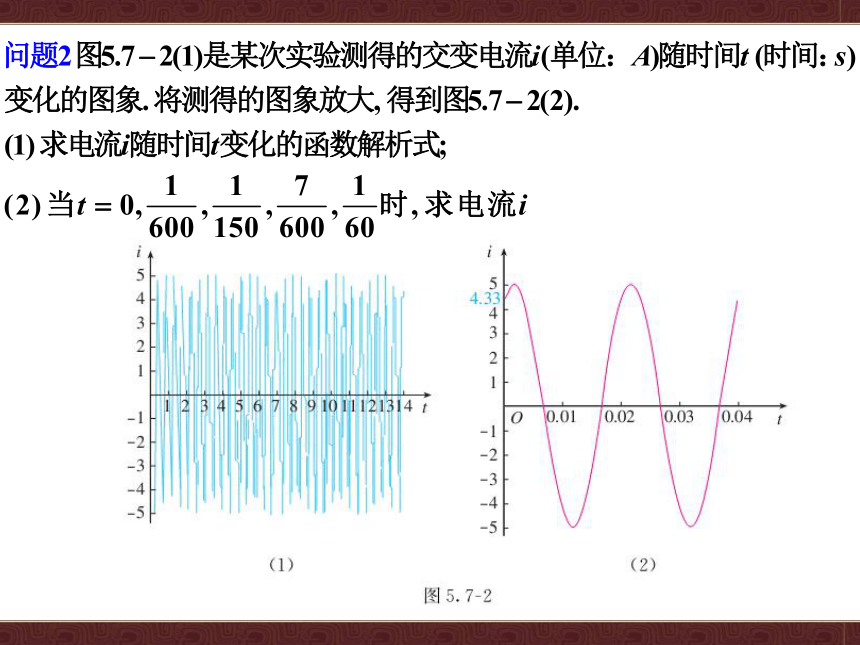
已知电流I与时间t的关系为I=Asin(ωt+φ).
跟踪训练3
由题图可知A=300,
∴ω≥300π>942,又ω∈N*,
故所求最小正整数ω=943.
三角函数“拟合”模型的应用
三
例2 海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.表5.7-2是某港口某天的时刻与水深关系的预报.
时刻
水深/m
时刻
水深/m
时刻
水深/m
0:00
5.0
9:18
2.5
18:36
5.0
3:06
7.5
12:24
5.0
21:42
2.5
6:12
5.0
15:30
7.5
24:00
4.0
(1) 选用一个函数来近似描述这一天该港口的水深与时间的关系,给出整点时水深的近似数值(精确到0.001m)
由上述关系式易得港口在整点时水深的近似值(表5.7-3):
时刻
0
1
2
3
4
5
6
7
8
9
10
11
水深/m
5.000
6.213
7.122
7.497
7.245
6.428
5.253
4.014
3.023
2.529
2.656
3.372
时刻
12
13
14
15
16
17
18
19
20
21
22
23
水深/m
4.497
5.748
6.812
7.420
7.420
6.812
5.748
4.497
3.372
2.656
2.529
3.023
(2)一条货船的吃水深度(船底与水面的距离)为4 m,安全条例规定至少要有1.5 m的安全间隙 (船底与洋底的距离),该船这一天何时能进入港口?在港口能呆多久?
由计算器可得
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;或在下午13时左右进港,下午18时左右出港.每次可以在港口停留5小时左右.
(3)某船的吃水深度为4 m,安全间隙为1.5 m,该船这一天在2:00开始卸货,吃水深度以0.3m/h的速度减少,如果这条船停止卸货后需0.4 h才能驶到深水域,那么该船最好在什么时间停止卸货,将船驶向较深的水域?
在同一直角坐标系内画出这两个函数的图象,可以看到在6~8时之间两个函数图象有一个交点
因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域.
反思感悟
处理曲线拟合与预测问题时,通常需要以下几个步骤
(1)根据原始数据绘出散点图.
(2)通过观察散点图,画出与其“最贴近”的直线或曲线,即拟合直线或拟合曲线.
(3)根据所学函数知识,求出拟合直线或拟合曲线的函数解析式.
(4)利用函数解析式,根据条件对所给问题进行预测和控制,以便为决策和管理提供依据.
三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.
具体地,我们可以利用搜集到的数据,先画出相应的 “散点图”、观察散点图,然后进行函数拟合获得具体的函数模型,最后利用这个函数模型来解决相应的实际问题.
实际问题通常涉及复杂的数据,因此往往需要使用信息技术.
课堂
小结
1.知识清单:
(1)简谐运动.
(2)函数的“拟合”.
(3)三角函数在物理中的应用.
2.方法归纳:数学建模、数形结合.
3.常见误区:选择三角函数模型时,最后结果忘记回归实际问题.
本节通过几个具体实例,说明三角函数模型的简单应用.
三角函数的应用(一)
学习目标
1.了解生活中具有周而复始、循环往复特点的现象.
2.通过构建三角函数模型,尝试解决物理中的简单问题.
简谐运动
一
问题1 某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据如下表所示.试根据这些数据确定这个振子的位移关于时间的函数解析式.
振子的振动具有循环往复的特点,由振子振动的物理学原理可知,其位移y随时间t的变化规律可以用函数y=Asin(ωt+φ )来刻画.
根据已知数据作出散点图,如下图所示.
所以振子位移关于时间的函数解析式为
由数据表和散点图可知,振子振动时位移的最大值为20mm,因此A=20;
振子振动的周期为0.6s,即????????????= 0.6 解得ω=????????????????;
?
再由初始状态(t=0)振子的位移为-20,可得sinφ =-1,因此φ =- ????????.
?
y=20sin(????????????????t - ????????), t∈[0,+∞).
?
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动,等等.这些都是物体在某一中心位置附近循环往复的运动.
在物理学中,把物体受到的力(总是指向平衡位置)正比于它离开平衡位置的距离的运动称为“简谐运动”.
在适当的直角坐标系下,简谐运动可以用函数y=Asin(ωx+φ) , x∈[0,+∞)表示,其中A>0, ω>0.
描述简谐运动的物理量,如振幅、周期和频率等都与这个解析式中的常数有关:
简谐运动可以用函数表示为:
y=Asin(ωx+φ) , x∈[0, +∞) , 其中A>0, ω>0.
A就是这个简谐运动的振幅,它是做简谐运动的物体离开平衡位置的最大距离;
这个简谐运动的周期是T=????????????,它是做简谐运动的物体往复运动一次所需要的时间;
?
这个简谐运动的频率由公式????=????????=????????????给出,它是做简谐运动的物体在单位时间内往复运动的次数;
?
ωx+φ称为相位;x=0时的相位φ 称为初相.
反思感悟
若y=Asin(ωx+φ)是一个简谐运动的解析式,则A>0,ω>0,若A,ω不满足条件,则利用诱导公式变形,使之满足,再根据概念求值.
3πx-π
跟踪训
2.弹簧振子的振幅为2 cm,在6 s内振子通过的路程是32 cm,由此可知该振子振动的
A.频率为1.5 Hz B.周期为1.5 s
C.周期为6 s D.频率为6 Hz
√
三角函数在物理中的应用
二
反思感悟
处理物理学问题的策略
(1)常涉及的物理学问题有单摆、光波、电流、机械波等,其共同的特点是具有周期性.
(2)明确物理概念的意义,此类问题往往涉及诸如频率、振幅等概念,因此要熟知其意义并与对应的三角函数知识结合解题.
已知电流I与时间t的关系为I=Asin(ωt+φ).
跟踪训练3
由题图可知A=300,
∴ω≥300π>942,又ω∈N*,
故所求最小正整数ω=943.
三角函数“拟合”模型的应用
三
例2 海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.表5.7-2是某港口某天的时刻与水深关系的预报.
时刻
水深/m
时刻
水深/m
时刻
水深/m
0:00
5.0
9:18
2.5
18:36
5.0
3:06
7.5
12:24
5.0
21:42
2.5
6:12
5.0
15:30
7.5
24:00
4.0
(1) 选用一个函数来近似描述这一天该港口的水深与时间的关系,给出整点时水深的近似数值(精确到0.001m)
由上述关系式易得港口在整点时水深的近似值(表5.7-3):
时刻
0
1
2
3
4
5
6
7
8
9
10
11
水深/m
5.000
6.213
7.122
7.497
7.245
6.428
5.253
4.014
3.023
2.529
2.656
3.372
时刻
12
13
14
15
16
17
18
19
20
21
22
23
水深/m
4.497
5.748
6.812
7.420
7.420
6.812
5.748
4.497
3.372
2.656
2.529
3.023
(2)一条货船的吃水深度(船底与水面的距离)为4 m,安全条例规定至少要有1.5 m的安全间隙 (船底与洋底的距离),该船这一天何时能进入港口?在港口能呆多久?
由计算器可得
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;或在下午13时左右进港,下午18时左右出港.每次可以在港口停留5小时左右.
(3)某船的吃水深度为4 m,安全间隙为1.5 m,该船这一天在2:00开始卸货,吃水深度以0.3m/h的速度减少,如果这条船停止卸货后需0.4 h才能驶到深水域,那么该船最好在什么时间停止卸货,将船驶向较深的水域?
在同一直角坐标系内画出这两个函数的图象,可以看到在6~8时之间两个函数图象有一个交点
因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域.
反思感悟
处理曲线拟合与预测问题时,通常需要以下几个步骤
(1)根据原始数据绘出散点图.
(2)通过观察散点图,画出与其“最贴近”的直线或曲线,即拟合直线或拟合曲线.
(3)根据所学函数知识,求出拟合直线或拟合曲线的函数解析式.
(4)利用函数解析式,根据条件对所给问题进行预测和控制,以便为决策和管理提供依据.
三角函数作为描述现实世界中周期现象的一种数学模型,可以用来研究很多问题,在刻画周期变化规律、预测其未来等方面都发挥着十分重要的作用.
具体地,我们可以利用搜集到的数据,先画出相应的 “散点图”、观察散点图,然后进行函数拟合获得具体的函数模型,最后利用这个函数模型来解决相应的实际问题.
实际问题通常涉及复杂的数据,因此往往需要使用信息技术.
课堂
小结
1.知识清单:
(1)简谐运动.
(2)函数的“拟合”.
(3)三角函数在物理中的应用.
2.方法归纳:数学建模、数形结合.
3.常见误区:选择三角函数模型时,最后结果忘记回归实际问题.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
