第三章 圆单元检测卷(含解析)
图片预览




文档简介
圆
一、单选题
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
2.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A. B.2 C.2 D.3
3.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm B. cm C.2.5cm D. cm
4.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5 cm或6.5 cm
B.2.5 cm
C.6.5 cm
D.5 cm或13cm
5.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.2cm B.4 cm
C.2cm或4cm D.2cm或4cm
6.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
7.如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
8.已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
9.若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为 ( )
A.120° B.180° C.240° D.300°
10.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB B.CE=EO C.∠OCE=40° D.∠BOC=2∠BAD
11.如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )
A.30° B.35° C.40° D.50°
12.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
13.如下图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
14.如图,将半径为的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.4cm B.2cm C.cm D.cm
15.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A. B. C. D.
16.如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
A.5 B.6 C.2 D.3
17.已知正六边形的边长是2,则该正六边形的边心距是( )
A.1 B. C.2 D.
18.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.6 B.6 C.3 D.3
19.如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为( )
A.6 B.6 C.8 D.8
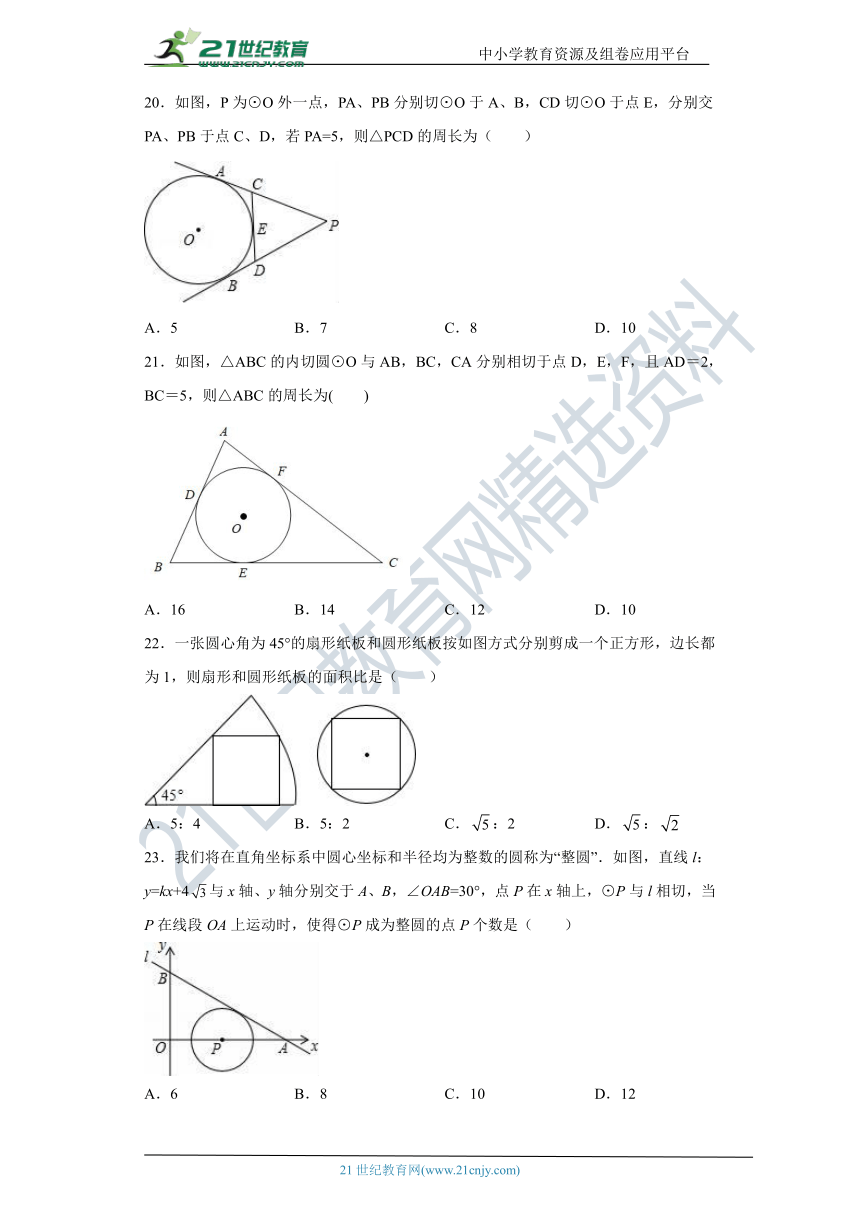
20.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )
A.5 B.7 C.8 D.10
21.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
22.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4 B.5:2 C.:2 D.:
23.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
A.6 B.8 C.10 D.12
24.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.﹣ B.﹣2 C.π﹣ D.﹣
二、填空题
25.已知一个多边形的每一个外角都等于,则这个多边形的边数是_________.
26.⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为_____.
27.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为_______.
28.如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO、BD,则∠OBD的度数是_____.
29.如图,中,,,,则的内切圆半径为________.
30.如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为,则勒洛三角形的周长为_____.
31.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为_____.
32.如图,的半径为4,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最小值为 __.
三、解答题
33.如图,AB为⊙O的直径,C、D为⊙O上的两个点,==,连接AD,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)若直径AB=6,求AD的长.
34.如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF和AD.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠EAC=60°,求AD的长.
35.如图,内接于,是的直径,为上一点,,延长交于点,.
(1)求证:是的切线;
(2)若,,求的长.
36.如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
37.如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)
38.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
39.如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
40.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
41.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
42.如图,AB为的直径,弦,垂足为点P,直线BF与AD延长线交于点F,且.
(1)求证:直线BF是的切线;
(2)若,,求的半径.
43.如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求sinE的值.
44.如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3,求弦AD的长.
45.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若∠DAB=60°,⊙O的半径为3,求线段CD的长.
46.如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E,
(1)求证:BC平分∠ABD
(2)若DC=8,BE=4,求圆的直径.
47.如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.
48.如图,已知,在ABC中,O为AB上一点,CO平分∠ACB,以O为圆心,OB长为半径作⊙O,⊙O与BC相切于点B,交CO于点D,延长CO交⊙O于点E,连接BD,BE.
(1)求证:AC是⊙O的切线.
(2)若tan∠BDE,BC=6,求⊙O的半径.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】首先圆上取一点A,连接AB,AD,根据圆的内接四边形的性质,即可得∠BAD+∠BCD=180°,即可求得∠BAD的度数,再根据圆周角的性质,即可求得答案.
【详解】圆上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°.
故选D.
【点睛】此题考查了圆周角的性质与圆的内接四边形的性质.此题比较简单,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
2.C
【分析】直接利用垂径定理进而结合圆周角定理得出△ODB是等腰直角三角形,进而得出答案.
【详解】解:∵半径OC⊥弦AB于点D,
∴,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=4,
∴DB=OD=2,
则半径OB等于:.
故选C.
【点睛】此题主要考查了垂径定理和圆周角定理,正确得出△ODB是等腰直角三角形是解题关键.
3.D
【详解】分析:根据垂径定理得出OE的长,进而利用勾股定理得出BC的长,再利用相似三角形的判定和性质解答即可.
详解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3,
∴OB=3+2=5,
∴EC=5+3=8.
在Rt△EBC中,BC=.
∵OF⊥BC,
∴∠OFC=∠CEB=90°.
∵∠C=∠C,
∴△OFC∽△BEC,
∴,即,
解得:OF=.
故选D.
点睛:本题考查了垂径定理,关键是根据垂径定理得出OE的长.
4.A
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【详解】解:当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是13cm,因而半径是6.5cm;
当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是5cm,因而半径是2.5cm.
故选A.
【点睛】本题考查了点与圆的位置关系,注意分两种情况进行讨论是解决本题的关键.
5.C
【详解】连接AC,AO,
∵O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4cm,OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM==3cm,
∴CM=OC+OM=5+3=8cm,
∴AC=cm;
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5 3=2cm,
在Rt△AMC中,AC=cm.
故选:C.
6.B
【分析】先根据圆内接四边形的性质求出∠ADC的度数,再由圆周角定理得出∠DCE的度数,根据三角形外角的性质即可得出结论.
【详解】∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
【点睛】本题考查圆内接四边形的性质,圆周角定理.圆内接四边形对角互补.在同圆或等圆中,同弧或等弧所对的圆心角相等,而同弧所对的圆周角等于圆心角的一半,所以在同圆或等圆中,同弧或等弧所对的圆周角相等.
7.B
【详解】【分析】根据圆内接四边形的性质求出∠A,再根据圆周角定理进行解答即可.
【详解】∵四边形ABCD为⊙O的内接四边形,
∴∠A=180°﹣∠BCD=180°-120°=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选B.
【点睛】本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
8.B
【分析】⊙O最长的弦就是直径从而不难求得半径的长.
【详解】解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
【点睛】本题考查弦,直径等知识,记住圆中的最长的弦就是直径是解题的关键.
9.B
【详解】试题分析:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=πr2,侧面面积=πrR,
∵侧面积是底面积的2倍,
∴2πr2=πrR,
∴R=2r,
设圆心角为n,有=2πr=πR,
∴n=180°.
故选B.
考点:圆锥的计算
10.D
【详解】∵AB是直径,CD是弦,AB⊥CD,
∴ ,
∵∠BAD是所对的圆周角,∠COB是 所对的圆心角,
∴,
故选D.
【点睛】本题考查了垂径定理、圆周角定理,熟记定理的内容并结合图形进行解题是关键.
11.C
【分析】欲求∠B的度数,需求出同弧所对的圆周角∠C的度数;△APC中,已知了∠A及外角∠APD的度数,即可由三角形的外角性质求出∠C的度数,由此得解.
【详解】解:∵∠APD是△APC的外角,
∴∠APD=∠C+∠A;
∵∠A=30°,∠APD=70°,
∴∠C=∠APD-∠A=40°;
∴∠B=∠C=40°;
故选C.
【点睛】此题主要考查了圆周角定理的应用及三角形的外角性质.熟练掌握定理及性质是解题的关键.
12.C
【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA-AP=2,接着在Rt△OPH中根据含30°的直角三角形的性质计算出OH=OP=1,然后在Rt△OHC中利用勾股定理计算出CH=,所以CD=2CH=2.
【详解】作OH⊥CD于H,连结OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=30°,∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故选C.
【点睛】本题主要考查圆中的计算问题,熟练掌握垂径定理、含30°的直角三角形的性质以及勾股定理等知识点,掌握数形结合的思想是解答的关键
13.C
【详解】解:如图,过C作CM⊥AB,交AB于点M,
由垂径定理可得M为AD的中点,
∵,且AC=3,BC=4,AB=5,
∴.
在Rt△ACM中,根据勾股定理得:,
∴
(舍去负值).
∴.
故选C.
14.A
【分析】连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,根据折叠的性质及垂径定理得到AE=BE,再根据勾股定理即可求解.
【详解】如图所示,连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,
∵折叠后恰好经过圆心,
∴OE=DE,
∵半径为4,
∴OE=2,
∵OD⊥AB,
∴AE=AB,
在Rt△AOE中,AE==2
∴AB=2AE=4
故选A.
【点睛】此题主要考查垂径定理,解题的关键是熟知垂径定理的应用.
15.A
【详解】解:连接OE,OF,ON,OG,
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5-2-MN=3-MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(3+NM)2=(3-NM)2+42,
∴NM=,
∴DM=3+=,
故选A.
16.C
【详解】试题解析:如图作DH⊥AB于H,连接BD,延长AO交BD于E.
∵菱形ABCD的边AB=20,面积为320,
∴AB DH=32O,
∴DH=16,
在Rt△ADH中,AH==12,
∴HB=AB﹣AH=8,
在Rt△BDH中,BD=,
设⊙O与AB相切于F,连接AF.
∵AD=AB,OA平分∠DAB,
∴AE⊥BD,
∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,
∴△AOF∽△DBH,
∴,
∴,
∴OF=2.
故选C.
考点:1.切线的性质;2.菱形的性质.
17.B
【分析】正六边形的边长与外接圆的半径相等,构建直角三角形,利用直角三角形的边角关系即可求出.
【详解】如图,连接OA,作OM⊥AB.
∵正六边形ABCDEF的边长为2,∴∠AOM=30°,AMAB2=1,∴正六边形的边心距是OM.
故选B.
【点睛】本题考查了正多边形的计算,正多边形的计算常用的方法是转化为直角三角形的计算.
18.A
【分析】根据垂径定理先求BC一半的长,再求BC的长.
【详解】解:如图所示,设OA与BC相交于D点
∵AB=OA=OB=6,
∴△OAB是等边三角形
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD=
所以BC=2BD=
故选:A.
【点睛】本题主要考查垂径定理和勾股定理. 解题的关键在于要利用好题中的条件圆O与圆A的半径相等,从而得出△OAB是等边三角形,为后继求解打好基础.
19.B
【分析】作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,首先利用勾股定理求得OM的长,然后判定四边形OMPN是正方形,求得正方形的对角线的长即可求得OP的长.
【详解】作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
∵AB=CD=16,
∴BM=DN=8,
∴OM=ON==6,
∵AB⊥CD,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=.
故选B.
【点睛】本题考查的是垂径定理,正方形的判定与性质及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
20.D
【分析】由切线长定理可得PA=PB, CA=CE,DE=DB, 由于△PCD的周长=PC+CE+ED+PD, 所以△PCD的周=PC+CA+BD+PD=PA+PB=2PA, 故可求得三角形的周长.
【详解】解:PA、PB为圆的两条相交切线,
PA=PB,
同理可得: CA=CE, DE=DB.
△PCD的周长=PC+CE+ED+PD,
△PCD的周长=PC+CA+BD+PD=PA+PB=2PA,
△PCD的周长=10,
故选D
【点睛】本题考查了切线的性质以及切线长定理的运用.
21.B
【分析】根据切线长定理进行求解即可.
【详解】解:∵△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,
∴AF=AD=2,BD=BE,CE=CF,
∵BE+CE=BC=5,
∴BD+CF=BC=5,
∴△ABC的周长=2+2+5+5=14,
故选B.
【点睛】本题考查了三角形的内切圆以及切线长定理,熟练掌握切线长定理是解题的关键.
22.A
【分析】先画出图形,分别求出扇形和圆的半径,再根据面积公式求出面积,最后求出比值即可.
【详解】如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=,AB=BC=CD=1,
∵∠AOB=,
∴OB=AB=1,
由勾股定理得:OD=,
∴扇形的面积是;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=,MB=MC,
∴∠MCB=∠MBC=,
∵BC=1,
∴MC=MB=,
∴⊙M的面积是,
∴扇形和圆形纸板的面积比是,
故选:A.
【点睛】本题考察圆内接四边形的性质、正方形的性质、扇形的面积公式,求出扇形和圆的面积是解题的关键.
23.A
【详解】∵直线l:y=kx+4与x轴、y轴分别交于A、B,
∴B(0,4),
∴OB=4,
在RT△AOB中,∠OAB=30°,
∴OA=OB=×4=12,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,
∴PM=PA,
设P(x,0),
∴PA=12-x,
∴⊙P的半径PM=PA=6-x,
∵x为整数,PM为整数,
∴x可以取0,2,4,6,8,10,6个数,
∴使得⊙P成为整圆的点P个数是6.
故选A.
【点睛】考点:1.切线的性质;2.一次函数图象上点的坐标特征.
24.A
【分析】过O作OECD于点E,根据AB是⊙O的切线,得出∠ABO=90°,求出即可.
【详解】如图,过O作OECD于点E,
AB是⊙O的切线,
∠ABO=90°,
∠A=30°,
∠AOB=60°,
∠COD=120°,
OC=OD=2,
,
OE=1,CD=2DE=,
.
故选A.
【点睛】本题考查扇形的面积,三角形的面积,阴影部分的面积,掌握扇形的面积,三角形的面积,阴影部分的面积世界关键.
25.5
【详解】∵多边形的每个外角都等于72°,
∵多边形的外角和为360°,
∴360°÷72°=5,
∴这个多边形的边数为5.
故答案为5.
26.3或1
【分析】根据垂径定理推论,得AO⊥BC,由勾股定理得OD=1,分两种情况分别求出AD的值,即可
【详解】如图所示:∵⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,
∴,
∴AO⊥BC,
∴BD=BC=,
在Rt△OBD中,
∵BD2+OD2=OB2,即()2+OD2=22,解得OD=1,
∴当如图1所示时,AD=OA﹣OD=2﹣1=1;
当如图2所示时,AD=OA+OD=2+1=3.
故答案为1或3.
【点睛】本题主要考查垂径定理和勾股定理,掌握垂径定理和勾股定理是解题的关键.
27.(3,2).
【分析】过点P作PD⊥x轴于点D,连接OP,先由垂径定理求出OD的长,再根据勾股定理求出PD的长,故可得出答案.
【详解】过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,
∴OD=OA=3,
在Rt△OPD中 ∵OP= OD=3,
∴PD=2
∴P(3,2) .
故答案为(3,2).
【点睛】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
28.30°
【分析】根据点的坐标得到OD,OC的长度,利用勾股定理求出CD的长度,由此求出∠OCD的度数;由于∠OBD和∠OCD是弧OD所对的圆周角,根据“同弧所对的圆周角相等”求出∠OBD的度数.
【详解】连接CD.
由题意得∠COD=90°,
∴CD是⊙A的直径.
∵D(0,1),C(,0),
∴OD=1,OC=,
∴CD==2,
∴∠OCD=30°,
∴∠OBD=∠OCD=30°.(同弧或等弧所对的圆周角相等)
故答案为30°.
【点睛】本题考查圆周角定理以及推论,可以结合圆周角进行解答.
29.
【分析】先由勾股定理求出AB的长,再根据切线性质和正方形的判定这证得四边形OECF是正方形,然后利用切线长定理求得半径r即可.
【详解】如图,
∵在,,,
∴由勾股定理得:,
∵圆O为的内切圆,
∴,;
四边形是正方形;
由切线长定理,得:,,;
,
即:,
故答案为:2.
【点睛】本题考查了切线的性质、正方形的判定与性质、切线长定理、勾股定理,熟练掌握切线性质和切线长定理是解答的关键.
30.πa
【分析】首先根据等边三角形的性质得出∠A=∠B=∠C=60°,AB=BC=CA=a,再利用弧长公式求出的长=的长=的长=,那么勒洛三角形的周长为
【详解】解:如图.∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=CA=a,
∴的长=的长=的长=,
∴勒洛三角形的周长为
故答案为:πa.
【点睛】本题考查了弧长公式,解题的关键是掌握(弧长为l,圆心角度数为n,圆的半径为R),也考查了等边三角形的性质.
31. .
【分析】当PC⊥AB时,线段PQ最短;连接CP、CQ,根据勾股定理知PQ2=CP2﹣CQ2,先求出CP的长,然后由勾股定理即可求得答案.
【详解】连接CP、CQ;如图所示:
∵PQ是⊙C的切线,∴CQ⊥PQ,∠CQP=90°,根据勾股定理得:PQ2=CP2﹣CQ2,∴当PC⊥AB时,线段PQ最短.
∵在Rt△ACB中,∠A=30°,BC=2,∴AB=2BC=4,AC=2,∴CP===,∴PQ==,∴PQ的最小值是.
故答案为.
【点睛】本题考查了切线的性质以及勾股定理的运用;注意掌握辅助线的作法,注意当PC⊥AB时,线段PQ最短是关键.
32.18
【分析】由中知要使取得最小值,则需取得最小值,连接,交于点,当点位于位置时,取得最小值,据此求解可得.
【详解】解:连接,
,
,
,
,
若要使取得最小值,则需取得最小值,
连接,交于点,当点位于位置时,取得最小值,
过点作轴于点,
则,,
,
又,
,
,
故答案是:18.
【点睛】本题主要考查点与圆的位置关系,解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB取得最小值时点P的位置.
33.(1)见解析;(2)3
【分析】(1)连接OD,根据已知条件得到∠BOD=180°=60°,根据等腰三角形的性质得到∠ADO=∠DAB=30°,得到∠EDA=60°,求得OD⊥DE,于是得到结论;
(2)连接BD,根据圆周角定理得到∠ADB=90°,解直角三角形即可得到结论.
【详解】(1)证明:连接OD,
∵,
∴∠BOD=180°=60°,
∵,
∴∠EAD=∠DAB=BOD=30°,
∵OA=OD,
∴∠ADO=∠DAB=30°,
∵DE⊥AC,
∴∠E=90°,
∴∠EAD+∠EDA=90°,
∴∠EDA=60°,
∴∠EDO=∠EDA+∠ADO=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接BD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠DAB=30°,AB=6,
∴BD=AB=3,
∴AD==3.
【点睛】本题考查了切线的证明,及线段长度的计算,熟知圆的性质及切线的证明方法,以及含30°角的直角三角形的特点是解题的关键.
34.(1)见解析;(2)AD=.
【分析】(1)连接FO,可根据三角形中位线的性质可判断易证OF∥AB,然后根据直径所对的圆周角是直角,可得CE⊥AE,进而知OF⊥CE,然后根据垂径定理可得∠FEC=∠FCE,∠OEC=∠OCE,再通过Rt△ABC可知∠OEC+∠FEC=90°,因此可证FE为⊙O的切线;
(2)在Rt△OCD中和Rt△ACD中,分别利用勾股定理分别求出CD,AD的长即可 .
【详解】
(1)证明:连接CE,如图所示:
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°,
∵点F为BC的中点,
∴EF=BF=CF,
∴∠FEC=∠FCE,
∵OE=OC,
∴∠OEC=∠OCE,
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°,
∴EF是⊙O的切线.
(2)解:∵OA=OE,∠EAC=60°,
∴△AOE是等边三角形.
∴∠AOE=60°,
∴∠COD=∠AOE=60°,
∵⊙O的半径为2,
∴OA=OC=2
在Rt△OCD中,∵∠OCD=90°,∠COD=60°,
∴∠ODC=30°,
∴OD=2OC=4,
∴CD=.
在Rt△ACD中,∵∠ACD=90°,AC=4,CD=.
∴AD==.
【点睛】本题主要考查直角三角形、全等三角形的判定与性质以及与圆有关的位置关系 .
35.(1)见解析;(2)
【分析】(1)根据,可得,根据对顶角相等可得,进而可得,根据,可得,结合,根据角度的转化可得,进而即可证明是的切线;
(2)根据,可得,设,则,分别求得,进而根据勾股定理列出方程解方程可得,进而根据即可求得.
【详解】(1),
,
,
,
,
,
是直径,
,
,
是的切线;
(2),
,
,
设,则,
,,
在中,,
即,
解得(舍去),
.
【点睛】本题考查了切线的判定,勾股定理解直角三角形,正切的定义,利用角度相等则正切值相等将已知条件转化是解题的关键.
36.(1)证明见解析;(2)证明见解析;
【分析】(1)连接AD,根据中垂线定理不难求得AB=AC;
(2)要证DE为⊙O的切线,只要证明∠ODE=90°即可.
【详解】(1)连接AD;
∵AB是⊙O的直径,
∴∠ADB=90°.
又∵DC=BD,
∴AD是BC的中垂线.
∴AB=AC.
(2)连接OD;
∵OA=OB,CD=BD,
∴OD∥AC.
∴∠ODE=∠CED.
又∵DE⊥AC,
∴∠CED=90°.
∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
【点睛】考点:切线的判定
37.(1)证明见解析 (2)﹣6π
【分析】(1)直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF,即可得出答案;
(2)直接利用条件得出S△ACD=S△COD,再利用S阴影=S△AED﹣S扇形COD求出答案.
【详解】(1)证明:连接OD,
∵D为弧BC的中点,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∵DE⊥AC,
∴∠E=90°,
∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF,
∴EF为半圆O的切线;
(2)解:连接OC与CD,
∵DA=DF,
∴∠BAD=∠F,
∴∠BAD=∠F=∠CAD,
又∵∠BAD+∠CAD+∠F=90°,
∴∠F=30°,∠BAC=60°,
∵OC=OA,
∴△AOC为等边三角形,
∴∠AOC=60°,∠COB=120°,
∵OD⊥EF,∠F=30°,
∴∠DOF=60°,
在Rt△ODF中,DF=6,
∴OD=DF tan30°=6,
在Rt△AED中,DA=6,∠CAD=30°,
∴DE=DA sin30°=3,EA=DA cos30°=9,
∵∠COD=180°﹣∠AOC﹣∠DOF=60°,
由CO=DO,
∴△COD是等边三角形,
∴∠OCD=60°,
∴∠DCO=∠AOC=60°,
∴CD∥AB,
故S△ACD=S△COD,
∴S阴影=S△AED﹣S扇形COD==.
【点睛】此题主要考查了切线的判定,圆周角定理,等边三角形的判定与性质,解直角三角形及扇形面积求法等知识,得出S△ACD=S△COD是解题关键.
38.(1)证明见解析;(2)
【详解】分析:(1)根据平行线的性质得出∠AEO=90°,再利用垂径定理证明即可;
(2)根据弧长公式解答即可.
详证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED;
(2)∵OC⊥AD,
∴ ,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴ =.
点睛:此题考查弧长公式,关键是根据弧长公式和垂径定理解答.
39.(1) B(,2).(2)证明见解析.
【分析】(1)在Rt△ABN中,求出AN、AB即可解决问题;
(2)连接MC,NC.只要证明∠MCD=90°即可
【详解】(1)∵A的坐标为(0,6),N(0,2),
∴AN=4,
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8,
∴由勾股定理可知:NB=,
∴B(,2).
(2)连接MC,NC
∵AN是⊙M的直径,
∴∠ACN=90°,
∴∠NCB=90°,
在Rt△NCB中,D为NB的中点,
∴CD=NB=ND,
∴∠CND=∠NCD,
∵MC=MN,
∴∠MCN=∠MNC,
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°,
即MC⊥CD.
∴直线CD是⊙M的切线.
考点:切线的判定;坐标与图形性质.
40.(1)证明见解析;(2)
【分析】(1)连接OA、OD,如图,根据垂径定理的推理,由D为BE的下半圆弧的中点得到OD⊥BE,则∠D+∠DFO=90°,再由AC=FC得到∠CAF=∠CFA,根据对顶角相等得∠CFA=∠DFO,所以∠CAF=∠DFO,加上∠OAD=∠ODF,则∠OAD+∠CAF=90°,于是根据切线的判定定理即可得到AC是⊙O的切线;
(2)由于圆的半径R=5,EF=3,则OF=2,然后在Rt△ODF中利用勾股定理计算DF的长.
【详解】解:(1)连接OA、OD,如图,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,
∴∠D+∠DFO=90°,
∵AC=FC,
∴∠CAF=∠CFA,
∵∠CFA=∠DFO,
∴∠CAF=∠DFO,
而OA=OD,
∴∠OAD=∠ODF,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)∵圆的半径R=5,EF=3,
∴OF=2,
在Rt△ODF中,∵OD=5,OF=2,
∴DF=.
【点睛】本题考查切线的判定,垂径定理,勾股定理解直角三角形,解题的关键是作出辅助线.
41.(1)证明见解析;(2)6.
【详解】试题分析:(1)连接OD、CD,由AC为⊙O的直径知△BCD是直角三角形,结合E为BC的中点知∠CDE=∠DCE,由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案;
(2)设⊙O的半径为r,由OD2+DF2=OF2,即r2+42=(r+2)2可得r=3,即可得出答案.
试题解析:(1)如图,连接OD、CD.∵AC为⊙O的直径,∴△BCD是直角三角形,∵E为BC的中点,∴BE=CE=DE,∴∠CDE=∠DCE,∵OD=OC,∴∠ODC=∠OCD,∵∠ACB=90°,∴∠OCD+∠DCE=90°,∴∠ODC+∠CDE=90°,即OD⊥DE,∴DE是⊙O的切线;
(2)设⊙O的半径为r,∵∠ODF=90°,∴OD2+DF2=OF2,即r2+42=(r+2)2,解得:r=3,∴⊙O的直径为6.
考点:切线的判定与性质.
42.(1)见解析;(2)2
【分析】(1)利用圆周角定理得到.则,根据平行线的判定得,然后根据平行线的性质得,最后根据切线的判定定理可得到结论;
(2)连接,如图,根据垂径定理得到,然后利用勾股定理觉得即可.
【详解】(1)证明:,
而.
,
,
,
,
直线是的切线;
(2)解:连接,如图,
,
,
在中,,
即的半径为2.
【点睛】本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和垂径定理.解题关键是综合运用定理进行推理的能力,题目比较典型,是一道综合性比较强的题目.
43.(1)证明见解析;(2)
【详解】分析:(1)要证明是圆的切线,须证明过切点的半径垂直,所以连接OB,证明OB⊥PE即可.
(2)要求sinE,首先应找出∠E所在的直角三角形,然后利用直角三角函数求解即可.而sinE既可放在直角三角形EAP中,也可放在直角三角形EBO中,所以利用相似三角形的性质求出EP或EO的长即可解决问题
详解:(1)证明:连接OB
∵PO⊥AB,
∴AC=BC,
∴PA=PB,
在△PAO和△PBO中
,
∴△PAO和≌△PBO,
∴∠OBP=∠OAP=90°,
∴PB是⊙O的切线.
(2)连接BD,则BD∥PO,且BD=2OC=6
在Rt△ACO中,OC=3,AC=4
∴AO=5
在Rt△ACO与Rt△PAO中,
∠APO=∠APO,
∠PAO=∠ACO=90°
∴△ACO △PAO
∴
∴PO=,PA=
∴PB=PA=
在△EPO与△EBD中,
BD∥PO
∴△EPO∽△EBD
∴,
解得EB=,PE=,
∴sinE=.
点睛:本题考查了切线的判定以及相似三角形的判定和性质.能够通过作辅助线将所求的角转移到相应的直角三角形中,是解答此题的关键.
44.(1)证明见解析(2)
【分析】(1)连结OC,如图,由AD平分∠EAC得到∠1=∠3,加上∠1=∠2,则∠3=∠2,于是可判断OD∥AE,根据平行线的性质得OD⊥CE,然后根据切线的判定定理得到结论;
(2)由△CDB∽△CAD,可得,推出CD2=CB CA,可得(3)2=3CA,推出CA=6,推出AB=CA﹣BC=3,,设BD=k,AD=2k,在Rt△ADB中,可得2k2+4k2=5,求出k即可解决问题.
【详解】(1)证明:连结OC,如图,
∵AD平分∠EAC,
∴∠1=∠3,
∵OA=OD,
∴∠1=∠2,
∴∠3=∠2,
∴OD∥AE,
∵AE⊥DC,
∴OD⊥CE,
∴CE是⊙O的切线;
(2)∵∠CDO=∠ADB=90°,
∴∠2=∠CDB=∠1,∵∠C=∠C,
∴△CDB∽△CAD,
∴,
∴CD2=CB CA,
∴(3)2=3CA,
∴CA=6,
∴AB=CA﹣BC=3,,设BD=k,AD=2k,
在Rt△ADB中,2k2+4k2=5,
∴k=,
∴AD=.
45.(1)证明见解析;(2).
【分析】(1)连接OC,由OA=OC可以得到∠OAC=∠OCA,然后利用角平分线的性质可以证明∠DAC=∠OCA,接着利用平行线的判定即可得到OC∥AD,然后就得到OC⊥CD,由此即可证明直线CD与⊙O相切于C点;
(2)连接BC,∠BAC=30°,在Rt△ABC中可求得AC,同理在Rt△ACD中求得CD.
【详解】(1)证明:连接CO,
∵AO=CO,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴CO∥AD,
∴CO⊥CD,
∴DC为⊙O的切线;
(2)解:连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠DAB=60°,AC平分∠DAB,
∴∠BAC=∠DAB=30°,
∵⊙O的半径为3,
∴AB=6,
∴AC=AB=3.
∵∠CAD=30°
∴
【点睛】此题主要考查了切线的性质与判定,解题时首先利用切线的判定证明切线,然后利用含特殊角度的直角三角形求得边长即可解决问题.
46.(1)证明见解析;(2);
【分析】(1)连接OC,根据CD为切线可得OC⊥CD,再根据平行线的性质即可得出结论;
(2)连接AE交OC于G,根据圆与平行线的性质易得四边形CDEG为矩形,再根据勾股定理即可得出结论.
【详解】(1)证明:连接OC,如图,
∵CD为切线,
∴OC⊥CD,
∵BD⊥DF,
∴OC∥BD,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2,
∴∠2=∠3,
∴BC平分∠ABD;
(2)解:连接AE交OC于G,如图,
∵AB为直径,
∴∠AEB=90°,
∵OC⊥CD,ED⊥CD,
∴四边形CDEG为矩形,
∴GE=CD=8,
∵OC∥BD,
∴,
∴AE=2EG=16,
在Rt△ABE中,AB==4,
即圆的直径为4.
【点睛】本题考查了勾股定理、切线与平行线的性质,矩形的性质与判定,平行线分线段成比例定理,解题的关键是熟练的掌握勾股定理、切线与平行线的性质.
47.(1)证明见解析;(2)DE与⊙O相切;(3)
【分析】(1)连接AD,根据等腰三角形三线合一性质得到AD⊥BC,再根据90°的圆周角所对的弦为直径即可证得AB是⊙O的直径;
(2)DE与圆O相切,理由为:连接OD,利用中位线定理得到OD∥AC,利用两直线平行内错角相等得到∠ODE为直角,再由OD为半径,即可得证;
(3)由AB=AC,且∠BAC=60°,得到DABC为等边三角形,连接BF,DE为DCBF中位线,求出BF的长,即可确定出DE的长.
【详解】解:(1)证明:连接AD,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴∠ADB=90°,
∴AB为⊙O的直径;
(2)DE与⊙O相切,
理由为:连接OD,
∵O、D分别为AB、BC的中点,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∵OD为⊙O的半径,
∴DE与⊙O相切;
(3)解:连接BF,
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∴AB=AC=BC=6,
∵AB为⊙O的直径,
∴∠AFB=∠DEC=90°,
∴AF=CF=3,DE∥BF,
∵D为BC中点,
∴E为CF中点,DE=BF,
在Rt△ABF中,∠AFB=90°,AB=6,AF=3,
∴BF=,则DE=BF=.
48.(1)见解析;(2)4.5
【分析】(1)作OF⊥AC于F,利用角平分线的性质证明OF=OB,即可证明AC是⊙O的切线.
(2)利用圆周角定理证明△CBE∽△CDB,根据相似三角形的性质即可求解.
【详解】(1)证明:作OF⊥AC于F,
∵⊙O与BC相切于点B,∴OB⊥BC,
∵CO平分∠ACB,
∴OF=OB ,
又OB是半径,OF⊥AC于F,
∴AC是⊙O的切线.
(2)解:∵DE是直径,
∴∠DBE=90°,
又tan∠BDE,∴,
由(1),知∵OE=OB,OB⊥BC ,
∴∠OBC=90° ,
∴∠DBC=∠OBE,
∴∠E=∠OBE,
∴∠E=∠DBC,
又 ∠C=∠C,
∴△CBE∽△CDB,
∴,
∵BC=6,
∴,
∴,
∴DE=9,
∵OD=4.5,即⊙O的半径是4.5.
【点睛】本题考查了切线的判定和性质,相似三角形的判定和性质,正切函数,注意掌握辅助线的作法,注意数形结合思想的应用.
一、单选题
1.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
2.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=4,则半径OB等于( )
A. B.2 C.2 D.3
3.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )
A.3cm B. cm C.2.5cm D. cm
4.一个点到圆的最小距离为4cm,最大距离为9cm,则该圆的半径是( )
A.2.5 cm或6.5 cm
B.2.5 cm
C.6.5 cm
D.5 cm或13cm
5.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.2cm B.4 cm
C.2cm或4cm D.2cm或4cm
6.如图,四边形ABCD内接于⊙O,F是上一点,且,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A.45° B.50° C.55° D.60°
7.如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.120° C.100° D.90°
8.已知⊙O中最长的弦为8cm,则⊙O的半径为( )cm.
A.2 B.4 C.8 D.16
9.若一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角为 ( )
A.120° B.180° C.240° D.300°
10.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连接CO,AD,∠BAD=20°,则下列说法中正确的是( )
A.AD=2OB B.CE=EO C.∠OCE=40° D.∠BOC=2∠BAD
11.如图,⊙O中,弦AB、CD相交于点P,若∠A=30°,∠APD=70°,则∠B等于( )
A.30° B.35° C.40° D.50°
12.如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为( )
A. B.2 C.2 D.8
13.如下图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为( )
A. B. C. D.
14.如图,将半径为的圆折叠后,圆弧恰好经过圆心,则折痕的长为( )
A.4cm B.2cm C.cm D.cm
15.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A. B. C. D.
16.如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
A.5 B.6 C.2 D.3
17.已知正六边形的边长是2,则该正六边形的边心距是( )
A.1 B. C.2 D.
18.如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于B、C点,则BC=( )
A.6 B.6 C.3 D.3
19.如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为( )
A.6 B.6 C.8 D.8
20.如图,P为⊙O外一点,PA、PB分别切⊙O于A、B,CD切⊙O于点E,分别交PA、PB于点C、D,若PA=5,则△PCD的周长为( )
A.5 B.7 C.8 D.10
21.如图,△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,且AD=2,BC=5,则△ABC的周长为( )
A.16 B.14 C.12 D.10
22.一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )
A.5:4 B.5:2 C.:2 D.:
23.我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:y=kx+4与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
A.6 B.8 C.10 D.12
24.如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
A.﹣ B.﹣2 C.π﹣ D.﹣
二、填空题
25.已知一个多边形的每一个外角都等于,则这个多边形的边数是_________.
26.⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为_____.
27.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为,则点P的坐标为_______.
28.如图,⊙A过点O(0,0),C(,0),D(0,1),点B是x轴下方⊙A上的一点,连接BO、BD,则∠OBD的度数是_____.
29.如图,中,,,,则的内切圆半径为________.
30.如图,分别以等边三角形的每个顶点为圆心、以边长为半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形称为勒洛三角形.若等边三角形的边长为,则勒洛三角形的周长为_____.
31.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,⊙C的半径为1,点P是斜边AB上的点,过点P作⊙C的一条切线PQ(点Q是切点),则线段PQ的最小值为_____.
32.如图,的半径为4,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最小值为 __.
三、解答题
33.如图,AB为⊙O的直径,C、D为⊙O上的两个点,==,连接AD,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)若直径AB=6,求AD的长.
34.如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF和AD.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠EAC=60°,求AD的长.
35.如图,内接于,是的直径,为上一点,,延长交于点,.
(1)求证:是的切线;
(2)若,,求的长.
36.如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.
37.如图,AB为半圆O的直径,AC是⊙O的一条弦,D为的中点,作DE⊥AC,交AB的延长线于点F,连接DA.
(1)求证:EF为半圆O的切线;
(2)若DA=DF=6,求阴影区域的面积.(结果保留根号和π)
38.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连结BC.
(1)求证:AE=ED;
(2)若AB=10,∠CBD=36°,求的长.
39.如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.
40.如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
41.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.
42.如图,AB为的直径,弦,垂足为点P,直线BF与AD延长线交于点F,且.
(1)求证:直线BF是的切线;
(2)若,,求的半径.
43.如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求sinE的值.
44.如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3,求弦AD的长.
45.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若∠DAB=60°,⊙O的半径为3,求线段CD的长.
46.如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E,
(1)求证:BC平分∠ABD
(2)若DC=8,BE=4,求圆的直径.
47.如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.
48.如图,已知,在ABC中,O为AB上一点,CO平分∠ACB,以O为圆心,OB长为半径作⊙O,⊙O与BC相切于点B,交CO于点D,延长CO交⊙O于点E,连接BD,BE.
(1)求证:AC是⊙O的切线.
(2)若tan∠BDE,BC=6,求⊙O的半径.
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.D
【分析】首先圆上取一点A,连接AB,AD,根据圆的内接四边形的性质,即可得∠BAD+∠BCD=180°,即可求得∠BAD的度数,再根据圆周角的性质,即可求得答案.
【详解】圆上取一点A,连接AB,AD,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°.
故选D.
【点睛】此题考查了圆周角的性质与圆的内接四边形的性质.此题比较简单,解题的关键是注意数形结合思想的应用,注意辅助线的作法.
2.C
【分析】直接利用垂径定理进而结合圆周角定理得出△ODB是等腰直角三角形,进而得出答案.
【详解】解:∵半径OC⊥弦AB于点D,
∴,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=4,
∴DB=OD=2,
则半径OB等于:.
故选C.
【点睛】此题主要考查了垂径定理和圆周角定理,正确得出△ODB是等腰直角三角形是解题关键.
3.D
【详解】分析:根据垂径定理得出OE的长,进而利用勾股定理得出BC的长,再利用相似三角形的判定和性质解答即可.
详解:连接OB,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,AE=2cm.
在Rt△OEB中,OE2+BE2=OB2,即OE2+42=(OE+2)2
解得:OE=3,
∴OB=3+2=5,
∴EC=5+3=8.
在Rt△EBC中,BC=.
∵OF⊥BC,
∴∠OFC=∠CEB=90°.
∵∠C=∠C,
∴△OFC∽△BEC,
∴,即,
解得:OF=.
故选D.
点睛:本题考查了垂径定理,关键是根据垂径定理得出OE的长.
4.A
【分析】点P应分为位于圆的内部位于外部两种情况讨论.当点P在圆内时,点到圆的最大距离与最小距离的和是直径;当点P在圆外时,点到圆的最大距离与最小距离的差是直径,由此得解.
【详解】解:当点P在圆内时,最近点的距离为4cm,最远点的距离为9cm,则直径是13cm,因而半径是6.5cm;
当点P在圆外时,最近点的距离为4cm,最远点的距离为9cm,则直径是5cm,因而半径是2.5cm.
故选A.
【点睛】本题考查了点与圆的位置关系,注意分两种情况进行讨论是解决本题的关键.
5.C
【详解】连接AC,AO,
∵O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4cm,OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM==3cm,
∴CM=OC+OM=5+3=8cm,
∴AC=cm;
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5 3=2cm,
在Rt△AMC中,AC=cm.
故选:C.
6.B
【分析】先根据圆内接四边形的性质求出∠ADC的度数,再由圆周角定理得出∠DCE的度数,根据三角形外角的性质即可得出结论.
【详解】∵四边形ABCD内接于⊙O,∠ABC=105°,
∴∠ADC=180°﹣∠ABC=180°﹣105°=75°.
∵,∠BAC=25°,
∴∠DCE=∠BAC=25°,
∴∠E=∠ADC﹣∠DCE=75°﹣25°=50°.
【点睛】本题考查圆内接四边形的性质,圆周角定理.圆内接四边形对角互补.在同圆或等圆中,同弧或等弧所对的圆心角相等,而同弧所对的圆周角等于圆心角的一半,所以在同圆或等圆中,同弧或等弧所对的圆周角相等.
7.B
【详解】【分析】根据圆内接四边形的性质求出∠A,再根据圆周角定理进行解答即可.
【详解】∵四边形ABCD为⊙O的内接四边形,
∴∠A=180°﹣∠BCD=180°-120°=60°,
由圆周角定理得,∠BOD=2∠A=120°,
故选B.
【点睛】本题考查的是圆内接四边形的性质、圆周角定理,掌握圆内接四边形的对角互补是解题的关键.
8.B
【分析】⊙O最长的弦就是直径从而不难求得半径的长.
【详解】解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
【点睛】本题考查弦,直径等知识,记住圆中的最长的弦就是直径是解题的关键.
9.B
【详解】试题分析:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=πr2,侧面面积=πrR,
∵侧面积是底面积的2倍,
∴2πr2=πrR,
∴R=2r,
设圆心角为n,有=2πr=πR,
∴n=180°.
故选B.
考点:圆锥的计算
10.D
【详解】∵AB是直径,CD是弦,AB⊥CD,
∴ ,
∵∠BAD是所对的圆周角,∠COB是 所对的圆心角,
∴,
故选D.
【点睛】本题考查了垂径定理、圆周角定理,熟记定理的内容并结合图形进行解题是关键.
11.C
【分析】欲求∠B的度数,需求出同弧所对的圆周角∠C的度数;△APC中,已知了∠A及外角∠APD的度数,即可由三角形的外角性质求出∠C的度数,由此得解.
【详解】解:∵∠APD是△APC的外角,
∴∠APD=∠C+∠A;
∵∠A=30°,∠APD=70°,
∴∠C=∠APD-∠A=40°;
∴∠B=∠C=40°;
故选C.
【点睛】此题主要考查了圆周角定理的应用及三角形的外角性质.熟练掌握定理及性质是解题的关键.
12.C
【分析】作OH⊥CD于H,连结OC,如图,根据垂径定理由OH⊥CD得到HC=HD,再利用AP=2,BP=6可计算出半径OA=4,则OP=OA-AP=2,接着在Rt△OPH中根据含30°的直角三角形的性质计算出OH=OP=1,然后在Rt△OHC中利用勾股定理计算出CH=,所以CD=2CH=2.
【详解】作OH⊥CD于H,连结OC,如图,
∵OH⊥CD,
∴HC=HD,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,
∴OP=OA﹣AP=2,
在Rt△OPH中,∵∠OPH=30°,
∴∠POH=30°,∴OH=OP=1,
在Rt△OHC中,∵OC=4,OH=1,
∴CH=,
∴CD=2CH=2.
故选C.
【点睛】本题主要考查圆中的计算问题,熟练掌握垂径定理、含30°的直角三角形的性质以及勾股定理等知识点,掌握数形结合的思想是解答的关键
13.C
【详解】解:如图,过C作CM⊥AB,交AB于点M,
由垂径定理可得M为AD的中点,
∵,且AC=3,BC=4,AB=5,
∴.
在Rt△ACM中,根据勾股定理得:,
∴
(舍去负值).
∴.
故选C.
14.A
【分析】连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,根据折叠的性质及垂径定理得到AE=BE,再根据勾股定理即可求解.
【详解】如图所示,连接AO,过O作OD⊥AB,交于点D,交弦AB与点E,
∵折叠后恰好经过圆心,
∴OE=DE,
∵半径为4,
∴OE=2,
∵OD⊥AB,
∴AE=AB,
在Rt△AOE中,AE==2
∴AB=2AE=4
故选A.
【点睛】此题主要考查垂径定理,解题的关键是熟知垂径定理的应用.
15.A
【详解】解:连接OE,OF,ON,OG,
在矩形ABCD中,
∵∠A=∠B=90°,CD=AB=4,
∵AD,AB,BC分别与⊙O相切于E,F,G三点,
∴∠AEO=∠AFO=∠OFB=∠BGO=90°,
∴四边形AFOE,FBGO是正方形,
∴AF=BF=AE=BG=2,
∴DE=3,
∵DM是⊙O的切线,
∴DN=DE=3,MN=MG,
∴CM=5-2-MN=3-MN,
在Rt△DMC中,DM2=CD2+CM2,
∴(3+NM)2=(3-NM)2+42,
∴NM=,
∴DM=3+=,
故选A.
16.C
【详解】试题解析:如图作DH⊥AB于H,连接BD,延长AO交BD于E.
∵菱形ABCD的边AB=20,面积为320,
∴AB DH=32O,
∴DH=16,
在Rt△ADH中,AH==12,
∴HB=AB﹣AH=8,
在Rt△BDH中,BD=,
设⊙O与AB相切于F,连接AF.
∵AD=AB,OA平分∠DAB,
∴AE⊥BD,
∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,
∴△AOF∽△DBH,
∴,
∴,
∴OF=2.
故选C.
考点:1.切线的性质;2.菱形的性质.
17.B
【分析】正六边形的边长与外接圆的半径相等,构建直角三角形,利用直角三角形的边角关系即可求出.
【详解】如图,连接OA,作OM⊥AB.
∵正六边形ABCDEF的边长为2,∴∠AOM=30°,AMAB2=1,∴正六边形的边心距是OM.
故选B.
【点睛】本题考查了正多边形的计算,正多边形的计算常用的方法是转化为直角三角形的计算.
18.A
【分析】根据垂径定理先求BC一半的长,再求BC的长.
【详解】解:如图所示,设OA与BC相交于D点
∵AB=OA=OB=6,
∴△OAB是等边三角形
又根据垂径定理可得,OA平分BC,
利用勾股定理可得BD=
所以BC=2BD=
故选:A.
【点睛】本题主要考查垂径定理和勾股定理. 解题的关键在于要利用好题中的条件圆O与圆A的半径相等,从而得出△OAB是等边三角形,为后继求解打好基础.
19.B
【分析】作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,首先利用勾股定理求得OM的长,然后判定四边形OMPN是正方形,求得正方形的对角线的长即可求得OP的长.
【详解】作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,
∵AB=CD=16,
∴BM=DN=8,
∴OM=ON==6,
∵AB⊥CD,
∴∠DPB=90°,
∵OM⊥AB于M,ON⊥CD于N,
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形,
∵OM=ON,
∴四边形MONP是正方形,
∴OP=.
故选B.
【点睛】本题考查的是垂径定理,正方形的判定与性质及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
20.D
【分析】由切线长定理可得PA=PB, CA=CE,DE=DB, 由于△PCD的周长=PC+CE+ED+PD, 所以△PCD的周=PC+CA+BD+PD=PA+PB=2PA, 故可求得三角形的周长.
【详解】解:PA、PB为圆的两条相交切线,
PA=PB,
同理可得: CA=CE, DE=DB.
△PCD的周长=PC+CE+ED+PD,
△PCD的周长=PC+CA+BD+PD=PA+PB=2PA,
△PCD的周长=10,
故选D
【点睛】本题考查了切线的性质以及切线长定理的运用.
21.B
【分析】根据切线长定理进行求解即可.
【详解】解:∵△ABC的内切圆⊙O与AB,BC,CA分别相切于点D,E,F,
∴AF=AD=2,BD=BE,CE=CF,
∵BE+CE=BC=5,
∴BD+CF=BC=5,
∴△ABC的周长=2+2+5+5=14,
故选B.
【点睛】本题考查了三角形的内切圆以及切线长定理,熟练掌握切线长定理是解题的关键.
22.A
【分析】先画出图形,分别求出扇形和圆的半径,再根据面积公式求出面积,最后求出比值即可.
【详解】如图1,连接OD,
∵四边形ABCD是正方形,
∴∠DCB=∠ABO=,AB=BC=CD=1,
∵∠AOB=,
∴OB=AB=1,
由勾股定理得:OD=,
∴扇形的面积是;
如图2,连接MB、MC,
∵四边形ABCD是⊙M的内接四边形,四边形ABCD是正方形,
∴∠BMC=,MB=MC,
∴∠MCB=∠MBC=,
∵BC=1,
∴MC=MB=,
∴⊙M的面积是,
∴扇形和圆形纸板的面积比是,
故选:A.
【点睛】本题考察圆内接四边形的性质、正方形的性质、扇形的面积公式,求出扇形和圆的面积是解题的关键.
23.A
【详解】∵直线l:y=kx+4与x轴、y轴分别交于A、B,
∴B(0,4),
∴OB=4,
在RT△AOB中,∠OAB=30°,
∴OA=OB=×4=12,
∵⊙P与l相切,设切点为M,连接PM,则PM⊥AB,
∴PM=PA,
设P(x,0),
∴PA=12-x,
∴⊙P的半径PM=PA=6-x,
∵x为整数,PM为整数,
∴x可以取0,2,4,6,8,10,6个数,
∴使得⊙P成为整圆的点P个数是6.
故选A.
【点睛】考点:1.切线的性质;2.一次函数图象上点的坐标特征.
24.A
【分析】过O作OECD于点E,根据AB是⊙O的切线,得出∠ABO=90°,求出即可.
【详解】如图,过O作OECD于点E,
AB是⊙O的切线,
∠ABO=90°,
∠A=30°,
∠AOB=60°,
∠COD=120°,
OC=OD=2,
,
OE=1,CD=2DE=,
.
故选A.
【点睛】本题考查扇形的面积,三角形的面积,阴影部分的面积,掌握扇形的面积,三角形的面积,阴影部分的面积世界关键.
25.5
【详解】∵多边形的每个外角都等于72°,
∵多边形的外角和为360°,
∴360°÷72°=5,
∴这个多边形的边数为5.
故答案为5.
26.3或1
【分析】根据垂径定理推论,得AO⊥BC,由勾股定理得OD=1,分两种情况分别求出AD的值,即可
【详解】如图所示:∵⊙O的半径为2,弦BC=2,点A是⊙O上一点,且AB=AC,
∴,
∴AO⊥BC,
∴BD=BC=,
在Rt△OBD中,
∵BD2+OD2=OB2,即()2+OD2=22,解得OD=1,
∴当如图1所示时,AD=OA﹣OD=2﹣1=1;
当如图2所示时,AD=OA+OD=2+1=3.
故答案为1或3.
【点睛】本题主要考查垂径定理和勾股定理,掌握垂径定理和勾股定理是解题的关键.
27.(3,2).
【分析】过点P作PD⊥x轴于点D,连接OP,先由垂径定理求出OD的长,再根据勾股定理求出PD的长,故可得出答案.
【详解】过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,
∴OD=OA=3,
在Rt△OPD中 ∵OP= OD=3,
∴PD=2
∴P(3,2) .
故答案为(3,2).
【点睛】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
28.30°
【分析】根据点的坐标得到OD,OC的长度,利用勾股定理求出CD的长度,由此求出∠OCD的度数;由于∠OBD和∠OCD是弧OD所对的圆周角,根据“同弧所对的圆周角相等”求出∠OBD的度数.
【详解】连接CD.
由题意得∠COD=90°,
∴CD是⊙A的直径.
∵D(0,1),C(,0),
∴OD=1,OC=,
∴CD==2,
∴∠OCD=30°,
∴∠OBD=∠OCD=30°.(同弧或等弧所对的圆周角相等)
故答案为30°.
【点睛】本题考查圆周角定理以及推论,可以结合圆周角进行解答.
29.
【分析】先由勾股定理求出AB的长,再根据切线性质和正方形的判定这证得四边形OECF是正方形,然后利用切线长定理求得半径r即可.
【详解】如图,
∵在,,,
∴由勾股定理得:,
∵圆O为的内切圆,
∴,;
四边形是正方形;
由切线长定理,得:,,;
,
即:,
故答案为:2.
【点睛】本题考查了切线的性质、正方形的判定与性质、切线长定理、勾股定理,熟练掌握切线性质和切线长定理是解答的关键.
30.πa
【分析】首先根据等边三角形的性质得出∠A=∠B=∠C=60°,AB=BC=CA=a,再利用弧长公式求出的长=的长=的长=,那么勒洛三角形的周长为
【详解】解:如图.∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=CA=a,
∴的长=的长=的长=,
∴勒洛三角形的周长为
故答案为:πa.
【点睛】本题考查了弧长公式,解题的关键是掌握(弧长为l,圆心角度数为n,圆的半径为R),也考查了等边三角形的性质.
31. .
【分析】当PC⊥AB时,线段PQ最短;连接CP、CQ,根据勾股定理知PQ2=CP2﹣CQ2,先求出CP的长,然后由勾股定理即可求得答案.
【详解】连接CP、CQ;如图所示:
∵PQ是⊙C的切线,∴CQ⊥PQ,∠CQP=90°,根据勾股定理得:PQ2=CP2﹣CQ2,∴当PC⊥AB时,线段PQ最短.
∵在Rt△ACB中,∠A=30°,BC=2,∴AB=2BC=4,AC=2,∴CP===,∴PQ==,∴PQ的最小值是.
故答案为.
【点睛】本题考查了切线的性质以及勾股定理的运用;注意掌握辅助线的作法,注意当PC⊥AB时,线段PQ最短是关键.
32.18
【分析】由中知要使取得最小值,则需取得最小值,连接,交于点,当点位于位置时,取得最小值,据此求解可得.
【详解】解:连接,
,
,
,
,
若要使取得最小值,则需取得最小值,
连接,交于点,当点位于位置时,取得最小值,
过点作轴于点,
则,,
,
又,
,
,
故答案是:18.
【点睛】本题主要考查点与圆的位置关系,解题的关键是根据直角三角形斜边上的中线等于斜边的一半得出AB取得最小值时点P的位置.
33.(1)见解析;(2)3
【分析】(1)连接OD,根据已知条件得到∠BOD=180°=60°,根据等腰三角形的性质得到∠ADO=∠DAB=30°,得到∠EDA=60°,求得OD⊥DE,于是得到结论;
(2)连接BD,根据圆周角定理得到∠ADB=90°,解直角三角形即可得到结论.
【详解】(1)证明:连接OD,
∵,
∴∠BOD=180°=60°,
∵,
∴∠EAD=∠DAB=BOD=30°,
∵OA=OD,
∴∠ADO=∠DAB=30°,
∵DE⊥AC,
∴∠E=90°,
∴∠EAD+∠EDA=90°,
∴∠EDA=60°,
∴∠EDO=∠EDA+∠ADO=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:连接BD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠DAB=30°,AB=6,
∴BD=AB=3,
∴AD==3.
【点睛】本题考查了切线的证明,及线段长度的计算,熟知圆的性质及切线的证明方法,以及含30°角的直角三角形的特点是解题的关键.
34.(1)见解析;(2)AD=.
【分析】(1)连接FO,可根据三角形中位线的性质可判断易证OF∥AB,然后根据直径所对的圆周角是直角,可得CE⊥AE,进而知OF⊥CE,然后根据垂径定理可得∠FEC=∠FCE,∠OEC=∠OCE,再通过Rt△ABC可知∠OEC+∠FEC=90°,因此可证FE为⊙O的切线;
(2)在Rt△OCD中和Rt△ACD中,分别利用勾股定理分别求出CD,AD的长即可 .
【详解】
(1)证明:连接CE,如图所示:
∵AC为⊙O的直径,
∴∠AEC=90°.
∴∠BEC=90°,
∵点F为BC的中点,
∴EF=BF=CF,
∴∠FEC=∠FCE,
∵OE=OC,
∴∠OEC=∠OCE,
∵∠FCE+∠OCE=∠ACB=90°,
∴∠FEC+∠OEC=∠OEF=90°,
∴EF是⊙O的切线.
(2)解:∵OA=OE,∠EAC=60°,
∴△AOE是等边三角形.
∴∠AOE=60°,
∴∠COD=∠AOE=60°,
∵⊙O的半径为2,
∴OA=OC=2
在Rt△OCD中,∵∠OCD=90°,∠COD=60°,
∴∠ODC=30°,
∴OD=2OC=4,
∴CD=.
在Rt△ACD中,∵∠ACD=90°,AC=4,CD=.
∴AD==.
【点睛】本题主要考查直角三角形、全等三角形的判定与性质以及与圆有关的位置关系 .
35.(1)见解析;(2)
【分析】(1)根据,可得,根据对顶角相等可得,进而可得,根据,可得,结合,根据角度的转化可得,进而即可证明是的切线;
(2)根据,可得,设,则,分别求得,进而根据勾股定理列出方程解方程可得,进而根据即可求得.
【详解】(1),
,
,
,
,
,
是直径,
,
,
是的切线;
(2),
,
,
设,则,
,,
在中,,
即,
解得(舍去),
.
【点睛】本题考查了切线的判定,勾股定理解直角三角形,正切的定义,利用角度相等则正切值相等将已知条件转化是解题的关键.
36.(1)证明见解析;(2)证明见解析;
【分析】(1)连接AD,根据中垂线定理不难求得AB=AC;
(2)要证DE为⊙O的切线,只要证明∠ODE=90°即可.
【详解】(1)连接AD;
∵AB是⊙O的直径,
∴∠ADB=90°.
又∵DC=BD,
∴AD是BC的中垂线.
∴AB=AC.
(2)连接OD;
∵OA=OB,CD=BD,
∴OD∥AC.
∴∠ODE=∠CED.
又∵DE⊥AC,
∴∠CED=90°.
∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
【点睛】考点:切线的判定
37.(1)证明见解析 (2)﹣6π
【分析】(1)直接利用切线的判定方法结合圆心角定理分析得出OD⊥EF,即可得出答案;
(2)直接利用条件得出S△ACD=S△COD,再利用S阴影=S△AED﹣S扇形COD求出答案.
【详解】(1)证明:连接OD,
∵D为弧BC的中点,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∵DE⊥AC,
∴∠E=90°,
∴∠CAD+∠EDA=90°,即∠ADO+∠EDA=90°,
∴OD⊥EF,
∴EF为半圆O的切线;
(2)解:连接OC与CD,
∵DA=DF,
∴∠BAD=∠F,
∴∠BAD=∠F=∠CAD,
又∵∠BAD+∠CAD+∠F=90°,
∴∠F=30°,∠BAC=60°,
∵OC=OA,
∴△AOC为等边三角形,
∴∠AOC=60°,∠COB=120°,
∵OD⊥EF,∠F=30°,
∴∠DOF=60°,
在Rt△ODF中,DF=6,
∴OD=DF tan30°=6,
在Rt△AED中,DA=6,∠CAD=30°,
∴DE=DA sin30°=3,EA=DA cos30°=9,
∵∠COD=180°﹣∠AOC﹣∠DOF=60°,
由CO=DO,
∴△COD是等边三角形,
∴∠OCD=60°,
∴∠DCO=∠AOC=60°,
∴CD∥AB,
故S△ACD=S△COD,
∴S阴影=S△AED﹣S扇形COD==.
【点睛】此题主要考查了切线的判定,圆周角定理,等边三角形的判定与性质,解直角三角形及扇形面积求法等知识,得出S△ACD=S△COD是解题关键.
38.(1)证明见解析;(2)
【详解】分析:(1)根据平行线的性质得出∠AEO=90°,再利用垂径定理证明即可;
(2)根据弧长公式解答即可.
详证明:(1)∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,
即OC⊥AD,
∴AE=ED;
(2)∵OC⊥AD,
∴ ,
∴∠ABC=∠CBD=36°,
∴∠AOC=2∠ABC=2×36°=72°,
∴ =.
点睛:此题考查弧长公式,关键是根据弧长公式和垂径定理解答.
39.(1) B(,2).(2)证明见解析.
【分析】(1)在Rt△ABN中,求出AN、AB即可解决问题;
(2)连接MC,NC.只要证明∠MCD=90°即可
【详解】(1)∵A的坐标为(0,6),N(0,2),
∴AN=4,
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8,
∴由勾股定理可知:NB=,
∴B(,2).
(2)连接MC,NC
∵AN是⊙M的直径,
∴∠ACN=90°,
∴∠NCB=90°,
在Rt△NCB中,D为NB的中点,
∴CD=NB=ND,
∴∠CND=∠NCD,
∵MC=MN,
∴∠MCN=∠MNC,
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°,
即MC⊥CD.
∴直线CD是⊙M的切线.
考点:切线的判定;坐标与图形性质.
40.(1)证明见解析;(2)
【分析】(1)连接OA、OD,如图,根据垂径定理的推理,由D为BE的下半圆弧的中点得到OD⊥BE,则∠D+∠DFO=90°,再由AC=FC得到∠CAF=∠CFA,根据对顶角相等得∠CFA=∠DFO,所以∠CAF=∠DFO,加上∠OAD=∠ODF,则∠OAD+∠CAF=90°,于是根据切线的判定定理即可得到AC是⊙O的切线;
(2)由于圆的半径R=5,EF=3,则OF=2,然后在Rt△ODF中利用勾股定理计算DF的长.
【详解】解:(1)连接OA、OD,如图,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,
∴∠D+∠DFO=90°,
∵AC=FC,
∴∠CAF=∠CFA,
∵∠CFA=∠DFO,
∴∠CAF=∠DFO,
而OA=OD,
∴∠OAD=∠ODF,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)∵圆的半径R=5,EF=3,
∴OF=2,
在Rt△ODF中,∵OD=5,OF=2,
∴DF=.
【点睛】本题考查切线的判定,垂径定理,勾股定理解直角三角形,解题的关键是作出辅助线.
41.(1)证明见解析;(2)6.
【详解】试题分析:(1)连接OD、CD,由AC为⊙O的直径知△BCD是直角三角形,结合E为BC的中点知∠CDE=∠DCE,由∠ODC=∠OCD且∠OCD+∠DCE=90°可得答案;
(2)设⊙O的半径为r,由OD2+DF2=OF2,即r2+42=(r+2)2可得r=3,即可得出答案.
试题解析:(1)如图,连接OD、CD.∵AC为⊙O的直径,∴△BCD是直角三角形,∵E为BC的中点,∴BE=CE=DE,∴∠CDE=∠DCE,∵OD=OC,∴∠ODC=∠OCD,∵∠ACB=90°,∴∠OCD+∠DCE=90°,∴∠ODC+∠CDE=90°,即OD⊥DE,∴DE是⊙O的切线;
(2)设⊙O的半径为r,∵∠ODF=90°,∴OD2+DF2=OF2,即r2+42=(r+2)2,解得:r=3,∴⊙O的直径为6.
考点:切线的判定与性质.
42.(1)见解析;(2)2
【分析】(1)利用圆周角定理得到.则,根据平行线的判定得,然后根据平行线的性质得,最后根据切线的判定定理可得到结论;
(2)连接,如图,根据垂径定理得到,然后利用勾股定理觉得即可.
【详解】(1)证明:,
而.
,
,
,
,
直线是的切线;
(2)解:连接,如图,
,
,
在中,,
即的半径为2.
【点睛】本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了圆周角定理和垂径定理.解题关键是综合运用定理进行推理的能力,题目比较典型,是一道综合性比较强的题目.
43.(1)证明见解析;(2)
【详解】分析:(1)要证明是圆的切线,须证明过切点的半径垂直,所以连接OB,证明OB⊥PE即可.
(2)要求sinE,首先应找出∠E所在的直角三角形,然后利用直角三角函数求解即可.而sinE既可放在直角三角形EAP中,也可放在直角三角形EBO中,所以利用相似三角形的性质求出EP或EO的长即可解决问题
详解:(1)证明:连接OB
∵PO⊥AB,
∴AC=BC,
∴PA=PB,
在△PAO和△PBO中
,
∴△PAO和≌△PBO,
∴∠OBP=∠OAP=90°,
∴PB是⊙O的切线.
(2)连接BD,则BD∥PO,且BD=2OC=6
在Rt△ACO中,OC=3,AC=4
∴AO=5
在Rt△ACO与Rt△PAO中,
∠APO=∠APO,
∠PAO=∠ACO=90°
∴△ACO △PAO
∴
∴PO=,PA=
∴PB=PA=
在△EPO与△EBD中,
BD∥PO
∴△EPO∽△EBD
∴,
解得EB=,PE=,
∴sinE=.
点睛:本题考查了切线的判定以及相似三角形的判定和性质.能够通过作辅助线将所求的角转移到相应的直角三角形中,是解答此题的关键.
44.(1)证明见解析(2)
【分析】(1)连结OC,如图,由AD平分∠EAC得到∠1=∠3,加上∠1=∠2,则∠3=∠2,于是可判断OD∥AE,根据平行线的性质得OD⊥CE,然后根据切线的判定定理得到结论;
(2)由△CDB∽△CAD,可得,推出CD2=CB CA,可得(3)2=3CA,推出CA=6,推出AB=CA﹣BC=3,,设BD=k,AD=2k,在Rt△ADB中,可得2k2+4k2=5,求出k即可解决问题.
【详解】(1)证明:连结OC,如图,
∵AD平分∠EAC,
∴∠1=∠3,
∵OA=OD,
∴∠1=∠2,
∴∠3=∠2,
∴OD∥AE,
∵AE⊥DC,
∴OD⊥CE,
∴CE是⊙O的切线;
(2)∵∠CDO=∠ADB=90°,
∴∠2=∠CDB=∠1,∵∠C=∠C,
∴△CDB∽△CAD,
∴,
∴CD2=CB CA,
∴(3)2=3CA,
∴CA=6,
∴AB=CA﹣BC=3,,设BD=k,AD=2k,
在Rt△ADB中,2k2+4k2=5,
∴k=,
∴AD=.
45.(1)证明见解析;(2).
【分析】(1)连接OC,由OA=OC可以得到∠OAC=∠OCA,然后利用角平分线的性质可以证明∠DAC=∠OCA,接着利用平行线的判定即可得到OC∥AD,然后就得到OC⊥CD,由此即可证明直线CD与⊙O相切于C点;
(2)连接BC,∠BAC=30°,在Rt△ABC中可求得AC,同理在Rt△ACD中求得CD.
【详解】(1)证明:连接CO,
∵AO=CO,
∴∠OAC=∠OCA,
∵AC平分∠DAB,
∴∠OAC=∠DAC,
∴∠DAC=∠OCA,
∴CO∥AD,
∴CO⊥CD,
∴DC为⊙O的切线;
(2)解:连接BC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠DAB=60°,AC平分∠DAB,
∴∠BAC=∠DAB=30°,
∵⊙O的半径为3,
∴AB=6,
∴AC=AB=3.
∵∠CAD=30°
∴
【点睛】此题主要考查了切线的性质与判定,解题时首先利用切线的判定证明切线,然后利用含特殊角度的直角三角形求得边长即可解决问题.
46.(1)证明见解析;(2);
【分析】(1)连接OC,根据CD为切线可得OC⊥CD,再根据平行线的性质即可得出结论;
(2)连接AE交OC于G,根据圆与平行线的性质易得四边形CDEG为矩形,再根据勾股定理即可得出结论.
【详解】(1)证明:连接OC,如图,
∵CD为切线,
∴OC⊥CD,
∵BD⊥DF,
∴OC∥BD,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2,
∴∠2=∠3,
∴BC平分∠ABD;
(2)解:连接AE交OC于G,如图,
∵AB为直径,
∴∠AEB=90°,
∵OC⊥CD,ED⊥CD,
∴四边形CDEG为矩形,
∴GE=CD=8,
∵OC∥BD,
∴,
∴AE=2EG=16,
在Rt△ABE中,AB==4,
即圆的直径为4.
【点睛】本题考查了勾股定理、切线与平行线的性质,矩形的性质与判定,平行线分线段成比例定理,解题的关键是熟练的掌握勾股定理、切线与平行线的性质.
47.(1)证明见解析;(2)DE与⊙O相切;(3)
【分析】(1)连接AD,根据等腰三角形三线合一性质得到AD⊥BC,再根据90°的圆周角所对的弦为直径即可证得AB是⊙O的直径;
(2)DE与圆O相切,理由为:连接OD,利用中位线定理得到OD∥AC,利用两直线平行内错角相等得到∠ODE为直角,再由OD为半径,即可得证;
(3)由AB=AC,且∠BAC=60°,得到DABC为等边三角形,连接BF,DE为DCBF中位线,求出BF的长,即可确定出DE的长.
【详解】解:(1)证明:连接AD,
∵AB=AC,BD=DC,
∴AD⊥BC,
∴∠ADB=90°,
∴AB为⊙O的直径;
(2)DE与⊙O相切,
理由为:连接OD,
∵O、D分别为AB、BC的中点,
∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∵OD为⊙O的半径,
∴DE与⊙O相切;
(3)解:连接BF,
∵AB=AC,∠BAC=60°,
∴△ABC为等边三角形,
∴AB=AC=BC=6,
∵AB为⊙O的直径,
∴∠AFB=∠DEC=90°,
∴AF=CF=3,DE∥BF,
∵D为BC中点,
∴E为CF中点,DE=BF,
在Rt△ABF中,∠AFB=90°,AB=6,AF=3,
∴BF=,则DE=BF=.
48.(1)见解析;(2)4.5
【分析】(1)作OF⊥AC于F,利用角平分线的性质证明OF=OB,即可证明AC是⊙O的切线.
(2)利用圆周角定理证明△CBE∽△CDB,根据相似三角形的性质即可求解.
【详解】(1)证明:作OF⊥AC于F,
∵⊙O与BC相切于点B,∴OB⊥BC,
∵CO平分∠ACB,
∴OF=OB ,
又OB是半径,OF⊥AC于F,
∴AC是⊙O的切线.
(2)解:∵DE是直径,
∴∠DBE=90°,
又tan∠BDE,∴,
由(1),知∵OE=OB,OB⊥BC ,
∴∠OBC=90° ,
∴∠DBC=∠OBE,
∴∠E=∠OBE,
∴∠E=∠DBC,
又 ∠C=∠C,
∴△CBE∽△CDB,
∴,
∵BC=6,
∴,
∴,
∴DE=9,
∵OD=4.5,即⊙O的半径是4.5.
【点睛】本题考查了切线的判定和性质,相似三角形的判定和性质,正切函数,注意掌握辅助线的作法,注意数形结合思想的应用.
