【新课标】7.2.2定义与命题 课件(共26张PPT)
文档属性
| 名称 | 【新课标】7.2.2定义与命题 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 15:08:34 | ||
图片预览








文档简介
(共26张PPT)
7.2.2定义与命题
北师大版八年级上册
教学目标
1.了解命题中的真命题、假命题、定理的含义;
2.解命题的构成,能区分命题中的条件和结论。
3.经历实际情境,初步体会公理化思想和方法,了解本教材所采用的公理.
复习导入
1.什么是定义?
对名称和术语的含义加以描述,作出明确规定.也就是给出它们的定义.
2.什么是命题?
判断一件事情的句子,叫做命题.
3.命题由_______和_______两部分组成.可以写成“______________ ”的形式.
条件
结论
如果……那么……
新知讲解
正确的命题是真命题,不正确的命题是假命题.
想一想:
要说明一个命题是假命题,只需举一个反例,那么如何证实一个命题是真命题呢?
新知讲解
用我们以前学过的观察、实验、验证特例等方法.
这些方法往往不可靠.
能不能根据已经知道的真命题证实呢?
那已经知道的真命题又是如何证实的?
哦……那可怎么办?
新知讲解
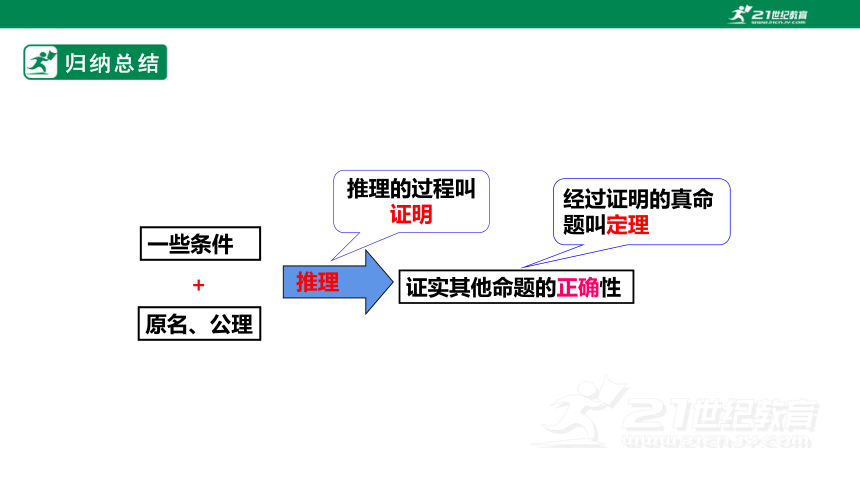
在数学发展史上,数学家们也遇到过类似的问题。公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得(公元前300前后)编写了一本书,书名叫《原本》,为了说明每一结论的正确性,他在编写这本书时进行了大胆创新,挑选了一部分数学名词和一部分公认的真命题作为证实其他命题的起始依据,其中的数学名词称为原名,公认的真命题称为公理,除了公理外,其他命题的正确性都通过推理的方法证实,推理的过程称为证明,经过证明的真命题称为定理,而证明所需要的定义、公理和其他定理都编写在要证明的这个定理的前面。《原本》问世之前,世界上还没有一本数学书籍像《原本》这样编排,因此,《原本》是一部具有划时代意义的著作。
归纳总结
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
原名、公理
一些条件
+
归纳总结
本套教科书选用九条基本事实作为证明的出发点和依据,我们已经认识了其中的八条,它们是:
(1)两点确定一条直线.
(2)两点之间线段最短.
(3)同一平面内,过一点有且只有一条直线与已知直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 (简述为:同位角相等,两直线平行).
(5)过直线外一点有且只有一条直线与这条直线平行.
(6)两边及其夹角分别相等的两个三角形全等.
想一想
(7)两角及其夹边分别相等的两个三角形全等.
(8)三边分别相等的两个三角形全等.
另外一条基本事实我们将在后面的学习中认识它.此外,数与式的运算律和运算法则、等式的有关性质,以及反映大小关系的有关性质都可以作为证明的依据. 例如,如果a=b,b=c, 那么a=c,这一性质也可以作为证明的依据,称为“等量代换”.又如,如果a>b,b>c, 那么a>c,这一性质同样可以作为证明的依据.
新知讲解
证明下面的定理:
1.同角(等角)的补角相等.
2.同角(等角)的余角相等.
3.三角形的任意两边之和大于第三边
根据以上基本事实,我们可以证明已经探索过的结论.
新知讲解
1.1 已知:∠A=∠B,∠C和∠D分别是∠A、∠B的补角.
求证:∠C=∠D
证明:∵ ∠C和∠D分别是∠A、∠B的补角.
∴∠C=180°-∠A,∠D=180°-∠B.
∵∠A=∠B(已知).
∴∠C=∠D(等量代换).
∴等角的补角相等.
想一想
1.2 已知:∠B和∠C是∠A的补角,
求证:∠B=∠C
证明:∵ ∠B和∠C是∠A的补角,
∴∠B=180°-∠A,∠C=180°-∠A.
∴∠B=∠C(等量代换).
∴同角的补角相等.
想一想
2.1 已知:∠B和∠C是∠A的余角,
求证:∠B=∠C
证明:∵ ∠B和∠C是∠A的余角,
∴∠B=90°-∠A,∠C=90°-∠A.
∴∠B=∠C(等量代换).
∴同角的余角相等.
新知讲解
2.2 已知:∠A=∠B,∠C和∠D分别是∠A、∠B的余角.
求证:∠C=∠D
证明:∵ ∠C和∠D分别是∠A、∠B的余角.
∴∠C=90°-∠A,∠D=90°-∠B.
∵∠A=∠B(已知).
∴∠C=∠D(等量代换).
∴等角的余角相等.
新知讲解
3.已知:AB,AC是△ABC的两边
求证:AB+AC>BC
证明:∵BC是点B到点C的距离,
AB+AC是连接点B、点C的一条曲线长度。
根据两点之间线段最短得:AB+AC>BC
典例精析
例 已知:如图,直线AB与直线CD相交于点O,∠AOC 与∠BOD是对顶角.
求证: ∠AOC =∠BOD
证明:∵直线AB与直线CD相交于点О,
∴∠AOB和∠COD都是平角(平角的定义)
∴∠AOC和∠BOD都是∠AOD的补角(补角的定义).
∴∠AOC=∠BOD(同角的补角相等).
由上面的例题,我们可以得到定理:
定理 对顶角相等.
归纳总结
证明过程的注意事项:
证明的每一步推理都要有根据,不能“想当然”.这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理等.
证明的一般步骤:
1.已知:写出命题的条件(必要时结合图形).
2.求证:写出命题的结论.
3.证明:写出演绎推理的过程.
课堂练习
1.“两点之间,线段最短”这个语句是( )
A.定理 B.公理 C.定义 D.只是命题
2.“同一平面内,不相交的两条直线叫做平行线”这个语句是( )
A.定理 B.公理 C.定义 D.只是命题
B
C
课堂练习
3.(1)定理是真命题(填“真”或“假”,下同).
“如果ab=0,那么a=0”是_____________.
“如果a=0,那么ab=0” 是_____________.
(2)“如果(a-1)(a-2)=0,那么a=2”是假命题,反例是_____________.
假命题
真命题
a=1
课堂练习
4.判断下列命题是真命题还是假命题,如果是假命题,请举出一个反例.
(1)如果一个数是偶数,那么这个数是4的倍数.
(2)两个负数的差一定是负数.
解:(1)假命题.反例:6是偶数,但6不是4的倍数.
(2)假命题.反例:(-5)-(-8)=+3.
课堂练习
5.如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1= ,∠2= .
(2)请观察∠1,∠2与∠ABC分别有怎样的关系,请你由此归纳一个真命题.
25°
155°
解:(2)∠1=∠ABC,∠2+∠ABC=180°.
真命题:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
课堂总结
命题
真命题
假命题(举反例)
公理(公认的真命题)
定理(经过证明的真命题)
其他不常用的真命题(推理)
证明:推理的过程
板书设计
7.2.2定义与命题
证明的一般步骤:
①审题,分清命题的条件和结论;
②画图,结合图形写出已知和求证;
③分析因果关系,找出证明途径;
④有条理地写出证明过程.
作业布置
教材171页习题第1,2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
7.2.2定义与命题
北师大版八年级上册
教学目标
1.了解命题中的真命题、假命题、定理的含义;
2.解命题的构成,能区分命题中的条件和结论。
3.经历实际情境,初步体会公理化思想和方法,了解本教材所采用的公理.
复习导入
1.什么是定义?
对名称和术语的含义加以描述,作出明确规定.也就是给出它们的定义.
2.什么是命题?
判断一件事情的句子,叫做命题.
3.命题由_______和_______两部分组成.可以写成“______________ ”的形式.
条件
结论
如果……那么……
新知讲解
正确的命题是真命题,不正确的命题是假命题.
想一想:
要说明一个命题是假命题,只需举一个反例,那么如何证实一个命题是真命题呢?
新知讲解
用我们以前学过的观察、实验、验证特例等方法.
这些方法往往不可靠.
能不能根据已经知道的真命题证实呢?
那已经知道的真命题又是如何证实的?
哦……那可怎么办?
新知讲解
在数学发展史上,数学家们也遇到过类似的问题。公元前3世纪,人们已经积累了大量的数学知识,在此基础上,古希腊数学家欧几里得(公元前300前后)编写了一本书,书名叫《原本》,为了说明每一结论的正确性,他在编写这本书时进行了大胆创新,挑选了一部分数学名词和一部分公认的真命题作为证实其他命题的起始依据,其中的数学名词称为原名,公认的真命题称为公理,除了公理外,其他命题的正确性都通过推理的方法证实,推理的过程称为证明,经过证明的真命题称为定理,而证明所需要的定义、公理和其他定理都编写在要证明的这个定理的前面。《原本》问世之前,世界上还没有一本数学书籍像《原本》这样编排,因此,《原本》是一部具有划时代意义的著作。
归纳总结
证实其他命题的正确性
推理
推理的过程叫证明
经过证明的真命题叫定理
原名、公理
一些条件
+
归纳总结
本套教科书选用九条基本事实作为证明的出发点和依据,我们已经认识了其中的八条,它们是:
(1)两点确定一条直线.
(2)两点之间线段最短.
(3)同一平面内,过一点有且只有一条直线与已知直线垂直.
(4)两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 (简述为:同位角相等,两直线平行).
(5)过直线外一点有且只有一条直线与这条直线平行.
(6)两边及其夹角分别相等的两个三角形全等.
想一想
(7)两角及其夹边分别相等的两个三角形全等.
(8)三边分别相等的两个三角形全等.
另外一条基本事实我们将在后面的学习中认识它.此外,数与式的运算律和运算法则、等式的有关性质,以及反映大小关系的有关性质都可以作为证明的依据. 例如,如果a=b,b=c, 那么a=c,这一性质也可以作为证明的依据,称为“等量代换”.又如,如果a>b,b>c, 那么a>c,这一性质同样可以作为证明的依据.
新知讲解
证明下面的定理:
1.同角(等角)的补角相等.
2.同角(等角)的余角相等.
3.三角形的任意两边之和大于第三边
根据以上基本事实,我们可以证明已经探索过的结论.
新知讲解
1.1 已知:∠A=∠B,∠C和∠D分别是∠A、∠B的补角.
求证:∠C=∠D
证明:∵ ∠C和∠D分别是∠A、∠B的补角.
∴∠C=180°-∠A,∠D=180°-∠B.
∵∠A=∠B(已知).
∴∠C=∠D(等量代换).
∴等角的补角相等.
想一想
1.2 已知:∠B和∠C是∠A的补角,
求证:∠B=∠C
证明:∵ ∠B和∠C是∠A的补角,
∴∠B=180°-∠A,∠C=180°-∠A.
∴∠B=∠C(等量代换).
∴同角的补角相等.
想一想
2.1 已知:∠B和∠C是∠A的余角,
求证:∠B=∠C
证明:∵ ∠B和∠C是∠A的余角,
∴∠B=90°-∠A,∠C=90°-∠A.
∴∠B=∠C(等量代换).
∴同角的余角相等.
新知讲解
2.2 已知:∠A=∠B,∠C和∠D分别是∠A、∠B的余角.
求证:∠C=∠D
证明:∵ ∠C和∠D分别是∠A、∠B的余角.
∴∠C=90°-∠A,∠D=90°-∠B.
∵∠A=∠B(已知).
∴∠C=∠D(等量代换).
∴等角的余角相等.
新知讲解
3.已知:AB,AC是△ABC的两边
求证:AB+AC>BC
证明:∵BC是点B到点C的距离,
AB+AC是连接点B、点C的一条曲线长度。
根据两点之间线段最短得:AB+AC>BC
典例精析
例 已知:如图,直线AB与直线CD相交于点O,∠AOC 与∠BOD是对顶角.
求证: ∠AOC =∠BOD
证明:∵直线AB与直线CD相交于点О,
∴∠AOB和∠COD都是平角(平角的定义)
∴∠AOC和∠BOD都是∠AOD的补角(补角的定义).
∴∠AOC=∠BOD(同角的补角相等).
由上面的例题,我们可以得到定理:
定理 对顶角相等.
归纳总结
证明过程的注意事项:
证明的每一步推理都要有根据,不能“想当然”.这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理等.
证明的一般步骤:
1.已知:写出命题的条件(必要时结合图形).
2.求证:写出命题的结论.
3.证明:写出演绎推理的过程.
课堂练习
1.“两点之间,线段最短”这个语句是( )
A.定理 B.公理 C.定义 D.只是命题
2.“同一平面内,不相交的两条直线叫做平行线”这个语句是( )
A.定理 B.公理 C.定义 D.只是命题
B
C
课堂练习
3.(1)定理是真命题(填“真”或“假”,下同).
“如果ab=0,那么a=0”是_____________.
“如果a=0,那么ab=0” 是_____________.
(2)“如果(a-1)(a-2)=0,那么a=2”是假命题,反例是_____________.
假命题
真命题
a=1
课堂练习
4.判断下列命题是真命题还是假命题,如果是假命题,请举出一个反例.
(1)如果一个数是偶数,那么这个数是4的倍数.
(2)两个负数的差一定是负数.
解:(1)假命题.反例:6是偶数,但6不是4的倍数.
(2)假命题.反例:(-5)-(-8)=+3.
课堂练习
5.如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°.
(1)∠1= ,∠2= .
(2)请观察∠1,∠2与∠ABC分别有怎样的关系,请你由此归纳一个真命题.
25°
155°
解:(2)∠1=∠ABC,∠2+∠ABC=180°.
真命题:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
课堂总结
命题
真命题
假命题(举反例)
公理(公认的真命题)
定理(经过证明的真命题)
其他不常用的真命题(推理)
证明:推理的过程
板书设计
7.2.2定义与命题
证明的一般步骤:
①审题,分清命题的条件和结论;
②画图,结合图形写出已知和求证;
③分析因果关系,找出证明途径;
④有条理地写出证明过程.
作业布置
教材171页习题第1,2题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
