【核心素养目标】7.3平行线的判定 教学设计
文档属性
| 名称 | 【核心素养目标】7.3平行线的判定 教学设计 | 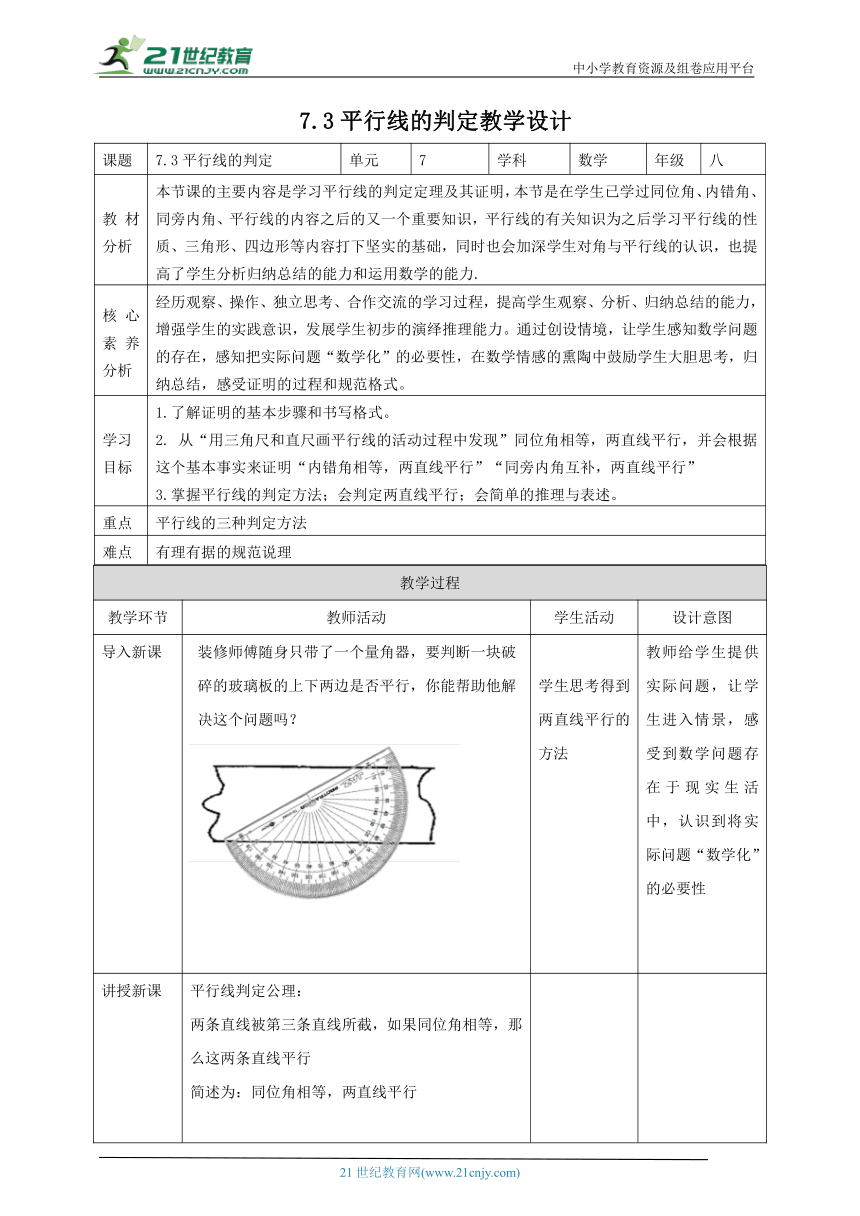 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 15:09:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
7.3平行线的判定教学设计
课题 7.3平行线的判定 单元 7 学科 数学 年级 八
教材分析 本节课的主要内容是学习平行线的判定定理及其证明,本节是在学生已学过同位角、内错角、同旁内角、平行线的内容之后的又一个重要知识,平行线的有关知识为之后学习平行线的性质、三角形、四边形等内容打下坚实的基础,同时也会加深学生对角与平行线的认识,也提高了学生分析归纳总结的能力和运用数学的能力.
核心素养分析 经历观察、操作、独立思考、合作交流的学习过程,提高学生观察、分析、归纳总结的能力,增强学生的实践意识,发展学生初步的演绎推理能力。通过创设情境,让学生感知数学问题的存在,感知把实际问题“数学化”的必要性,在数学情感的熏陶中鼓励学生大胆思考,归纳总结,感受证明的过程和规范格式。
学习 目标 1.了解证明的基本步骤和书写格式。 2. 从“用三角尺和直尺画平行线的活动过程中发现”同位角相等,两直线平行,并会根据这个基本事实来证明“内错角相等,两直线平行”“同旁内角互补,两直线平行” 3.掌握平行线的判定方法;会判定两直线平行;会简单的推理与表述。
重点 平行线的三种判定方法
难点 有理有据的规范说理
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 装修师傅随身只带了一个量角器,要判断一块破碎的玻璃板的上下两边是否平行,你能帮助他解决这个问题吗? 学生思考得到两直线平行的方法 教师给学生提供实际问题,让学生进入情景,感受到数学问题存在于现实生活中,认识到将实际问题“数学化”的必要性
讲授新课 平行线判定公理: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 简述为:同位角相等,两直线平行 几何符号语言: ∵ ∠1=∠2 ∴ a//b 利用基本事实“平行线判定公理” 1. “内错角相等,两直线平行” 2. “同旁内角互补,两直线平行” 已知:如图,∠2和∠3是直线a、b被直线c截出的内错角,且∠2=∠3. 求证:a∥b 证明:∵∠2=∠3(已知),∠1=∠3(对顶角相等), ∴∠1=∠2(等量代换). ∴a//b(同位角相等,两直线平行). 归纳总结: 经过上面的推理过程,证明它是一个真命题,我们把这个真命题称为:直线平行的判定定理. 简单说成:内错角相等,两直线平行. 推理格式: ∵∠3=∠2(已知) ∴a∥b(内错角相等,两直线平行) 证明定理:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。 简述为:同旁内角互补,两直线平行。 条件:同旁内角互补 结论:两直线平行 已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补. 求证:a∥b 证明:∵∠1与∠2互补(已知) ∴∠1+∠2=180°(互补定义) ∴∠1=180°-∠2(等式的性质) ∵∠3+∠2=180°(平角定义) ∴∠3=180°-∠2(等式的性质) ∴∠1=∠3(等量代换) ∴a∥b(同位角相等,两直线平行) 通过上面的推理证明,我们得到直线平行的另一判定定理: 简单说成:同旁内角互补,两直线平行. 推理格式: ∵∠1+∠2=180°(已知) ∴a∥b(同旁内角互补,两直线平行) 想一想: 我们曾经用下图的方法作出了平行线,你能说说其中的道理吗? 解: 如同AB // CD,理由是: ∵ ∠BEF=30°,∠EFC=30° ∴ ∠BEF= ∠EFC. ∴ AB // CD . (内错角相等,两直线平行) 学生思考如何改写,又如何由改写后的文字转化成几何语言的已知求证。 独立思考并完成,然后在小组里交流。 学生通过上述例子,再模仿改写和写已知求证,并用两种方法去证明,让学生感知学习过的知识后立刻运用 学生观看动画,并动手实际操作如何画平行线。 通过改写学生更加清晰定理中的条件和结论,再写出已知和求证,把文字语言转化为几何语言和数学语言,规范学生的书写。 通过自主学习、合作交流、优秀图表展示等环节,既可以锻炼学生的自主学习能力,又发展了学生的合作交流能力、有条理思考的能力和语言表达能力. 通过再次改写和写已知求证,让学生进一步熟悉如何由文字语言转化几何语言的方法,在通过两种方法的证明让学生感知几何证明方法的多样性。 通过动画演示让学生感受“同位角相等,两直线平行”在实际生活中的应用。
课堂练习 对于图中标记的各角,下列条件能够推理得到 a∥b的是( ) A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180° 2.某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.当∠MAC为( )度时,AM与CB平行. A.16 B.60 C.66 D.114 如图,直线a,b被直线c所截, ___________________,则a,b平行. 4.如图,a、b、c三根木棒钉在一起,∠1=70°,∠2=100°,现将木棒a、b同时顺时针旋转一周,速度分别为18度/秒和3度/秒,两根木棒都停止时运动结束,则________ 秒后木棒a,b平行. 5.如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由? 6.如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么? 学生课堂练习,然后上台演示自己的答案。 学以致用,当堂检测及时获知学生对所学知识掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高.
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:7.3平行线的判定 平行的判定方法: 同位角相等,两直线平行 内错角相等,两直线平行 同旁内角互补,两直线平行
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.3平行线的判定教学设计
课题 7.3平行线的判定 单元 7 学科 数学 年级 八
教材分析 本节课的主要内容是学习平行线的判定定理及其证明,本节是在学生已学过同位角、内错角、同旁内角、平行线的内容之后的又一个重要知识,平行线的有关知识为之后学习平行线的性质、三角形、四边形等内容打下坚实的基础,同时也会加深学生对角与平行线的认识,也提高了学生分析归纳总结的能力和运用数学的能力.
核心素养分析 经历观察、操作、独立思考、合作交流的学习过程,提高学生观察、分析、归纳总结的能力,增强学生的实践意识,发展学生初步的演绎推理能力。通过创设情境,让学生感知数学问题的存在,感知把实际问题“数学化”的必要性,在数学情感的熏陶中鼓励学生大胆思考,归纳总结,感受证明的过程和规范格式。
学习 目标 1.了解证明的基本步骤和书写格式。 2. 从“用三角尺和直尺画平行线的活动过程中发现”同位角相等,两直线平行,并会根据这个基本事实来证明“内错角相等,两直线平行”“同旁内角互补,两直线平行” 3.掌握平行线的判定方法;会判定两直线平行;会简单的推理与表述。
重点 平行线的三种判定方法
难点 有理有据的规范说理
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 装修师傅随身只带了一个量角器,要判断一块破碎的玻璃板的上下两边是否平行,你能帮助他解决这个问题吗? 学生思考得到两直线平行的方法 教师给学生提供实际问题,让学生进入情景,感受到数学问题存在于现实生活中,认识到将实际问题“数学化”的必要性
讲授新课 平行线判定公理: 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 简述为:同位角相等,两直线平行 几何符号语言: ∵ ∠1=∠2 ∴ a//b 利用基本事实“平行线判定公理” 1. “内错角相等,两直线平行” 2. “同旁内角互补,两直线平行” 已知:如图,∠2和∠3是直线a、b被直线c截出的内错角,且∠2=∠3. 求证:a∥b 证明:∵∠2=∠3(已知),∠1=∠3(对顶角相等), ∴∠1=∠2(等量代换). ∴a//b(同位角相等,两直线平行). 归纳总结: 经过上面的推理过程,证明它是一个真命题,我们把这个真命题称为:直线平行的判定定理. 简单说成:内错角相等,两直线平行. 推理格式: ∵∠3=∠2(已知) ∴a∥b(内错角相等,两直线平行) 证明定理:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。 简述为:同旁内角互补,两直线平行。 条件:同旁内角互补 结论:两直线平行 已知:如图,∠1和∠2是直线a、b被直线c截出的同旁内角,且∠1与∠2互补. 求证:a∥b 证明:∵∠1与∠2互补(已知) ∴∠1+∠2=180°(互补定义) ∴∠1=180°-∠2(等式的性质) ∵∠3+∠2=180°(平角定义) ∴∠3=180°-∠2(等式的性质) ∴∠1=∠3(等量代换) ∴a∥b(同位角相等,两直线平行) 通过上面的推理证明,我们得到直线平行的另一判定定理: 简单说成:同旁内角互补,两直线平行. 推理格式: ∵∠1+∠2=180°(已知) ∴a∥b(同旁内角互补,两直线平行) 想一想: 我们曾经用下图的方法作出了平行线,你能说说其中的道理吗? 解: 如同AB // CD,理由是: ∵ ∠BEF=30°,∠EFC=30° ∴ ∠BEF= ∠EFC. ∴ AB // CD . (内错角相等,两直线平行) 学生思考如何改写,又如何由改写后的文字转化成几何语言的已知求证。 独立思考并完成,然后在小组里交流。 学生通过上述例子,再模仿改写和写已知求证,并用两种方法去证明,让学生感知学习过的知识后立刻运用 学生观看动画,并动手实际操作如何画平行线。 通过改写学生更加清晰定理中的条件和结论,再写出已知和求证,把文字语言转化为几何语言和数学语言,规范学生的书写。 通过自主学习、合作交流、优秀图表展示等环节,既可以锻炼学生的自主学习能力,又发展了学生的合作交流能力、有条理思考的能力和语言表达能力. 通过再次改写和写已知求证,让学生进一步熟悉如何由文字语言转化几何语言的方法,在通过两种方法的证明让学生感知几何证明方法的多样性。 通过动画演示让学生感受“同位角相等,两直线平行”在实际生活中的应用。
课堂练习 对于图中标记的各角,下列条件能够推理得到 a∥b的是( ) A.∠1=∠2 B.∠2=∠4 C.∠3=∠4 D.∠1+∠4=180° 2.某市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=54°.当∠MAC为( )度时,AM与CB平行. A.16 B.60 C.66 D.114 如图,直线a,b被直线c所截, ___________________,则a,b平行. 4.如图,a、b、c三根木棒钉在一起,∠1=70°,∠2=100°,现将木棒a、b同时顺时针旋转一周,速度分别为18度/秒和3度/秒,两根木棒都停止时运动结束,则________ 秒后木棒a,b平行. 5.如图,已知∠1= ∠3,AC平分∠DAB,你能判断哪两条直线平行?请说明理由? 6.如图,已知∠MCA= ∠ A, ∠ DEC= ∠ B,那么DE∥MN吗?为什么? 学生课堂练习,然后上台演示自己的答案。 学以致用,当堂检测及时获知学生对所学知识掌握情况,并最大限度地调动全体学生学习数学的积极性,使每个学生都能有所收益、有所提高.
课堂小结 通过本节课的学习,你们有什么收获? 学生归纳本节所学内容,并体验核心素养的形成。 训练学生总结归纳能 力;升华知识,拓展知识面,开阔思维。
板书 课题:7.3平行线的判定 平行的判定方法: 同位角相等,两直线平行 内错角相等,两直线平行 同旁内角互补,两直线平行
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
