2022-2023学年高二下学期数学人教A版选修2-31.3.1二项式定理课件(20张PPT)
文档属性
| 名称 | 2022-2023学年高二下学期数学人教A版选修2-31.3.1二项式定理课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 12:34:56 | ||
图片预览







文档简介
(共20张PPT)
1.3.1 二项式定理
创设情境
不积跬步,无以至千里;
不积小流,无以成江海。
———荀子 ·《劝学篇》
释义:做事情不一点一点积累,就永远无法达成目的。
把自己的起始优秀值看成1,假设每天的努力能让自己变得比前一天优秀1%,对优秀值进行复利计算:
第1天努力后优秀值为________________;
第2天努力后优秀值为________________;
......
第30天努力后优秀值为________________;
模型建立
1+0.01
(1+0.01)2
(1+0.01)30
估算(1+0.01)30 的近似值(精确到0.1)
探究新知
艾萨克·牛顿(1643—1727,英国)被誉为人类历史上最伟大的科学家之一,不仅是伟大的物理学家、天文学家,而且还是伟大的数学家。1664年,年仅22岁的牛顿。在数学方面就有了第一项创造性成果,就是发现了二项式定理,又称牛顿二项式定理。
探究新知
②各项中a与b次数之和呈现什么规律
①在以上各展开式中各有多少项
③各项的系数是什么
重点关注
探究新知
在初中,我们用多项式乘法法则得到了(a+b)2 的展开式,如何利用分步乘法计数原理解释上述展开过程?
?
探究
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
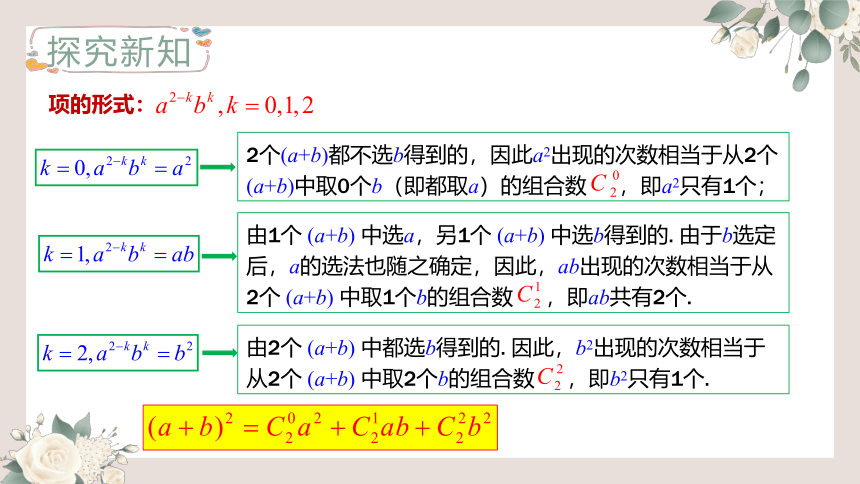
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个 (a+b) 中选a,另1个 (a+b) 中选b得到的. 由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个 (a+b) 中取1个b的组合数 ,即ab共有2个.
由2个 (a+b) 中都选b得到的. 因此,b2出现的次数相当于从2个 (a+b) 中取2个b的组合数 ,即b2只有1个.
探究新知
探究新知
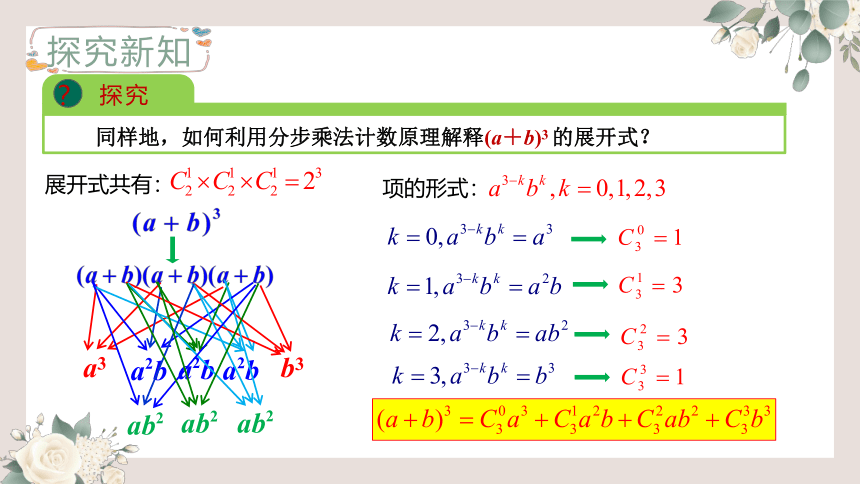
同样地,如何利用分步乘法计数原理解释(a+b)3 的展开式?
?
探究
a3
a2b
a2b
a2b
b3
ab2
ab2
ab2
展开式共有:
项的形式:
探究新知
根据你发现的规律,你能写出(a+b)4 的展开式吗?
?
探究
问题:1).(a+b)4展开后各项形式分别是什么?
2).你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
观察下面式子,你能猜想(a+b)n的展开式吗?
?
探究
概念形成
上述公式叫做二项式定理,右边的多项式叫做 (a+b)n 的二项展开式,其中各项的系数 叫做二项式系数.
式中 的叫做二项展开式的通项,用 表示,即通项为展开式的第 项:
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
概念形成
概念形成
1.在二项式定理中,若设a=1, b=x,则得到公式
2、把b用-b代替
求(1+0.01)30 的近似值(精确到0.1)
结论:我们每天努力1%,30天后,比现在优秀30%
解:
知识探究
例1
求 的展开式.
解:
典例分析
典例分析
例2 (1)求 (1+2x)7 的展开式的第4项;
(2)求 (1+2x)7 的展开式的第4项的系数;
(3)求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
解:
的展开式的通项为
根据题意,得
因此, x2的系数是
求 的展开式中 x2 的系数.
例3
典例分析
解:
的展开式的通项为
求 的展开式常数项的系数.
变式:
典例分析
根据题意,得
解:
求 的展开式中 x3 的系数.
例4:
典例分析
1
x2
x3
x
x3
x3
解:
求 的展开式中 x3y3 的系数.
变式:
典例分析
x
y
x2y3
x3y2
x3y3
x3y3
1.二项式定理
2.二项展开式的通项
3.二项式系数:
课堂小结
1.3.1 二项式定理
创设情境
不积跬步,无以至千里;
不积小流,无以成江海。
———荀子 ·《劝学篇》
释义:做事情不一点一点积累,就永远无法达成目的。
把自己的起始优秀值看成1,假设每天的努力能让自己变得比前一天优秀1%,对优秀值进行复利计算:
第1天努力后优秀值为________________;
第2天努力后优秀值为________________;
......
第30天努力后优秀值为________________;
模型建立
1+0.01
(1+0.01)2
(1+0.01)30
估算(1+0.01)30 的近似值(精确到0.1)
探究新知
艾萨克·牛顿(1643—1727,英国)被誉为人类历史上最伟大的科学家之一,不仅是伟大的物理学家、天文学家,而且还是伟大的数学家。1664年,年仅22岁的牛顿。在数学方面就有了第一项创造性成果,就是发现了二项式定理,又称牛顿二项式定理。
探究新知
②各项中a与b次数之和呈现什么规律
①在以上各展开式中各有多少项
③各项的系数是什么
重点关注
探究新知
在初中,我们用多项式乘法法则得到了(a+b)2 的展开式,如何利用分步乘法计数原理解释上述展开过程?
?
探究
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个 (a+b) 中选a,另1个 (a+b) 中选b得到的. 由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个 (a+b) 中取1个b的组合数 ,即ab共有2个.
由2个 (a+b) 中都选b得到的. 因此,b2出现的次数相当于从2个 (a+b) 中取2个b的组合数 ,即b2只有1个.
探究新知
探究新知
同样地,如何利用分步乘法计数原理解释(a+b)3 的展开式?
?
探究
a3
a2b
a2b
a2b
b3
ab2
ab2
ab2
展开式共有:
项的形式:
探究新知
根据你发现的规律,你能写出(a+b)4 的展开式吗?
?
探究
问题:1).(a+b)4展开后各项形式分别是什么?
2).你能分析说明各项前的系数吗?
a4 a3b a2b2 ab3 b4
观察下面式子,你能猜想(a+b)n的展开式吗?
?
探究
概念形成
上述公式叫做二项式定理,右边的多项式叫做 (a+b)n 的二项展开式,其中各项的系数 叫做二项式系数.
式中 的叫做二项展开式的通项,用 表示,即通项为展开式的第 项:
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
概念形成
概念形成
1.在二项式定理中,若设a=1, b=x,则得到公式
2、把b用-b代替
求(1+0.01)30 的近似值(精确到0.1)
结论:我们每天努力1%,30天后,比现在优秀30%
解:
知识探究
例1
求 的展开式.
解:
典例分析
典例分析
例2 (1)求 (1+2x)7 的展开式的第4项;
(2)求 (1+2x)7 的展开式的第4项的系数;
(3)求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
解:
的展开式的通项为
根据题意,得
因此, x2的系数是
求 的展开式中 x2 的系数.
例3
典例分析
解:
的展开式的通项为
求 的展开式常数项的系数.
变式:
典例分析
根据题意,得
解:
求 的展开式中 x3 的系数.
例4:
典例分析
1
x2
x3
x
x3
x3
解:
求 的展开式中 x3y3 的系数.
变式:
典例分析
x
y
x2y3
x3y2
x3y3
x3y3
1.二项式定理
2.二项展开式的通项
3.二项式系数:
课堂小结
