20212022学年湖北省麻城市张家畈镇中学七年级数学第二学期期末检测模拟试题(pdf版 含解析)
文档属性
| 名称 | 20212022学年湖北省麻城市张家畈镇中学七年级数学第二学期期末检测模拟试题(pdf版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1000.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-14 13:43:14 | ||
图片预览



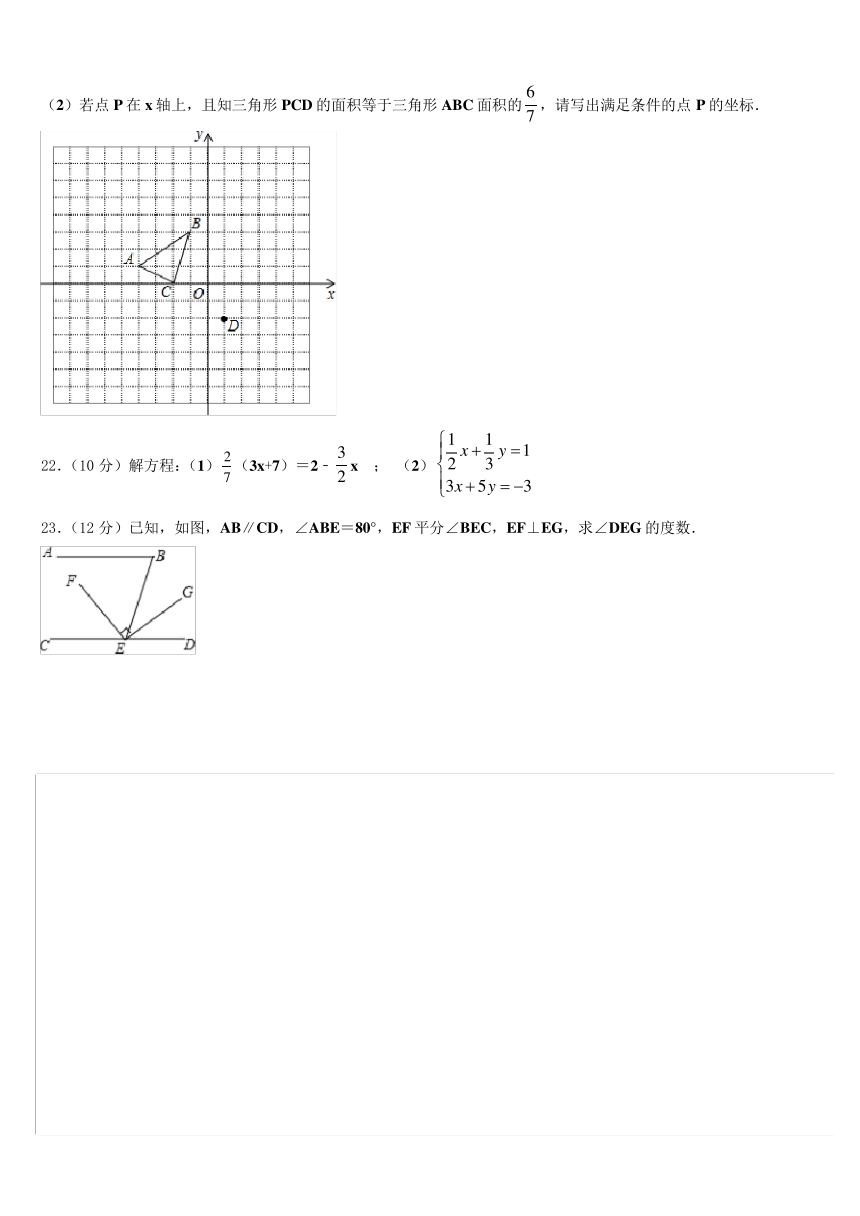

文档简介
2021-2022 学年七下数学期末模拟试卷
请考生注意:
1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答
案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共 12 个小题,每小题 3分,共 36 分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.方程 2x+1=3 的解是( )
A.x=﹣1 B.x=1 C.x=2 D.x=﹣2
2.若 a<b,则下列结论不一定成立的是( )
a b
A.a-1<b-1 B.2a<2b C. D. a2 b2
3 3
3.如图,已知△ABC 的周长是 20,OB 和 OC 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD=3,则△ABC 的面积是( )
A.20 B.25 C.30 D.35
4.在平面直角坐标系中,若点 与点 之间的距离是 5,则 的值是( )
A.2 B.-4 C.6 D.4 或-6
x y 1,
5.二元一次方程组 的解是( )
x y 3
x 2, x 1, x 3, x 1,
A. B. C. D.
y 1 y 2 y 2 y 2
6.估计 17 的值是在( )
A.3 和 4 之间 B.4 和 5 之间 C.5 和 6 之间 D.6 和 7 之间
7.每周一,同学们都要进行庄严的升旗仪式,你可以用哪幅图来近似的刻画国旗的高度与时间的关系
A. B. C.
D.
8.如图,下列条件:① ;② ;③ ;④ ;其中能判断直线 的有( )
A. 个 B. 个 C. 个 D. 个
9.如图所示,下列结论中不正确的是 ( )
A. 1和 2是同位角 B. 2和 3是同旁内角
C. 1和 4是同位角 D. 2和 4是内错角
2
10.若分式 有意义,则 x的取值范围是( )
x 5
A. x 5 B. x 5 C. x 5 D. x 5
11.下列各数中,无理数是( )
A. B. C. D.
12.若甲数为 x,乙数为 y,则“甲数的 3 倍比乙数的一半少 2”,列成方程是( )
1 1
A.3x y 2 B. y 3x 2
2 2
1 1
C.3x y 2 D. y 3x 2
2 2
二、填空题(每题 4分,满分 20 分,将答案填在答题纸上)
13.计算 x2 2xy
x的结果是__________.
14.关于 x 的不等式(a 1)x a 5 的解集与不等式 2x 4 的解集相同,则 a 的值为_____
15.已知 , ,则 的值为____.
16. 用反证法证明命题“三角形中至少有一个内角大于或等于 60°”,第一步应假设_____.
17.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正
负术和方程术.其中,方程术是《九章算术》最高的数学成就.
《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
译文:“假设有 5头牛、2只羊,值金 10 两;2头牛、5只羊,值金 8 两.问:每头牛、每只羊各值金多少两?”
设每头牛值金 x两,每只羊值金 y 两,可列方程组为_____.
三、解答题 (本大题共 7小题,共 64 分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)我市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买 A、B 两种奖品以鼓励抢答者.如
果购买 A 种 20 件,B 种 15 件,共需 380 元;如果购买 A 种 15 件,B 种 10 件,共需 280 元.
(1)A、B 两种奖品每件各多少元?
(2)现要购买 A、B 两种奖品共 100 件,总费用不超过 900 元,那么 A 种奖品最多购买多少件?
19.(5 分)如图,直线 AB∥CD ,直线 EF 分别交直线 AB 、CD 于点 E 、F ,FH 平分 EFD ,若 FEB 130 ,
求 EHF 的度数 .
20.(8 分)某中学为了丰富学生的课余生活,准备从体育用品商店一次性购买若干个排球和篮球,若购买 2 个排球和
1 个篮球共需 190 元.购买 3 个排球和 2 个篮球共需 330 元.
(1)购买一个排球、一个篮球各需多少元?
(2)根据该校的实际情况,需从体育用品商店一次性购买排球和篮球共 100 个,要求购买排球和篮球的总费用不超过
6500 元,这所中学最多可以购买多少个篮球?
21.(10 分)如图,三角形 ABC 三个顶点的坐标分别是 A(-4,1),B(-1,3),C(-2,0),将三角形 ABC 平移得
到三角形 DEF,使点 A 与点 D(1,-2)是对应点.
(1)在图中画出三角形 DEF,并写出点 B、C 的对应点 E、F 的坐标;
6
(2)若点 P 在 x 轴上,且知三角形 PCD 的面积等于三角形 ABC 面积的 ,请写出满足条件的点 P 的坐标.
7
1 1
2 3 x y 1
22.(10 分)解方程:(1) (3x+7)=2﹣ x ; (2) 2 3
7 2
3x 5y 3
23.(12 分)已知,如图,AB∥CD,∠ABE=80°,EF 平分∠BEC,EF⊥EG,求∠DEG 的度数.
参考答案
一、选择题:本大题共 12 个小题,每小题 3分,共 36 分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
【解析】
试题分析:移项,得 2x=3﹣1,合并同类项,得 2x=2,系数化为 1,得 x=1.
故选 B.
考点:一元一次方程的解.
2、D
【解析】
【分析】根据不等式的性质逐项进行判断即可得答案.
【详解】A.∵a<b,∴ a-1<b-1,正确,故 A 不符合题意;
B.∵a<b,∴ 2a<2b,正确,故 B 不符合题意;
a b
C.∵a<b,∴ ,正确,故 C 不符合题意;
3 3
D.当 a<b<0 时,a2>b2,故 D 选项错误,符合题意,
故选 D.
【点睛】本题考查了不等式的基本性质,熟练掌握不等式的性质是解题的关键.
不等式性质 1:不等式两边同时加上(或减去)同一个数,不等号方向不变;
不等式性质 2:不等式两边同时乘以(或除以)同一个正数,不等号方向不变;
不等式性质 3:不等式两边同时乘以(或除以)同一个负数,不等号方向改变.
3、C
【解析】
连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC
的距离都相等(即 OE=OD=OF),从而可得到△ABC 的面积等于周长的一半乘以 3,代入即可求解.
【详解】
如图,连接 OA,过 O 作 OE⊥AB 于 E,OF⊥AC 于 F,
∵OB、OC 分别平分∠ABC 和∠ACB,
∴OE=OF=OD=3,
∵△ABC 的周长是 20,OD⊥BC 于 D,且 OD=3,
1 1 1 1
∴S = ×AB×OE+ ×BC×OD+ ×AC×OF= ×(AB+BC+AC)×3
△ABC
2 2 2 2
1
= ×20×3=30,
2
故选 C.
【点睛】
本题考查了角平分线上的点到角的两边的距离相等的性质,判断出三角形的面积与周长的关系是解题的关键.
4、D
【解析】
若两点的纵坐标相同,则这两点间的距离即为横坐标间的距离,由此即可计算 x 的值.
【详解】
解:由题意得 即 或 ,
解得 或 .
故选:D
【点睛】
本题考查了平面直角坐标系中两点间的距离,由两点坐标的特点选择合适的距离计算方法是解题的关键.横坐标相同的
两个点 ,其距离为 ;纵坐标相同的两个点 ,其距离为 .
5、A
【解析】
根据加减消元法,可得方程组的解.
【详解】
x y 1①
,
x y 3②
①+②,得 2x=4,
解得 x=2,
把 x=2 代入①,得 2-y=1,
y=1,
x 2
所以原方程组的解为 .
y 1
故选 C.
【点睛】
本题考查了解二元一次方程组,掌握加减消元法是解题的关键.本题还可以根据二元一次方程组的解的定义,将四个
选项中每一组未知数的值代入原方程组进行检验.
6、B
【解析】
根据二次根式的概念直接解答此题.
【详解】
∵ 16< 17 < 25,∴4< 17 <5,故选:B.
【点睛】
本题考查了学生对有理数和无理数大小的比较,掌握用二次根式作为大小比较的工具是解决此题的关键.
7、B
【解析】
国旗升起的高度随时间的增大而增大,且高度在某个时间点之后应该保持不变.
【详解】
解:∵国旗升起的高度随时间的增大而增大,且高度在某个时间点之后应该保持不变,应该选 B.
故选:B.
【点睛】
本题考查函数的图象,根据题意得出国旗升起的高度与时间的函数关系是解题的关键.
8、C
【解析】
根据平行线的判定定理,对各小题进行逐一判断即可
【详解】
解:① ∠1=∠2 不能得到 ,故本条件不合题意;
② ∠4=∠5,∴ ,故本条件符合题意;
③ ∠1=∠3,∴ ,故本条件符合题意;
④ ∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴ ,故本条件符合题意.
故选:C
【点睛】
本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.
9、A
【解析】
根据同位角,内错角,同旁内角以及对顶角的定义进行解答.
【详解】
A、∠1 和∠2 是同旁内角,故本选项错误,符合题意;
B、∠2 和∠3 是同旁内角,故本选项正确,不符合题意;
C、∠1 和∠4 是同位角,故本选项正确,不符合题意;
D、∠2 和∠4 是内错角,故本选项正确,不符合题意;
故选 A.
【点睛】
考查了同位角,内错角,同旁内角以及对顶角的定义.解答此类题确定三线八角是关键,可直接从截线入手.对平面
几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它
们所包含的意义.
10、B
【解析】
根据分式有意义的条件列出关于 x 的不等式,求出 x 的取值范围即可.
【详解】
由题意得,x 5≠0,
解得 x≠5.
故选 B.
【点睛】
此题考查分式有意义的条件,解题关键在于分母不等于零.
11、C
【解析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有
限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详解】
A、 是有理数,故 A 错误;
B、 是有理数,故 B 错误;
C、 是无理数,故 C 正确;
D、 是有理数,故 D 错误;
故选:C.
【点睛】
此题考查无理数的定义,解题关键在于掌握其定义.
12、B
【解析】
1
因为“甲数的 3 倍比乙数的一半少 1”,则可列成方程 y 3x=1.
2
【详解】
1
若甲数为 x,乙数为 y,可列方程为 y 3x=1.
2
故选:B.
【点睛】
此题考查了由实际问题抽象出二元一次方程,比较容易,根据“甲数的 3 倍比乙数的一半少 1”可以直接列方程.
二、填空题(每题 4分,满分 20 分,将答案填在答题纸上)
13、 x 2y
【解析】
直接利用多项式除以单项式的法则即可求出结果,在计算的时候注意符合的问题.
【详解】
利用多项式除以单项式的法则,即
原式 x2 2xy x
= x2 x 2xy x
= x 2y
【点睛】
本题考查多项式除以单项式运算,熟练掌握运算法则是解题关键.
14、1
【解析】
由题意分别解出不等式组中的两个不等式,由题意不等式的解集为 x<2,再根据求不等式组解集的口诀:大小小大中
间找,大大小小找不到(无解)来求出 a 的范围.
【详解】
由不等式 2x<4 系数化为 1 得,
x<2,
∵不等式(a-1)x<a+5 的解集与不等式 2x<4 的解集相同,
∴a-1>0,即 a>1,
由不等式(a-1)x<a+5 知移项整理得,
a 5
x< ,与 x<2 解集相同,
a 1
a 5
∴ =2,
a 1
解得 a=1.
故答案是:1.
【点睛】
考查了一元一次不等式组解集的求法,将不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找
不到(无解)逆用,已知不等式解集反过来求 a 的值.
15、1
【解析】
将代数式变形后,再将 m+n,mn 代入即可求出答案.
【详解】
解:因为 m+n=-6,mn=4,
所以 m2-mn+n2=(m+n)2-3mn=(-6)2-3×4=36-12=1.
故答案为:1.
【点睛】
本题考查了完全平方公式.解题的关键是熟练掌握完全平方公式.
16、三角形的三个内角都小于 60°
【解析】
熟记反证法的步骤,直接填空即可.
【详解】
第一步应假设结论不成立,即三角形的三个内角都小于 60°.
故答案为三角形的三个内角都小于 60°.
【点睛】
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时,要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种
情况,则必须一一否定.
5x 2y 10
17、
2x 5y 8
【解析】
试题分析:根据“5头牛,2 只羊,值金 10两;2头牛、5 只羊,值金 8两.”列方程组即可.
考点:二元一次方程组的应用
三、解答题 (本大题共 7小题,共 64 分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)A种奖品每件 16元,B 种奖品每件 4元.(2)A 种奖品最多购买 41 件.
【解析】
【分析】(1)设 A 种奖品每件 x 元,B 种奖品每件 y 元,根据“如果购买 A 种 20 件,B 种 15 件,共需 380 元;如果购
买 A 种 15 件,B 种 10 件,共需 280 元”,即可得出关于 x、y 的二元一次方程组,解之即可得出结论;
(2)设 A 种奖品购买 a 件,则 B 种奖品购买(100﹣a)件,根据总价=单价×购买数量结合总费用不超过 900
元,即可得出关于 a 的一元一次不等式,解之取其中最大的整数即可得出结论.
【详解】(1)设 A 种奖品每件 x 元,B 种奖品每件 y 元,
20x 15y 380
根据题意得: ,
15x 10y 280
x 16
解得: ,
y 4
答:A 种奖品每件 16 元,B 种奖品每件 4 元;
(2)设 A 种奖品购买 a 件,则 B 种奖品购买(100﹣a)件,
根据题意得:16a+4(100﹣a)≤900,
125
解得:a≤ ,
3
∵a 为整数,
∴a≤41,
答:A 种奖品最多购买 41 件.
【点睛】本题考查了一元一次不等式的应用以及二元一次方程组的应用,解题的关键是:(1)找准等量关系,
正确列出二元一次方程组;(2)根据不等关系,正确列出不等式.
19、 25
【解析】
利用平行线的性质求出∠EFD,再利用角平分线的定义求出∠HFD 即可解决问题.
【详解】
解:∵ AB∥CD , FEB 130 ,
∴ EFD 50 .
∵ FH 平分 EFD ,
1 1
∴ HFD EFD 50 25 .
2 2
∵ AB∥CD ,
∴ EHF HFD 25 .
【点睛】
本题考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
20、(1)购买一个排球需 10 元、一个篮球需 90 元;(2)这所中学最多可以购买 2 个篮球.
【解析】
(1)设每个排球 x 元,每个篮球 y 元,根据“购买 2 个排球和 1 个篮球共需 190 元,购买 3 个排球和 2 个篮球共需 330
元”,即可得出关于 x,y 的二元一次方程组,解之即可得出结论;
(2)设购买篮球 a 个,则购买排球(100-a)个,根据总价=单价×数量结合购买排球和篮球的总费用不超过 6100 元,
即可得出关于 a 的一元一次不等式,解之取其中的最大值整数值即可得出结论.
【详解】
解:(1)设每个排球 x 元,每个篮球 y 元,
2x y=190
依题意,得:
3x 2y=330
x=50
解得:
y=90
答:每个排球 10 元,每个篮球 90 元.
(2)设购买篮球 a 个,则购买排球(100-a)个,
依题意,得:90a+10(100-a)≤6100,
解得:a≤2.1.
∵a 为整数,
∴a 最大取 2.
答:最多可以买 2 个篮球.
【点睛】
本题考查了二元一次方程组的应用、一元一次不等式的应用以及二元一次方程的应用,解题的关键是:(1)找准等量
关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
21、(1)作图见解析,点 E、F 的坐标分别为(4,0),(3,3);(2)P 点坐标为(1,0),(-5,0).
【解析】
(1)利用点 A 和点 D 的坐标特征确定平移的方向和距离,利用此平移规律写出 E、F 点的坐标,然后描点即可;
7 1
(2)设 P(m,0),先利用面积的和差求出 S =ABC ,则可得到 S =3,利用三角形面积公式得到PCD ×2×|m+2|=3,△ △
2 2
然后求出 m 即可得到 P 点坐标.
【详解】
解:(1)如图,△ DEF 为所作,由图可得点 E、F 的坐标分别为(4,0),(3,3);
(2)设 P(m,0),
1 1 1 7
S =3×3- ×2×1- ×3×1- ×3×2=
ABC , △
2 2 2 2
6
∵三角形 PCD 的面积等于三角形 ABC 面积的 ,
7
7 6
∴S = × =3
PCD , △
2 7
1
∴ ×2×|m+2|=3,解得 m=1 或 m=-5,
2
∴P 点坐标为(1,0),(-5,0).
【点睛】
本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,
分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
x 4
22、(1)x=0;(2) .
y 3
【解析】
(1)去分母,去括号,移项,合并同类项,系数化为 1;(2)先整理再用代入法.
【详解】
解:(1)去分母得:4(3x+7)=28﹣21x,
12x+28=28﹣21x,
12x﹣21x=28﹣28,
﹣9x=0,
x=0;
3x 2y 6(1)
(2)整理得:
3x 5y 3(2)
②﹣①得:3y=﹣9,
解得:y=﹣3,
把 y=﹣3 代入①得:3x﹣6=6,
解得:x=4,
x 4
所以原方程组的解为: .
y 3
【点睛】
考核知识点:解方程,解方程组.
23、∠DEG=40°.
【解析】
已知 AB∥CD,∠ABE=80°,根据平行线的性质求得∠BEC=100°,又因 EF 平分∠BEC,根据角平分线的定义可得
1
∠CEF= ∠BEC=50°,根据垂直的定义求得∠FEG=90°,再由平角的定义即可求得∠DEG=40°.
2
【详解】
∵AB∥CD,∠ABE=80°,
∴∠BEC=180°﹣∠ABE=100°,
∵EF 平分∠BEC,
1
∴∠CEF= ∠BEC=50°,
2
∵EF⊥EG,
∴∠FEG=90°,
∴∠DEG=180°﹣∠CEF﹣∠FEG=40°.
【点睛】
本题考查了平行线的性质、角平分线的定义、垂直的定义及平角的定义,熟练运用相关知识是解决问题的关键.
请考生注意:
1.请用 2B 铅笔将选择题答案涂填在答题纸相应位置上,请用 0.5毫米及以上黑色字迹的钢笔或签字笔将主观题的答
案写在答题纸相应的答题区内。写在试题卷、草稿纸上均无效。
2.答题前,认真阅读答题纸上的《注意事项》,按规定答题。
一、选择题:本大题共 12 个小题,每小题 3分,共 36 分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.方程 2x+1=3 的解是( )
A.x=﹣1 B.x=1 C.x=2 D.x=﹣2
2.若 a<b,则下列结论不一定成立的是( )
a b
A.a-1<b-1 B.2a<2b C. D. a2 b2
3 3
3.如图,已知△ABC 的周长是 20,OB 和 OC 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD=3,则△ABC 的面积是( )
A.20 B.25 C.30 D.35
4.在平面直角坐标系中,若点 与点 之间的距离是 5,则 的值是( )
A.2 B.-4 C.6 D.4 或-6
x y 1,
5.二元一次方程组 的解是( )
x y 3
x 2, x 1, x 3, x 1,
A. B. C. D.
y 1 y 2 y 2 y 2
6.估计 17 的值是在( )
A.3 和 4 之间 B.4 和 5 之间 C.5 和 6 之间 D.6 和 7 之间
7.每周一,同学们都要进行庄严的升旗仪式,你可以用哪幅图来近似的刻画国旗的高度与时间的关系
A. B. C.
D.
8.如图,下列条件:① ;② ;③ ;④ ;其中能判断直线 的有( )
A. 个 B. 个 C. 个 D. 个
9.如图所示,下列结论中不正确的是 ( )
A. 1和 2是同位角 B. 2和 3是同旁内角
C. 1和 4是同位角 D. 2和 4是内错角
2
10.若分式 有意义,则 x的取值范围是( )
x 5
A. x 5 B. x 5 C. x 5 D. x 5
11.下列各数中,无理数是( )
A. B. C. D.
12.若甲数为 x,乙数为 y,则“甲数的 3 倍比乙数的一半少 2”,列成方程是( )
1 1
A.3x y 2 B. y 3x 2
2 2
1 1
C.3x y 2 D. y 3x 2
2 2
二、填空题(每题 4分,满分 20 分,将答案填在答题纸上)
13.计算 x2 2xy
x的结果是__________.
14.关于 x 的不等式(a 1)x a 5 的解集与不等式 2x 4 的解集相同,则 a 的值为_____
15.已知 , ,则 的值为____.
16. 用反证法证明命题“三角形中至少有一个内角大于或等于 60°”,第一步应假设_____.
17.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正
负术和方程术.其中,方程术是《九章算术》最高的数学成就.
《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”
译文:“假设有 5头牛、2只羊,值金 10 两;2头牛、5只羊,值金 8 两.问:每头牛、每只羊各值金多少两?”
设每头牛值金 x两,每只羊值金 y 两,可列方程组为_____.
三、解答题 (本大题共 7小题,共 64 分.解答应写出文字说明、证明过程或演算步骤.)
18.(5分)我市正在创建“全国文明城市”,某校拟举办“创文知识”抢答赛,欲购买 A、B 两种奖品以鼓励抢答者.如
果购买 A 种 20 件,B 种 15 件,共需 380 元;如果购买 A 种 15 件,B 种 10 件,共需 280 元.
(1)A、B 两种奖品每件各多少元?
(2)现要购买 A、B 两种奖品共 100 件,总费用不超过 900 元,那么 A 种奖品最多购买多少件?
19.(5 分)如图,直线 AB∥CD ,直线 EF 分别交直线 AB 、CD 于点 E 、F ,FH 平分 EFD ,若 FEB 130 ,
求 EHF 的度数 .
20.(8 分)某中学为了丰富学生的课余生活,准备从体育用品商店一次性购买若干个排球和篮球,若购买 2 个排球和
1 个篮球共需 190 元.购买 3 个排球和 2 个篮球共需 330 元.
(1)购买一个排球、一个篮球各需多少元?
(2)根据该校的实际情况,需从体育用品商店一次性购买排球和篮球共 100 个,要求购买排球和篮球的总费用不超过
6500 元,这所中学最多可以购买多少个篮球?
21.(10 分)如图,三角形 ABC 三个顶点的坐标分别是 A(-4,1),B(-1,3),C(-2,0),将三角形 ABC 平移得
到三角形 DEF,使点 A 与点 D(1,-2)是对应点.
(1)在图中画出三角形 DEF,并写出点 B、C 的对应点 E、F 的坐标;
6
(2)若点 P 在 x 轴上,且知三角形 PCD 的面积等于三角形 ABC 面积的 ,请写出满足条件的点 P 的坐标.
7
1 1
2 3 x y 1
22.(10 分)解方程:(1) (3x+7)=2﹣ x ; (2) 2 3
7 2
3x 5y 3
23.(12 分)已知,如图,AB∥CD,∠ABE=80°,EF 平分∠BEC,EF⊥EG,求∠DEG 的度数.
参考答案
一、选择题:本大题共 12 个小题,每小题 3分,共 36 分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、B
【解析】
试题分析:移项,得 2x=3﹣1,合并同类项,得 2x=2,系数化为 1,得 x=1.
故选 B.
考点:一元一次方程的解.
2、D
【解析】
【分析】根据不等式的性质逐项进行判断即可得答案.
【详解】A.∵a<b,∴ a-1<b-1,正确,故 A 不符合题意;
B.∵a<b,∴ 2a<2b,正确,故 B 不符合题意;
a b
C.∵a<b,∴ ,正确,故 C 不符合题意;
3 3
D.当 a<b<0 时,a2>b2,故 D 选项错误,符合题意,
故选 D.
【点睛】本题考查了不等式的基本性质,熟练掌握不等式的性质是解题的关键.
不等式性质 1:不等式两边同时加上(或减去)同一个数,不等号方向不变;
不等式性质 2:不等式两边同时乘以(或除以)同一个正数,不等号方向不变;
不等式性质 3:不等式两边同时乘以(或除以)同一个负数,不等号方向改变.
3、C
【解析】
连接OA,过O作OE⊥AB于E,OF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC
的距离都相等(即 OE=OD=OF),从而可得到△ABC 的面积等于周长的一半乘以 3,代入即可求解.
【详解】
如图,连接 OA,过 O 作 OE⊥AB 于 E,OF⊥AC 于 F,
∵OB、OC 分别平分∠ABC 和∠ACB,
∴OE=OF=OD=3,
∵△ABC 的周长是 20,OD⊥BC 于 D,且 OD=3,
1 1 1 1
∴S = ×AB×OE+ ×BC×OD+ ×AC×OF= ×(AB+BC+AC)×3
△ABC
2 2 2 2
1
= ×20×3=30,
2
故选 C.
【点睛】
本题考查了角平分线上的点到角的两边的距离相等的性质,判断出三角形的面积与周长的关系是解题的关键.
4、D
【解析】
若两点的纵坐标相同,则这两点间的距离即为横坐标间的距离,由此即可计算 x 的值.
【详解】
解:由题意得 即 或 ,
解得 或 .
故选:D
【点睛】
本题考查了平面直角坐标系中两点间的距离,由两点坐标的特点选择合适的距离计算方法是解题的关键.横坐标相同的
两个点 ,其距离为 ;纵坐标相同的两个点 ,其距离为 .
5、A
【解析】
根据加减消元法,可得方程组的解.
【详解】
x y 1①
,
x y 3②
①+②,得 2x=4,
解得 x=2,
把 x=2 代入①,得 2-y=1,
y=1,
x 2
所以原方程组的解为 .
y 1
故选 C.
【点睛】
本题考查了解二元一次方程组,掌握加减消元法是解题的关键.本题还可以根据二元一次方程组的解的定义,将四个
选项中每一组未知数的值代入原方程组进行检验.
6、B
【解析】
根据二次根式的概念直接解答此题.
【详解】
∵ 16< 17 < 25,∴4< 17 <5,故选:B.
【点睛】
本题考查了学生对有理数和无理数大小的比较,掌握用二次根式作为大小比较的工具是解决此题的关键.
7、B
【解析】
国旗升起的高度随时间的增大而增大,且高度在某个时间点之后应该保持不变.
【详解】
解:∵国旗升起的高度随时间的增大而增大,且高度在某个时间点之后应该保持不变,应该选 B.
故选:B.
【点睛】
本题考查函数的图象,根据题意得出国旗升起的高度与时间的函数关系是解题的关键.
8、C
【解析】
根据平行线的判定定理,对各小题进行逐一判断即可
【详解】
解:① ∠1=∠2 不能得到 ,故本条件不合题意;
② ∠4=∠5,∴ ,故本条件符合题意;
③ ∠1=∠3,∴ ,故本条件符合题意;
④ ∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴ ,故本条件符合题意.
故选:C
【点睛】
本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.
9、A
【解析】
根据同位角,内错角,同旁内角以及对顶角的定义进行解答.
【详解】
A、∠1 和∠2 是同旁内角,故本选项错误,符合题意;
B、∠2 和∠3 是同旁内角,故本选项正确,不符合题意;
C、∠1 和∠4 是同位角,故本选项正确,不符合题意;
D、∠2 和∠4 是内错角,故本选项正确,不符合题意;
故选 A.
【点睛】
考查了同位角,内错角,同旁内角以及对顶角的定义.解答此类题确定三线八角是关键,可直接从截线入手.对平面
几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它
们所包含的意义.
10、B
【解析】
根据分式有意义的条件列出关于 x 的不等式,求出 x 的取值范围即可.
【详解】
由题意得,x 5≠0,
解得 x≠5.
故选 B.
【点睛】
此题考查分式有意义的条件,解题关键在于分母不等于零.
11、C
【解析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有
限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【详解】
A、 是有理数,故 A 错误;
B、 是有理数,故 B 错误;
C、 是无理数,故 C 正确;
D、 是有理数,故 D 错误;
故选:C.
【点睛】
此题考查无理数的定义,解题关键在于掌握其定义.
12、B
【解析】
1
因为“甲数的 3 倍比乙数的一半少 1”,则可列成方程 y 3x=1.
2
【详解】
1
若甲数为 x,乙数为 y,可列方程为 y 3x=1.
2
故选:B.
【点睛】
此题考查了由实际问题抽象出二元一次方程,比较容易,根据“甲数的 3 倍比乙数的一半少 1”可以直接列方程.
二、填空题(每题 4分,满分 20 分,将答案填在答题纸上)
13、 x 2y
【解析】
直接利用多项式除以单项式的法则即可求出结果,在计算的时候注意符合的问题.
【详解】
利用多项式除以单项式的法则,即
原式 x2 2xy x
= x2 x 2xy x
= x 2y
【点睛】
本题考查多项式除以单项式运算,熟练掌握运算法则是解题关键.
14、1
【解析】
由题意分别解出不等式组中的两个不等式,由题意不等式的解集为 x<2,再根据求不等式组解集的口诀:大小小大中
间找,大大小小找不到(无解)来求出 a 的范围.
【详解】
由不等式 2x<4 系数化为 1 得,
x<2,
∵不等式(a-1)x<a+5 的解集与不等式 2x<4 的解集相同,
∴a-1>0,即 a>1,
由不等式(a-1)x<a+5 知移项整理得,
a 5
x< ,与 x<2 解集相同,
a 1
a 5
∴ =2,
a 1
解得 a=1.
故答案是:1.
【点睛】
考查了一元一次不等式组解集的求法,将不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找
不到(无解)逆用,已知不等式解集反过来求 a 的值.
15、1
【解析】
将代数式变形后,再将 m+n,mn 代入即可求出答案.
【详解】
解:因为 m+n=-6,mn=4,
所以 m2-mn+n2=(m+n)2-3mn=(-6)2-3×4=36-12=1.
故答案为:1.
【点睛】
本题考查了完全平方公式.解题的关键是熟练掌握完全平方公式.
16、三角形的三个内角都小于 60°
【解析】
熟记反证法的步骤,直接填空即可.
【详解】
第一步应假设结论不成立,即三角形的三个内角都小于 60°.
故答案为三角形的三个内角都小于 60°.
【点睛】
反证法的步骤是:
(1)假设结论不成立;
(2)从假设出发推出矛盾;
(3)假设不成立,则结论成立.
在假设结论不成立时,要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种
情况,则必须一一否定.
5x 2y 10
17、
2x 5y 8
【解析】
试题分析:根据“5头牛,2 只羊,值金 10两;2头牛、5 只羊,值金 8两.”列方程组即可.
考点:二元一次方程组的应用
三、解答题 (本大题共 7小题,共 64 分.解答应写出文字说明、证明过程或演算步骤.)
18、(1)A种奖品每件 16元,B 种奖品每件 4元.(2)A 种奖品最多购买 41 件.
【解析】
【分析】(1)设 A 种奖品每件 x 元,B 种奖品每件 y 元,根据“如果购买 A 种 20 件,B 种 15 件,共需 380 元;如果购
买 A 种 15 件,B 种 10 件,共需 280 元”,即可得出关于 x、y 的二元一次方程组,解之即可得出结论;
(2)设 A 种奖品购买 a 件,则 B 种奖品购买(100﹣a)件,根据总价=单价×购买数量结合总费用不超过 900
元,即可得出关于 a 的一元一次不等式,解之取其中最大的整数即可得出结论.
【详解】(1)设 A 种奖品每件 x 元,B 种奖品每件 y 元,
20x 15y 380
根据题意得: ,
15x 10y 280
x 16
解得: ,
y 4
答:A 种奖品每件 16 元,B 种奖品每件 4 元;
(2)设 A 种奖品购买 a 件,则 B 种奖品购买(100﹣a)件,
根据题意得:16a+4(100﹣a)≤900,
125
解得:a≤ ,
3
∵a 为整数,
∴a≤41,
答:A 种奖品最多购买 41 件.
【点睛】本题考查了一元一次不等式的应用以及二元一次方程组的应用,解题的关键是:(1)找准等量关系,
正确列出二元一次方程组;(2)根据不等关系,正确列出不等式.
19、 25
【解析】
利用平行线的性质求出∠EFD,再利用角平分线的定义求出∠HFD 即可解决问题.
【详解】
解:∵ AB∥CD , FEB 130 ,
∴ EFD 50 .
∵ FH 平分 EFD ,
1 1
∴ HFD EFD 50 25 .
2 2
∵ AB∥CD ,
∴ EHF HFD 25 .
【点睛】
本题考查平行线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.
20、(1)购买一个排球需 10 元、一个篮球需 90 元;(2)这所中学最多可以购买 2 个篮球.
【解析】
(1)设每个排球 x 元,每个篮球 y 元,根据“购买 2 个排球和 1 个篮球共需 190 元,购买 3 个排球和 2 个篮球共需 330
元”,即可得出关于 x,y 的二元一次方程组,解之即可得出结论;
(2)设购买篮球 a 个,则购买排球(100-a)个,根据总价=单价×数量结合购买排球和篮球的总费用不超过 6100 元,
即可得出关于 a 的一元一次不等式,解之取其中的最大值整数值即可得出结论.
【详解】
解:(1)设每个排球 x 元,每个篮球 y 元,
2x y=190
依题意,得:
3x 2y=330
x=50
解得:
y=90
答:每个排球 10 元,每个篮球 90 元.
(2)设购买篮球 a 个,则购买排球(100-a)个,
依题意,得:90a+10(100-a)≤6100,
解得:a≤2.1.
∵a 为整数,
∴a 最大取 2.
答:最多可以买 2 个篮球.
【点睛】
本题考查了二元一次方程组的应用、一元一次不等式的应用以及二元一次方程的应用,解题的关键是:(1)找准等量
关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.
21、(1)作图见解析,点 E、F 的坐标分别为(4,0),(3,3);(2)P 点坐标为(1,0),(-5,0).
【解析】
(1)利用点 A 和点 D 的坐标特征确定平移的方向和距离,利用此平移规律写出 E、F 点的坐标,然后描点即可;
7 1
(2)设 P(m,0),先利用面积的和差求出 S =ABC ,则可得到 S =3,利用三角形面积公式得到PCD ×2×|m+2|=3,△ △
2 2
然后求出 m 即可得到 P 点坐标.
【详解】
解:(1)如图,△ DEF 为所作,由图可得点 E、F 的坐标分别为(4,0),(3,3);
(2)设 P(m,0),
1 1 1 7
S =3×3- ×2×1- ×3×1- ×3×2=
ABC , △
2 2 2 2
6
∵三角形 PCD 的面积等于三角形 ABC 面积的 ,
7
7 6
∴S = × =3
PCD , △
2 7
1
∴ ×2×|m+2|=3,解得 m=1 或 m=-5,
2
∴P 点坐标为(1,0),(-5,0).
【点睛】
本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,
分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
x 4
22、(1)x=0;(2) .
y 3
【解析】
(1)去分母,去括号,移项,合并同类项,系数化为 1;(2)先整理再用代入法.
【详解】
解:(1)去分母得:4(3x+7)=28﹣21x,
12x+28=28﹣21x,
12x﹣21x=28﹣28,
﹣9x=0,
x=0;
3x 2y 6(1)
(2)整理得:
3x 5y 3(2)
②﹣①得:3y=﹣9,
解得:y=﹣3,
把 y=﹣3 代入①得:3x﹣6=6,
解得:x=4,
x 4
所以原方程组的解为: .
y 3
【点睛】
考核知识点:解方程,解方程组.
23、∠DEG=40°.
【解析】
已知 AB∥CD,∠ABE=80°,根据平行线的性质求得∠BEC=100°,又因 EF 平分∠BEC,根据角平分线的定义可得
1
∠CEF= ∠BEC=50°,根据垂直的定义求得∠FEG=90°,再由平角的定义即可求得∠DEG=40°.
2
【详解】
∵AB∥CD,∠ABE=80°,
∴∠BEC=180°﹣∠ABE=100°,
∵EF 平分∠BEC,
1
∴∠CEF= ∠BEC=50°,
2
∵EF⊥EG,
∴∠FEG=90°,
∴∠DEG=180°﹣∠CEF﹣∠FEG=40°.
【点睛】
本题考查了平行线的性质、角平分线的定义、垂直的定义及平角的定义,熟练运用相关知识是解决问题的关键.
同课章节目录
