回归分析[下学期]
图片预览




文档简介
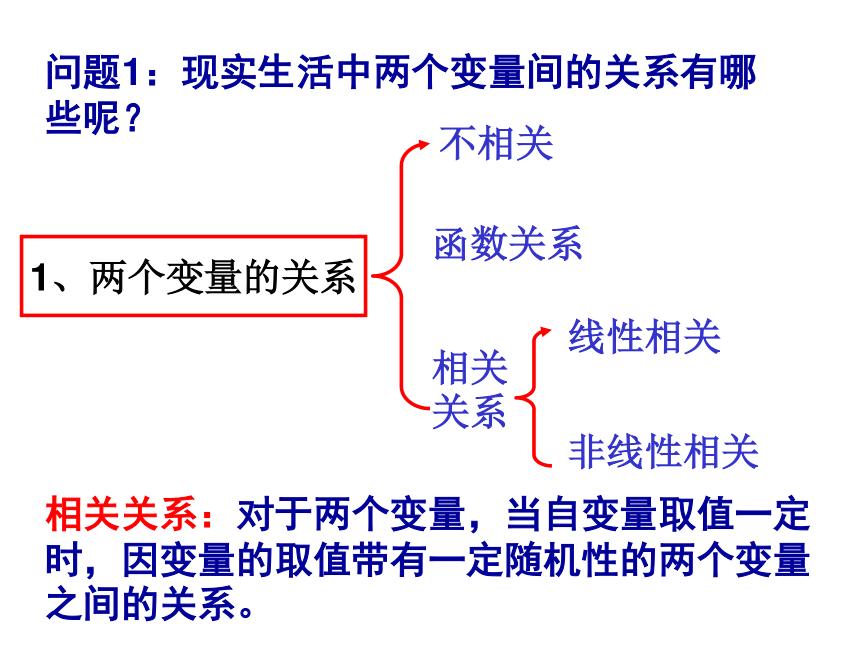
课件14张PPT。回归分析1、两个变量的关系不相关相关关系函数关系线性相关非线性相关问题1:现实生活中两个变量间的关系有哪些呢?相关关系:对于两个变量,当自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系。思考:相关关系与函数关系有怎样的不同?函数关系中的两个变量间是一种确定性关系
相关关系是一种非确定性关系 函数关系是一种理想的关系模型
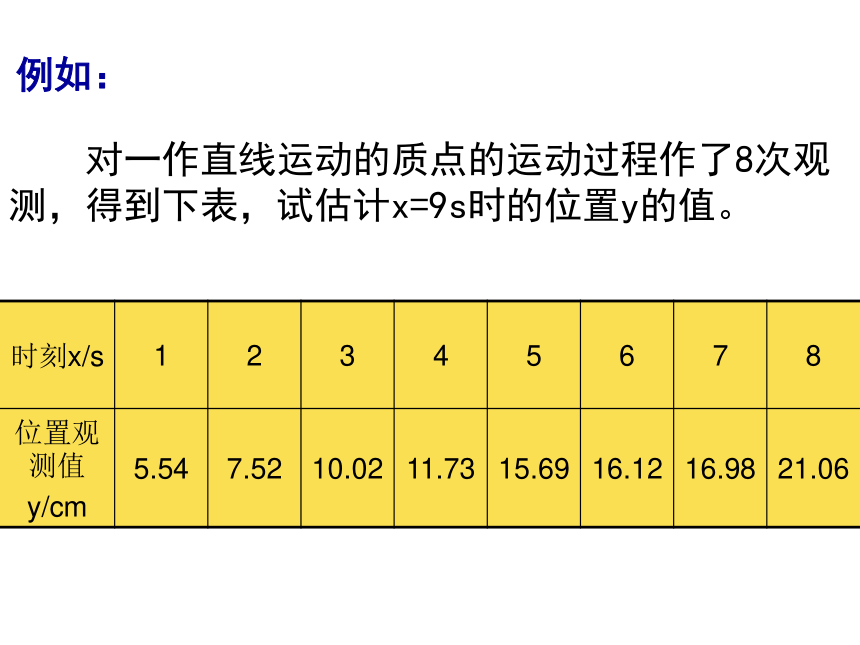
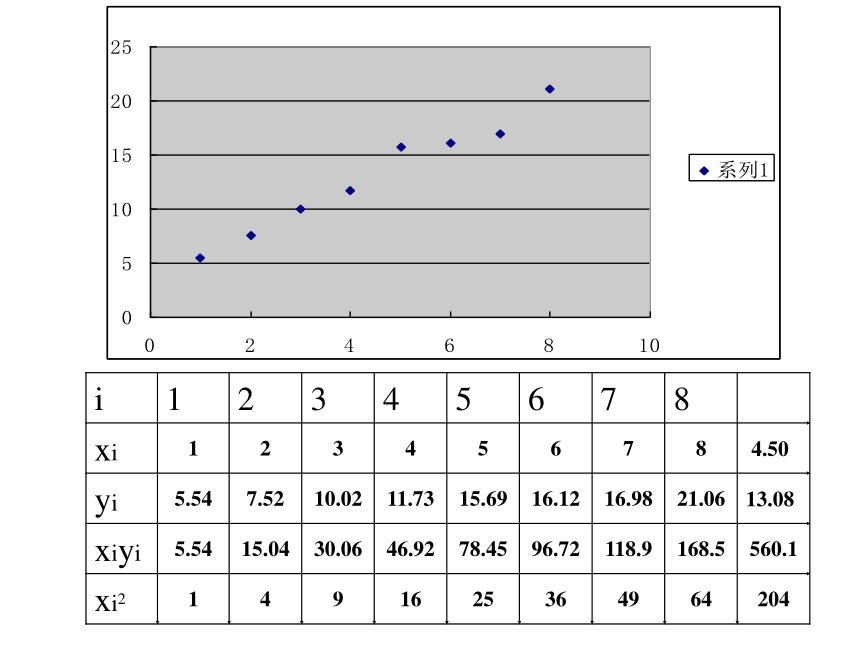
相关关系在现实生活中大量存在,是更一般的情况问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?2、最小二乘估计最小二乘估计下的线性回归方程: 对一作直线运动的质点的运动过程作了8次观测,得到下表,试估计x=9s时的位置y的值。例如:根据线性回归的系数公式,可以得到a=3.5361,b=2.1214得到线性回归方程 =3.5361+2.1214 x当x=9时,可以估计其位置值为22.6287.3、回归分析的基本步骤:画散点图求回归方程预报、决策数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
用回归直线方程解决应用问题4、线性回归模型其中a+bx是确定性函数, ? 是随机误差注:? 产生的主要原因:
(1)所用确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)观测误差。思考:在时刻x=9s时,质点运动位置一定是22.6287cm吗?例题1.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得数据如下:(1)y与x是否具有线性相关?
(2)若y与x具有线性相关关系,求回归直线方程
(3)预测加工200个零件需花费多少时间?分析:这是一个回归分析问题,应先进行线性相关检验或作散点图来判断x与y是否具有线性相关才可以求解后面的问题。作散点图如下:不难看出x,y成线性相关。解(1)列出下表:问题:有时散点图的各点并不集中在一条直线的附近,仍然可以按照求回归直线方程的步骤求回归直线,显然这样的回归直线没有实际意义。在怎样的情况下求得的回归直线方程才有实际意义?即建立的线性回归模型是否合理?如何对一组数据之间的线性相关程度作出定量分析?
相关关系是一种非确定性关系 函数关系是一种理想的关系模型
相关关系在现实生活中大量存在,是更一般的情况问题2:对于线性相关的两个变量用什么方法来刻划之间的关系呢?2、最小二乘估计最小二乘估计下的线性回归方程: 对一作直线运动的质点的运动过程作了8次观测,得到下表,试估计x=9s时的位置y的值。例如:根据线性回归的系数公式,可以得到a=3.5361,b=2.1214得到线性回归方程 =3.5361+2.1214 x当x=9时,可以估计其位置值为22.6287.3、回归分析的基本步骤:画散点图求回归方程预报、决策数学3——统计
画散点图
了解最小二乘法的思想
求回归直线方程
用回归直线方程解决应用问题4、线性回归模型其中a+bx是确定性函数, ? 是随机误差注:? 产生的主要原因:
(1)所用确定性函数不恰当;
(2)忽略了某些因素的影响;
(3)观测误差。思考:在时刻x=9s时,质点运动位置一定是22.6287cm吗?例题1.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,测得数据如下:(1)y与x是否具有线性相关?
(2)若y与x具有线性相关关系,求回归直线方程
(3)预测加工200个零件需花费多少时间?分析:这是一个回归分析问题,应先进行线性相关检验或作散点图来判断x与y是否具有线性相关才可以求解后面的问题。作散点图如下:不难看出x,y成线性相关。解(1)列出下表:问题:有时散点图的各点并不集中在一条直线的附近,仍然可以按照求回归直线方程的步骤求回归直线,显然这样的回归直线没有实际意义。在怎样的情况下求得的回归直线方程才有实际意义?即建立的线性回归模型是否合理?如何对一组数据之间的线性相关程度作出定量分析?
