合情推理-类比推理[下学期]
图片预览




文档简介
课件10张PPT。§2.1.1 合情推理1.推理是人们思维活动的过程,是根
据一个或多个已知的判断来确定一个
新的思维过程。一、知识回顾4.归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理称为归纳推理。二、类比推理1.请同学们阅读课本P30-322.类比推理:由两种对象具有某些类
似特征,推出另一类对象也有这些
特征的推理称为类比推理(类比)。三、应用举例球的表面积球的体积球心与小圆圆心的连线垂
直于球的小圆与球心距离相等的两圆相
等,与球心距离不等的两
圆不等,距球心较近的小
圆较大。以点(x0,y0)为球心,r为
半径的球的方程为(x-x0)2
+(y-y0)2+(z-z0)2=r2。例2.类比实数的加法和乘法,列出它
们相似的运算性质。解:⑴两个实数的两种运算结果仍然
是一个实数。⑵两种运算都满足交换律、结合律,即:a+b=b+aa×b=b×a(a+b)+c=a+(b+c)(a×b)×c=a×(b×c)⑶两种运算都有逆运算:x=-ax=1/a(a≠0)⑷两种运算都有运算的恒等性(不变
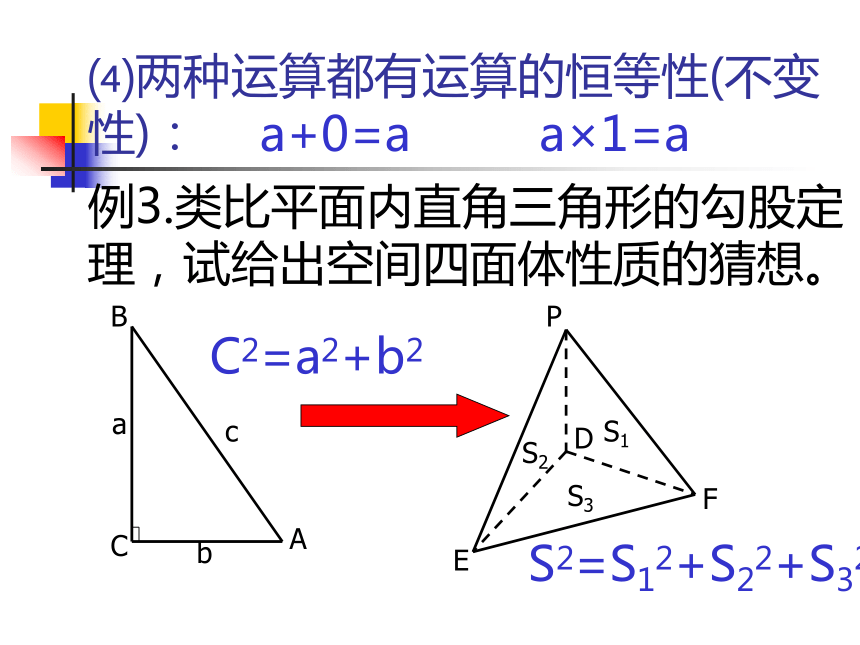
性):a+0=aa×1=a例3.类比平面内直角三角形的勾股定
理,试给出空间四面体性质的猜想。C2=a2+b2S2=S12+S22+S32四、课堂小结从具体问题出发推理过程为:观察、分析、
比较、联想归纳、类比提出猜想归纳推理和类比推
理统称合情推理。
即:“合乎情理”的
推理。五、课堂练习课本P38 练习:3。四面体任意三个面之和大于
第四个面四面体的中位面的面积等于第四
面面积的1/4,且平行于第四面四面体的六个二面角的平分面
交于一点,且这个点是四面体
内且球的球心四面体的体积为
V=1/3(S1+S2+S3+S4)r
(S1,S2,S3,S4为四个面的面积,
r为内切球的半径)六、课外作业课本P44 习题2.1 A组:5、6。
B组:1。1,一个多面体有10个顶点,7个面,那么它的棱
数为( )-sin(x)3,三角形的面积为s=1/2(a+b+c)r(r为三角形内
切圆的半径,a,b,c为三边长)利用类比推理可
以得出四面体的体积为( )4,10条直线最多可以有( )个交点45
据一个或多个已知的判断来确定一个
新的思维过程。一、知识回顾4.归纳推理:由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理称为归纳推理。二、类比推理1.请同学们阅读课本P30-322.类比推理:由两种对象具有某些类
似特征,推出另一类对象也有这些
特征的推理称为类比推理(类比)。三、应用举例球的表面积球的体积球心与小圆圆心的连线垂
直于球的小圆与球心距离相等的两圆相
等,与球心距离不等的两
圆不等,距球心较近的小
圆较大。以点(x0,y0)为球心,r为
半径的球的方程为(x-x0)2
+(y-y0)2+(z-z0)2=r2。例2.类比实数的加法和乘法,列出它
们相似的运算性质。解:⑴两个实数的两种运算结果仍然
是一个实数。⑵两种运算都满足交换律、结合律,即:a+b=b+aa×b=b×a(a+b)+c=a+(b+c)(a×b)×c=a×(b×c)⑶两种运算都有逆运算:x=-ax=1/a(a≠0)⑷两种运算都有运算的恒等性(不变
性):a+0=aa×1=a例3.类比平面内直角三角形的勾股定
理,试给出空间四面体性质的猜想。C2=a2+b2S2=S12+S22+S32四、课堂小结从具体问题出发推理过程为:观察、分析、
比较、联想归纳、类比提出猜想归纳推理和类比推
理统称合情推理。
即:“合乎情理”的
推理。五、课堂练习课本P38 练习:3。四面体任意三个面之和大于
第四个面四面体的中位面的面积等于第四
面面积的1/4,且平行于第四面四面体的六个二面角的平分面
交于一点,且这个点是四面体
内且球的球心四面体的体积为
V=1/3(S1+S2+S3+S4)r
(S1,S2,S3,S4为四个面的面积,
r为内切球的半径)六、课外作业课本P44 习题2.1 A组:5、6。
B组:1。1,一个多面体有10个顶点,7个面,那么它的棱
数为( )-sin(x)3,三角形的面积为s=1/2(a+b+c)r(r为三角形内
切圆的半径,a,b,c为三边长)利用类比推理可
以得出四面体的体积为( )4,10条直线最多可以有( )个交点45
