2.1.1合情推理-类比推理[下学期]
文档属性
| 名称 | 2.1.1合情推理-类比推理[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 277.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-04-24 13:20:00 | ||
图片预览










文档简介
课件32张PPT。2.1.2 类比推理1.合情推理的主要形式有 和 .2.归纳推理是从 事实中概括出 结论的一种推理模式.归纳推理的思维过程大致是:归纳类比个别一般类比推理“快回火星吧,
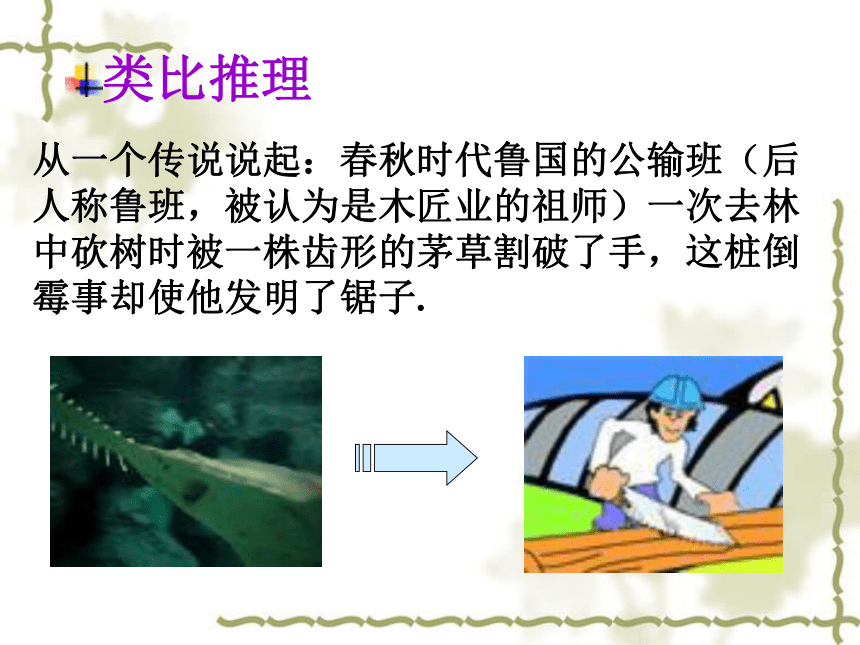
地球是很危险滴” 类比推理的定义可能存在生命类比推理从一个传说说起:春秋时代鲁国的公输班(后人称鲁班,被认为是木匠业的祖师)一次去林中砍树时被一株齿形的茅草割破了手,这桩倒霉事却使他发明了锯子.类比推理茅草是齿形的;茅草能割破手.我需要一种能割断木头的工具;它也可以是齿形的.鲁班的思路是这样的:这个推理过程是归纳推理吗?问题:试根据等式的性质猜想不等式的性质。等式的性质:
(1) a=b?a+c=b+c;
(2) a=b? ac=bc;
(3) a=b?a2=b2;等等。猜想不等式的性质:(1) a>b?a+c>b+c;(2) a>b? ac>bc;(3) a>b?a2>b2;等等。问:这样猜想出的结论是否一定正确?类比推理
这种由两个(两类)对象之间在某些方面的相似或相同,推演出他们在其他方面也相似或相同;或其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比).
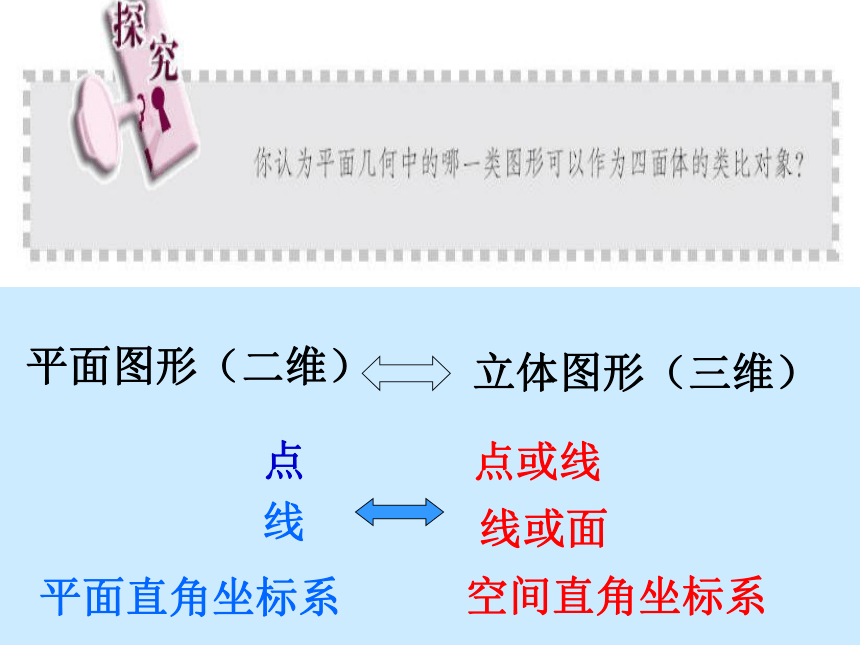
简言之,类比推理是由特殊到特殊的推理.类比推理的定义:1.工匠鲁班类比带齿的草叶和蝗虫的牙齿,发明了锯2.仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.3.科学家对火星进行研究,发现火星与地球有许多类似的特征; 1)火星也绕太阳运行、饶轴自转的行星; 2)有大气层,在一年中也有季节变更; 3)火星上大部分时间的温度适合地球上某些已知生物的生存,等等. 科学家猜想;火星上也可能有生命存在.类比推理 类比推理举例构成几何体的元素数目:四面体 三角形 平面图形(二维)立体图形(三维)点点或线线线或面平面直角坐标系空间直角坐标系 类比推理举例构成几何体的元素数目:四面体 三角形 类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S优化设计P61~~~~5
P62~~~~6
P62~~~~下7
P65~~~~3,4
P65~~~~右3
P66~~~~4,8几何中常见的类比对象三角形四面体(各面均为三角形)四边形六面体(各面均为四边形)圆球代数中常见的类比对象复数向量方程函数不等式交集,并集,补集或,且,非运算例1.(2003年新课程)在平面几何里,有勾股定理:
“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则 .利用平面向量的性质类比得空间向量的性质利用等差数列性质类比等比数列性质类比推理 “类比是一个伟大的引路人,求解立体几何往往有赖于平面几何的类比问题.”
————数学家波利亚 例4.在平面上,设ha,hb,hc是三角形ABC三条边上的高.P为三角形内任一点,P到相应三边的距离分别为pa,pb,pc,我们可以得到结论:
试通过类比,写出在空间中的类似结论.ABCPpapbpcABCDP例1、试将平面上的圆与空间的球进行类比.圆的定义:平面内到一个定点的距离等于定长的点的集合.球的定义:到一个定点的距离等于定长的点的集合.圆
弦
直径周长
面积球
截面圆大圆表面积体积圆的概念和性质球的概念和性质与圆心距离相等的两弦相等与圆心距离不相等的两弦不相等,距圆心较近的弦较长以点(x0,y0)为圆心, r为半径的圆的方程为(x-x0)2+(y-y0)2 = r2圆心与弦(非直径)中点的连线垂直于弦球心与不过球心的截面(圆面)的圆点的连线垂直于截面与球心距离相等的两截面面积相等与球心距离不相等的两截面面积不相等,距球心较近的面积较大以点(x0,y0,z0)为球心, r为半径的球的方程为(x-x0)2+(y-y0)2+(z-z0)2 = r2利用圆的性质类比得出求的性质例题讲解c2 = a2+b2例3.有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
1.每次只能移动一个金属片;
2.较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?n=1时,n=2时,n=1时,n=3时,n=2时,n=1时,n=2时,n=1时,n=3时,n=4时,n=3时,n=2时,n=1时,古印度有一個傳說,婆羅賀摩(Brahma,眾生之父)在Berares地方的廟宇安置了一個含有64個金盤的婆羅賀摩塔,婆羅門教的憎侶們,奉命依遊戲規則要不停移動這些金盤,傳說中還說,當重排完成時,就是世界末日的到來,而經過計算,這64個金盤的遊戲至少要經過 264-1次才會完成,如果移動一次以1秒鐘計算,還要經過184467440737095551615天才能完成,照這樣看來,這世界還算蠻安全的。球心与截面圆(不是大圆)的圆点的连线垂直于截面圆与球心距离相等的两截面圆相等;与球心距离不等的两截面圆不等,距球心较近的截面圆较大球的切面垂直于过切点的半径;经过球心且垂直于切面的直线必经过切点经过切点且垂直于切面的直线必经过球心
地球是很危险滴” 类比推理的定义可能存在生命类比推理从一个传说说起:春秋时代鲁国的公输班(后人称鲁班,被认为是木匠业的祖师)一次去林中砍树时被一株齿形的茅草割破了手,这桩倒霉事却使他发明了锯子.类比推理茅草是齿形的;茅草能割破手.我需要一种能割断木头的工具;它也可以是齿形的.鲁班的思路是这样的:这个推理过程是归纳推理吗?问题:试根据等式的性质猜想不等式的性质。等式的性质:
(1) a=b?a+c=b+c;
(2) a=b? ac=bc;
(3) a=b?a2=b2;等等。猜想不等式的性质:(1) a>b?a+c>b+c;(2) a>b? ac>bc;(3) a>b?a2>b2;等等。问:这样猜想出的结论是否一定正确?类比推理
这种由两个(两类)对象之间在某些方面的相似或相同,推演出他们在其他方面也相似或相同;或其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比).
简言之,类比推理是由特殊到特殊的推理.类比推理的定义:1.工匠鲁班类比带齿的草叶和蝗虫的牙齿,发明了锯2.仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.3.科学家对火星进行研究,发现火星与地球有许多类似的特征; 1)火星也绕太阳运行、饶轴自转的行星; 2)有大气层,在一年中也有季节变更; 3)火星上大部分时间的温度适合地球上某些已知生物的生存,等等. 科学家猜想;火星上也可能有生命存在.类比推理 类比推理举例构成几何体的元素数目:四面体 三角形 平面图形(二维)立体图形(三维)点点或线线线或面平面直角坐标系空间直角坐标系 类比推理举例构成几何体的元素数目:四面体 三角形 类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S优化设计P61~~~~5
P62~~~~6
P62~~~~下7
P65~~~~3,4
P65~~~~右3
P66~~~~4,8几何中常见的类比对象三角形四面体(各面均为三角形)四边形六面体(各面均为四边形)圆球代数中常见的类比对象复数向量方程函数不等式交集,并集,补集或,且,非运算例1.(2003年新课程)在平面几何里,有勾股定理:
“设△ABC的两边AB、AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的侧面面积与底面面积的关系,可以得出的正确结论是“设三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则 .利用平面向量的性质类比得空间向量的性质利用等差数列性质类比等比数列性质类比推理 “类比是一个伟大的引路人,求解立体几何往往有赖于平面几何的类比问题.”
————数学家波利亚 例4.在平面上,设ha,hb,hc是三角形ABC三条边上的高.P为三角形内任一点,P到相应三边的距离分别为pa,pb,pc,我们可以得到结论:
试通过类比,写出在空间中的类似结论.ABCPpapbpcABCDP例1、试将平面上的圆与空间的球进行类比.圆的定义:平面内到一个定点的距离等于定长的点的集合.球的定义:到一个定点的距离等于定长的点的集合.圆
弦
直径周长
面积球
截面圆大圆表面积体积圆的概念和性质球的概念和性质与圆心距离相等的两弦相等与圆心距离不相等的两弦不相等,距圆心较近的弦较长以点(x0,y0)为圆心, r为半径的圆的方程为(x-x0)2+(y-y0)2 = r2圆心与弦(非直径)中点的连线垂直于弦球心与不过球心的截面(圆面)的圆点的连线垂直于截面与球心距离相等的两截面面积相等与球心距离不相等的两截面面积不相等,距球心较近的面积较大以点(x0,y0,z0)为球心, r为半径的球的方程为(x-x0)2+(y-y0)2+(z-z0)2 = r2利用圆的性质类比得出求的性质例题讲解c2 = a2+b2例3.有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
1.每次只能移动一个金属片;
2.较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?n=1时,n=2时,n=1时,n=3时,n=2时,n=1时,n=2时,n=1时,n=3时,n=4时,n=3时,n=2时,n=1时,古印度有一個傳說,婆羅賀摩(Brahma,眾生之父)在Berares地方的廟宇安置了一個含有64個金盤的婆羅賀摩塔,婆羅門教的憎侶們,奉命依遊戲規則要不停移動這些金盤,傳說中還說,當重排完成時,就是世界末日的到來,而經過計算,這64個金盤的遊戲至少要經過 264-1次才會完成,如果移動一次以1秒鐘計算,還要經過184467440737095551615天才能完成,照這樣看來,這世界還算蠻安全的。球心与截面圆(不是大圆)的圆点的连线垂直于截面圆与球心距离相等的两截面圆相等;与球心距离不等的两截面圆不等,距球心较近的截面圆较大球的切面垂直于过切点的半径;经过球心且垂直于切面的直线必经过切点经过切点且垂直于切面的直线必经过球心
