合情推理(一)[下学期]
图片预览








文档简介
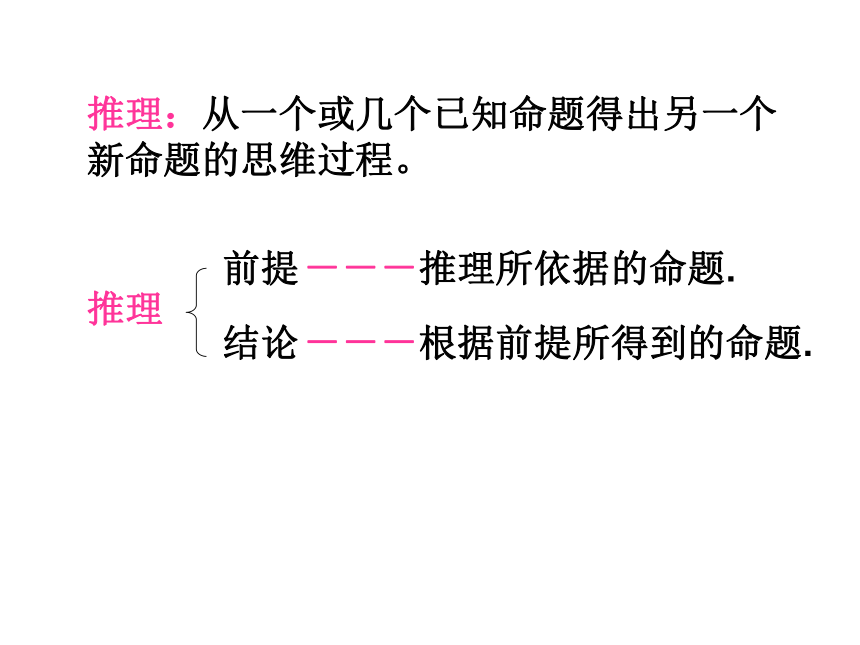
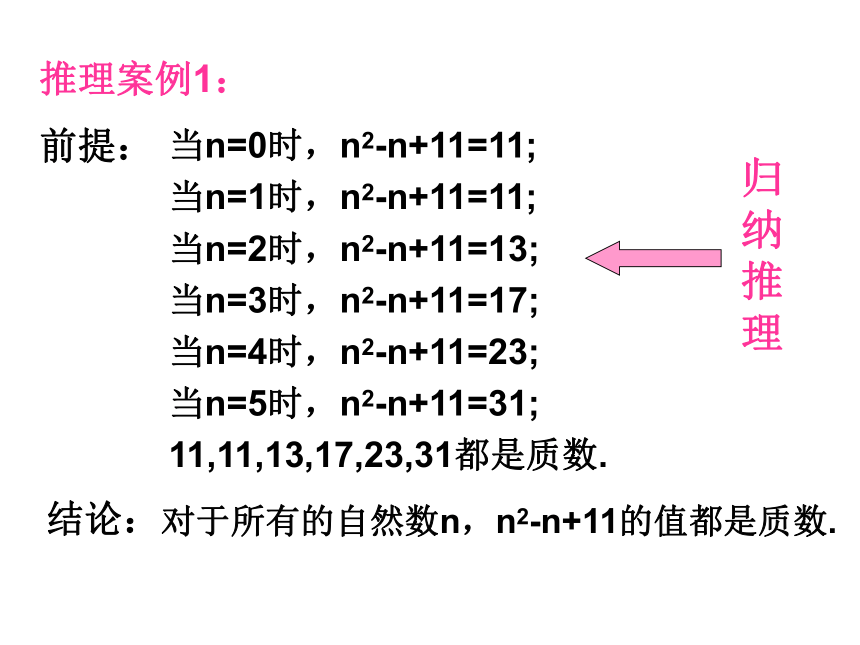
课件31张PPT。合情推理(1)推理:从一个或几个已知命题得出另一个新命题的思维过程。推理前提结论---推理所依据的命题.---根据前提所得到的命题.推理案例1:前提:当n=0时,n2-n+11=11;
当n=1时,n2-n+11=11;
当n=2时,n2-n+11=13;
当n=3时,n2-n+11=17;
当n=4时,n2-n+11=23;
当n=5时,n2-n+11=31;
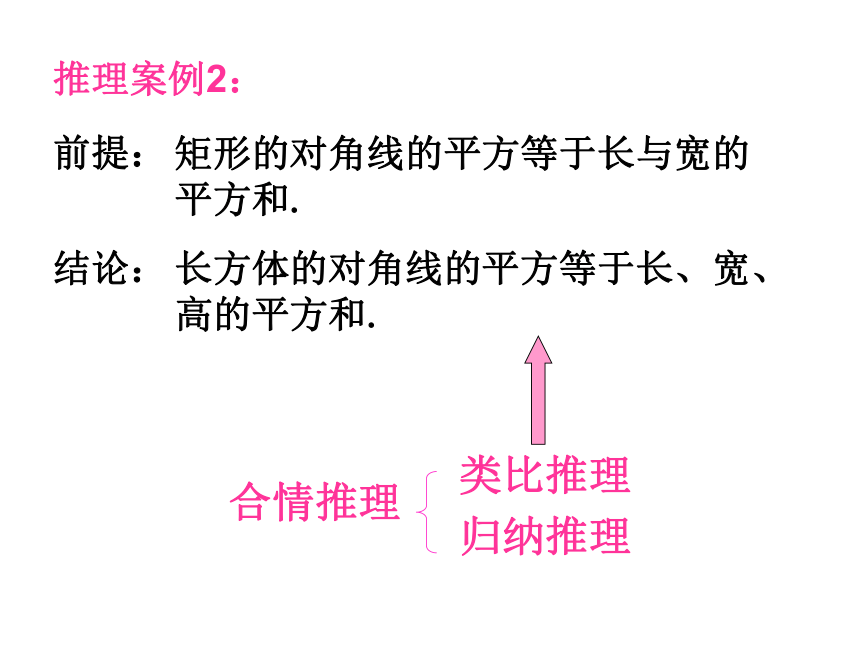
11,11,13,17,23,31都是质数.结论:对于所有的自然数n,n2-n+11的值都是质数.推理案例2:前提:结论:矩形的对角线的平方等于长与宽的平方和.长方体的对角线的平方等于长、宽、高的平方和.归纳推理例1:蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的。蛇、鳄鱼、海龟、蜥蜴都是爬行动物。由此猜想:例2:三角形的内角和是180度,凸四边形的内角和是360度,凸五边形的内角和是540度,……由此猜想:所有的爬行动物都是用肺呼吸的。凸n边形的内角和是(n-2) ×1800归纳推理例3:由此猜想:归纳推理的定义:归纳推理:概括、推广猜测一般性结论 简言之,归纳推理是由部分到整体、由个别到一般的推理。归纳推理的思维过程如下: 由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实推演出一般性的结论的推理,称为归纳推理(简称归纳).实验、观察构建数学:推理案例3:
金受热后体积膨胀,
银受热后体积膨胀,
铜受热后体积膨胀,
铁受热后体积膨胀,
金、银、铜、铁是金属的部分小类对象,它们受热后分子的凝聚力减弱,分子运动加速,分子彼此距离加大,从而导致体积膨胀
所以,所有的金属受热后都体积膨胀。再观察两个例子,你能得到归纳推理的一般模式吗?
推理案例4:磨擦双手(S1 )能产生热(P),
敲击石头(S2 )能产生热(P) ,
锤击铁块(S3 )能产生热(P) ,
磨擦双手、敲击石头、锤击铁块都是物质运动;
所以,物质运动能产生热。归纳推理的一般模式:S1具有P,S2具有P,……Sn具有P,(S1,S2,…,Sn是A类事物的对象)所以A类事物具有P1.归纳推理是依据特殊现象推断一般现象,因而,由归纳推理所得的结论超越了前提所包容的范围.2.归纳推理是依据若干已知的、没有穷尽的现象推断尚属未知的现象,因而结论具有猜测性.结论是否真实,还需经过逻辑证明和实践证明,因此它不能作为数学证明工具。3.归纳推理的前提是特殊的情况,因而归纳推理是立足于观察、经验和实验的基础之上.归纳推理是一种具有创造性的推理,通过归纳得到的猜想可作为进一步研究得起点,帮助人们发现问题和提出问题。归纳推理的几个特点:⑶ 检验猜想。⑵ 提出带有规律性的结论,即猜想;
⑴ 对有限的资料进行观察、分析、
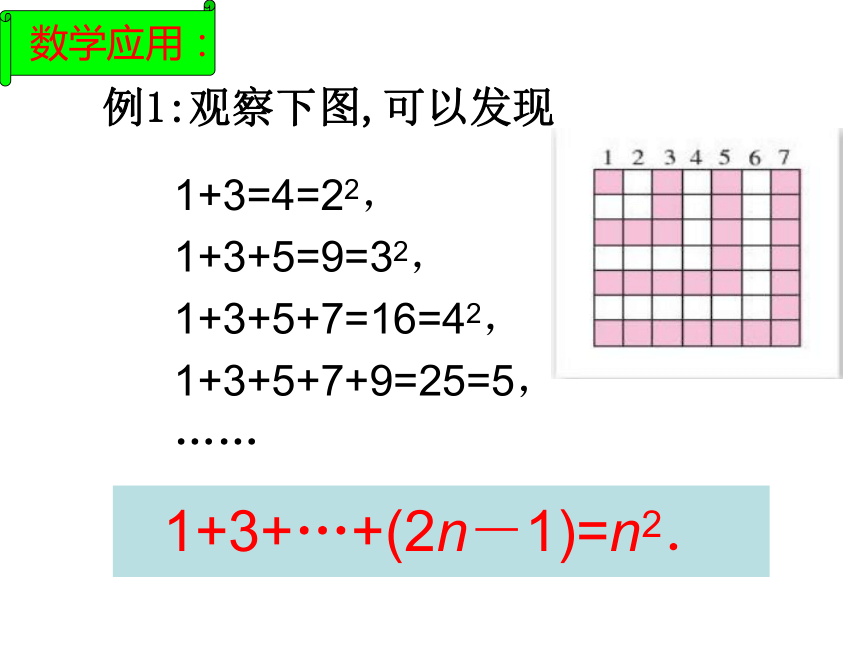
归纳整理;归纳推理的一般步骤:例1:观察下图,可以发现1+3+…+(2n-1)=n2.1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=5,
……
数学应用:例2:已知数列{an}的第1项a1=1且
(n=1,2,3 …),试归纳出这个数列的通项公式.例3:数一数图中的凸多面体的面数F、顶点数V和棱数E,然后用归纳法推理得出它们之间的关系.46455659846455659866861281261046455659866861281261077916910151015F+V-E=2猜想欧拉公式例4:如图有三根针和套在一根针上的若干金属片. 按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片; 2.较大的金属片不能放在较小的金属片上面.试推测;把n个金属片从1号针移到3号针,最少需要移动多少次?解;设an表示移动n块金属片时的移动次数.当n=1时,a1=1当n=2时,a2=3123当n=1时,a1=1当n=2时,a2=3解;设an表示移动n块金属片时的移动次数.当n=3时,a3=7当n=4时,a4=15猜想 an=2n -11231. 观察下列等式,并从中归纳出一般的结论:(1)数学巩固:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线。由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?2. 凸n边形有多少条对角线?3.在同一平面内,两条直线相交,有一个交点;三条直线相交,最多有几个交点?四条直线相交,最多有几个交点?……六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30, 歌德巴赫猜想:
“任何一个不小于6的偶数都等于两个奇质数之和”即:偶数=奇质数+奇质数改写为:10=3+7,20=3+17,30=13+17.6=3+3, 1000=29+971,
8=3+5, 1002=139+863,
10=5+5, …
12=5+7,
14=7+7,
16=5+11,
18 =7+11,
…, 数学阅读:四色猜想的提出来自英国。1852年,毕业于伦敦大学的弗南西
斯·格思里来到一家科研单位搞地图着色工作时,发现了一种有
趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共
同边界的国家着上不同的颜色。”这个结论能不能从数学上加以
严格证明呢?他和在大学读书的弟弟格里斯决心试一试。兄弟二
人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作
没有进展。
美国数学家富兰克林于1939年证明了22国以下的地图都可以
用四色着色。1950年,有人从22国推进到35国。1960年,有人又
证明了39国以下的地图可以只用四种颜色着色;随后又推进到了
50国。看来这种推进仍然十分缓慢。电子计算机问世以后,由于
演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜
想证明的进程。1976年,美国数学家阿佩尔与哈肯在美国伊利诺
斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿
判断,终于完成了四色定理的证明。四色猜想的计算机证明,轰
动了世界。它不仅解决了一个历时100多年的难题,而且有可能成
为数学史上一系列新思维的起点。不过也有不少数学家并不满足于
计算机取得的成就,他们还在寻找一种简捷明快的书面证明方法。
哥尼斯堡七桥问题
18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上
有7座桥,将河中的两个岛和河岸连结,如图1所示。 城中的
居民经常沿河过桥散步,于是提出了一个问题:能否一次走
遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。
这就是七桥问题,一个著名的图论问题。
当n=1时,n2-n+11=11;
当n=2时,n2-n+11=13;
当n=3时,n2-n+11=17;
当n=4时,n2-n+11=23;
当n=5时,n2-n+11=31;
11,11,13,17,23,31都是质数.结论:对于所有的自然数n,n2-n+11的值都是质数.推理案例2:前提:结论:矩形的对角线的平方等于长与宽的平方和.长方体的对角线的平方等于长、宽、高的平方和.归纳推理例1:蛇是用肺呼吸的,鳄鱼是用肺呼吸的,海龟是用肺呼吸的,蜥蜴是用肺呼吸的。蛇、鳄鱼、海龟、蜥蜴都是爬行动物。由此猜想:例2:三角形的内角和是180度,凸四边形的内角和是360度,凸五边形的内角和是540度,……由此猜想:所有的爬行动物都是用肺呼吸的。凸n边形的内角和是(n-2) ×1800归纳推理例3:由此猜想:归纳推理的定义:归纳推理:概括、推广猜测一般性结论 简言之,归纳推理是由部分到整体、由个别到一般的推理。归纳推理的思维过程如下: 由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实推演出一般性的结论的推理,称为归纳推理(简称归纳).实验、观察构建数学:推理案例3:
金受热后体积膨胀,
银受热后体积膨胀,
铜受热后体积膨胀,
铁受热后体积膨胀,
金、银、铜、铁是金属的部分小类对象,它们受热后分子的凝聚力减弱,分子运动加速,分子彼此距离加大,从而导致体积膨胀
所以,所有的金属受热后都体积膨胀。再观察两个例子,你能得到归纳推理的一般模式吗?
推理案例4:磨擦双手(S1 )能产生热(P),
敲击石头(S2 )能产生热(P) ,
锤击铁块(S3 )能产生热(P) ,
磨擦双手、敲击石头、锤击铁块都是物质运动;
所以,物质运动能产生热。归纳推理的一般模式:S1具有P,S2具有P,……Sn具有P,(S1,S2,…,Sn是A类事物的对象)所以A类事物具有P1.归纳推理是依据特殊现象推断一般现象,因而,由归纳推理所得的结论超越了前提所包容的范围.2.归纳推理是依据若干已知的、没有穷尽的现象推断尚属未知的现象,因而结论具有猜测性.结论是否真实,还需经过逻辑证明和实践证明,因此它不能作为数学证明工具。3.归纳推理的前提是特殊的情况,因而归纳推理是立足于观察、经验和实验的基础之上.归纳推理是一种具有创造性的推理,通过归纳得到的猜想可作为进一步研究得起点,帮助人们发现问题和提出问题。归纳推理的几个特点:⑶ 检验猜想。⑵ 提出带有规律性的结论,即猜想;
⑴ 对有限的资料进行观察、分析、
归纳整理;归纳推理的一般步骤:例1:观察下图,可以发现1+3+…+(2n-1)=n2.1+3=4=22,
1+3+5=9=32,
1+3+5+7=16=42,
1+3+5+7+9=25=5,
……
数学应用:例2:已知数列{an}的第1项a1=1且
(n=1,2,3 …),试归纳出这个数列的通项公式.例3:数一数图中的凸多面体的面数F、顶点数V和棱数E,然后用归纳法推理得出它们之间的关系.46455659846455659866861281261046455659866861281261077916910151015F+V-E=2猜想欧拉公式例4:如图有三根针和套在一根针上的若干金属片. 按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片; 2.较大的金属片不能放在较小的金属片上面.试推测;把n个金属片从1号针移到3号针,最少需要移动多少次?解;设an表示移动n块金属片时的移动次数.当n=1时,a1=1当n=2时,a2=3123当n=1时,a1=1当n=2时,a2=3解;设an表示移动n块金属片时的移动次数.当n=3时,a3=7当n=4时,a4=15猜想 an=2n -11231. 观察下列等式,并从中归纳出一般的结论:(1)数学巩固:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线。由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?2. 凸n边形有多少条对角线?3.在同一平面内,两条直线相交,有一个交点;三条直线相交,最多有几个交点?四条直线相交,最多有几个交点?……六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30, 歌德巴赫猜想:
“任何一个不小于6的偶数都等于两个奇质数之和”即:偶数=奇质数+奇质数改写为:10=3+7,20=3+17,30=13+17.6=3+3, 1000=29+971,
8=3+5, 1002=139+863,
10=5+5, …
12=5+7,
14=7+7,
16=5+11,
18 =7+11,
…, 数学阅读:四色猜想的提出来自英国。1852年,毕业于伦敦大学的弗南西
斯·格思里来到一家科研单位搞地图着色工作时,发现了一种有
趣的现象:“看来,每幅地图都可以用四种颜色着色,使得有共
同边界的国家着上不同的颜色。”这个结论能不能从数学上加以
严格证明呢?他和在大学读书的弟弟格里斯决心试一试。兄弟二
人为证明这一问题而使用的稿纸已经堆了一大叠,可是研究工作
没有进展。
美国数学家富兰克林于1939年证明了22国以下的地图都可以
用四色着色。1950年,有人从22国推进到35国。1960年,有人又
证明了39国以下的地图可以只用四种颜色着色;随后又推进到了
50国。看来这种推进仍然十分缓慢。电子计算机问世以后,由于
演算速度迅速提高,加之人机对话的出现,大大加快了对四色猜
想证明的进程。1976年,美国数学家阿佩尔与哈肯在美国伊利诺
斯大学的两台不同的电子计算机上,用了1200个小时,作了100亿
判断,终于完成了四色定理的证明。四色猜想的计算机证明,轰
动了世界。它不仅解决了一个历时100多年的难题,而且有可能成
为数学史上一系列新思维的起点。不过也有不少数学家并不满足于
计算机取得的成就,他们还在寻找一种简捷明快的书面证明方法。
哥尼斯堡七桥问题
18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上
有7座桥,将河中的两个岛和河岸连结,如图1所示。 城中的
居民经常沿河过桥散步,于是提出了一个问题:能否一次走
遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。
这就是七桥问题,一个著名的图论问题。
