2.1.2演绎推理.[下学期]
文档属性
| 名称 | 2.1.2演绎推理.[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 208.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-10 00:00:00 | ||
图片预览







文档简介
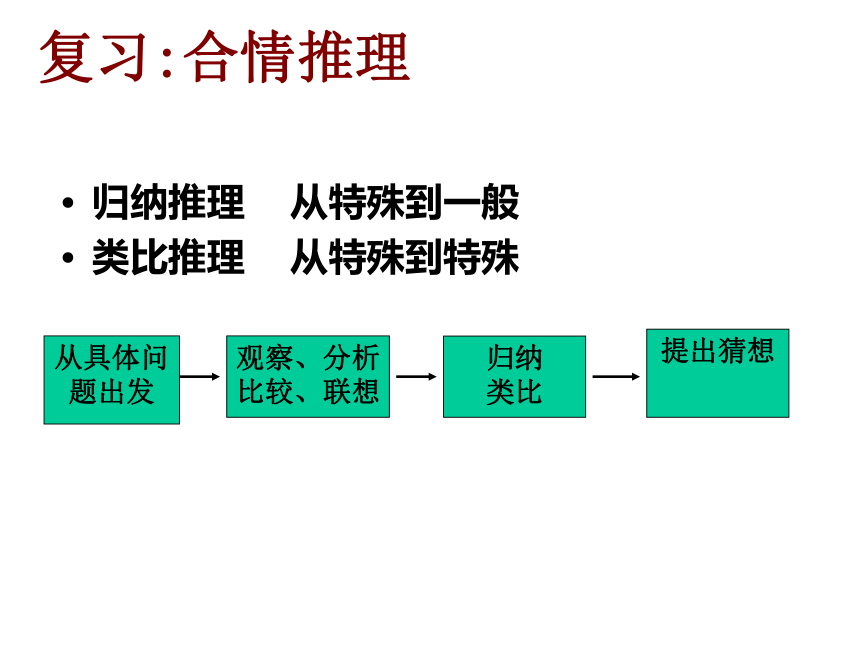
课件21张PPT。复习:合情推理归纳推理 从特殊到一般
类比推理 从特殊到特殊从具体问题出发观察、分析
比较、联想提出猜想归纳
类比小明是一名高二年级的学生,17岁,迷恋上网络,沉迷于虚拟的世界当中。由于每月的零花钱不够用,便向亲戚要钱,但这仍然满足不了需求,于是就产生了歹念,强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元,这应该不会很严重吧???
如果你是法官,你会如何判决呢?小明到底是不是犯罪呢?情景创设1:生活中的例子情景创设2 观察与思考1.所有的金属都能导电, 2.一切奇数都不能被2整除, 3.三角函数都是周期函数, 铜能够导电.铜是金属, (2100+1)不能被2整除.(2100+1)是奇数, tan 周期函数 tan 三角函数,是合情推理吗?1.所有的金属都能导电, 2.一切奇数都不能被2整除, 3.三角函数都是周期函数, 4.全等的三角形面积相等 所以铜能够导电.因为铜是金属, 所以(2100+1)不能被2整除.因为(2100+1)是奇数,因为tan 三角函数,那么三角形ABC与三角形A1B1C1面积相等.如果三角形ABC与三角形A1B1C1全等,情景创设2:观察下列推理有什么特点?所以是tan 周期函数 从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.一、演绎推理的定义:二、演绎推理的模式:“三段论”是演绎推理的一般模式;M……P(M是P)S……M (S是M)S……P (S是P)大前提---已知的一般原理;小前提---所研究的特殊对象; 结论---据一般原理,对特殊
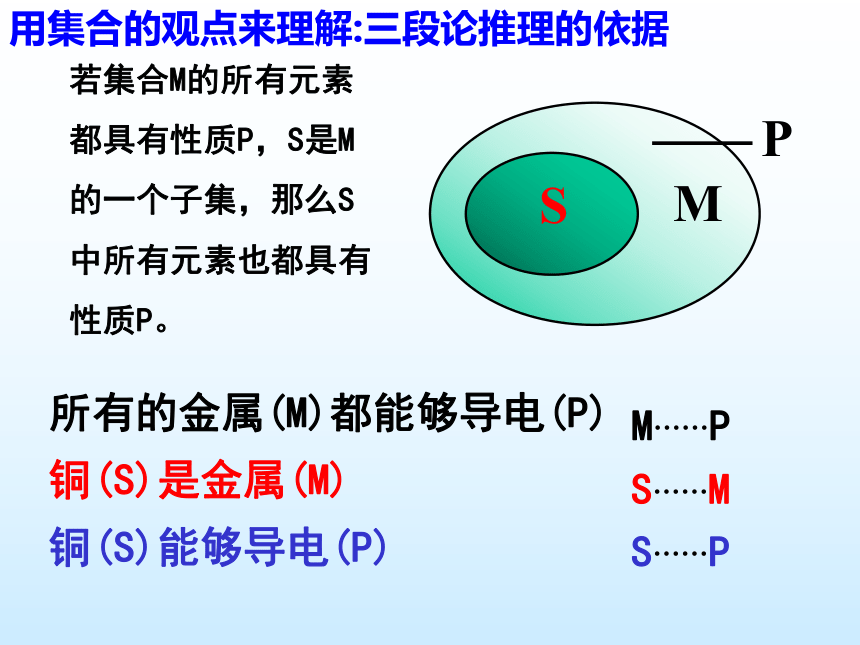
对象做出的判断.若集合M的所有元素
都具有性质P,S是M
的一个子集,那么S
中所有元素也都具有
性质P。所有的金属(M)都能够导电(P)
铜(S)是金属(M)
铜(S)能够导电(P)M……PS……MS……P用集合的观点来理解:三段论推理的依据 大前提:刑法规定抢劫罪是以非法占有为目的,使用暴力、胁迫或其他方法,强行劫取公私财物的行为。其刑事责任年龄起点为14周岁,对财物的数额没有要求。小前提:小明超过14周岁,强行向路人抢取钱财50元。结论:小明犯了抢劫罪。小明是一名高二年级的学生,17岁,迷恋上网络,沉迷于虚拟的世界当中。由于每月的零花钱不够用,便向亲戚要钱,但这仍然满足不了需求,于是就产生了歹念,强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元,这应该不会很严重吧??练习3:证明函数f(x)=-x2+2x在(-∞,1]上是增函数.满足对于任意x1,x2∈D,若x1f(x1)-f(x2)=(-x12+2x1)-(x22+2x2)
=(x2-x1)(x1+x2-2) 因为x10
因为x1,x2≤1所以x1+x2-2<0
因此f(x1)-f(x2)<0,即f(x1)(1)因为指数函数 是增函数,
而 是指数函数,
所以 是增函数。错因:大前提是错误的,所以结论是错误的。思考、演绎推理的结论一定正确吗?三、演绎推理的特点:1.演绎推理的前提是一般性原理,演绎所得的的结论是蕴含于前提之中的个别、特殊事实,结论完全蕴含于前提之中,因此演绎推理是由一般到特殊的推理;
2、在演绎推理中,前提于结论之间存在着必然的联系,只要前提和推理形式是正确的,结论必定正确。因此演绎推理是数学中严格的证明工具。3、在演绎推理是一种收敛性的思维方法,它较少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学论证和系统化。四、合情推理与演绎推理的区别合情推理归纳推理类比推理由部分到整体、个
别到一般的推理。由特殊到特殊
的推理。 结论不一定正确,有待进一
步证明。演绎推理由一般到特殊的
推理。在大前提、小前提
和推理形式都正确
的前提下,得到的
结论一定正确。 合情推理的结论需要演绎推理的验证,而演绎
推理的方向和思路一般是通过合情推理获得的。练习(优化设计)P68~~~~1,2,3
P69~~~~4,1,4,5,9练习1、下面说法正确的有( )
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个 B、2个 C、3个 D、4个C补充练习练习2:用三段论的形式写出下列演绎推理。
(1)三角形内角和180°,等边三角形内
角和是180°。
(1)分析:省略了小前提:“等边三角形是三角形”。(2) 是有理数。(2)分析:省略了大前提:“所有的循环小数都是有理数。” 小前提: 是循环小数。解:三角形内角和180°,所以等边三角形内角和是180°。等边三角形是三角形。练习3. 指出下列推理中的错误,并分析产生错误的原因;(1)整数是自然数,-3是整数,-3是自然数;(2)无理数是无限小数,是无限小数,是无理数.大前提 错误练习.在锐角三角形ABC中,AD⊥BC, BE⊥AC,D,E是垂足,用演绎推理“三段论”格式证AB的中点M到D,E的距离相等. (1)因为有一个内角是只直角的三角形是直角三角形,在△ABC中,AD⊥BC,即∠ADB=900所以△ABD是直角三角形同理△ABE是直角三角形(2)因为直角三角形斜边上的中线等于斜边的一半,M是Rt△ABD斜边AB的中点,DM是斜边上的中线所以 DM= AB同理 EM= AB所以 DM = EM大前提小前提结论大前提小前提结论证明:例4:已知a,b,m均为正实数,b0,所以mb0,(大前提)(小前提)(大前提)(小前提)(大前提)(小前提)(结论)(结论)(结论)演绎推理概念
一般形式——三段论
证明问题
合情推理与演绎推理的联系与区别(难点)(重点)(重点)四、小结大前提小前提结论2007不能被2整除冥王星以椭圆形轨道绕太阳运行铜能导电注 演绎推理有时可用列表的形式表示,如:学习目标:
1、什么是演绎推理?
2、什么是三段论?
3、合情推理与演绎推理有哪些区别?
4、能举出一些在生活和学习中有关演绎
推理的例子。三、新课
类比推理 从特殊到特殊从具体问题出发观察、分析
比较、联想提出猜想归纳
类比小明是一名高二年级的学生,17岁,迷恋上网络,沉迷于虚拟的世界当中。由于每月的零花钱不够用,便向亲戚要钱,但这仍然满足不了需求,于是就产生了歹念,强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元,这应该不会很严重吧???
如果你是法官,你会如何判决呢?小明到底是不是犯罪呢?情景创设1:生活中的例子情景创设2 观察与思考1.所有的金属都能导电, 2.一切奇数都不能被2整除, 3.三角函数都是周期函数, 铜能够导电.铜是金属, (2100+1)不能被2整除.(2100+1)是奇数, tan 周期函数 tan 三角函数,是合情推理吗?1.所有的金属都能导电, 2.一切奇数都不能被2整除, 3.三角函数都是周期函数, 4.全等的三角形面积相等 所以铜能够导电.因为铜是金属, 所以(2100+1)不能被2整除.因为(2100+1)是奇数,因为tan 三角函数,那么三角形ABC与三角形A1B1C1面积相等.如果三角形ABC与三角形A1B1C1全等,情景创设2:观察下列推理有什么特点?所以是tan 周期函数 从一般性的原理出发,推出某个特殊情况下的结论,这种推理称为演绎推理.一、演绎推理的定义:二、演绎推理的模式:“三段论”是演绎推理的一般模式;M……P(M是P)S……M (S是M)S……P (S是P)大前提---已知的一般原理;小前提---所研究的特殊对象; 结论---据一般原理,对特殊
对象做出的判断.若集合M的所有元素
都具有性质P,S是M
的一个子集,那么S
中所有元素也都具有
性质P。所有的金属(M)都能够导电(P)
铜(S)是金属(M)
铜(S)能够导电(P)M……PS……MS……P用集合的观点来理解:三段论推理的依据 大前提:刑法规定抢劫罪是以非法占有为目的,使用暴力、胁迫或其他方法,强行劫取公私财物的行为。其刑事责任年龄起点为14周岁,对财物的数额没有要求。小前提:小明超过14周岁,强行向路人抢取钱财50元。结论:小明犯了抢劫罪。小明是一名高二年级的学生,17岁,迷恋上网络,沉迷于虚拟的世界当中。由于每月的零花钱不够用,便向亲戚要钱,但这仍然满足不了需求,于是就产生了歹念,强行向路人抢取钱财。但小明却说我是未成年人而且就抢了50元,这应该不会很严重吧??练习3:证明函数f(x)=-x2+2x在(-∞,1]上是增函数.满足对于任意x1,x2∈D,若x1
=(x2-x1)(x1+x2-2) 因为x1
因为x1,x2≤1所以x1+x2-2<0
因此f(x1)-f(x2)<0,即f(x1)
而 是指数函数,
所以 是增函数。错因:大前提是错误的,所以结论是错误的。思考、演绎推理的结论一定正确吗?三、演绎推理的特点:1.演绎推理的前提是一般性原理,演绎所得的的结论是蕴含于前提之中的个别、特殊事实,结论完全蕴含于前提之中,因此演绎推理是由一般到特殊的推理;
2、在演绎推理中,前提于结论之间存在着必然的联系,只要前提和推理形式是正确的,结论必定正确。因此演绎推理是数学中严格的证明工具。3、在演绎推理是一种收敛性的思维方法,它较少创造性,但却具有条理清晰、令人信服的论证作用,有助于科学论证和系统化。四、合情推理与演绎推理的区别合情推理归纳推理类比推理由部分到整体、个
别到一般的推理。由特殊到特殊
的推理。 结论不一定正确,有待进一
步证明。演绎推理由一般到特殊的
推理。在大前提、小前提
和推理形式都正确
的前提下,得到的
结论一定正确。 合情推理的结论需要演绎推理的验证,而演绎
推理的方向和思路一般是通过合情推理获得的。练习(优化设计)P68~~~~1,2,3
P69~~~~4,1,4,5,9练习1、下面说法正确的有( )
(1)演绎推理是由一般到特殊的推理;
(2)演绎推理得到的结论一定是正确的;
(3)演绎推理一般模式是“三段论”形式;
(4)演绎推理的结论的正误与大前提、小前提和推理形式有关。
A、1个 B、2个 C、3个 D、4个C补充练习练习2:用三段论的形式写出下列演绎推理。
(1)三角形内角和180°,等边三角形内
角和是180°。
(1)分析:省略了小前提:“等边三角形是三角形”。(2) 是有理数。(2)分析:省略了大前提:“所有的循环小数都是有理数。” 小前提: 是循环小数。解:三角形内角和180°,所以等边三角形内角和是180°。等边三角形是三角形。练习3. 指出下列推理中的错误,并分析产生错误的原因;(1)整数是自然数,-3是整数,-3是自然数;(2)无理数是无限小数,是无限小数,是无理数.大前提 错误练习.在锐角三角形ABC中,AD⊥BC, BE⊥AC,D,E是垂足,用演绎推理“三段论”格式证AB的中点M到D,E的距离相等. (1)因为有一个内角是只直角的三角形是直角三角形,在△ABC中,AD⊥BC,即∠ADB=900所以△ABD是直角三角形同理△ABE是直角三角形(2)因为直角三角形斜边上的中线等于斜边的一半,M是Rt△ABD斜边AB的中点,DM是斜边上的中线所以 DM= AB同理 EM= AB所以 DM = EM大前提小前提结论大前提小前提结论证明:例4:已知a,b,m均为正实数,b
一般形式——三段论
证明问题
合情推理与演绎推理的联系与区别(难点)(重点)(重点)四、小结大前提小前提结论2007不能被2整除冥王星以椭圆形轨道绕太阳运行铜能导电注 演绎推理有时可用列表的形式表示,如:学习目标:
1、什么是演绎推理?
2、什么是三段论?
3、合情推理与演绎推理有哪些区别?
4、能举出一些在生活和学习中有关演绎
推理的例子。三、新课
