2.2.2间接证明(反证法)[下学期]
文档属性
| 名称 | 2.2.2间接证明(反证法)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 78.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-02-09 12:55:00 | ||
图片预览





文档简介
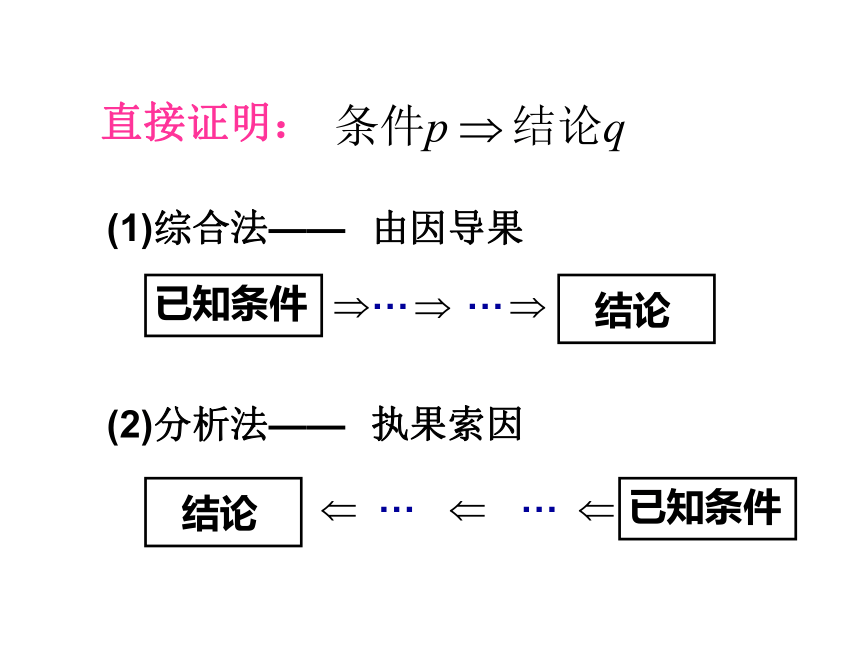
课件13张PPT。2.2.2 间接证明南京市南湖高级中学高二数学备课组苏教版◎选修1-2直接证明:(1)综合法——(2)分析法——由因导果执果索因 A、B、C三个人,A说B撒谎,B说C撒谎,C说A、B都撒谎。则C必定是在撒谎,为什么?分析:假设C没有撒谎, 则C真. - - 那么A假且B假;由A假, 知B真. 这与B假矛盾.那么假设C没有撒谎不成立,则C必定是在撒谎.引例1: 将9个球分别染成红色或白色。那么无论怎样染,至少有5个球是同色的。你能证明这个结论吗?引例2:间接证明: 不是直接从原命题的条件逐步推得命题成立的证明方法。反证法是一种常用的间接证明的方法。 一般地,假设原命题不成立, 经过正确的推理,最后得出矛盾。 因此说明假设错误,从而证明了原命题成立, 这样的证明方法叫做反证法(归谬法)。其过程包括:反设——假设命题的结论不成立;存真——由矛盾结果,断定反设不真,从而肯定原结论成立。归谬——从假设出发,经过一系列正确的推理,得出矛盾;??归缪矛盾:
(1)与已知条件矛盾;
(2)与已有公理、定理、定义矛盾;
(3)自相矛盾。例1、已知:一个整数的平方能被2整除,
求证:这个数是偶数。证明:假设a不是偶数,
则a是奇数,不妨设a=2m+1(m是整数)
∴a2=(2m+1)2=4m2+4m+1=4m(m+1)+1
∴a2是奇数,与已知矛盾。
∴假设不成立,所以a是偶数。例2、用反证法证明:
如果a>b>0,那么例3、已知a≠0,求证关于x的方程ax=b有且只有一个根。例4、求证:圆的两条不全是直径的相交弦不能互相平分.已知:在⊙O中,弦AB、CD相交于P,且AB、CD不全是直径 求证:AB、CD不能互相平分。ABCD 例5、求证: 是无理数。 (4)结论为 “唯一”类的命题。正难则反!应用反证法的情形: (1)直接证明困难;(2)需分成很多类进行讨论;(3)结论为“至少”、“至多”、“有无穷多个”
这一类的命题;推理 合情推理 演绎推理
(归纳、类比) (三段论)证明 直接证明 间接证明
(分析法、综合法) (反证法)数学—公理化思想
(1)与已知条件矛盾;
(2)与已有公理、定理、定义矛盾;
(3)自相矛盾。例1、已知:一个整数的平方能被2整除,
求证:这个数是偶数。证明:假设a不是偶数,
则a是奇数,不妨设a=2m+1(m是整数)
∴a2=(2m+1)2=4m2+4m+1=4m(m+1)+1
∴a2是奇数,与已知矛盾。
∴假设不成立,所以a是偶数。例2、用反证法证明:
如果a>b>0,那么例3、已知a≠0,求证关于x的方程ax=b有且只有一个根。例4、求证:圆的两条不全是直径的相交弦不能互相平分.已知:在⊙O中,弦AB、CD相交于P,且AB、CD不全是直径 求证:AB、CD不能互相平分。ABCD 例5、求证: 是无理数。 (4)结论为 “唯一”类的命题。正难则反!应用反证法的情形: (1)直接证明困难;(2)需分成很多类进行讨论;(3)结论为“至少”、“至多”、“有无穷多个”
这一类的命题;推理 合情推理 演绎推理
(归纳、类比) (三段论)证明 直接证明 间接证明
(分析法、综合法) (反证法)数学—公理化思想
