推理与证明[下学期]
图片预览










文档简介
课件34张PPT。系列1&系列2选修1-1:常用逻辑用语 圆锥曲线与方程 导数及其应用
选修1-2:统计案例 推理与证明 数系的扩充与复数的引入 框图
选修2-1:常用逻辑用语 圆锥曲线与方程 空间中的向量与立体几何
选修2-2:导数及其应用 推理与证明 数系的扩充与复数的引入
选修2-3:计数原理 统计案例 概率
普通高中课程标准实验教科书
选修 · 推理与证明
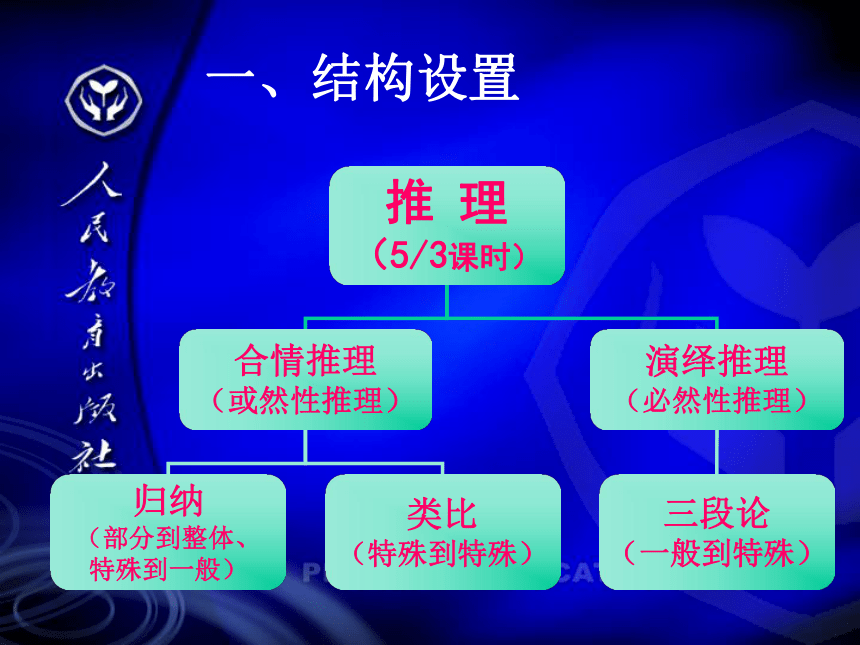
简 介人民教育出版社中学数学室 宋莉莉 一、结构设置二、教学目标1.了解合情推理和演绎推理的含义。
2.能正确地运用合情推理和演绎推理进行简单的推理。
3.了解合情推理与演绎推理之间的联系与差别。
4.了解直接证明的两种基本方法——分析法和综合法的思考过程、特点。
5.了解间接证明的一种基本方法──反证法的思考过程、特点。
6.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
2.以变分散为集中,变隐性为显性的方式讲推理和证明,并给出了推理和证明的一般定义。
3.用流程图描绘推理和证明过程。 归纳推理的定义
3+7=10,3+17=20,13+17=30,
10=3+7,20=3+17,30=13+17.
偶数=奇质数+奇质数
6=3+3,8=3+5,10=5+5,12=5+7,14=7+7,
16=5+11,…, 1 000=29+971,…
⑴ 一个偶数(不小于6)总可以表示成两个奇质数之和;
⑵ 没有发现反例 。四、主要内容的编写特点和教学建议归纳推理的一般步骤:⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想;
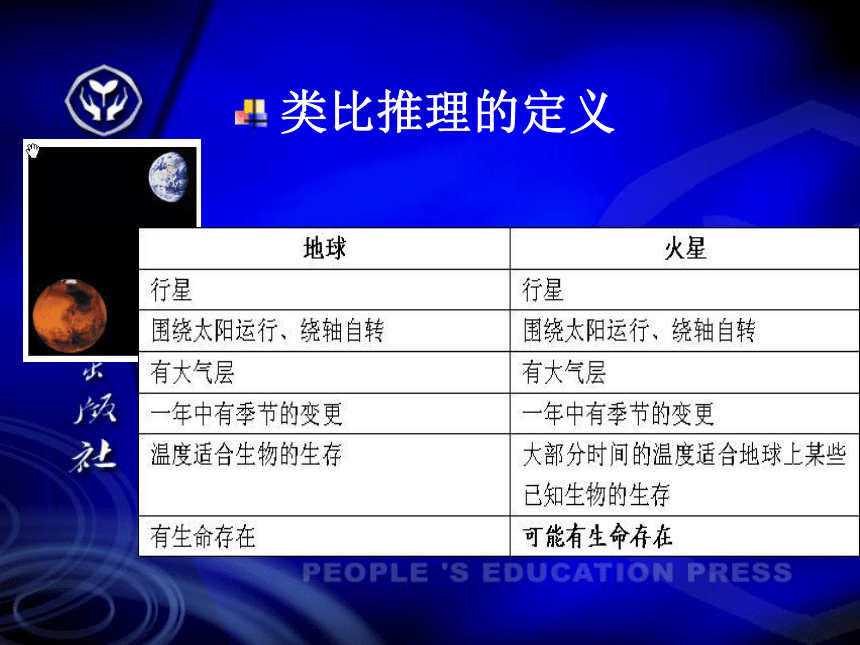
⑶ 检验猜想。 类比推理的定义
这种由两类对象具有某些类似特征,和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比).简言之,类比推理是由特殊到特殊的推理.类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
⑶ 检验猜想。 类比推理举例可以从不同角度确定类比对象:构成几何体的元素数目:四面体 三角形 类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想. 演绎推理举例证明函数 f(x)=-x2+2x 在(-∞,1]上是增函数. 分析:证明本例所依据的大前提是增函数的定义,即函数y=f(x)满足在给定区间内任取自变量的两个值x1,x2,若x1<x2,则有f(x1)<f(x2).
小前提是f(x)=-x2+2x,x∈(-∞,1]满足增函数的定义,这是证明本例的关键. 纠正典型错误⑴ 合情推理的结论不一定正确
费马猜想:任何形如 (n∈N*)的数都是质数.
反例: ⑵ 演绎推理的形式正确,大前提错误,结论也是错误的 合情推理和演绎推理的区别 与联系推理形式:归纳是由部分到整体、个别到一般的推理,类比是由特殊到特殊的推理;而演绎推理是由一般到特殊的推理。
推理所得的结论:合情推理的结论不一定正确,有待进一步证明;演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得的。 综合法定义
1.回忆、描述
在数学证明中,我们经常从已知条件和某些学过的定义、定理、公理等出发,通过推理推导出所要的结论.
2.举例、体验特点
分析法定义
1.回忆、描述
在数学证明中,我们还经常从要证的结论出发,反推回去,寻求保证结论成立的条件,直到找到一个明显成立的条件为止.
2.举例、体验特点
3.定义 一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
“两头挤” 把分析法和综合法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间条件P.若由P可以推出Q成立,就可以证明结论成立.
反证法1.反证法的特点:
假设原结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.
2.应用反证法的情形:
直接证明难找到证明思路(例题)、需分成很多类进行讨论(引例). 数学归纳法1.数学归纳法是一种特殊的证明方法,主要用于证明与正整数有关的数学命题。
特点:通过有限个步骤的推理,证明n取无限多个正整数的情形.
2. 数学归纳法的原理:使“多米诺骨牌”全部倒下的两个条件:
⑴ 第一块骨牌倒下;
⑵ 任意相邻的两块骨牌,前一块倒下一定导 致后一块倒下.
两个条件的作用:
条件⑴:奠基;条件⑵:递推关系
数学归纳法的原理:
⑴(归纳奠基):命题对n=n0成立(n0为使猜想成立的最小的正整数);
⑵(归纳递推):命题若对n=k成立,则对k+1也成立(k≥n0).
第二步学生普遍存在的问题:为什么能在假设下进行证明?
五.需要注意的问题推理教学的重点在于通过具体实例理解合情推理和演绎推理,而不追求对概念的抽象表述。
证明的教学应引导学生认识各种证明方法的特点,体会证明的必要性,对证明的技巧性不宜作过高的要求。
讲清楚数学归纳法证明的原理,要控制难度——证明简单的数学命题。
文理差异
选修1-2:统计案例 推理与证明 数系的扩充与复数的引入 框图
选修2-1:常用逻辑用语 圆锥曲线与方程 空间中的向量与立体几何
选修2-2:导数及其应用 推理与证明 数系的扩充与复数的引入
选修2-3:计数原理 统计案例 概率
普通高中课程标准实验教科书
选修 · 推理与证明
简 介人民教育出版社中学数学室 宋莉莉 一、结构设置二、教学目标1.了解合情推理和演绎推理的含义。
2.能正确地运用合情推理和演绎推理进行简单的推理。
3.了解合情推理与演绎推理之间的联系与差别。
4.了解直接证明的两种基本方法——分析法和综合法的思考过程、特点。
5.了解间接证明的一种基本方法──反证法的思考过程、特点。
6.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题。
2.以变分散为集中,变隐性为显性的方式讲推理和证明,并给出了推理和证明的一般定义。
3.用流程图描绘推理和证明过程。 归纳推理的定义
3+7=10,3+17=20,13+17=30,
10=3+7,20=3+17,30=13+17.
偶数=奇质数+奇质数
6=3+3,8=3+5,10=5+5,12=5+7,14=7+7,
16=5+11,…, 1 000=29+971,…
⑴ 一个偶数(不小于6)总可以表示成两个奇质数之和;
⑵ 没有发现反例 。四、主要内容的编写特点和教学建议归纳推理的一般步骤:⑴ 对有限的资料进行观察、分析、归纳 整理;
⑵ 提出带有规律性的结论,即猜想;
⑶ 检验猜想。 类比推理的定义
这种由两类对象具有某些类似特征,和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理(简称类比).简言之,类比推理是由特殊到特殊的推理.类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;
⑵ 用一类对象的已知特征去推测另一类对象的特征,从而得出一个猜想;
⑶ 检验猜想。 类比推理举例可以从不同角度确定类比对象:构成几何体的元素数目:四面体 三角形 类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想. 演绎推理举例证明函数 f(x)=-x2+2x 在(-∞,1]上是增函数. 分析:证明本例所依据的大前提是增函数的定义,即函数y=f(x)满足在给定区间内任取自变量的两个值x1,x2,若x1<x2,则有f(x1)<f(x2).
小前提是f(x)=-x2+2x,x∈(-∞,1]满足增函数的定义,这是证明本例的关键. 纠正典型错误⑴ 合情推理的结论不一定正确
费马猜想:任何形如 (n∈N*)的数都是质数.
反例: ⑵ 演绎推理的形式正确,大前提错误,结论也是错误的 合情推理和演绎推理的区别 与联系推理形式:归纳是由部分到整体、个别到一般的推理,类比是由特殊到特殊的推理;而演绎推理是由一般到特殊的推理。
推理所得的结论:合情推理的结论不一定正确,有待进一步证明;演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确。
合情推理的结论需要演绎推理的验证,而演绎推理的内容一般是通过合情推理获得的。 综合法定义
1.回忆、描述
在数学证明中,我们经常从已知条件和某些学过的定义、定理、公理等出发,通过推理推导出所要的结论.
2.举例、体验特点
分析法定义
1.回忆、描述
在数学证明中,我们还经常从要证的结论出发,反推回去,寻求保证结论成立的条件,直到找到一个明显成立的条件为止.
2.举例、体验特点
3.定义 一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
“两头挤” 把分析法和综合法结合起来使用:根据条件的结构特点去转化结论,得到中间结论Q;根据结论的结构特点去转化条件,得到中间条件P.若由P可以推出Q成立,就可以证明结论成立.
反证法1.反证法的特点:
假设原结论不成立,经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明了原命题成立.
2.应用反证法的情形:
直接证明难找到证明思路(例题)、需分成很多类进行讨论(引例). 数学归纳法1.数学归纳法是一种特殊的证明方法,主要用于证明与正整数有关的数学命题。
特点:通过有限个步骤的推理,证明n取无限多个正整数的情形.
2. 数学归纳法的原理:使“多米诺骨牌”全部倒下的两个条件:
⑴ 第一块骨牌倒下;
⑵ 任意相邻的两块骨牌,前一块倒下一定导 致后一块倒下.
两个条件的作用:
条件⑴:奠基;条件⑵:递推关系
数学归纳法的原理:
⑴(归纳奠基):命题对n=n0成立(n0为使猜想成立的最小的正整数);
⑵(归纳递推):命题若对n=k成立,则对k+1也成立(k≥n0).
第二步学生普遍存在的问题:为什么能在假设下进行证明?
五.需要注意的问题推理教学的重点在于通过具体实例理解合情推理和演绎推理,而不追求对概念的抽象表述。
证明的教学应引导学生认识各种证明方法的特点,体会证明的必要性,对证明的技巧性不宜作过高的要求。
讲清楚数学归纳法证明的原理,要控制难度——证明简单的数学命题。
文理差异
