导数的几何意义[上学期]
图片预览






文档简介
(共25张PPT)
导数的几何意义1
先来复习导数的概念
1.函数的平均变化率
2、 t0时刻的瞬时速度
如果函数y=f(x)在点x=x0存在导数,就说函数y=f(x)在点x0处可导,如果极限不存在,就说函数 f(x)在点x0处不可导.
由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:
注意:
这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.
β
y=f(x)
P
Q
M
Δx
Δy
O
x
y
β
P
y=f(x)
Q
M
Δx
Δy
O
x
y
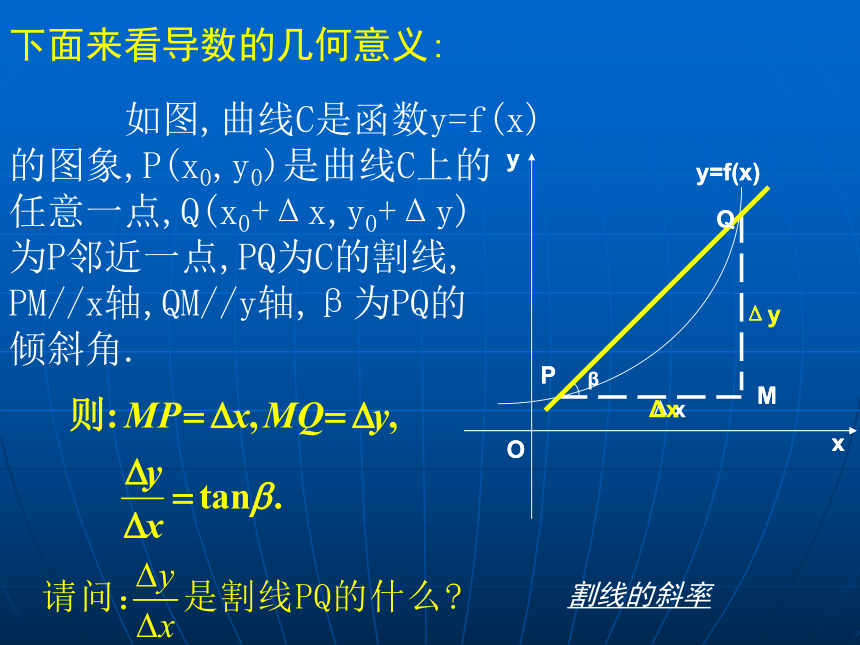
如图,曲线C是函数y=f(x)
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
倾斜角.
下面来看导数的几何意义:
割线的斜率
P
Q
o
x
y
y=f(x)
割线
切线
T
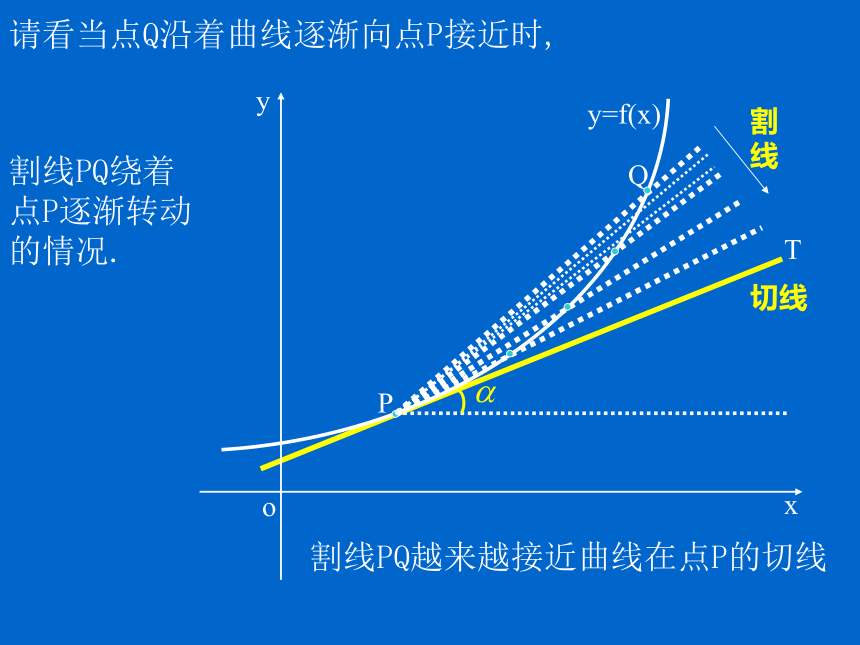
请看当点Q沿着曲线逐渐向点P接近时,
割线PQ绕着
点P逐渐转动
的情况.
割线PQ越来越接近曲线在点P的切线
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.
设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.
即:
这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数在x=x0处的导数.
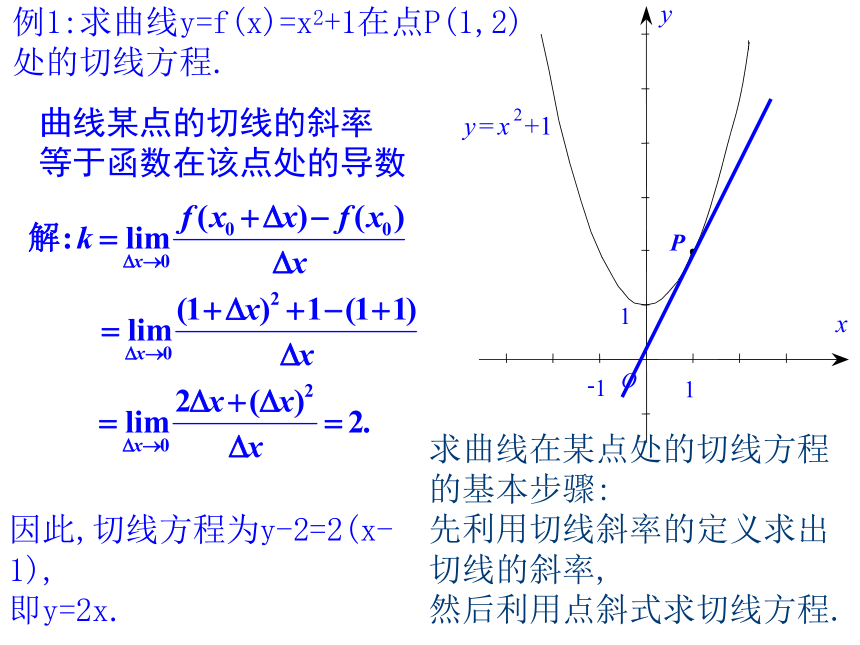
例1:求曲线y=f(x)=x2+1在点P(1,2)
处的切线方程.
P
y
=
x
2
+1
x
y
-
1
1
1
O
因此,切线方程为y-2=2(x-1),
即y=2x.
求曲线在某点处的切线方程
的基本步骤:
先利用切线斜率的定义求出切线的斜率,
然后利用点斜式求切线方程.
曲线某点的切线的斜率
等于函数在该点处的导数
练习:如图已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.
y
x
-2
-1
1
2
-2
-1
1
2
3
4
O
P
即点P处的切线的斜率等于4.
(2)在点P处的切线方程是y-8/3=4(x-2),
即12x-3y-16=0.
(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。
(2)根据直线方程的点斜式写出切线方程,即
d.求切线方程的步骤:
例:求过点P(3,5)且与曲线y=x2相切的直线方程.
说明:曲线上求在点P处的切线与求过点P的切线有区别.
在点P处的切线,点P必为切点,求过点P的切线,点P
未必是切点.应注意概念的区别,其求法也有所不同.
解:设所求切线的切点在A(x0,y0).
因为A是曲线y=x2上的一点,所以,y0=x02 ①.
又因为函数y=x2的导数为 所以过点A(x0,y0)的
切线的斜率为
由于所求切线过P(3,5)和A(x0,y0)两点,故其斜率又
应为 ②.
联立①,②解得:
故切点分别为(1,1)或(5,25).
当切点为(1,1)时,切线的斜率为k1=2x0=2;
当切点为(5,25)时,切线的斜率为k2=2x0=10;
所以所求的切线有两条,方程分别为:y-1=2(x-1)或y-25=10(x-5),即y=2x-1或y=10x-25.
某时刻血管中药物的浓度的瞬间变化率,
即等于函数图像上该点处的切线的斜率
小结:
函数在某处的导数的几何意义:
函数图像上该点处的切线的斜率
1、用途1:求解曲线上某点的切线方程
2:求过点P(8,-3)且与曲线y=1/x相切的直线方程.
1、已知曲线 f(x)=3x2+x-1上的一点P,横坐标为-2,
求:(1)点P处的切线的斜率; (2)点P处的切线方程.
作业
P11;T4
导数的几何意义2
函数在某处的导数的几何意义:
朝花夕拾
函数在某处的导数值等于函数图像上
该点处的切线的斜率
P
Q
o
x
y
y=f(x)
割线
切线
T
请看当点Q
沿着曲线
逐渐向点P
接近时,
割线PQ绕着
点P逐渐转动
的情况.
割线PQ越来越接近曲线在点P的切线
过点P的切线PT最贴近点P附近的曲线f(x) ,因此,在P
附近,曲线f(x)就可以用过点P的切线PT来代替
以直代曲
阅读课本9页的文字说明,体会在微积分中“以直代曲”的思想,
体验数学中以简单的对象代替复杂的解题思路
T5
某时刻血管中药物的浓度的瞬间变化率,
即等于函数图像上该点处的切线的斜率
什么是导函数
由函数f(x)在x=x0处求导数的过程可以看到,
f ’(x0) 是一个确定的数.那么,当x0变化时, f ’(x0) 有且只有一个值与之对应;所以, f ’(x) 是x的一个函数,我们叫它为f(x)的导函数.
t
0.2
0.4
0.6
0.8
0.4
0
-0.7
-1.4
这是用列表法来表示函数的对应关系!
导函数,实际是函数的自变量与其该点处的切线的斜率
的一种对应关系
在不致发生混淆时,导函数也简称导数.
T6,BT1
(3)函数f(x)在点x0处的导数 就是导函数
在x=x0处的函数值,即 。这也是
求函数在点x0处的导数的方法之一。
(2)函数的导数,是指某一区间内任意点x而言的,
就是函数f(x)的导函数 。
(1)函数在一点处的导数,就是在该点的函数的改
变量与自变量的改变量之比的极限,它是一个
常数,不是变数。
弄清“函数f(x)在点x0处的导数”、“导函数”、“导数”
之间的区别与联系。
小结:
一、函数在某处的导数的几何意义:
函数图像上该点处的切线的斜率
用途1:求解曲线上某点的切线方程
用途2:利用导数的几何性质“以直代曲”的数学思想
二、导函数的概念及相关概念的区别
导数的几何意义1
先来复习导数的概念
1.函数的平均变化率
2、 t0时刻的瞬时速度
如果函数y=f(x)在点x=x0存在导数,就说函数y=f(x)在点x0处可导,如果极限不存在,就说函数 f(x)在点x0处不可导.
由导数的意义可知,求函数y=f(x)在点x0处的导数的基本方法是:
注意:
这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.
β
y=f(x)
P
Q
M
Δx
Δy
O
x
y
β
P
y=f(x)
Q
M
Δx
Δy
O
x
y
如图,曲线C是函数y=f(x)
的图象,P(x0,y0)是曲线C上的
任意一点,Q(x0+Δx,y0+Δy)
为P邻近一点,PQ为C的割线,
PM//x轴,QM//y轴,β为PQ的
倾斜角.
下面来看导数的几何意义:
割线的斜率
P
Q
o
x
y
y=f(x)
割线
切线
T
请看当点Q沿着曲线逐渐向点P接近时,
割线PQ绕着
点P逐渐转动
的情况.
割线PQ越来越接近曲线在点P的切线
我们发现,当点Q沿着曲线无限接近点P即Δx→0时,割线PQ有一个极限位置PT.则我们把直线PT称为曲线在点P处的切线.
设切线的倾斜角为α,那么当Δx→0时,割线PQ的斜率,称为曲线在点P处的切线的斜率.
即:
这个概念:①提供了求曲线上某点切线的斜率的一种方法;②切线斜率的本质——函数在x=x0处的导数.
例1:求曲线y=f(x)=x2+1在点P(1,2)
处的切线方程.
P
y
=
x
2
+1
x
y
-
1
1
1
O
因此,切线方程为y-2=2(x-1),
即y=2x.
求曲线在某点处的切线方程
的基本步骤:
先利用切线斜率的定义求出切线的斜率,
然后利用点斜式求切线方程.
曲线某点的切线的斜率
等于函数在该点处的导数
练习:如图已知曲线 ,求:
(1)点P处的切线的斜率; (2)点P处的切线方程.
y
x
-2
-1
1
2
-2
-1
1
2
3
4
O
P
即点P处的切线的斜率等于4.
(2)在点P处的切线方程是y-8/3=4(x-2),
即12x-3y-16=0.
(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。
(2)根据直线方程的点斜式写出切线方程,即
d.求切线方程的步骤:
例:求过点P(3,5)且与曲线y=x2相切的直线方程.
说明:曲线上求在点P处的切线与求过点P的切线有区别.
在点P处的切线,点P必为切点,求过点P的切线,点P
未必是切点.应注意概念的区别,其求法也有所不同.
解:设所求切线的切点在A(x0,y0).
因为A是曲线y=x2上的一点,所以,y0=x02 ①.
又因为函数y=x2的导数为 所以过点A(x0,y0)的
切线的斜率为
由于所求切线过P(3,5)和A(x0,y0)两点,故其斜率又
应为 ②.
联立①,②解得:
故切点分别为(1,1)或(5,25).
当切点为(1,1)时,切线的斜率为k1=2x0=2;
当切点为(5,25)时,切线的斜率为k2=2x0=10;
所以所求的切线有两条,方程分别为:y-1=2(x-1)或y-25=10(x-5),即y=2x-1或y=10x-25.
某时刻血管中药物的浓度的瞬间变化率,
即等于函数图像上该点处的切线的斜率
小结:
函数在某处的导数的几何意义:
函数图像上该点处的切线的斜率
1、用途1:求解曲线上某点的切线方程
2:求过点P(8,-3)且与曲线y=1/x相切的直线方程.
1、已知曲线 f(x)=3x2+x-1上的一点P,横坐标为-2,
求:(1)点P处的切线的斜率; (2)点P处的切线方程.
作业
P11;T4
导数的几何意义2
函数在某处的导数的几何意义:
朝花夕拾
函数在某处的导数值等于函数图像上
该点处的切线的斜率
P
Q
o
x
y
y=f(x)
割线
切线
T
请看当点Q
沿着曲线
逐渐向点P
接近时,
割线PQ绕着
点P逐渐转动
的情况.
割线PQ越来越接近曲线在点P的切线
过点P的切线PT最贴近点P附近的曲线f(x) ,因此,在P
附近,曲线f(x)就可以用过点P的切线PT来代替
以直代曲
阅读课本9页的文字说明,体会在微积分中“以直代曲”的思想,
体验数学中以简单的对象代替复杂的解题思路
T5
某时刻血管中药物的浓度的瞬间变化率,
即等于函数图像上该点处的切线的斜率
什么是导函数
由函数f(x)在x=x0处求导数的过程可以看到,
f ’(x0) 是一个确定的数.那么,当x0变化时, f ’(x0) 有且只有一个值与之对应;所以, f ’(x) 是x的一个函数,我们叫它为f(x)的导函数.
t
0.2
0.4
0.6
0.8
0.4
0
-0.7
-1.4
这是用列表法来表示函数的对应关系!
导函数,实际是函数的自变量与其该点处的切线的斜率
的一种对应关系
在不致发生混淆时,导函数也简称导数.
T6,BT1
(3)函数f(x)在点x0处的导数 就是导函数
在x=x0处的函数值,即 。这也是
求函数在点x0处的导数的方法之一。
(2)函数的导数,是指某一区间内任意点x而言的,
就是函数f(x)的导函数 。
(1)函数在一点处的导数,就是在该点的函数的改
变量与自变量的改变量之比的极限,它是一个
常数,不是变数。
弄清“函数f(x)在点x0处的导数”、“导函数”、“导数”
之间的区别与联系。
小结:
一、函数在某处的导数的几何意义:
函数图像上该点处的切线的斜率
用途1:求解曲线上某点的切线方程
用途2:利用导数的几何性质“以直代曲”的数学思想
二、导函数的概念及相关概念的区别
