人教版数学六年级上册 第五单元综合能力评价课件(共22张PPT)
文档属性
| 名称 | 人教版数学六年级上册 第五单元综合能力评价课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 246.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
综合能力评价
第五单元综合能力评价
一、填一填。(24%)
1.在一个边长是10 cm的正方形里画一个最大的圆,圆规两脚之间的距离是( )cm。
2.把一个半径是3 cm的圆连续对折两次,得到一个圆心角是( )°的扇形,这个扇形的面积是( )cm2。
5
90
7.065
3.圆有( )条对称轴;半圆有( )条对称轴;圆环有( )条对称轴。
4.大圆的半径是6 cm,小圆的直径是6 cm,大圆和小圆的半径比是( ),直径比是( ),周长比是( ),面积比是( )。
无数
1
无数
2∶1
2∶1
2∶1
4∶1
5.一个半圆环,外圆半径是6 cm,内圆半径是4 cm,环宽是( )cm,这个半圆环的面积是( )cm2。
6.要用圆规画一个面积是28.26 cm2的圆,圆规两脚之间的距离是( )cm,这个圆的周长是( )cm。
7.在周长是20 cm的正方形里画一个最大的扇形,这个扇形的面积是( )cm2。
2
31.4
3
18.84
19.625
8.一个半圆形铁片的半径是10 cm,它的周长是( ),它的面积是( )。
9.在一个边长是20 cm的正方形里剪下四个同样大小的圆,这四个圆的半径最大是( )cm,周长最大是( )cm,面积最大是( )cm2。
51.4 cm
157 cm2
5
31.4
78.5
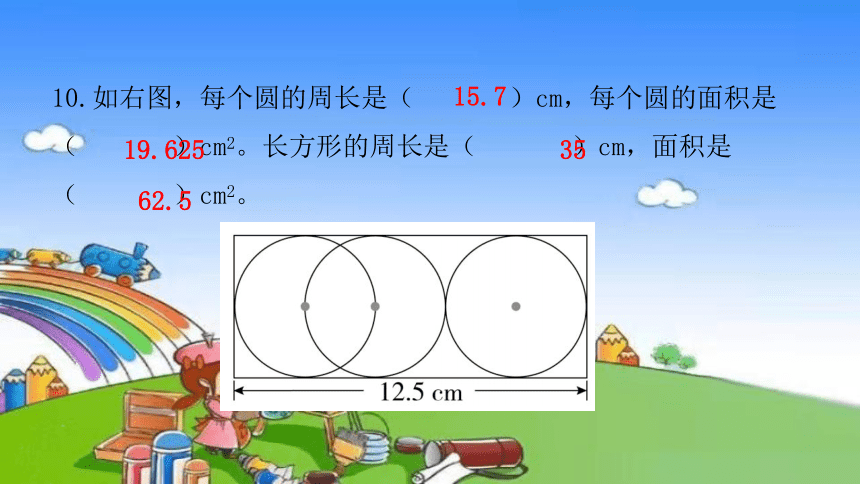
10.如右图,每个圆的周长是( )cm,每个圆的面积是( )cm2。长方形的周长是( )cm,面积是( )cm2。
15.7
19.625
35
62.5
二、辨一辨。(对的在括号内画“√”,错的画“×”)(5%)
1.两个半圆一定能拼成一个完整的圆。 ( )
2.一个圆的直径越大,面积也越大,圆周率也越大。( )
3.半径是一条射线。( )
4.一个圆的周长与其半径的比值是2π。( )
5.在同一个圆里,两条半径就是一条直径。( )
×
×
×
√
×
三、选一选。(将正确答案的字母编号填在括号里)(7%)
1.在长4 cm、宽3 cm的长方形内画一个最大的半圆,这个半圆的周长是( )。
A.6.28 cm B.7.71 cm C.10.28 cm
2.一枚圆形硬币滚动两周的长是12.56 cm,那么这个硬币的直径是( )cm。
A.12.56 B.4 C.2
C
C
3.一个圆的半径从3 cm增加到5 cm,周长增加( )cm,面积增加( )cm2。
A.12.56 B.25.12 C.50.24
4.第一个扇形的圆心角是180°,第二个扇形的圆心角是90°,那么两个扇形面积相比较,( )。
A.第一个扇形的面积大 B.第二个扇形的面积大
C.无法比较
C
A
C
5.一个圆环,大圆的直径是6 cm,小圆的半径是2 cm,则圆环的宽是( )cm。
A.5 B.6 C.1
6.一个挂钟的分针长10 cm,经过60分钟后,分针的尖端走的路程是多少厘米?这道题实际上是求圆的( )。
A.半径 B.周长 C.面积
7.半径是2 cm的圆,它的周长和面积( )。
A.周长比较大 B.面积比较大 C.无法比较
C
B
C
四、填表。(12%)
圆的半径/cm 圆的直径/cm 圆的周长/cm 圆的面积/cm2
3 __________ __________ __________
__________ 8 __________ __________
__________ __________ 314 __________
__________ 14 __________ __________
6
18.84
28.26
4
25.12
50.24
50
100
7850
7
43.96
153.86
五、操作。(20%)
1.用圆规画一个半径是1.5 cm的圆,再在圆中画一个圆心角是150°的扇形。(4%)
略
2.画出下图所有的对称轴。(4%)
略
3.求出下列图形阴影部分的周长。(图中单位:cm)(6%)
(1) (2)
3.14×4+4×2=20.56(cm)
3.14×10+10×4=71.4(cm)
4.求出下面图形阴影部分的面积。(图中单位:cm)(6%)
(1) (2)
16×8-3.14×82÷4=
77.76(cm2)
六、解决问题。(32%)
1.一个钟表的时针长5 cm,经过24小时,时针扫过的面积是多少?(4%)
3.14×52×2=157(cm2)
答:时针扫过的面积是157 cm2。
2.用一根长35 dm的绳子绕一棵树干,绕了5圈还剩下3.6 dm,这个树干的半径是多少?(5%)
(35-3.6)÷5÷3.14÷2=1(dm)
答:这个树干的半径是1 dm。
3.有一个周长是62.8 m的圆形草坪,现准备在草坪中心装一个自动旋转喷灌装置,有射程为20 m,15 m,10 m的三种装置,应该选择哪一种装置?为什么?(5%)
62.8÷3.14÷2=10(m)
答:应选射程为10 m的装置。
4.一个可近似看作圆形的湖,直径是500 m。(12%)
(1)沿着湖边每隔5 m种一棵树,一共要种多少棵树?
3.14×500÷5=314(棵)
答:一共要种314棵树。
(2)如果每平方米的水域要投放0.5 kg鱼苗,一共要投放多少千克鱼苗?
3.14×(500÷2)2×0.5=98125(kg)
答:一共要投放98125 kg鱼苗。
(3)在这个湖边有一条宽3 m的绿道供市民散步,这条绿道的面积是多少?
3.14×[(500÷2+3)2-(500÷2)2]=4738.26(m2)
答:这条绿道的面积是4738.26 m2。
5.一个正方形和一个圆的周长相等,如果圆的半径是15 cm,那么正方形的边长是多少?(6%)
2×3.14×15=94.2(cm)
94.2÷4=23.55(cm)
答:正方形的边长是23.55 cm。
综合能力评价
第五单元综合能力评价
一、填一填。(24%)
1.在一个边长是10 cm的正方形里画一个最大的圆,圆规两脚之间的距离是( )cm。
2.把一个半径是3 cm的圆连续对折两次,得到一个圆心角是( )°的扇形,这个扇形的面积是( )cm2。
5
90
7.065
3.圆有( )条对称轴;半圆有( )条对称轴;圆环有( )条对称轴。
4.大圆的半径是6 cm,小圆的直径是6 cm,大圆和小圆的半径比是( ),直径比是( ),周长比是( ),面积比是( )。
无数
1
无数
2∶1
2∶1
2∶1
4∶1
5.一个半圆环,外圆半径是6 cm,内圆半径是4 cm,环宽是( )cm,这个半圆环的面积是( )cm2。
6.要用圆规画一个面积是28.26 cm2的圆,圆规两脚之间的距离是( )cm,这个圆的周长是( )cm。
7.在周长是20 cm的正方形里画一个最大的扇形,这个扇形的面积是( )cm2。
2
31.4
3
18.84
19.625
8.一个半圆形铁片的半径是10 cm,它的周长是( ),它的面积是( )。
9.在一个边长是20 cm的正方形里剪下四个同样大小的圆,这四个圆的半径最大是( )cm,周长最大是( )cm,面积最大是( )cm2。
51.4 cm
157 cm2
5
31.4
78.5
10.如右图,每个圆的周长是( )cm,每个圆的面积是( )cm2。长方形的周长是( )cm,面积是( )cm2。
15.7
19.625
35
62.5
二、辨一辨。(对的在括号内画“√”,错的画“×”)(5%)
1.两个半圆一定能拼成一个完整的圆。 ( )
2.一个圆的直径越大,面积也越大,圆周率也越大。( )
3.半径是一条射线。( )
4.一个圆的周长与其半径的比值是2π。( )
5.在同一个圆里,两条半径就是一条直径。( )
×
×
×
√
×
三、选一选。(将正确答案的字母编号填在括号里)(7%)
1.在长4 cm、宽3 cm的长方形内画一个最大的半圆,这个半圆的周长是( )。
A.6.28 cm B.7.71 cm C.10.28 cm
2.一枚圆形硬币滚动两周的长是12.56 cm,那么这个硬币的直径是( )cm。
A.12.56 B.4 C.2
C
C
3.一个圆的半径从3 cm增加到5 cm,周长增加( )cm,面积增加( )cm2。
A.12.56 B.25.12 C.50.24
4.第一个扇形的圆心角是180°,第二个扇形的圆心角是90°,那么两个扇形面积相比较,( )。
A.第一个扇形的面积大 B.第二个扇形的面积大
C.无法比较
C
A
C
5.一个圆环,大圆的直径是6 cm,小圆的半径是2 cm,则圆环的宽是( )cm。
A.5 B.6 C.1
6.一个挂钟的分针长10 cm,经过60分钟后,分针的尖端走的路程是多少厘米?这道题实际上是求圆的( )。
A.半径 B.周长 C.面积
7.半径是2 cm的圆,它的周长和面积( )。
A.周长比较大 B.面积比较大 C.无法比较
C
B
C
四、填表。(12%)
圆的半径/cm 圆的直径/cm 圆的周长/cm 圆的面积/cm2
3 __________ __________ __________
__________ 8 __________ __________
__________ __________ 314 __________
__________ 14 __________ __________
6
18.84
28.26
4
25.12
50.24
50
100
7850
7
43.96
153.86
五、操作。(20%)
1.用圆规画一个半径是1.5 cm的圆,再在圆中画一个圆心角是150°的扇形。(4%)
略
2.画出下图所有的对称轴。(4%)
略
3.求出下列图形阴影部分的周长。(图中单位:cm)(6%)
(1) (2)
3.14×4+4×2=20.56(cm)
3.14×10+10×4=71.4(cm)
4.求出下面图形阴影部分的面积。(图中单位:cm)(6%)
(1) (2)
16×8-3.14×82÷4=
77.76(cm2)
六、解决问题。(32%)
1.一个钟表的时针长5 cm,经过24小时,时针扫过的面积是多少?(4%)
3.14×52×2=157(cm2)
答:时针扫过的面积是157 cm2。
2.用一根长35 dm的绳子绕一棵树干,绕了5圈还剩下3.6 dm,这个树干的半径是多少?(5%)
(35-3.6)÷5÷3.14÷2=1(dm)
答:这个树干的半径是1 dm。
3.有一个周长是62.8 m的圆形草坪,现准备在草坪中心装一个自动旋转喷灌装置,有射程为20 m,15 m,10 m的三种装置,应该选择哪一种装置?为什么?(5%)
62.8÷3.14÷2=10(m)
答:应选射程为10 m的装置。
4.一个可近似看作圆形的湖,直径是500 m。(12%)
(1)沿着湖边每隔5 m种一棵树,一共要种多少棵树?
3.14×500÷5=314(棵)
答:一共要种314棵树。
(2)如果每平方米的水域要投放0.5 kg鱼苗,一共要投放多少千克鱼苗?
3.14×(500÷2)2×0.5=98125(kg)
答:一共要投放98125 kg鱼苗。
(3)在这个湖边有一条宽3 m的绿道供市民散步,这条绿道的面积是多少?
3.14×[(500÷2+3)2-(500÷2)2]=4738.26(m2)
答:这条绿道的面积是4738.26 m2。
5.一个正方形和一个圆的周长相等,如果圆的半径是15 cm,那么正方形的边长是多少?(6%)
2×3.14×15=94.2(cm)
94.2÷4=23.55(cm)
答:正方形的边长是23.55 cm。
