有理数的乘方[上学期]
图片预览






文档简介
课件20张PPT。读一读 棋盘上的学问 古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗? 事实上,按照这个大臣的要求,放满一个棋盘上的64个
格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616有理数的乘方(1)
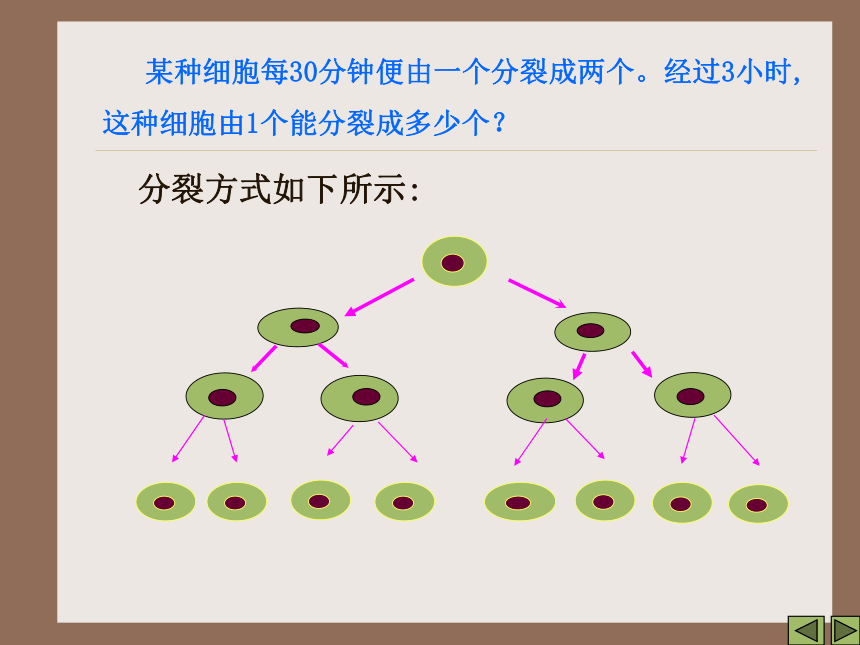
设计者:王教学目标了解乘方的意义并能正确的读、写;掌握幂的性质并能进行乘方的运算。能力目标通过乘方运算,培养运算能力;培养观察、类比、归纳、知识迁移的能力。知识目标 某种细胞每30分钟便由一个分裂成两个。经过3小时,
这种细胞由1个能分裂成多少个?分裂方式如下所示:那么,3小时共分裂了多少次?答: 一次得 : 两次 :
三次 :
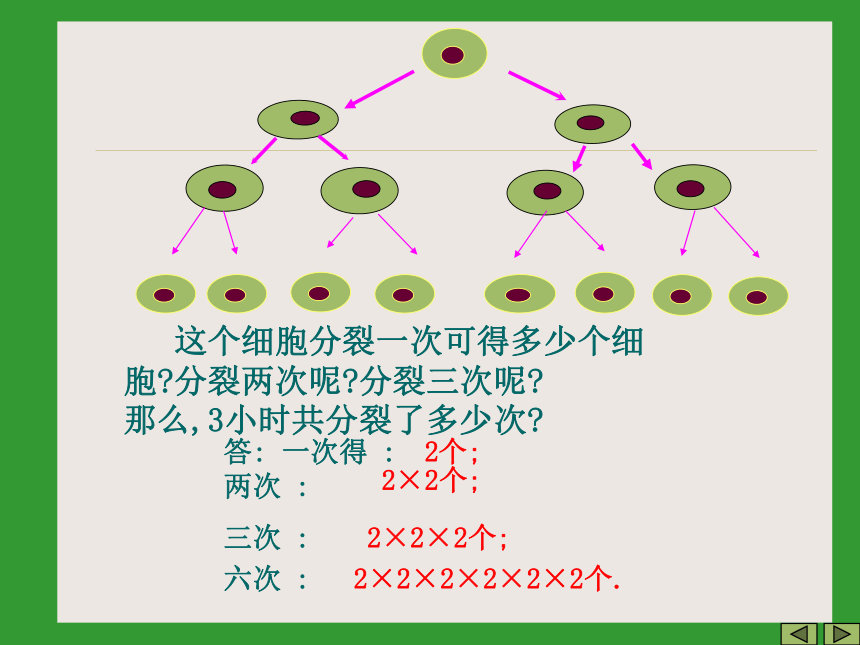
2个;2×2个;2×2×2个; 六次 : 2×2×2×2×2×2个. 这个细胞分裂一次可得多少个细胞?分裂两次呢?分裂三次呢?请认真观察下面的式子:
2×2.
2×2×2×2.
2×2×2×2×2×2.
2×2×2×2 × 2×2×2×2.它们有什么相同点?答:它们都是乘法;并且它们各自的因数都相同.这样的运算我们叫作乘方运算.
2 ×2×2×2×2×2记作: ____ 用简便记法表示下列各算式:
2×2×2=______.
(2) 3×3×3×3=_______.
6×6×6×6×6=______.
(4) a×a×a×a×a=_______.26233465a5 其中a代表相同的因数,n代表相乘
因数的个数. 一般的,任意多个相同的有理数相乘,我们常记作:乘方: 求n个相同因数a的积的运算.
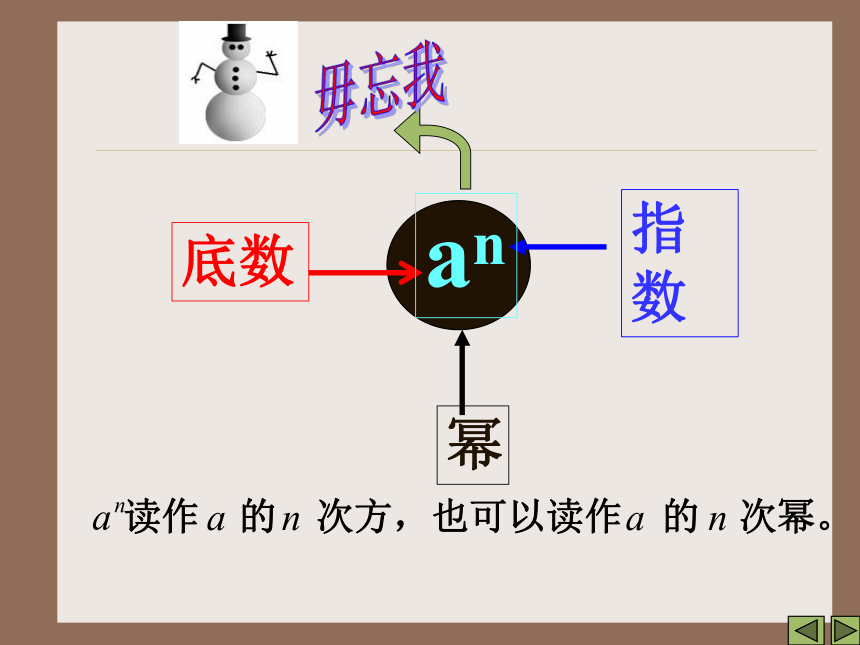
an 读作 的 次方,也可以读作 的 次幂。
毋忘我 (1)在64中,底数是___,指数____;(3)在(-6)5中,底数是 ___, 指______;写出下列各幂的底数与指数:-64a465(2)在a4中,底数是___,指数是____;(4)在-25中,底数是____,指数是____;25祝你成功例1 计算:解(1)53 = 5×5×5=125; (2) =(-3) ×(-3) ×(-3) ×(-3)=81.(1) 53, (2) (-3)4; (3) (-1/2)3.(3)=(-1/2) × (-1/2) × (-1/2)= -1/8.注意:当底数是负数或分数时,
底数一定要加上括弧,
这也是辩认底数的方法.例2 计算:(1)102 , 103 , 104;解:(1)102 =10×10=103 = =1000;100;10 ×10×10(2)(-10)2=100(-10)3 =(-10)4 ==-1000;=(-10)×(-10)(-10)×(-10) ×(-10)(-10) ×(-10)×(-10)× (-10)=10000。104 =10 ×10×10 ×10=10000观察例2的结果,你能发现什么规律?答:10的几次方,1后面就有几个0;想一想:你还能发现什么规律?答:正数的任何次幂还是正数;而负数的奇次幂是负数;偶次幂是正数。随堂练习:在74中,底数是____,指数是____;在(-1.5)5中,底数是 ___, 指数____. 2. 计算: (1) (-2)4; (2) -24; (3) (-1.5)2 4.一个数的平方为16,这个数可能是几?一个数的平方可能是零吗?75-1.543.你能说出(-2)4、 -24区别与联系吗?2. 解:
(1) (-2)4= (-2) × (-2) ×(-2) ×(-2) =16;
(2) -24= -2 × 2 × 2 × 2 = -16;
(3) (-1.5)2= (-1.5) × (-1.5)=2.25.随堂练习:在74中,底数是____,指数是____;在(-1.5)5中,底数是 ___, 指数____. 2. 计算: (1) (-2)4; (2) -24; (3) (-1.5)2 4.一个数的平方为16,这个数可能是几?一个数的平方可能是零吗?75-1.543.你能说出(-2)4、 -24区别与联系吗?试一试 你一定会成功小结:一分耕耘,一分收获你能告诉我这节课的收获吗?考考你相信你是最棒的!1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
考考你相信你是最棒的!1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;46-4的7次方或-4的7次幂负-8
作业:
P74 2(2)(4)(6),
3。
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗? 事实上,按照这个大臣的要求,放满一个棋盘上的64个
格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616有理数的乘方(1)
设计者:王教学目标了解乘方的意义并能正确的读、写;掌握幂的性质并能进行乘方的运算。能力目标通过乘方运算,培养运算能力;培养观察、类比、归纳、知识迁移的能力。知识目标 某种细胞每30分钟便由一个分裂成两个。经过3小时,
这种细胞由1个能分裂成多少个?分裂方式如下所示:那么,3小时共分裂了多少次?答: 一次得 : 两次 :
三次 :
2个;2×2个;2×2×2个; 六次 : 2×2×2×2×2×2个. 这个细胞分裂一次可得多少个细胞?分裂两次呢?分裂三次呢?请认真观察下面的式子:
2×2.
2×2×2×2.
2×2×2×2×2×2.
2×2×2×2 × 2×2×2×2.它们有什么相同点?答:它们都是乘法;并且它们各自的因数都相同.这样的运算我们叫作乘方运算.
2 ×2×2×2×2×2记作: ____ 用简便记法表示下列各算式:
2×2×2=______.
(2) 3×3×3×3=_______.
6×6×6×6×6=______.
(4) a×a×a×a×a=_______.26233465a5 其中a代表相同的因数,n代表相乘
因数的个数. 一般的,任意多个相同的有理数相乘,我们常记作:乘方: 求n个相同因数a的积的运算.
an 读作 的 次方,也可以读作 的 次幂。
毋忘我 (1)在64中,底数是___,指数____;(3)在(-6)5中,底数是 ___, 指______;写出下列各幂的底数与指数:-64a465(2)在a4中,底数是___,指数是____;(4)在-25中,底数是____,指数是____;25祝你成功例1 计算:解(1)53 = 5×5×5=125; (2) =(-3) ×(-3) ×(-3) ×(-3)=81.(1) 53, (2) (-3)4; (3) (-1/2)3.(3)=(-1/2) × (-1/2) × (-1/2)= -1/8.注意:当底数是负数或分数时,
底数一定要加上括弧,
这也是辩认底数的方法.例2 计算:(1)102 , 103 , 104;解:(1)102 =10×10=103 = =1000;100;10 ×10×10(2)(-10)2=100(-10)3 =(-10)4 ==-1000;=(-10)×(-10)(-10)×(-10) ×(-10)(-10) ×(-10)×(-10)× (-10)=10000。104 =10 ×10×10 ×10=10000观察例2的结果,你能发现什么规律?答:10的几次方,1后面就有几个0;想一想:你还能发现什么规律?答:正数的任何次幂还是正数;而负数的奇次幂是负数;偶次幂是正数。随堂练习:在74中,底数是____,指数是____;在(-1.5)5中,底数是 ___, 指数____. 2. 计算: (1) (-2)4; (2) -24; (3) (-1.5)2 4.一个数的平方为16,这个数可能是几?一个数的平方可能是零吗?75-1.543.你能说出(-2)4、 -24区别与联系吗?2. 解:
(1) (-2)4= (-2) × (-2) ×(-2) ×(-2) =16;
(2) -24= -2 × 2 × 2 × 2 = -16;
(3) (-1.5)2= (-1.5) × (-1.5)=2.25.随堂练习:在74中,底数是____,指数是____;在(-1.5)5中,底数是 ___, 指数____. 2. 计算: (1) (-2)4; (2) -24; (3) (-1.5)2 4.一个数的平方为16,这个数可能是几?一个数的平方可能是零吗?75-1.543.你能说出(-2)4、 -24区别与联系吗?试一试 你一定会成功小结:一分耕耘,一分收获你能告诉我这节课的收获吗?考考你相信你是最棒的!1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
考考你相信你是最棒的!1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;46-4的7次方或-4的7次幂负-8
作业:
P74 2(2)(4)(6),
3。
