教科版(2019)> 必修 第一册2.4 匀变速直线运动规律的应匀变速直线运动规律的应用(共18张)
文档属性
| 名称 | 教科版(2019)> 必修 第一册2.4 匀变速直线运动规律的应匀变速直线运动规律的应用(共18张) |  | |
| 格式 | zip | ||
| 文件大小 | 324.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-15 12:26:37 | ||
图片预览




文档简介
(共18张PPT)
§1.8 匀变速直线运动规律的应用
自学思考:
1、从飞机跑道设计的“活动”中你有哪些启示?
2、描述物体运动的物理量有哪些;它们之间有何关系?
3、已学的公式有哪些;如何选择呢?
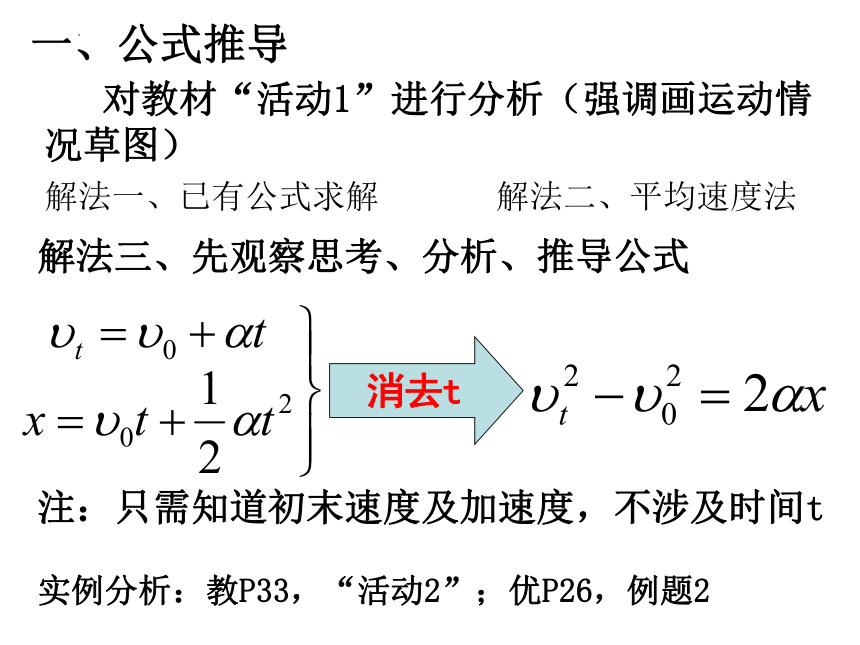
一、公式推导
对教材“活动1”进行分析(强调画运动情况草图)
解法一、已有公式求解 解法二、平均速度法
解法三、先观察思考、分析、推导公式
消去t
注:只需知道初末速度及加速度,不涉及时间t
实例分析:教P33,“活动2”;优P26,例题2
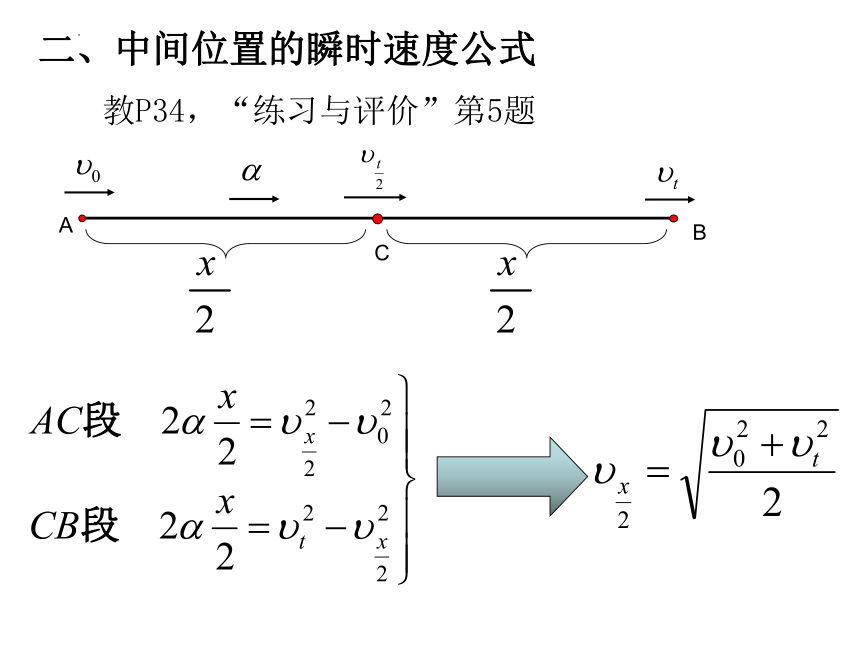
二、中间位置的瞬时速度公式
教P34,“练习与评价”第5题
B
A
C
拓展思考?
方法一:做差法
方法二:做比法
方法三:v-t图像法
方法四:分析法
结论:
无论是在匀加速直线运动中还是在匀减速直线运动中,都是中间位置的瞬时速度大于中间时刻的瞬时速度。
三、已学运动学公式
思考:如何选择这些公式?
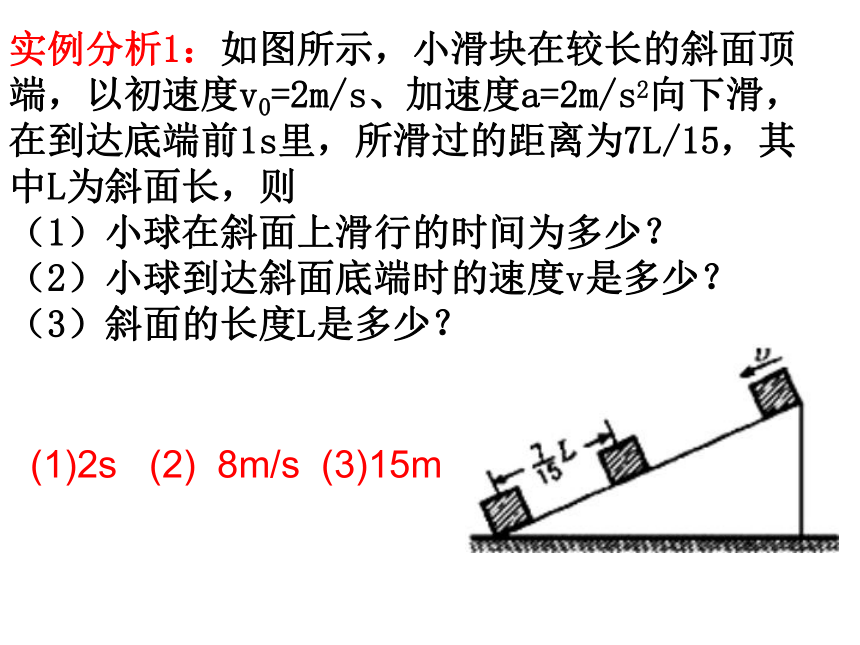
实例分析1:如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s里,所滑过的距离为7L/15,其中L为斜面长,则
(1)小球在斜面上滑行的时间为多少?
(2)小球到达斜面底端时的速度v是多少?
(3)斜面的长度L是多少?
(1)2s (2) 8m/s (3)15m
实例分析2、一物体以某一初速度在粗糙的平面上做匀减速直线运动,最后静止下来.若此物体在最初5s内通过的位移与最后5s内通过的位移之比为11:5,求此物体一共运动多长时间.
8s
变式思考:
某一初速度冲上斜面顶端,最后2s时间内的位移为1m;求:初速度及加速度?
小结:描述物体运动的五个物理学参量的关系
知三求二
四、追击相遇问题
典型题型分析
例1:一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始加速行驶,恰在这时一辆自行车以6m/s的速度匀速驶来,从后边超过汽车。试求:
1、汽车何时追上乙车,此时距离路口多远?
2、汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
方法一:公式法
方法二:图像法
例2:A火车以v1=20m/s速度匀速行驶,司机发现前方同轨道上相距100m处有另一列火车B正以v2=10m/s速度匀速行驶,A车立即做加速度大小为a的匀减速直线运动。要使两车不相撞,a应满足什么条件?
【跟踪练习1】
平直的公路上有甲、乙两辆汽车,甲车以0.5m/s2的加速度由静止开始加速行驶;乙车在甲车前方200m处以5m/s的速度做同向的匀速运动。求:
1、甲车追上乙车时的速度是多大,此时甲车运动了多远?
2、甲车在追赶乙车的过程中两车何时相距最远?
ν甲=20m/s x甲=400m
Xm=225m
甲车以加速度3m/s2由静止开始做匀加速直线运动.乙车落后2s在同一地点由静止开始,以加速度6m/s2做匀加速直线运动.两车的运动方向相同.求:
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)乙车出发后经多长时间可追上甲车?
【跟踪练习2】
随堂练习:
优P27,例4;P28,8题
小结:解题思路
1、两个关系:时间关系:
位移关系:
2、一个条件:两者速度相等
两者速度相等,往往是物体间能否追上,或两者距离最大、最小的临界条件,是分析判断的切入点。
3、解题方法
(1)画清行程草图,找出两物体间的时间、位移关系
(2)仔细审题,挖掘临界条件,建立方程
(3)利用公式法、图像法、二次函数求极值、相对运动知识求解
紧抓一图三式
五、多过程问题
例题1、物块静止开始沿长度为4m的斜面滑下,到达水平地面后(经过斜面底端时只改变速度方向大小不变)又在水平地面上滑行了6m停下,整个过程用时10s。分别求物体在斜面和水平面上的加速度大小。
例题2、一跳伞运动员做低空跳伞表演,飞机在离地面224m高空水平飞行,设运动员离开飞机后在竖直方向上先做自由落体运动;经过一段时间后,立即打开降落伞,展开伞后运动员以12.5m/s2的加速度在竖直方向上匀减速下降,为了运动员的安全,要求运动员落地时竖直方向的速度为5m/s,g=10m/s2求:
(1)运动员刚展开降落伞时的速度为多大?此时他离地的高度多大?
(2)运动员在空中下落的总时间为多少?
8.6s
99m
小结:关于多过程的问题关键点是抓住
中间转折点的速度
跟踪练习:优P29,6题
例题1、如图所示,表示一质点在6 s内的x-t图象,试据此分析质点的运动情况并画出它的v-t图象.
斜率表示速度
解析
0~2s的速度
2~4s的速度
4~6s的速度
六、图像问题
针对训练1 若将上图中的纵坐标由“x”改为“v”,即如图象所示.
(1)试分析各段的运动情况
(2)画出它的a-t图.
斜率表示加速度
解析
0~2s加速度
2~4s加速度
4~6s加速度
针对训练2 在如图所示的位移(x)—时间(t)图象和速度(v)—时间(t)图象中,给出的四条图线甲、乙、丙、丁分别代表四辆车由同一地点向同一方向运动的情况,则下列说法正确的是( )
A.t1时刻,乙车追上甲车
B.0~t1时间内,甲、乙两车的平均速度相等
C.丙、丁两车在t2时刻相遇
D.0~t2时间内,丙、丁两车的平均速度相等
相遇
△x相同
速度相等
面积表位移
x丙> x丁
AB
课后练习
教P34,“练习与评价”,2题
§1.8 匀变速直线运动规律的应用
自学思考:
1、从飞机跑道设计的“活动”中你有哪些启示?
2、描述物体运动的物理量有哪些;它们之间有何关系?
3、已学的公式有哪些;如何选择呢?
一、公式推导
对教材“活动1”进行分析(强调画运动情况草图)
解法一、已有公式求解 解法二、平均速度法
解法三、先观察思考、分析、推导公式
消去t
注:只需知道初末速度及加速度,不涉及时间t
实例分析:教P33,“活动2”;优P26,例题2
二、中间位置的瞬时速度公式
教P34,“练习与评价”第5题
B
A
C
拓展思考?
方法一:做差法
方法二:做比法
方法三:v-t图像法
方法四:分析法
结论:
无论是在匀加速直线运动中还是在匀减速直线运动中,都是中间位置的瞬时速度大于中间时刻的瞬时速度。
三、已学运动学公式
思考:如何选择这些公式?
实例分析1:如图所示,小滑块在较长的斜面顶端,以初速度v0=2m/s、加速度a=2m/s2向下滑,在到达底端前1s里,所滑过的距离为7L/15,其中L为斜面长,则
(1)小球在斜面上滑行的时间为多少?
(2)小球到达斜面底端时的速度v是多少?
(3)斜面的长度L是多少?
(1)2s (2) 8m/s (3)15m
实例分析2、一物体以某一初速度在粗糙的平面上做匀减速直线运动,最后静止下来.若此物体在最初5s内通过的位移与最后5s内通过的位移之比为11:5,求此物体一共运动多长时间.
8s
变式思考:
某一初速度冲上斜面顶端,最后2s时间内的位移为1m;求:初速度及加速度?
小结:描述物体运动的五个物理学参量的关系
知三求二
四、追击相遇问题
典型题型分析
例1:一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始加速行驶,恰在这时一辆自行车以6m/s的速度匀速驶来,从后边超过汽车。试求:
1、汽车何时追上乙车,此时距离路口多远?
2、汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
方法一:公式法
方法二:图像法
例2:A火车以v1=20m/s速度匀速行驶,司机发现前方同轨道上相距100m处有另一列火车B正以v2=10m/s速度匀速行驶,A车立即做加速度大小为a的匀减速直线运动。要使两车不相撞,a应满足什么条件?
【跟踪练习1】
平直的公路上有甲、乙两辆汽车,甲车以0.5m/s2的加速度由静止开始加速行驶;乙车在甲车前方200m处以5m/s的速度做同向的匀速运动。求:
1、甲车追上乙车时的速度是多大,此时甲车运动了多远?
2、甲车在追赶乙车的过程中两车何时相距最远?
ν甲=20m/s x甲=400m
Xm=225m
甲车以加速度3m/s2由静止开始做匀加速直线运动.乙车落后2s在同一地点由静止开始,以加速度6m/s2做匀加速直线运动.两车的运动方向相同.求:
(1)在乙车追上甲车之前,两车距离的最大值是多少?
(2)乙车出发后经多长时间可追上甲车?
【跟踪练习2】
随堂练习:
优P27,例4;P28,8题
小结:解题思路
1、两个关系:时间关系:
位移关系:
2、一个条件:两者速度相等
两者速度相等,往往是物体间能否追上,或两者距离最大、最小的临界条件,是分析判断的切入点。
3、解题方法
(1)画清行程草图,找出两物体间的时间、位移关系
(2)仔细审题,挖掘临界条件,建立方程
(3)利用公式法、图像法、二次函数求极值、相对运动知识求解
紧抓一图三式
五、多过程问题
例题1、物块静止开始沿长度为4m的斜面滑下,到达水平地面后(经过斜面底端时只改变速度方向大小不变)又在水平地面上滑行了6m停下,整个过程用时10s。分别求物体在斜面和水平面上的加速度大小。
例题2、一跳伞运动员做低空跳伞表演,飞机在离地面224m高空水平飞行,设运动员离开飞机后在竖直方向上先做自由落体运动;经过一段时间后,立即打开降落伞,展开伞后运动员以12.5m/s2的加速度在竖直方向上匀减速下降,为了运动员的安全,要求运动员落地时竖直方向的速度为5m/s,g=10m/s2求:
(1)运动员刚展开降落伞时的速度为多大?此时他离地的高度多大?
(2)运动员在空中下落的总时间为多少?
8.6s
99m
小结:关于多过程的问题关键点是抓住
中间转折点的速度
跟踪练习:优P29,6题
例题1、如图所示,表示一质点在6 s内的x-t图象,试据此分析质点的运动情况并画出它的v-t图象.
斜率表示速度
解析
0~2s的速度
2~4s的速度
4~6s的速度
六、图像问题
针对训练1 若将上图中的纵坐标由“x”改为“v”,即如图象所示.
(1)试分析各段的运动情况
(2)画出它的a-t图.
斜率表示加速度
解析
0~2s加速度
2~4s加速度
4~6s加速度
针对训练2 在如图所示的位移(x)—时间(t)图象和速度(v)—时间(t)图象中,给出的四条图线甲、乙、丙、丁分别代表四辆车由同一地点向同一方向运动的情况,则下列说法正确的是( )
A.t1时刻,乙车追上甲车
B.0~t1时间内,甲、乙两车的平均速度相等
C.丙、丁两车在t2时刻相遇
D.0~t2时间内,丙、丁两车的平均速度相等
相遇
△x相同
速度相等
面积表位移
x丙> x丁
AB
课后练习
教P34,“练习与评价”,2题
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
