教科版(2019) 必修 第一册2.4 匀变速直线运动规律的应用 (共19张)PPT
文档属性
| 名称 | 教科版(2019) 必修 第一册2.4 匀变速直线运动规律的应用 (共19张)PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-15 12:27:46 | ||
图片预览






文档简介
(共20张PPT)
1.8 匀变速直线运动规律的应用
飞机跑道的设计(课本P33)
【活动】飞机在跑道上加速滑行时加速度 a1=4.0m/s2,如果当速率达到起飞速率 85m/s时立刻停止起飞,并以大小为a2 = 5.0 m/s2的恒定加速度减速,为确保飞机不滑出跑道,则跑道的长度至少应当设计为多长
·
·
·
飞机的加速阶段:
解:
飞机的减速阶段:
④
③
②
①
由① ~⑤式带入数据解得:
⑤
又有:
以飞机运动方向为正方向,设轨道的最少长度为x,如图所示。则由匀变速直线运动的规律有:
·
·
·
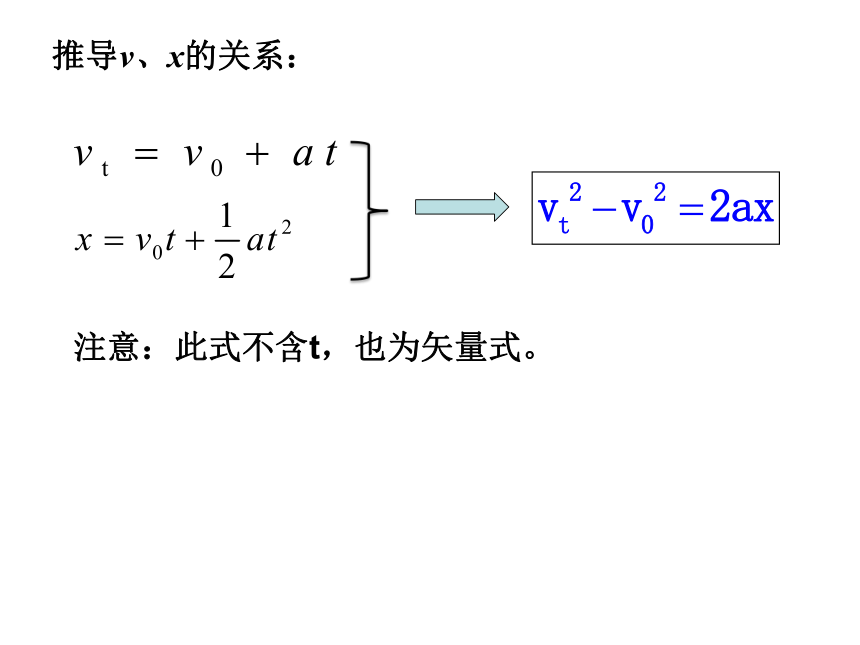
注意:此式不含t,也为矢量式。
推导v、x的关系:
·
·
·
特别注意
:若不含时间t,可用公式
解:
对加速过程有:
对减速过程有:
且
由以上三式代入数据解得:
以飞机运动方向为正方向,设轨道的最少长度为x,如图所示。则由匀变速直线运动的规律有:
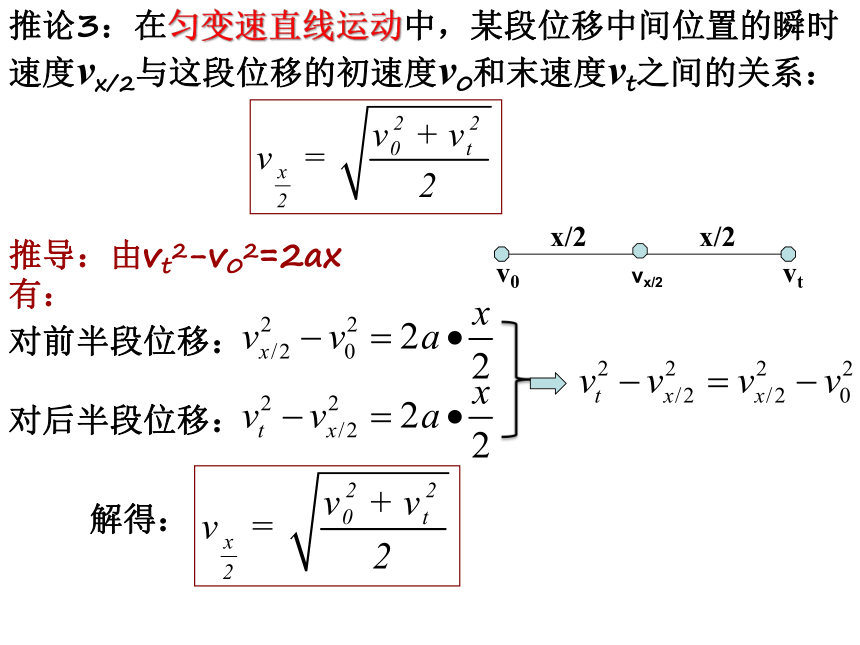
推论3:在匀变速直线运动中,某段位移中间位置的瞬时速度vx/2与这段位移的初速度v0和末速度vt之间的关系:
推导:由vt2-v02=2ax有:
v0
x/2
x/2
vt
vx/2
对前半段位移:
对后半段位移:
解得:
例题:一物体由静止沿光滑斜面匀加速下滑距离为 l 时,速度为 v,当它下滑距离为l / 2时,速度为多少?
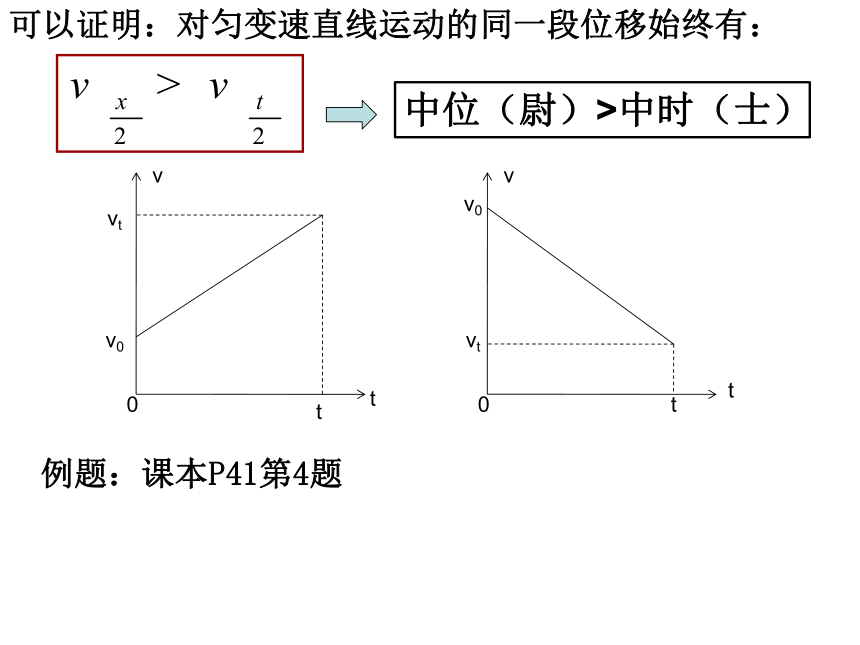
可以证明:对匀变速直线运动的同一段位移始终有:
v
t
0
v0
vt
t
v
t
0
v0
vt
t
中位(尉)>中时(士)
例题:课本P41第4题
匀变速直线运动的几个推论
推论3.在某段时间内中间位置的瞬时速度与这段位移的初末速度的关系为
总结
推论1:物体做匀变速直线运动的初速度为 ,末速度为 ,物体在某段时间t的中间时刻的瞬时速度等于这段时间内的平均速度,即:
推论2:匀变速直线运动,在连续相邻相同时间内的位移之差是定值,即
=
且有xm- xn=(m-n)aT2
推论4 .末速度为零的匀减速直线运动可看成反向的初速度为零,加速度不变的匀加速直线运动。(逆向思维法)
初速度为零的匀变速直线运动的规律
1. 1T末、2T末、3T末…瞬时速度之比为
2. 1T内、2T内、3T内…位移之比为
v1∶v2∶v3∶ ∶ vn=1∶2∶3∶ ∶ n
x1∶x2∶x3∶ ∶ xn=12∶22∶32∶ ∶ n2
4. 通过连续相等的位移所用时间之比为
3. 在第一个T内、第二个T内、第三个T内…位移之比为
xⅠ∶xⅡ∶xⅢ∶ ∶ xn=1∶3∶5∶ ∶(2n-1)
例题:物体从静止开始作匀加速直线运动,则其第1s末的速度与第3秒末的速度之比是 ;第3s内的位移与第5s内的位移之比是 ; 若第1s的位移是3m,则第3s内的位移是 m。
1:3
5:9
15
变式训练(课本P34第1题):一物体做匀减速直线运动,3.5秒后停下来,则第1秒内,第2秒内,第3秒内的位移之比为_________。
3:2:1
巩固练习:
1、一质点做从静止开始做匀加速直线运动,则质点在第一个2s,第二个2s和第5s内的三段位移之比为________。
4:12:9
2、一颗子弹沿水平方向射来, 恰穿透固定在水平面上三块相同的木板,设子弹穿过木板时的加速度恒定,则子弹穿过三块木板所用的时间之比为___________ 。
V0
A
B
C
小结:
1.逆向思维在物理解题中很有用.有些物理问题,若用常规的正向思维方法去思考,往往不易求解,若采用逆向思维去反面推敲,则可使问题得到简明的解答;
2.熟悉推论并能灵活应用它们,即能开拓解题的思路,又能简化解题过程;
3.图像法解题的特点是直观,有些问题借助图像只需简单的计算就能求解;
4.一题多解能训练大家的发散思维,对能力有较高的要求.
《笔记》P25“随堂演练”
(课后作业)3.火车紧急刹车后经7s停止,设火车匀减速直线运动,它在最后1s内的位移是2m,则火车在刹车过程中通过的位移和开始刹车时的速度各是多少?
解法一:用基本公式、平均速度.
解法二:逆向思维,看作初速为0的逆过程
解法三:图像法作出质点的速度-时间图像质点第7s内的位移大小为阴影部分小三角形面积:
答案:98m 28m/s
喷气式飞机制动系统的设计
活动:详见课本P33
活动:估测楼房的高度(课本P34)
为了估测楼房的高度,从楼房顶端使一个小球自由下落,用曝光时间为0.01s的照相机拍摄小球在空中的运动,得到的照片上有一条模糊的径迹,如图所示。用刻度尺量出每块砖的厚度为6cm,径迹的下端B距地面的高度是1.2m,你能估算出楼房的高度吗?
O为楼顶
A
B
1.8 匀变速直线运动规律的应用
飞机跑道的设计(课本P33)
【活动】飞机在跑道上加速滑行时加速度 a1=4.0m/s2,如果当速率达到起飞速率 85m/s时立刻停止起飞,并以大小为a2 = 5.0 m/s2的恒定加速度减速,为确保飞机不滑出跑道,则跑道的长度至少应当设计为多长
·
·
·
飞机的加速阶段:
解:
飞机的减速阶段:
④
③
②
①
由① ~⑤式带入数据解得:
⑤
又有:
以飞机运动方向为正方向,设轨道的最少长度为x,如图所示。则由匀变速直线运动的规律有:
·
·
·
注意:此式不含t,也为矢量式。
推导v、x的关系:
·
·
·
特别注意
:若不含时间t,可用公式
解:
对加速过程有:
对减速过程有:
且
由以上三式代入数据解得:
以飞机运动方向为正方向,设轨道的最少长度为x,如图所示。则由匀变速直线运动的规律有:
推论3:在匀变速直线运动中,某段位移中间位置的瞬时速度vx/2与这段位移的初速度v0和末速度vt之间的关系:
推导:由vt2-v02=2ax有:
v0
x/2
x/2
vt
vx/2
对前半段位移:
对后半段位移:
解得:
例题:一物体由静止沿光滑斜面匀加速下滑距离为 l 时,速度为 v,当它下滑距离为l / 2时,速度为多少?
可以证明:对匀变速直线运动的同一段位移始终有:
v
t
0
v0
vt
t
v
t
0
v0
vt
t
中位(尉)>中时(士)
例题:课本P41第4题
匀变速直线运动的几个推论
推论3.在某段时间内中间位置的瞬时速度与这段位移的初末速度的关系为
总结
推论1:物体做匀变速直线运动的初速度为 ,末速度为 ,物体在某段时间t的中间时刻的瞬时速度等于这段时间内的平均速度,即:
推论2:匀变速直线运动,在连续相邻相同时间内的位移之差是定值,即
=
且有xm- xn=(m-n)aT2
推论4 .末速度为零的匀减速直线运动可看成反向的初速度为零,加速度不变的匀加速直线运动。(逆向思维法)
初速度为零的匀变速直线运动的规律
1. 1T末、2T末、3T末…瞬时速度之比为
2. 1T内、2T内、3T内…位移之比为
v1∶v2∶v3∶ ∶ vn=1∶2∶3∶ ∶ n
x1∶x2∶x3∶ ∶ xn=12∶22∶32∶ ∶ n2
4. 通过连续相等的位移所用时间之比为
3. 在第一个T内、第二个T内、第三个T内…位移之比为
xⅠ∶xⅡ∶xⅢ∶ ∶ xn=1∶3∶5∶ ∶(2n-1)
例题:物体从静止开始作匀加速直线运动,则其第1s末的速度与第3秒末的速度之比是 ;第3s内的位移与第5s内的位移之比是 ; 若第1s的位移是3m,则第3s内的位移是 m。
1:3
5:9
15
变式训练(课本P34第1题):一物体做匀减速直线运动,3.5秒后停下来,则第1秒内,第2秒内,第3秒内的位移之比为_________。
3:2:1
巩固练习:
1、一质点做从静止开始做匀加速直线运动,则质点在第一个2s,第二个2s和第5s内的三段位移之比为________。
4:12:9
2、一颗子弹沿水平方向射来, 恰穿透固定在水平面上三块相同的木板,设子弹穿过木板时的加速度恒定,则子弹穿过三块木板所用的时间之比为___________ 。
V0
A
B
C
小结:
1.逆向思维在物理解题中很有用.有些物理问题,若用常规的正向思维方法去思考,往往不易求解,若采用逆向思维去反面推敲,则可使问题得到简明的解答;
2.熟悉推论并能灵活应用它们,即能开拓解题的思路,又能简化解题过程;
3.图像法解题的特点是直观,有些问题借助图像只需简单的计算就能求解;
4.一题多解能训练大家的发散思维,对能力有较高的要求.
《笔记》P25“随堂演练”
(课后作业)3.火车紧急刹车后经7s停止,设火车匀减速直线运动,它在最后1s内的位移是2m,则火车在刹车过程中通过的位移和开始刹车时的速度各是多少?
解法一:用基本公式、平均速度.
解法二:逆向思维,看作初速为0的逆过程
解法三:图像法作出质点的速度-时间图像质点第7s内的位移大小为阴影部分小三角形面积:
答案:98m 28m/s
喷气式飞机制动系统的设计
活动:详见课本P33
活动:估测楼房的高度(课本P34)
为了估测楼房的高度,从楼房顶端使一个小球自由下落,用曝光时间为0.01s的照相机拍摄小球在空中的运动,得到的照片上有一条模糊的径迹,如图所示。用刻度尺量出每块砖的厚度为6cm,径迹的下端B距地面的高度是1.2m,你能估算出楼房的高度吗?
O为楼顶
A
B
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
