教科版(2019)必修 第一册 2.2匀变速直线运动的速度与时间的关系PPT(共17张)
文档属性
| 名称 | 教科版(2019)必修 第一册 2.2匀变速直线运动的速度与时间的关系PPT(共17张) |  | |
| 格式 | zip | ||
| 文件大小 | 439.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-15 12:28:14 | ||
图片预览




文档简介
(共17张PPT)
2.2 匀变速直线运动速度时间关系
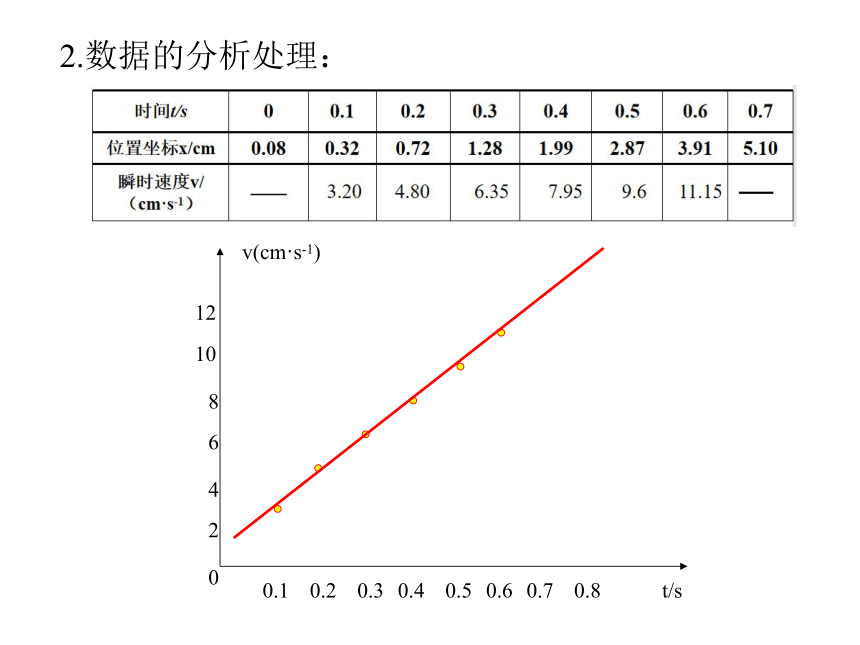
1.取与某点相邻的两个计数点间的平均速度为该点的瞬时速度,并填在下表中:
时间t/s 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
位置坐标x/cm 0.08 0.32 0.72 1.28 1.99 2.87 3.91 5.10
瞬时速度v/(cm·s-1) ——
3.20
4.80
6.35
7.95
9.6
11.15
频闪摄影技术
0
2
4
6
8
10
12
t/s
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
v(cm·s-1)
2.数据的分析处理:
v/m/s
0
t/s
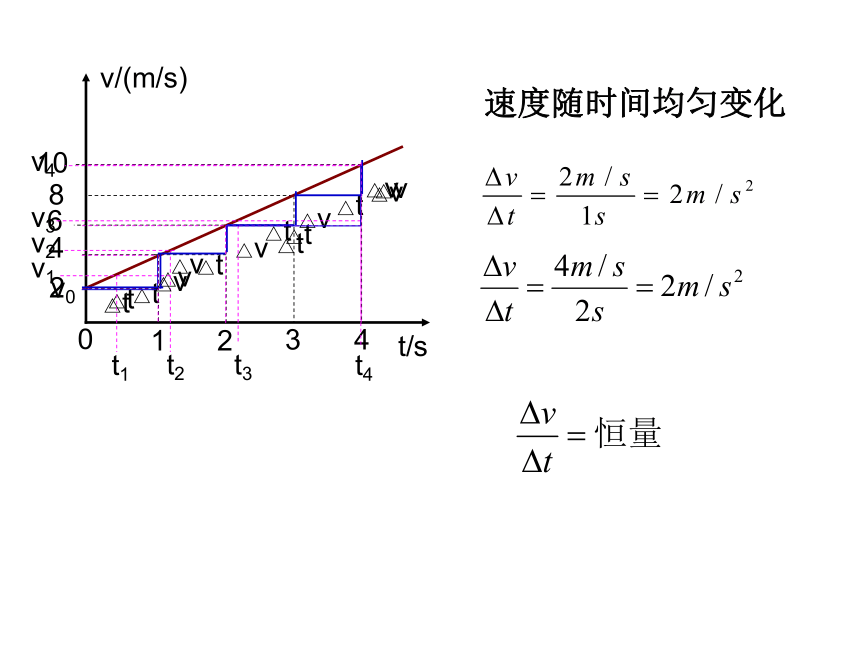
物体的速度随时间怎样变化?物体做什么样的运动?
△t
△v
△t
△v
△v
△v
△t
△t
4
6
8
10
1
2
3
4
v0
v/(m/s)
t/s
0
t1
t2
t4
t3
△t
△t
△v
△v
v1
v2
v3
v4
2
△t
△v
△t
△v
速度随时间均匀变化
1.定义:速度随时间均匀变化即加速度恒定的直线运动,称为匀变速直线运动.
(匀变速直线运动的v-t图象是一条倾斜的直线)
2.分类:
匀加速直线运动:
物体的速度随时间均匀增加。
匀减速直线运动:
物体的速度随时间均匀减小。
一、匀变速直线运动
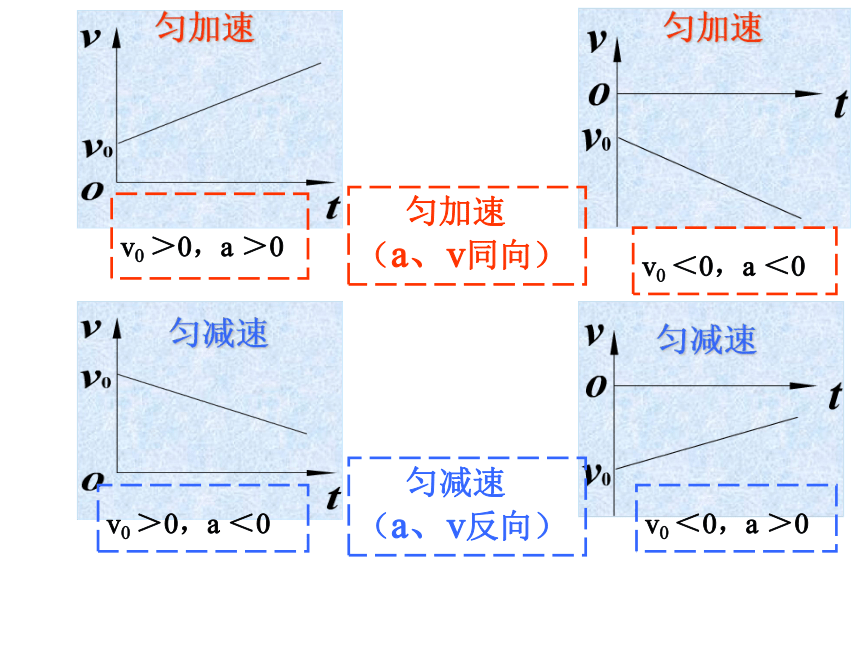
v0 >0,a >0
v0 <0,a <0
匀加速
(a、v同向)
匀减速
(a、v反向)
v0 <0,a >0
v0 >0,a <0
匀加速
匀加速
匀减速
匀减速
v
0
t
v0
t
v
t
v
0
Δv=at
v0
1.公式的推导:
V=V0+at
二、匀变速直线运动速度时间关系
①.从图象上看V与t的关系如
右图所示:
②.根据加速度的定义式:
v= v0 + at
△v
a = ——
△t
= ———
v- v0
t
△v = a t
v = v0 + a t
①.公式的矢量性
②.公式的适用条件
只适用于匀变速直线运动.
2.关系式的理解
应先规定正方向,一般以v0的方向为正方向.
③.公式的特殊形式
(1)当a=0时,vt=v0(匀速直线运动).
(2)当v0=0时,vt=at(由静止开始的匀加速直线运动).
例题1、汽车以36km/h的速度匀速行驶,现以0.6m/s2的加速度加速,10s后速度能达到多少?
运动示意图
解:以初速度v0=36km/h=10m/s的方向为正方向
则10s后的速度:
v=v0+at
=10m/s+0.6m/s2×10s
=16m/s
例题2、某汽车在某路面紧急刹车时,加速度的大小是6m/s2,如果必须在2s内停下来,汽车的行驶速度最高不能超过多少?
运动示意图
解:以汽车初速度v0方向为正方向
则由v=v0+at得
v0=v-at=0 - ( -6m/s2)×2s=12m/s=43km/h
汽车的速度不能超过43km/h
解答1:
刹车后3s末的速度 v3=v0+at=20m/s+4.0×3m/s=32m/s
6s末的速度v6=v0+at=20m/s+4.0×6m/s=44m/s
例题3 :汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
运动示意图
解答2:
以初速度v0=20m/s的方向为正方向
则加速度a=﹣4.0m/s2,
刹车后3s末的速度 v3=v0+at=20m/s﹣4.0×3m/s=8m/s
6s末的速度
v6=v0+at=20m/s﹣4.0×6m/s=-4m/s
例题3 :汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
运动示意图
解:由题以初速度v0=20m/s的方向为正方向,
则加速度a=﹣4.0m/s2,
刹车至停止所需时间
t=(vt﹣v0)/a=(0﹣20m/s)/(﹣4.0m/s2)=5s。
故刹车后3s时的速度v3=v0+at=20m/s﹣4.0m/s2×3s=8m/s
刹车后6s时汽车已停止运动,故v6=0
例题3 :汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
注意:
v = v0 + a t
1、该式是矢量式(应用时要先规定正方向);
2、刹车问题要先判断停止时间。
小结
一、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动 叫做匀变速直线运动
2、分类:
匀加速直线运动
匀减速直线运动
二、匀变速直线运动的速度与时间关系式
V = V0 + at
2.2 匀变速直线运动速度时间关系
1.取与某点相邻的两个计数点间的平均速度为该点的瞬时速度,并填在下表中:
时间t/s 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
位置坐标x/cm 0.08 0.32 0.72 1.28 1.99 2.87 3.91 5.10
瞬时速度v/(cm·s-1) ——
3.20
4.80
6.35
7.95
9.6
11.15
频闪摄影技术
0
2
4
6
8
10
12
t/s
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
v(cm·s-1)
2.数据的分析处理:
v/m/s
0
t/s
物体的速度随时间怎样变化?物体做什么样的运动?
△t
△v
△t
△v
△v
△v
△t
△t
4
6
8
10
1
2
3
4
v0
v/(m/s)
t/s
0
t1
t2
t4
t3
△t
△t
△v
△v
v1
v2
v3
v4
2
△t
△v
△t
△v
速度随时间均匀变化
1.定义:速度随时间均匀变化即加速度恒定的直线运动,称为匀变速直线运动.
(匀变速直线运动的v-t图象是一条倾斜的直线)
2.分类:
匀加速直线运动:
物体的速度随时间均匀增加。
匀减速直线运动:
物体的速度随时间均匀减小。
一、匀变速直线运动
v0 >0,a >0
v0 <0,a <0
匀加速
(a、v同向)
匀减速
(a、v反向)
v0 <0,a >0
v0 >0,a <0
匀加速
匀加速
匀减速
匀减速
v
0
t
v0
t
v
t
v
0
Δv=at
v0
1.公式的推导:
V=V0+at
二、匀变速直线运动速度时间关系
①.从图象上看V与t的关系如
右图所示:
②.根据加速度的定义式:
v= v0 + at
△v
a = ——
△t
= ———
v- v0
t
△v = a t
v = v0 + a t
①.公式的矢量性
②.公式的适用条件
只适用于匀变速直线运动.
2.关系式的理解
应先规定正方向,一般以v0的方向为正方向.
③.公式的特殊形式
(1)当a=0时,vt=v0(匀速直线运动).
(2)当v0=0时,vt=at(由静止开始的匀加速直线运动).
例题1、汽车以36km/h的速度匀速行驶,现以0.6m/s2的加速度加速,10s后速度能达到多少?
运动示意图
解:以初速度v0=36km/h=10m/s的方向为正方向
则10s后的速度:
v=v0+at
=10m/s+0.6m/s2×10s
=16m/s
例题2、某汽车在某路面紧急刹车时,加速度的大小是6m/s2,如果必须在2s内停下来,汽车的行驶速度最高不能超过多少?
运动示意图
解:以汽车初速度v0方向为正方向
则由v=v0+at得
v0=v-at=0 - ( -6m/s2)×2s=12m/s=43km/h
汽车的速度不能超过43km/h
解答1:
刹车后3s末的速度 v3=v0+at=20m/s+4.0×3m/s=32m/s
6s末的速度v6=v0+at=20m/s+4.0×6m/s=44m/s
例题3 :汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
运动示意图
解答2:
以初速度v0=20m/s的方向为正方向
则加速度a=﹣4.0m/s2,
刹车后3s末的速度 v3=v0+at=20m/s﹣4.0×3m/s=8m/s
6s末的速度
v6=v0+at=20m/s﹣4.0×6m/s=-4m/s
例题3 :汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
运动示意图
解:由题以初速度v0=20m/s的方向为正方向,
则加速度a=﹣4.0m/s2,
刹车至停止所需时间
t=(vt﹣v0)/a=(0﹣20m/s)/(﹣4.0m/s2)=5s。
故刹车后3s时的速度v3=v0+at=20m/s﹣4.0m/s2×3s=8m/s
刹车后6s时汽车已停止运动,故v6=0
例题3 :汽车以20m/s的速度匀速行驶,现以4.0m/s2的加速度开始刹车,则刹车后3s末和6s末的速度各是多少?
注意:
v = v0 + a t
1、该式是矢量式(应用时要先规定正方向);
2、刹车问题要先判断停止时间。
小结
一、匀变速直线运动
1、定义:沿着一条直线,且加速度不变的运动 叫做匀变速直线运动
2、分类:
匀加速直线运动
匀减速直线运动
二、匀变速直线运动的速度与时间关系式
V = V0 + at
同课章节目录
- 第一章 描述运动的基本概念
- 1 参考系 时间 质点
- 2 位置 位移
- 3 位置变化的快慢与方向——速度
- 4 实验:用打点计时器测量小车的速度
- 5 速度变化的快慢与方向——加速度
- 第二章 匀变速直线运动的规律
- 1 匀变速直线运动的研究
- 2 匀变速直线运动速度与时间的关系
- 3 匀变速直线运动位移与时间的关系
- 4 匀变速直线运动规律的应用
- 5 自由落体运动
- 第三章 相互作用
- 1 力 重力
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 6 共点力作用下物体的平衡
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 牛顿运动定律的应用
- 7 超重与失重
