苏教版(2019)高中数学必修第一册 《6.3对数函数》精品课件(共19张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 《6.3对数函数》精品课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 16:46:03 | ||
图片预览





文档简介
(共19张PPT)
苏教版同步教材精品课件
6.3 对数函数
情境引入
拉面模型:厨师在拉面时,由1根拉成2根,2根拉成4根,4根拉成8根……试写出1根这样的面拉y次得到x根面条的关系式
问题:根据对数的定义,这个关系式写成对数式的形式是什么?
这个函数就是我们今天所要研究的对数函数.
情境引入
1.对数函数的定义:一般地,函数叫作对数函数,它的定义域是.
需要注意的是:①底数a是一个大于0且不等于1的常数:②自变量x在真数的位置上;③对数符号前面的系数为1.
2.练习:判断下列函数是否为对数函数,并说明理由:
(1):(2);(3);
(4) ;(5);(6).
注意:对数函数的定义与指数函数类似,都是形式定义,注意辨别.
探究一 对数函数的图象与性质
下面画出了函数和的图象:
探究新知
根据上面图象,结合指数函数的性质,归纳出对数函数的性质:
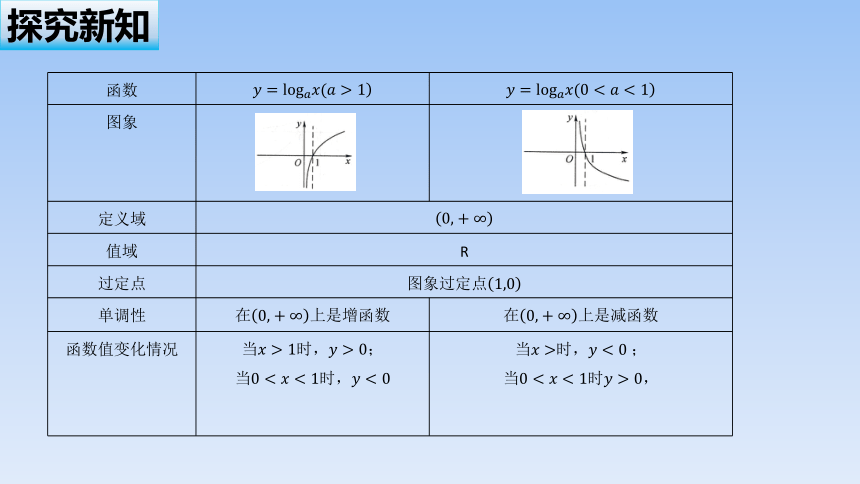
探究新知
函数
图象
定义域
值域 R
过定点 图象过定点
单调性 在上是增函数 在上是减函数
函数值变化情况 当时,; 当时, 当时, ;
当时,
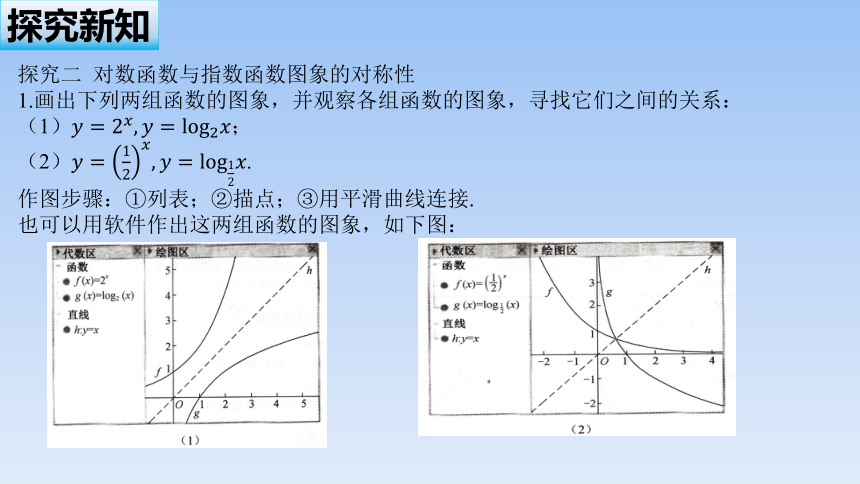
探究二 对数函数与指数函数图象的对称性
1.画出下列两组函数的图象,并观察各组函数的图象,寻找它们之间的关系:
(1);
(2).
作图步骤:①列表;②描点;③用平滑曲线连接.
也可以用软件作出这两组函数的图象,如下图:
探究新知
以(1)和的图象(如图)为例:
探究新知
思考1:直观感受:这两个函数图象之间有什么关系?
思考2:取指数函数图象上的点,在对数函数图象上有点 ,两组点有什么关系?
思考3:任取指数函数图象上一点,在对数函数图象上的对称点是什么?
思考4:类比以2为底的对数函数和指数函数图象关系,以为底的对数函数与指数函数图象之间是否也存在类似的关系?
探究新知
思考5:对另一组函数和是否也有类似的结论呢?
思考6:一般地,当时,函数与的图象有怎样的关系?
小结:同底数的对数函数与指数函数的图象关于直线对称.
设计意图:发现数学中图象的对称美.在学习数学的过程中,不只有枯燥的计算和逻辑推理,也存在许多美丽的图象,这也是数学的魅力之一.
探究新知
2.观察分别以2和为底的两组对数函数和指数函数图象(如图):
结论:当时,称为的反函数,反之,也称为的反函数.一般地,如果函数存在反函数,那么它的反函数记作.
3.思考:底数互为倒数的指数函数图象关于y轴对称,那么在对数函数当中是否也有类似的性质呢?
(几何画板演示)
结论:底数互为倒数的对数函数图象关于x轴对称.
探究三 不同底数的对数函数图象
函数图象如图所示试说明哪个函数对应于哪个图象,并解释为什么.
探究新知
(学生自由讨论,教师点评学生思考讨论的结果)
方法:可通过找特征点来判断函数图象位置.
思考1:函数和的图象如何确定?
思考2:在第一象限内,随着底数的变化,这四个对数函数图象有什么变化趋势?
小结:在第一象限内,随着底数的增大,对数函数图象以为支点顺时针靠近x轴.
(几何画板演示在第一象限内,函数图象随底数的变化而变化的情况)
设计意图:注重引导学生用从特殊到一般的方法探究对数函数图象的形成过程,进一步体会函数作图的一般方法.同时,启发学生通过对数与指数的关系将对数函数的图象转化为指数函数的图象,体会数学知识间的相互联系以及转化的思想方法,拓宽学生探究的思路和方法,提高探究的效率和质量.教师还可通过信息技术增强学生的直观感受,发挥多元表征的作用.
典例剖析
例1、求下列函数的定义域:
(1);
(2).
解析
(1)当,即时,有意义;
当时,没有意义.
因此,函数的定义域是.
(2)当,即时,有意义;
当时,没有意义.
因此,函数的定义域是.
小结:求函数的定义域的本质是解不等式或不等式组此题只是对数函数性质的简单应用,应强调学生注意书写格式.
典例剖析
例2、比较下列各组数中两个数的大小:
(1);
(2);
(3).
解析
(1)考察对数函数.
因为,
所以在区间上是增函数.
又因为,
所以.
(2)考察对数函数.
因为,
所以在区间上是减函数.
又因为,
所以.
典例剖析
例2、比较下列各组数中两个数的大小:
(1);
(2);
(3).
解析
(3)考察对数函数.
因为,
所以在区间上是增函数.
又因为,
所以.
同理,
所以.
小结:1.两个同底数的对数比较大小的一般步骤:
(1)确定所要考察的对数函数;
(2)根据对数底数判断对数函数的单调性;
(3)比较真数大小,然后利用对数函数的单调性判断两个对数值的大小.
2.两个不同底数的对数比较大小,一般取“1”或其他相关数值作为中间值帮助比较.
典例剖析
例3、说明函数与函数的图象的关系.
解析
比较函数与的取值关系,列表如下表所示.
一般地,函数中对应的y值与函数中对应的y值相等,则将对数函数的图象向左平移2个单位长度,就得到函数的图象.
典例剖析
例3、说明函数与函数的图象的关系.
解析
这两个函数的图象如图所示.
典例剖析
思考:函数与函数的图象之间有怎样的关系?
一般地,当时,将的图象向左平移b个单位就可得到函数的图象;当时,将的图象向右平移个单位就可得到函数的图象.
典例剖析
例4、画出函数的图象,并根据图象写出函数的单调区间.
解析
由于函数满足对任意的都有,
所以函数是偶函数,它的图象关于y轴对称.
当时,.因此,我们先画出函数的图象,再作出关于y轴对称的图象和构成函数的图象,如图所示.
由图象可以知道,函数的减区间是,增区间是.
课堂小结
1.在知识方面:
(1)学习了对数函数的概念、图象及性质.
(2)会应用对数函数的知识求定义域.
(3)会利用对数函数单调性比较两个对数的大小.
(4)会根据平移变换得到的图象.
2.思想方法方面:体会了类比、由特殊到一般、分类与整合、分类讨论的思想方法.
作 业
教材第148页练习第2,3,4题.
苏教版同步教材精品课件
6.3 对数函数
情境引入
拉面模型:厨师在拉面时,由1根拉成2根,2根拉成4根,4根拉成8根……试写出1根这样的面拉y次得到x根面条的关系式
问题:根据对数的定义,这个关系式写成对数式的形式是什么?
这个函数就是我们今天所要研究的对数函数.
情境引入
1.对数函数的定义:一般地,函数叫作对数函数,它的定义域是.
需要注意的是:①底数a是一个大于0且不等于1的常数:②自变量x在真数的位置上;③对数符号前面的系数为1.
2.练习:判断下列函数是否为对数函数,并说明理由:
(1):(2);(3);
(4) ;(5);(6).
注意:对数函数的定义与指数函数类似,都是形式定义,注意辨别.
探究一 对数函数的图象与性质
下面画出了函数和的图象:
探究新知
根据上面图象,结合指数函数的性质,归纳出对数函数的性质:
探究新知
函数
图象
定义域
值域 R
过定点 图象过定点
单调性 在上是增函数 在上是减函数
函数值变化情况 当时,; 当时, 当时, ;
当时,
探究二 对数函数与指数函数图象的对称性
1.画出下列两组函数的图象,并观察各组函数的图象,寻找它们之间的关系:
(1);
(2).
作图步骤:①列表;②描点;③用平滑曲线连接.
也可以用软件作出这两组函数的图象,如下图:
探究新知
以(1)和的图象(如图)为例:
探究新知
思考1:直观感受:这两个函数图象之间有什么关系?
思考2:取指数函数图象上的点,在对数函数图象上有点 ,两组点有什么关系?
思考3:任取指数函数图象上一点,在对数函数图象上的对称点是什么?
思考4:类比以2为底的对数函数和指数函数图象关系,以为底的对数函数与指数函数图象之间是否也存在类似的关系?
探究新知
思考5:对另一组函数和是否也有类似的结论呢?
思考6:一般地,当时,函数与的图象有怎样的关系?
小结:同底数的对数函数与指数函数的图象关于直线对称.
设计意图:发现数学中图象的对称美.在学习数学的过程中,不只有枯燥的计算和逻辑推理,也存在许多美丽的图象,这也是数学的魅力之一.
探究新知
2.观察分别以2和为底的两组对数函数和指数函数图象(如图):
结论:当时,称为的反函数,反之,也称为的反函数.一般地,如果函数存在反函数,那么它的反函数记作.
3.思考:底数互为倒数的指数函数图象关于y轴对称,那么在对数函数当中是否也有类似的性质呢?
(几何画板演示)
结论:底数互为倒数的对数函数图象关于x轴对称.
探究三 不同底数的对数函数图象
函数图象如图所示试说明哪个函数对应于哪个图象,并解释为什么.
探究新知
(学生自由讨论,教师点评学生思考讨论的结果)
方法:可通过找特征点来判断函数图象位置.
思考1:函数和的图象如何确定?
思考2:在第一象限内,随着底数的变化,这四个对数函数图象有什么变化趋势?
小结:在第一象限内,随着底数的增大,对数函数图象以为支点顺时针靠近x轴.
(几何画板演示在第一象限内,函数图象随底数的变化而变化的情况)
设计意图:注重引导学生用从特殊到一般的方法探究对数函数图象的形成过程,进一步体会函数作图的一般方法.同时,启发学生通过对数与指数的关系将对数函数的图象转化为指数函数的图象,体会数学知识间的相互联系以及转化的思想方法,拓宽学生探究的思路和方法,提高探究的效率和质量.教师还可通过信息技术增强学生的直观感受,发挥多元表征的作用.
典例剖析
例1、求下列函数的定义域:
(1);
(2).
解析
(1)当,即时,有意义;
当时,没有意义.
因此,函数的定义域是.
(2)当,即时,有意义;
当时,没有意义.
因此,函数的定义域是.
小结:求函数的定义域的本质是解不等式或不等式组此题只是对数函数性质的简单应用,应强调学生注意书写格式.
典例剖析
例2、比较下列各组数中两个数的大小:
(1);
(2);
(3).
解析
(1)考察对数函数.
因为,
所以在区间上是增函数.
又因为,
所以.
(2)考察对数函数.
因为,
所以在区间上是减函数.
又因为,
所以.
典例剖析
例2、比较下列各组数中两个数的大小:
(1);
(2);
(3).
解析
(3)考察对数函数.
因为,
所以在区间上是增函数.
又因为,
所以.
同理,
所以.
小结:1.两个同底数的对数比较大小的一般步骤:
(1)确定所要考察的对数函数;
(2)根据对数底数判断对数函数的单调性;
(3)比较真数大小,然后利用对数函数的单调性判断两个对数值的大小.
2.两个不同底数的对数比较大小,一般取“1”或其他相关数值作为中间值帮助比较.
典例剖析
例3、说明函数与函数的图象的关系.
解析
比较函数与的取值关系,列表如下表所示.
一般地,函数中对应的y值与函数中对应的y值相等,则将对数函数的图象向左平移2个单位长度,就得到函数的图象.
典例剖析
例3、说明函数与函数的图象的关系.
解析
这两个函数的图象如图所示.
典例剖析
思考:函数与函数的图象之间有怎样的关系?
一般地,当时,将的图象向左平移b个单位就可得到函数的图象;当时,将的图象向右平移个单位就可得到函数的图象.
典例剖析
例4、画出函数的图象,并根据图象写出函数的单调区间.
解析
由于函数满足对任意的都有,
所以函数是偶函数,它的图象关于y轴对称.
当时,.因此,我们先画出函数的图象,再作出关于y轴对称的图象和构成函数的图象,如图所示.
由图象可以知道,函数的减区间是,增区间是.
课堂小结
1.在知识方面:
(1)学习了对数函数的概念、图象及性质.
(2)会应用对数函数的知识求定义域.
(3)会利用对数函数单调性比较两个对数的大小.
(4)会根据平移变换得到的图象.
2.思想方法方面:体会了类比、由特殊到一般、分类与整合、分类讨论的思想方法.
作 业
教材第148页练习第2,3,4题.
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
