苏教版(2019)高中数学必修第二册 13.2.2空间两条直线的位置关系课件(共29张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 13.2.2空间两条直线的位置关系课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 945.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 16:55:01 | ||
图片预览








文档简介
(共29张PPT)
13.2.2 空间两条直线的位置关系
问题 六角螺母中直线AB与CD的位置关系是什么?
CD与BE的位置关系是什么?
提示 是异面直线;是平行直线.
情景引入
内
容
索
引
知识梳理
题型探究
检测反馈
1
知识梳理
PART ONE
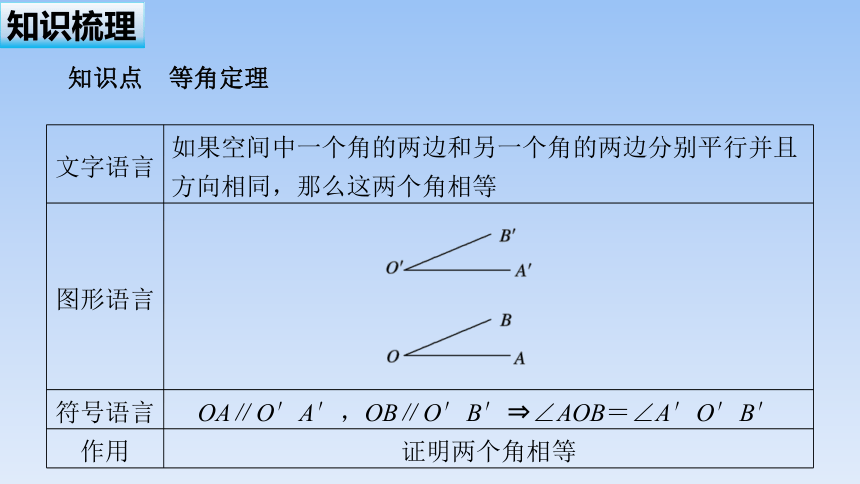
知识点 等角定理
文字语言 如果空间中一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等
图形语言
符号语言 OA∥O′A′,OB∥O′B′ ∠AOB=∠A′O′B′
作用 证明两个角相等
知识梳理
知识点 异面直线的判断
方法 内容
定义法 不同在任何一个平面内的两条直线叫作异面直线
定理法 过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线
反证法 判定两条直线既不平行也不相交,那么这两条直线就是异面直线
知识梳理
2
题型探究
PART ONE
例1 如图,已知在棱长为a的正方体ABCD—A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:四边形MNA1C1是梯形.
一、平行线的传递性
题型探究
证明 如图 ,连接AC,在△ACD中,
∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,
由正方体的性质,得AC∥A1C1,且AC=A1C1.
即MN≠A1C1,
∴四边形MNA1C1是梯形.
题型探究
二、等角定理的应用
题型探究
∴AB∥A′B′,同理AC∥A′C′,BC∥B′C′.
∵A′B′∥AB,A′C′∥AC,
∴∠BAC=∠B'A′C′,
同理∠ABC=∠A′B′C′,
题型探究
(2)如图所示,在正方体ABCD-A1B1C1D1中,E,E1分别是棱AD,A1D1的中点.求证:∠BEC=∠B1E1C1.
题型探究
证明 如图,连接EE1.∵E1,E分别为A1D1,AD的中点,
∴A1E1∥AE,且 A1E1=AE ,
∴四边形A1E1EA为平行四边形,
∴A1A∥E1E,且A1A=E1E,
又A1A∥B1B, 且A1A=B1B, ∴E1E∥B1B,E1E=B1B,
∴四边形E1EBB1是平行四边形.
∴E1B1∥EB.同理E1C1∥EC.
即∠B1E1C1与∠BEC的两边分别对应平行且方向相同,
∴∠B1E1C1=∠BEC.
题型探究
若空间中一个角的两边和另一个角的两边分别平行,则这两个角相等或互补,在实际应用时一般是借助于图形判断是相等还是互补,还是两种情况都有可能.
反思感悟
例3 (1)在四棱锥P—ABCD中,各棱所在的直线互为异面的有____对.
三、异面直线的判断
8
解析 与AB异面的有侧棱PD和PC,
同理,与底面的各条边异面的侧棱都有两条,
故共有异面直线4×2=8(对).
题型探究
(2)如图是一个正方体的展开图,如果将它还原成正方体,那么AB,CD,EF,GH这四条线段所在的直线是异面直线的有几对?分别是哪几对?
解 三对,分别为AB与CD,AB与GH,EF与GH.
还原的正方体如图所示.
题型探究
判定异面直线的方法
(1)定义法:利用异面直线的定义,说明两条直线不平行,也不相交,即不可能同在一个平面内.
(2)利用异面直线的判定定理.
(3)反证法:假设两条直线不是异面直线,根据空间两条直线的位置关系,这两条直线一定共面,即可能相交或平行,然后推出矛盾即可.
反思感悟
四、异面直线所成的角
例4 如图,在正方体ABCD-EFGH中,O为侧面ADHE的中心,求:
(1)BE与CG所成的角的大小;
解 ∵CG∥FB,
∴∠EBF是异面直线BE与CG所成的角.
在Rt△EFB中,EF=FB,
∴BE与CG所成的角为45°.
∴∠EBF=45°,
题型探究
(2)FO与BD所成的角的大小.
题型探究
解 如图,连接FH,
∵FB∥AE,FB=AE,AE∥HD,AE=HD,
∴FB=HD,FB∥HD,
∴四边形FBDH是平行四边形,
∴BD∥FH,
∴∠HFO是FO与BD所成的角,
连接HA,AF,则△AFH是等边三角形,
又O是AH的中点,∴∠HFO=30°,
∴FO与BD所成的角为30°.
题型探究
延伸探究
在本例中,若P是平面EFGH的中心,其他条件不变,求OP和CD所成的角.
解 如图,连接EG,HF,
则P为HF的中点,
连接AF,AH,则OP∥AF,
又CD∥AB,
∴∠BAF(或其补角)为异面直线OP与CD所成的角,
∵△ABF是等腰直角三角形,∴∠BAF=45°,
∴OP与CD所成的角为45°.
题型探究
求异面直线所成的角的步骤
(1)找出(或作出)适合题设的角——用平移法,若题设中有中点,常考虑中位线;若异面直线依附于某几何体,且对异面直线平移有困难时,可利用该几何体的特殊点,将异面直线转化为相交直线.
(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.
(3)结论——设由(2)所求得的角的大小为θ.若0°<θ≤90°,则θ为所求;若90°<θ<180°,则180°-θ为所求.
反思感悟
3
检测反馈
PART THREE
1.若一个角的两边分别和另一个角的两边平行,那么这两个角
A.相等 B.互补
C.相等或互补 D.无法确定
√
解析 一个角的两边分别和另一个角的两边平行,那么这两个角相等或互补.
检测反馈
2.直线a与直线b相交,直线c也与直线b相交,则直线a与直线c的位置关系是
A.相交 B.平行 C.异面 D.以上都有可能
√
解析 如图所示,长方体ABCD-A1B1C1D1中,AB与AA1相交,A1B1与AA1相交,AB∥A1B1;
AD与AA1相交,AB与AD相交,AA1与AB相交;
A1D1与AA1相交,AB与AA1相交,AB与A1D1异面.
检测反馈
3.(多选)如图所示,G,H,M,N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有
√
√
检测反馈
解析 A中,直线GH∥MN;
B中,G,H,N三点共面,但M 平面GHN,且N GH,
因此直线GH与MN异面;
C中,连接MG(图略),GM∥HN,
因此,GH与MN共面;
D中,G,M,N三点共面,但H 平面GMN,且G MN,
所以GH与MN异面.
检测反馈
4.如图,在正方体ABCD-A′B′C′D′中,异面直线A′B′与BC所成的角的大小为________.异面直线AD′与BC所成的角的大小为________.
90°
45°
解析 ∵BC∥B′C′,∴∠A′B′C′即异面直线A′B′与BC所成的角,且∠A′B′C′=90°,又BC∥AD,
∴∠D′AD是异面直线AD′与BC所成的角,且∠D′AD=45°.
检测反馈
5.如图,在三棱锥A-BCD中,E,F,G分别是AB,BC,AD的中点,∠GEF=120°,则BD与AC所成的角的大小为________.
60°
解析 依题意知,EG∥BD,EF∥AC,
所以∠GEF(或其补角)即为异面直线AC与BD所成的角,
又∠GEF=120°,
所以异面直线BD与AC所成的角为60°.
检测反馈
13.2.2 空间两条直线的位置关系
问题 六角螺母中直线AB与CD的位置关系是什么?
CD与BE的位置关系是什么?
提示 是异面直线;是平行直线.
情景引入
内
容
索
引
知识梳理
题型探究
检测反馈
1
知识梳理
PART ONE
知识点 等角定理
文字语言 如果空间中一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等
图形语言
符号语言 OA∥O′A′,OB∥O′B′ ∠AOB=∠A′O′B′
作用 证明两个角相等
知识梳理
知识点 异面直线的判断
方法 内容
定义法 不同在任何一个平面内的两条直线叫作异面直线
定理法 过平面内一点与平面外一点的直线,和这个平面内不经过该点的直线是异面直线
反证法 判定两条直线既不平行也不相交,那么这两条直线就是异面直线
知识梳理
2
题型探究
PART ONE
例1 如图,已知在棱长为a的正方体ABCD—A1B1C1D1中,M,N分别是棱CD,AD的中点.求证:四边形MNA1C1是梯形.
一、平行线的传递性
题型探究
证明 如图 ,连接AC,在△ACD中,
∵M,N分别是CD,AD的中点,
∴MN是△ACD的中位线,
由正方体的性质,得AC∥A1C1,且AC=A1C1.
即MN≠A1C1,
∴四边形MNA1C1是梯形.
题型探究
二、等角定理的应用
题型探究
∴AB∥A′B′,同理AC∥A′C′,BC∥B′C′.
∵A′B′∥AB,A′C′∥AC,
∴∠BAC=∠B'A′C′,
同理∠ABC=∠A′B′C′,
题型探究
(2)如图所示,在正方体ABCD-A1B1C1D1中,E,E1分别是棱AD,A1D1的中点.求证:∠BEC=∠B1E1C1.
题型探究
证明 如图,连接EE1.∵E1,E分别为A1D1,AD的中点,
∴A1E1∥AE,且 A1E1=AE ,
∴四边形A1E1EA为平行四边形,
∴A1A∥E1E,且A1A=E1E,
又A1A∥B1B, 且A1A=B1B, ∴E1E∥B1B,E1E=B1B,
∴四边形E1EBB1是平行四边形.
∴E1B1∥EB.同理E1C1∥EC.
即∠B1E1C1与∠BEC的两边分别对应平行且方向相同,
∴∠B1E1C1=∠BEC.
题型探究
若空间中一个角的两边和另一个角的两边分别平行,则这两个角相等或互补,在实际应用时一般是借助于图形判断是相等还是互补,还是两种情况都有可能.
反思感悟
例3 (1)在四棱锥P—ABCD中,各棱所在的直线互为异面的有____对.
三、异面直线的判断
8
解析 与AB异面的有侧棱PD和PC,
同理,与底面的各条边异面的侧棱都有两条,
故共有异面直线4×2=8(对).
题型探究
(2)如图是一个正方体的展开图,如果将它还原成正方体,那么AB,CD,EF,GH这四条线段所在的直线是异面直线的有几对?分别是哪几对?
解 三对,分别为AB与CD,AB与GH,EF与GH.
还原的正方体如图所示.
题型探究
判定异面直线的方法
(1)定义法:利用异面直线的定义,说明两条直线不平行,也不相交,即不可能同在一个平面内.
(2)利用异面直线的判定定理.
(3)反证法:假设两条直线不是异面直线,根据空间两条直线的位置关系,这两条直线一定共面,即可能相交或平行,然后推出矛盾即可.
反思感悟
四、异面直线所成的角
例4 如图,在正方体ABCD-EFGH中,O为侧面ADHE的中心,求:
(1)BE与CG所成的角的大小;
解 ∵CG∥FB,
∴∠EBF是异面直线BE与CG所成的角.
在Rt△EFB中,EF=FB,
∴BE与CG所成的角为45°.
∴∠EBF=45°,
题型探究
(2)FO与BD所成的角的大小.
题型探究
解 如图,连接FH,
∵FB∥AE,FB=AE,AE∥HD,AE=HD,
∴FB=HD,FB∥HD,
∴四边形FBDH是平行四边形,
∴BD∥FH,
∴∠HFO是FO与BD所成的角,
连接HA,AF,则△AFH是等边三角形,
又O是AH的中点,∴∠HFO=30°,
∴FO与BD所成的角为30°.
题型探究
延伸探究
在本例中,若P是平面EFGH的中心,其他条件不变,求OP和CD所成的角.
解 如图,连接EG,HF,
则P为HF的中点,
连接AF,AH,则OP∥AF,
又CD∥AB,
∴∠BAF(或其补角)为异面直线OP与CD所成的角,
∵△ABF是等腰直角三角形,∴∠BAF=45°,
∴OP与CD所成的角为45°.
题型探究
求异面直线所成的角的步骤
(1)找出(或作出)适合题设的角——用平移法,若题设中有中点,常考虑中位线;若异面直线依附于某几何体,且对异面直线平移有困难时,可利用该几何体的特殊点,将异面直线转化为相交直线.
(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的角.
(3)结论——设由(2)所求得的角的大小为θ.若0°<θ≤90°,则θ为所求;若90°<θ<180°,则180°-θ为所求.
反思感悟
3
检测反馈
PART THREE
1.若一个角的两边分别和另一个角的两边平行,那么这两个角
A.相等 B.互补
C.相等或互补 D.无法确定
√
解析 一个角的两边分别和另一个角的两边平行,那么这两个角相等或互补.
检测反馈
2.直线a与直线b相交,直线c也与直线b相交,则直线a与直线c的位置关系是
A.相交 B.平行 C.异面 D.以上都有可能
√
解析 如图所示,长方体ABCD-A1B1C1D1中,AB与AA1相交,A1B1与AA1相交,AB∥A1B1;
AD与AA1相交,AB与AD相交,AA1与AB相交;
A1D1与AA1相交,AB与AA1相交,AB与A1D1异面.
检测反馈
3.(多选)如图所示,G,H,M,N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有
√
√
检测反馈
解析 A中,直线GH∥MN;
B中,G,H,N三点共面,但M 平面GHN,且N GH,
因此直线GH与MN异面;
C中,连接MG(图略),GM∥HN,
因此,GH与MN共面;
D中,G,M,N三点共面,但H 平面GMN,且G MN,
所以GH与MN异面.
检测反馈
4.如图,在正方体ABCD-A′B′C′D′中,异面直线A′B′与BC所成的角的大小为________.异面直线AD′与BC所成的角的大小为________.
90°
45°
解析 ∵BC∥B′C′,∴∠A′B′C′即异面直线A′B′与BC所成的角,且∠A′B′C′=90°,又BC∥AD,
∴∠D′AD是异面直线AD′与BC所成的角,且∠D′AD=45°.
检测反馈
5.如图,在三棱锥A-BCD中,E,F,G分别是AB,BC,AD的中点,∠GEF=120°,则BD与AC所成的角的大小为________.
60°
解析 依题意知,EG∥BD,EF∥AC,
所以∠GEF(或其补角)即为异面直线AC与BD所成的角,
又∠GEF=120°,
所以异面直线BD与AC所成的角为60°.
检测反馈
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
