苏教版(2019)高中数学必修第二册 13.2.3直线与平面的位置关系—直线与平面平行的判定与性质练习(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 13.2.3直线与平面的位置关系—直线与平面平行的判定与性质练习(解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 431.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 17:01:29 | ||
图片预览




文档简介
13.2.3 直线与平面的位置关系—直线与平面平行的判定与性质
1.下列条件中能得出直线m与平面α平行的是( )
A.直线m与平面α内所有直线平行
B.直线m与平面α内无数条直线平行
C.直线m与平面α没有公共点
D.直线m与平面α内的一条直线平行
2.直线a,b为异面直线,过直线a与直线b平行的平面( )
A.有且只有一个
B.有无数多个
C.有且只有一个或不存在
D.不存在
3.如图所示,在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是( )
A.DD1 B.A1D1
C.C1D1 D.A1D
4.如图所示,已知S为四边形ABCD所在平面外一点,G,H分别为SB,BD上的点,若GH∥平面SCD,则( )
A.GH∥SA B.GH∥SD
C.GH∥SC D.以上均有可能
5.(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点.则下列结论成立的是( )
A.OM∥平面PCD B.OM∥平面PDA
C.OM∥平面PBA D.OM∥平面PBC
6.如图,在五面体FE-ABCD中,四边形CDEF为矩形,M,N分别是BF,BC的中点,则MN与平面ADE的位置关系是________.
7.在三棱锥SABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的位置关系为________.
8.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
9.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.求证:EF∥平面BDD1B1.
10.如图,四边形ABCD是矩形,P 平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.
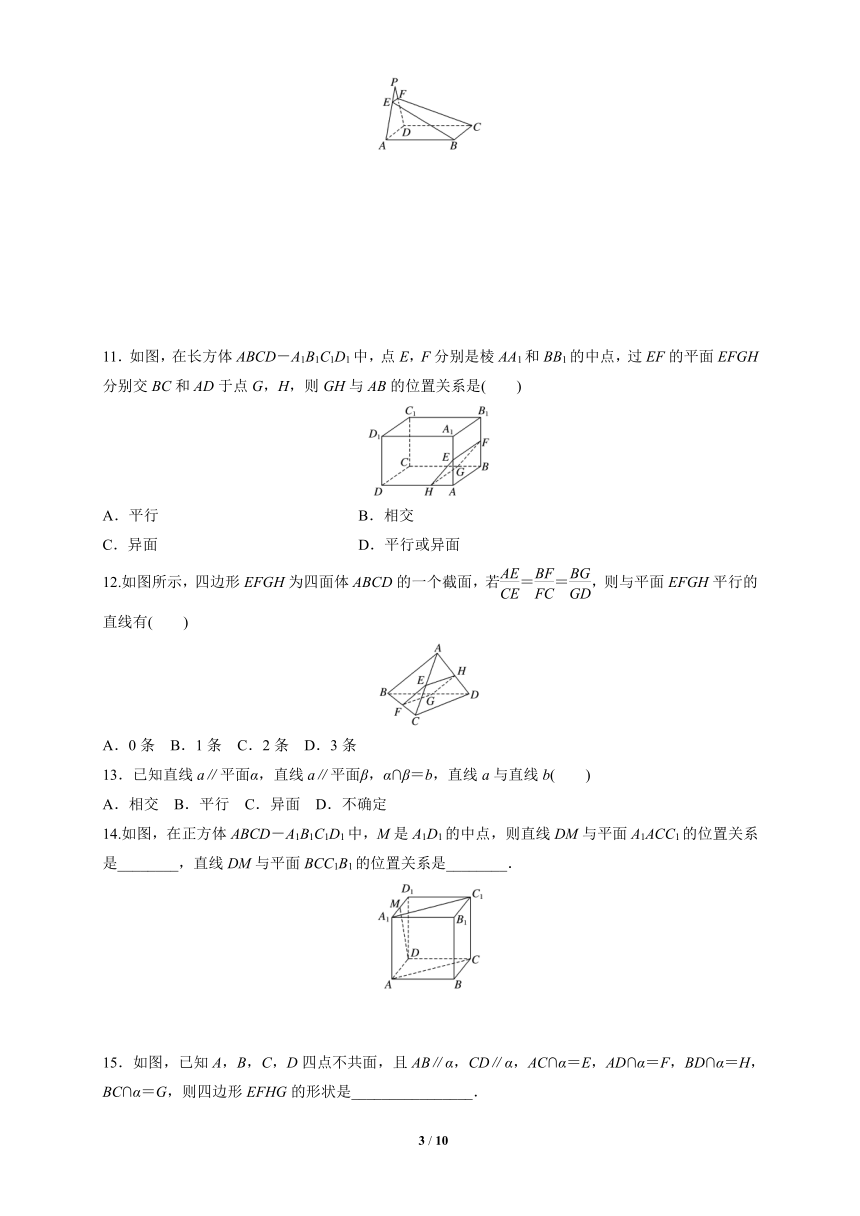
11.如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行 B.相交
C.异面 D.平行或异面
12.如图所示,四边形EFGH为四面体ABCD的一个截面,若==,则与平面EFGH平行的直线有( )
A.0条 B.1条 C.2条 D.3条
13.已知直线a∥平面α,直线a∥平面β,α∩β=b,直线a与直线b( )
A.相交 B.平行 C.异面 D.不确定
14.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线DM与平面A1ACC1的位置关系是________,直线DM与平面BCC1B1的位置关系是________.
15.如图,已知A,B,C,D四点不共面,且AB∥α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG的形状是________________.
16.如图,E为平行四边形ABCD所在平面外一点,P是线段CD的中点,在直线AE上是否存在一点M,使得PM∥平面BCE.若存在,指出点M的位置,并证明你的结论.
13.2.3 直线与平面的位置关系—直线与平面平行的判定与性质
1.下列条件中能得出直线m与平面α平行的是( )
A.直线m与平面α内所有直线平行
B.直线m与平面α内无数条直线平行
C.直线m与平面α没有公共点
D.直线m与平面α内的一条直线平行
【答案】 C
【解析】 对于A,本身说法错误;对于B,当直线m在平面α内时,m与α不平行;对于C,能推出m与α平行;对于D,当直线m在平面α内时,m与α不平行.
2.直线a,b为异面直线,过直线a与直线b平行的平面( )
A.有且只有一个
B.有无数多个
C.有且只有一个或不存在
D.不存在
【答案】 A
【解析】 在a上任取一点A,则过A与b平行的直线有且只有一条,设为b′,又∵a∩b′=A,∴a与b′确定一个平面α,即为过a与b平行的平面,可知它是唯一的.
3.如图所示,在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是( )
A.DD1 B.A1D1
C.C1D1 D.A1D
【答案】 D
【解析】 ∵A1B1綊AB綊CD,∴A1B1綊CD,
∴四边形A1B1CD为平行四边形,
∴A1D∥B1C,
又B1C 平面AB1C,A1D 平面AB1C,
∴A1D∥平面AB1C.
4.如图所示,已知S为四边形ABCD所在平面外一点,G,H分别为SB,BD上的点,若GH∥平面SCD,则( )
A.GH∥SA B.GH∥SD
C.GH∥SC D.以上均有可能
【答案】 B
【解析】 ∵GH∥平面SCD,GH 平面SBD,
平面SBD∩平面SCD=SD,
∴GH∥SD.
5.(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点.则下列结论成立的是( )
A.OM∥平面PCD B.OM∥平面PDA
C.OM∥平面PBA D.OM∥平面PBC
【答案】 AB
【解析】 矩形ABCD的对角线AC与BD交于点O,所以点O为BD的中点,在△PBD中,因为点M是PB的中点,所以OM是△PBD的中位线,OM∥PD,所以OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA,平面PBC相交.
6.如图,在五面体FE-ABCD中,四边形CDEF为矩形,M,N分别是BF,BC的中点,则MN与平面ADE的位置关系是________.
【答案】 平行
【解析】 ∵M,N分别是BF,BC的中点,
∴MN∥CF,
又四边形CDEF为矩形,
∴CF∥DE,∴MN∥DE.
又MN 平面ADE,DE 平面ADE,
∴MN∥平面ADE.
7.在三棱锥SABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的位置关系为________.
【答案】 平行
【解析】 如图,延长AG交BC于F,连接SF,则由G为△ABC的重心知AG∶GF=2∶1,
又AE∶ES=2∶1,∴EG∥SF,
又SF 平面SBC,EG 平面SBC,
∴EG∥平面SBC.
8.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
【答案】
【解析】 ∵MN∥平面AC,平面PMNQ∩平面AC=PQ,
MN 平面PQNM,
∴MN∥PQ,易知DP=DQ=,
故PQ==DP=.
9.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.求证:EF∥平面BDD1B1.
证明 取D1B1的中点O,连接OF,OB(图略).
∵F为C1D1的中点,
∴OF∥B1C1且OF=B1C1,
又BE∥B1C1,BE=B1C1,∴OF∥BE且OF=BE,
∴四边形OFEB是平行四边形,∴EF∥BO.
∵EF 平面BDD1B1,BO 平面BDD1B1,
∴EF∥平面BDD1B1.
10.如图,四边形ABCD是矩形,P 平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.
证明 ∵四边形ABCD为矩形,∴BC∥AD.
∵AD 平面PAD,BC 平面PAD,
∴BC∥平面PAD.
∵平面BCFE∩平面PAD=EF,BC 平面BCFE,
∴BC∥EF.
∵AD=BC,AD≠EF,∴BC≠EF,
∴四边形BCFE是梯形.
11.如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行 B.相交
C.异面 D.平行或异面
【答案】 A
【解析】 由长方体的性质知,EF∥平面ABCD,
∵EF 平面EFGH,平面EFGH∩平面ABCD=GH,
∴EF∥GH.
又EF∥AB,∴GH∥AB.
12.如图所示,四边形EFGH为四面体ABCD的一个截面,若==,则与平面EFGH平行的直线有( )
A.0条 B.1条 C.2条 D.3条
【答案】 C
【解析】 ∵=,∴EF∥AB.
又EF 平面EFGH,AB 平面EFGH,
∴AB∥平面EFGH.
同理,由=,
可证CD∥平面EFGH.
∴与平面EFGH平行的直线有2条.
13.已知直线a∥平面α,直线a∥平面β,α∩β=b,直线a与直线b( )
A.相交 B.平行 C.异面 D.不确定
【答案】 B
【解析】 因为直线a∥平面α,直线a∥平面β,
所以在α,β中均可找到一条直线与直线a平行.
设m在平面α内,n在平面β内,且m∥a,n∥a,
所以m∥n.
又因为m不在平面β内,n在平面β内,所以m∥β.
又因为α∩β=b,m α,所以m∥b.
又因为m∥a,所以a∥b,故选B.
14.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线DM与平面A1ACC1的位置关系是________,直线DM与平面BCC1B1的位置关系是________.
【答案】 相交 平行
【解析】 ∵M是A1D1的中点,
∴直线DM与直线AA1相交,
∴DM与平面A1ACC1有一个公共点,
∴DM与平面A1ACC1相交.
取B1C1的中点M1,连接MM1,M1C(图略).
∵MM1∥C1D1,C1D1∥CD,
∴MM1∥CD.
∵MM1=C1D1,C1D1=CD,
∴MM1=CD.
∴四边形DMM1C为平行四边形,
∴DM∥CM1,
又DM 平面BCC1B1,CM1 平面BCC1B1,
∴DM∥平面BCC1B1.
15.如图,已知A,B,C,D四点不共面,且AB∥α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG的形状是________________.
【答案】 平行四边形
【解析】 ∵AB∥α,平面ABC∩α=EG,AB 平面ABC,
∴EG∥AB.
同理FH∥AB,∴EG∥FH.
又CD∥α,平面BCD∩α=GH,CD 平面BCD,
∴GH∥CD.同理EF∥CD,
∴GH∥EF,∴四边形EFHG是平行四边形.
16.如图,E为平行四边形ABCD所在平面外一点,P是线段CD的中点,在直线AE上是否存在一点M,使得PM∥平面BCE.若存在,指出点M的位置,并证明你的结论.
解 存在点M,如图,当点M是线段AE的中点时,
PM∥平面BCE.
证明如下:取BE的中点N,连接CN,MN,
则MN∥AB且MN=AB,
又PC∥AB且PC=AB,所以MN∥PC且MN=PC,
所以四边形MNCP为平行四边形,所以PM∥CN.
因为PM 平面BCE,CN 平面BCE,
所以PM∥平面BCE.
2 / 10
1.下列条件中能得出直线m与平面α平行的是( )
A.直线m与平面α内所有直线平行
B.直线m与平面α内无数条直线平行
C.直线m与平面α没有公共点
D.直线m与平面α内的一条直线平行
2.直线a,b为异面直线,过直线a与直线b平行的平面( )
A.有且只有一个
B.有无数多个
C.有且只有一个或不存在
D.不存在
3.如图所示,在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是( )
A.DD1 B.A1D1
C.C1D1 D.A1D
4.如图所示,已知S为四边形ABCD所在平面外一点,G,H分别为SB,BD上的点,若GH∥平面SCD,则( )
A.GH∥SA B.GH∥SD
C.GH∥SC D.以上均有可能
5.(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点.则下列结论成立的是( )
A.OM∥平面PCD B.OM∥平面PDA
C.OM∥平面PBA D.OM∥平面PBC
6.如图,在五面体FE-ABCD中,四边形CDEF为矩形,M,N分别是BF,BC的中点,则MN与平面ADE的位置关系是________.
7.在三棱锥SABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的位置关系为________.
8.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
9.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.求证:EF∥平面BDD1B1.
10.如图,四边形ABCD是矩形,P 平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.
11.如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行 B.相交
C.异面 D.平行或异面
12.如图所示,四边形EFGH为四面体ABCD的一个截面,若==,则与平面EFGH平行的直线有( )
A.0条 B.1条 C.2条 D.3条
13.已知直线a∥平面α,直线a∥平面β,α∩β=b,直线a与直线b( )
A.相交 B.平行 C.异面 D.不确定
14.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线DM与平面A1ACC1的位置关系是________,直线DM与平面BCC1B1的位置关系是________.
15.如图,已知A,B,C,D四点不共面,且AB∥α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG的形状是________________.
16.如图,E为平行四边形ABCD所在平面外一点,P是线段CD的中点,在直线AE上是否存在一点M,使得PM∥平面BCE.若存在,指出点M的位置,并证明你的结论.
13.2.3 直线与平面的位置关系—直线与平面平行的判定与性质
1.下列条件中能得出直线m与平面α平行的是( )
A.直线m与平面α内所有直线平行
B.直线m与平面α内无数条直线平行
C.直线m与平面α没有公共点
D.直线m与平面α内的一条直线平行
【答案】 C
【解析】 对于A,本身说法错误;对于B,当直线m在平面α内时,m与α不平行;对于C,能推出m与α平行;对于D,当直线m在平面α内时,m与α不平行.
2.直线a,b为异面直线,过直线a与直线b平行的平面( )
A.有且只有一个
B.有无数多个
C.有且只有一个或不存在
D.不存在
【答案】 A
【解析】 在a上任取一点A,则过A与b平行的直线有且只有一条,设为b′,又∵a∩b′=A,∴a与b′确定一个平面α,即为过a与b平行的平面,可知它是唯一的.
3.如图所示,在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是( )
A.DD1 B.A1D1
C.C1D1 D.A1D
【答案】 D
【解析】 ∵A1B1綊AB綊CD,∴A1B1綊CD,
∴四边形A1B1CD为平行四边形,
∴A1D∥B1C,
又B1C 平面AB1C,A1D 平面AB1C,
∴A1D∥平面AB1C.
4.如图所示,已知S为四边形ABCD所在平面外一点,G,H分别为SB,BD上的点,若GH∥平面SCD,则( )
A.GH∥SA B.GH∥SD
C.GH∥SC D.以上均有可能
【答案】 B
【解析】 ∵GH∥平面SCD,GH 平面SBD,
平面SBD∩平面SCD=SD,
∴GH∥SD.
5.(多选)如图,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点.则下列结论成立的是( )
A.OM∥平面PCD B.OM∥平面PDA
C.OM∥平面PBA D.OM∥平面PBC
【答案】 AB
【解析】 矩形ABCD的对角线AC与BD交于点O,所以点O为BD的中点,在△PBD中,因为点M是PB的中点,所以OM是△PBD的中位线,OM∥PD,所以OM∥平面PCD,且OM∥平面PDA.因为M∈PB,所以OM与平面PBA,平面PBC相交.
6.如图,在五面体FE-ABCD中,四边形CDEF为矩形,M,N分别是BF,BC的中点,则MN与平面ADE的位置关系是________.
【答案】 平行
【解析】 ∵M,N分别是BF,BC的中点,
∴MN∥CF,
又四边形CDEF为矩形,
∴CF∥DE,∴MN∥DE.
又MN 平面ADE,DE 平面ADE,
∴MN∥平面ADE.
7.在三棱锥SABC中,G为△ABC的重心,E在棱SA上,且AE=2ES,则EG与平面SBC的位置关系为________.
【答案】 平行
【解析】 如图,延长AG交BC于F,连接SF,则由G为△ABC的重心知AG∶GF=2∶1,
又AE∶ES=2∶1,∴EG∥SF,
又SF 平面SBC,EG 平面SBC,
∴EG∥平面SBC.
8.如图所示,ABCD—A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=________.
【答案】
【解析】 ∵MN∥平面AC,平面PMNQ∩平面AC=PQ,
MN 平面PQNM,
∴MN∥PQ,易知DP=DQ=,
故PQ==DP=.
9.如图所示,在正方体ABCD-A1B1C1D1中,E,F分别是棱BC,C1D1的中点.求证:EF∥平面BDD1B1.
证明 取D1B1的中点O,连接OF,OB(图略).
∵F为C1D1的中点,
∴OF∥B1C1且OF=B1C1,
又BE∥B1C1,BE=B1C1,∴OF∥BE且OF=BE,
∴四边形OFEB是平行四边形,∴EF∥BO.
∵EF 平面BDD1B1,BO 平面BDD1B1,
∴EF∥平面BDD1B1.
10.如图,四边形ABCD是矩形,P 平面ABCD,过BC作平面BCFE交AP于点E,交DP于点F,求证:四边形BCFE是梯形.
证明 ∵四边形ABCD为矩形,∴BC∥AD.
∵AD 平面PAD,BC 平面PAD,
∴BC∥平面PAD.
∵平面BCFE∩平面PAD=EF,BC 平面BCFE,
∴BC∥EF.
∵AD=BC,AD≠EF,∴BC≠EF,
∴四边形BCFE是梯形.
11.如图,在长方体ABCD-A1B1C1D1中,点E,F分别是棱AA1和BB1的中点,过EF的平面EFGH分别交BC和AD于点G,H,则GH与AB的位置关系是( )
A.平行 B.相交
C.异面 D.平行或异面
【答案】 A
【解析】 由长方体的性质知,EF∥平面ABCD,
∵EF 平面EFGH,平面EFGH∩平面ABCD=GH,
∴EF∥GH.
又EF∥AB,∴GH∥AB.
12.如图所示,四边形EFGH为四面体ABCD的一个截面,若==,则与平面EFGH平行的直线有( )
A.0条 B.1条 C.2条 D.3条
【答案】 C
【解析】 ∵=,∴EF∥AB.
又EF 平面EFGH,AB 平面EFGH,
∴AB∥平面EFGH.
同理,由=,
可证CD∥平面EFGH.
∴与平面EFGH平行的直线有2条.
13.已知直线a∥平面α,直线a∥平面β,α∩β=b,直线a与直线b( )
A.相交 B.平行 C.异面 D.不确定
【答案】 B
【解析】 因为直线a∥平面α,直线a∥平面β,
所以在α,β中均可找到一条直线与直线a平行.
设m在平面α内,n在平面β内,且m∥a,n∥a,
所以m∥n.
又因为m不在平面β内,n在平面β内,所以m∥β.
又因为α∩β=b,m α,所以m∥b.
又因为m∥a,所以a∥b,故选B.
14.如图,在正方体ABCD-A1B1C1D1中,M是A1D1的中点,则直线DM与平面A1ACC1的位置关系是________,直线DM与平面BCC1B1的位置关系是________.
【答案】 相交 平行
【解析】 ∵M是A1D1的中点,
∴直线DM与直线AA1相交,
∴DM与平面A1ACC1有一个公共点,
∴DM与平面A1ACC1相交.
取B1C1的中点M1,连接MM1,M1C(图略).
∵MM1∥C1D1,C1D1∥CD,
∴MM1∥CD.
∵MM1=C1D1,C1D1=CD,
∴MM1=CD.
∴四边形DMM1C为平行四边形,
∴DM∥CM1,
又DM 平面BCC1B1,CM1 平面BCC1B1,
∴DM∥平面BCC1B1.
15.如图,已知A,B,C,D四点不共面,且AB∥α,CD∥α,AC∩α=E,AD∩α=F,BD∩α=H,BC∩α=G,则四边形EFHG的形状是________________.
【答案】 平行四边形
【解析】 ∵AB∥α,平面ABC∩α=EG,AB 平面ABC,
∴EG∥AB.
同理FH∥AB,∴EG∥FH.
又CD∥α,平面BCD∩α=GH,CD 平面BCD,
∴GH∥CD.同理EF∥CD,
∴GH∥EF,∴四边形EFHG是平行四边形.
16.如图,E为平行四边形ABCD所在平面外一点,P是线段CD的中点,在直线AE上是否存在一点M,使得PM∥平面BCE.若存在,指出点M的位置,并证明你的结论.
解 存在点M,如图,当点M是线段AE的中点时,
PM∥平面BCE.
证明如下:取BE的中点N,连接CN,MN,
则MN∥AB且MN=AB,
又PC∥AB且PC=AB,所以MN∥PC且MN=PC,
所以四边形MNCP为平行四边形,所以PM∥CN.
因为PM 平面BCE,CN 平面BCE,
所以PM∥平面BCE.
2 / 10
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
