《几何概型》课件
图片预览




文档简介
课件18张PPT。3.3.1 几何概型古典概型的两个基本特征?有限性:在一次试验中,可能出现的结果只有有限个,即只有有限个不同的基本事件;
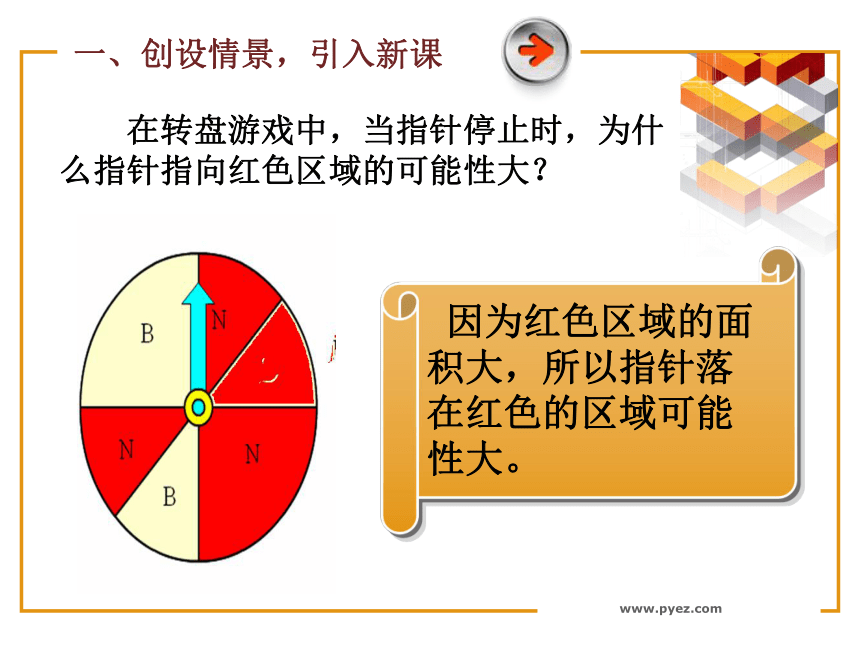
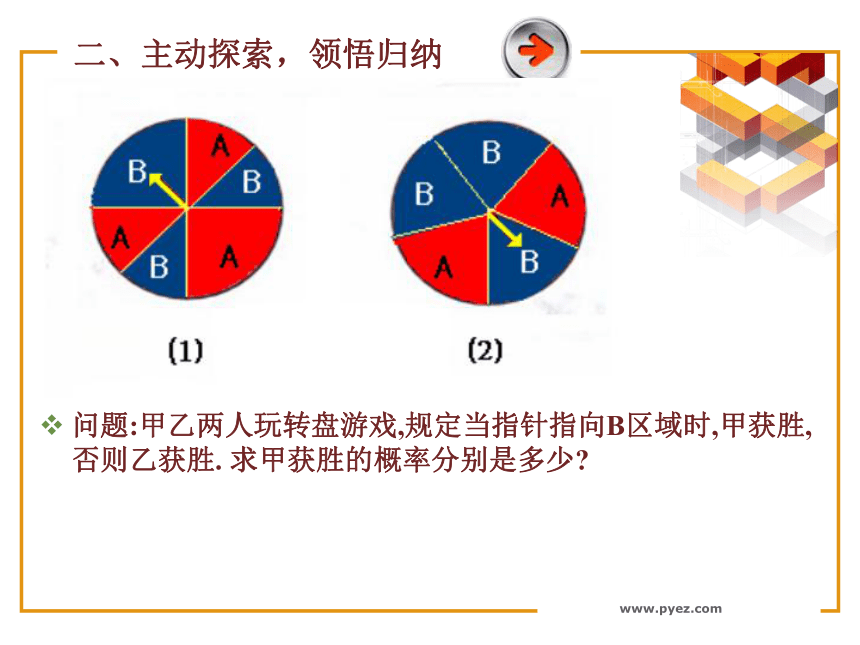
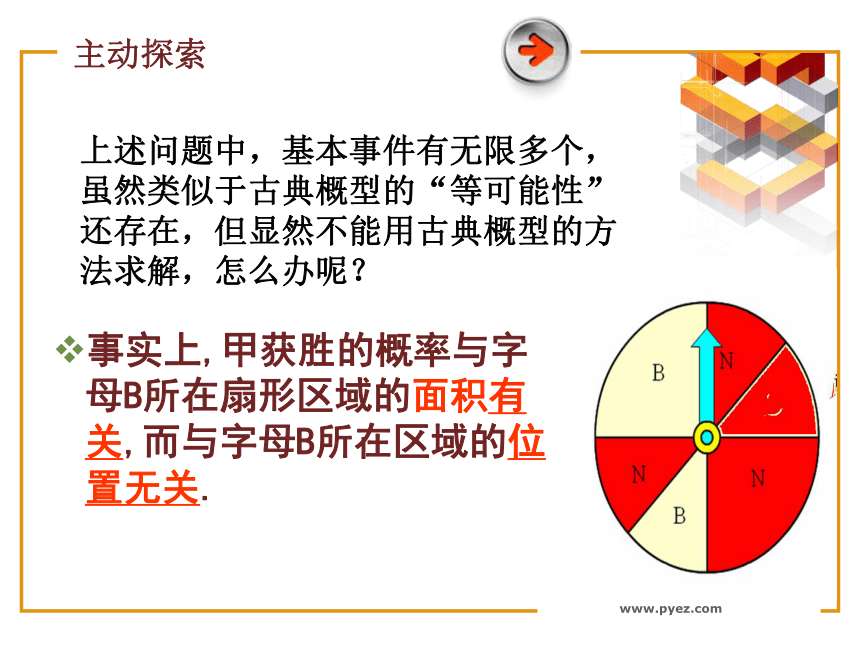
等可能性:每个基本事件发生的可能性是相等的.现实生活中,有没有实验的所有可能结果是无穷多的情况?相应的概率如何求?复习回顾www.pyez.com 在转盘游戏中,当指针停止时,为什么指针指向红色区域的可能性大? 因为红色区域的面积大,所以指针落在红色的区域可能性大。一、创设情景,引入新课www.pyez.com问题:甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜. 求甲获胜的概率分别是多少?二、主动探索,领悟归纳www.pyez.com事实上,甲获胜的概率与字母B所在扇形区域的面积有关,而与字母B所在区域的位置无关.上述问题中,基本事件有无限多个,虽然类似于古典概型的“等可能性”还存在,但显然不能用古典概型的方法求解,怎么办呢?主动探索www.pyez.com 对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中的每一个点被取到的机会都一样,而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点.这里的区域可以是线段、平面图形、立体图形等.形成概念www.pyez.com如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.领悟归纳几何概型的特点:(1)基本事件有无限多个;(2)基本事件发生是等可能的.www.pyez.com 一般地,在几何区域D中随机地取一点,记“该点落在其内部一个区域d内”为事件A,则事件A发生的概率:即:www.pyez.com注:(2)D的测度不为0,当D分别是线段、平面图形、立体图形时,相应的“测度”分别是长度、面积和体积.(1)古典概型与几何概型的区别在于:
几何概型是无限多个等可能事件的情况,而古典概型中的等可能事件只有有限多个;www.pyez.com例1 某人午觉醒来,发现表停了,他
打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.分析:假设他在0-60分钟之间任何一个时刻打开收音机是等可能的,但0-60之间有无穷个时刻,不能用古典概型的公式计算随机事件发生的概率。可以通过几何概型的求概率公式得到事件发生的概率。 三、巩固深化,应用拓展几何概型的计算www.pyez.com例2.有一杯500ml的水,其中含有1个细菌,用一个小杯从这杯水中取出2ml升,求小杯水中含有这个细菌的概率.例3.如右图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到红色部分的概率.www.pyez.com对于复杂的实际问题,解题的关键是要建立模型,找出随机事件与所有基本事件相对应的几何区域,把问题转化为几何概率问题,利用几何概率公式求解.学法领悟www.pyez.com1.公共汽车在0~5分钟内随机地到达车站,求汽车在1~3分钟之间到达的概率。分析:将0~5分钟这段时间看作是一段长度为5
个单位长度的线段,则1~3分钟是这一线段中
的2个单位长度。解:设“汽车在1~3分钟之间到达”为事件A,则所以“汽车在1~3分钟之间到达”的概率为练习www.pyez.com(1)豆子落在红色区域;
(2)豆子落在黄色区域;
(3)豆子落在绿色区域;
(4)豆子落在红色或绿色区域;
(5)豆子落在黄色或绿色区域。2.一张方桌的图案如图所示。将一颗豆子随机地扔到桌面上,假设豆子不落在线上,求下列事件的概率:www.pyez.com3.取一根长为3米的绳子,拉直后在任意位置剪断,那么剪得两段的长都不少于1米的概率有多大?解:如上图,记“剪得两段绳子长都不小于1m”为事件A,把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生。由于中间一段的长度等于绳子长的三分之一,所以事件A发生的概率P(A)=1/3。3m1m1m练习www.pyez.com4.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率。分析:点M随机地落在线段AB上,故线段AB为区域D。当点M位于图中的线段AC’上时,AM<AC,故线段AC’即为区域d。解: 在AB上截取AC’=AC,于是
P(AM<AC)=P(AM<AC’)则AM小于AC的概率为练习www.pyez.com5.在半径为1的圆上随机地取两点,连成一条线,则其长超过圆内等边三角形的边长的概率是多少?BCDE.0解:记事件A={弦长超过圆内接
等边三角形的边长},取圆内接
等边三角形BCD的顶点B为弦
的一个端点,当另一点在劣弧
CD上时,|BE|>|BC|,而弧CD
的长度是圆周长的三分之一,
所以可用几何概型求解,有
则“弦长超过圆内接等边三角形的边长”的概率为练习www.pyez.com1.几何概型的特点.
2.古典概型与几何概型的区别:
1)两种模型的基本事件发生的可能性都相等;
2)古典概型要求基本事件是有限个,而几何概型则要求基本事件有无限多个。
3.几何概型的概率公式及运用.
四、总结评价,促进成长www.pyez.com
等可能性:每个基本事件发生的可能性是相等的.现实生活中,有没有实验的所有可能结果是无穷多的情况?相应的概率如何求?复习回顾www.pyez.com 在转盘游戏中,当指针停止时,为什么指针指向红色区域的可能性大? 因为红色区域的面积大,所以指针落在红色的区域可能性大。一、创设情景,引入新课www.pyez.com问题:甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜. 求甲获胜的概率分别是多少?二、主动探索,领悟归纳www.pyez.com事实上,甲获胜的概率与字母B所在扇形区域的面积有关,而与字母B所在区域的位置无关.上述问题中,基本事件有无限多个,虽然类似于古典概型的“等可能性”还存在,但显然不能用古典概型的方法求解,怎么办呢?主动探索www.pyez.com 对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,该区域中的每一个点被取到的机会都一样,而一个随机事件的发生则理解为恰好取到上述区域内的某个指定区域中的点.这里的区域可以是线段、平面图形、立体图形等.形成概念www.pyez.com如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.领悟归纳几何概型的特点:(1)基本事件有无限多个;(2)基本事件发生是等可能的.www.pyez.com 一般地,在几何区域D中随机地取一点,记“该点落在其内部一个区域d内”为事件A,则事件A发生的概率:即:www.pyez.com注:(2)D的测度不为0,当D分别是线段、平面图形、立体图形时,相应的“测度”分别是长度、面积和体积.(1)古典概型与几何概型的区别在于:
几何概型是无限多个等可能事件的情况,而古典概型中的等可能事件只有有限多个;www.pyez.com例1 某人午觉醒来,发现表停了,他
打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.分析:假设他在0-60分钟之间任何一个时刻打开收音机是等可能的,但0-60之间有无穷个时刻,不能用古典概型的公式计算随机事件发生的概率。可以通过几何概型的求概率公式得到事件发生的概率。 三、巩固深化,应用拓展几何概型的计算www.pyez.com例2.有一杯500ml的水,其中含有1个细菌,用一个小杯从这杯水中取出2ml升,求小杯水中含有这个细菌的概率.例3.如右图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到红色部分的概率.www.pyez.com对于复杂的实际问题,解题的关键是要建立模型,找出随机事件与所有基本事件相对应的几何区域,把问题转化为几何概率问题,利用几何概率公式求解.学法领悟www.pyez.com1.公共汽车在0~5分钟内随机地到达车站,求汽车在1~3分钟之间到达的概率。分析:将0~5分钟这段时间看作是一段长度为5
个单位长度的线段,则1~3分钟是这一线段中
的2个单位长度。解:设“汽车在1~3分钟之间到达”为事件A,则所以“汽车在1~3分钟之间到达”的概率为练习www.pyez.com(1)豆子落在红色区域;
(2)豆子落在黄色区域;
(3)豆子落在绿色区域;
(4)豆子落在红色或绿色区域;
(5)豆子落在黄色或绿色区域。2.一张方桌的图案如图所示。将一颗豆子随机地扔到桌面上,假设豆子不落在线上,求下列事件的概率:www.pyez.com3.取一根长为3米的绳子,拉直后在任意位置剪断,那么剪得两段的长都不少于1米的概率有多大?解:如上图,记“剪得两段绳子长都不小于1m”为事件A,把绳子三等分,于是当剪断位置处在中间一段上时,事件A发生。由于中间一段的长度等于绳子长的三分之一,所以事件A发生的概率P(A)=1/3。3m1m1m练习www.pyez.com4.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率。分析:点M随机地落在线段AB上,故线段AB为区域D。当点M位于图中的线段AC’上时,AM<AC,故线段AC’即为区域d。解: 在AB上截取AC’=AC,于是
P(AM<AC)=P(AM<AC’)则AM小于AC的概率为练习www.pyez.com5.在半径为1的圆上随机地取两点,连成一条线,则其长超过圆内等边三角形的边长的概率是多少?BCDE.0解:记事件A={弦长超过圆内接
等边三角形的边长},取圆内接
等边三角形BCD的顶点B为弦
的一个端点,当另一点在劣弧
CD上时,|BE|>|BC|,而弧CD
的长度是圆周长的三分之一,
所以可用几何概型求解,有
则“弦长超过圆内接等边三角形的边长”的概率为练习www.pyez.com1.几何概型的特点.
2.古典概型与几何概型的区别:
1)两种模型的基本事件发生的可能性都相等;
2)古典概型要求基本事件是有限个,而几何概型则要求基本事件有无限多个。
3.几何概型的概率公式及运用.
四、总结评价,促进成长www.pyez.com
