教科版九年级物理上册5.3 等效电路 课件(共23张PPT)
文档属性
| 名称 | 教科版九年级物理上册5.3 等效电路 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-12-15 23:03:53 | ||
图片预览







文档简介
(共23张PPT)
欧姆定律的应用之二
5.3 等效电路
导入:在维修爷爷的收音机时,小聪发现收音机中有一只100Ω的电阻坏了,可小聪手边只有几只50Ω的定值电阻,有什么办法可以解决这个问题?
100Ω的电阻坏了,怎样用50Ω的电阻替代?
几个连接起来的电阻所起的作用,可以用一个电阻来代替,这个电阻就是那些电阻的等效电阻。
我们可以用伏安法做实验来探究。
两只50Ω的定值电阻串联,是不是可以替代100Ω的电阻?
我想,从理论上也也应该能推导出来吧!
电路图
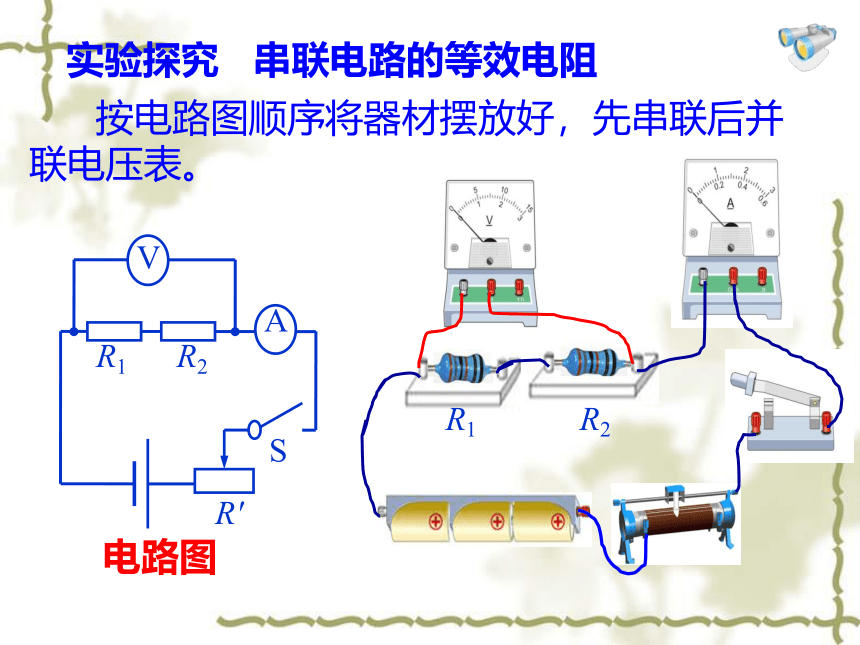
实验探究 串联电路的等效电阻
按电路图顺序将器材摆放好,先串联后并联电压表。
R1
R2
R1
R2
S
R'
A
V
实验探究 串联电路的等效电阻
将R的值与R1、R2的值比较,看有什么关系。
实验得出结论:串联电路的等效电阻等于各串联电阻之和
R=R1+R2
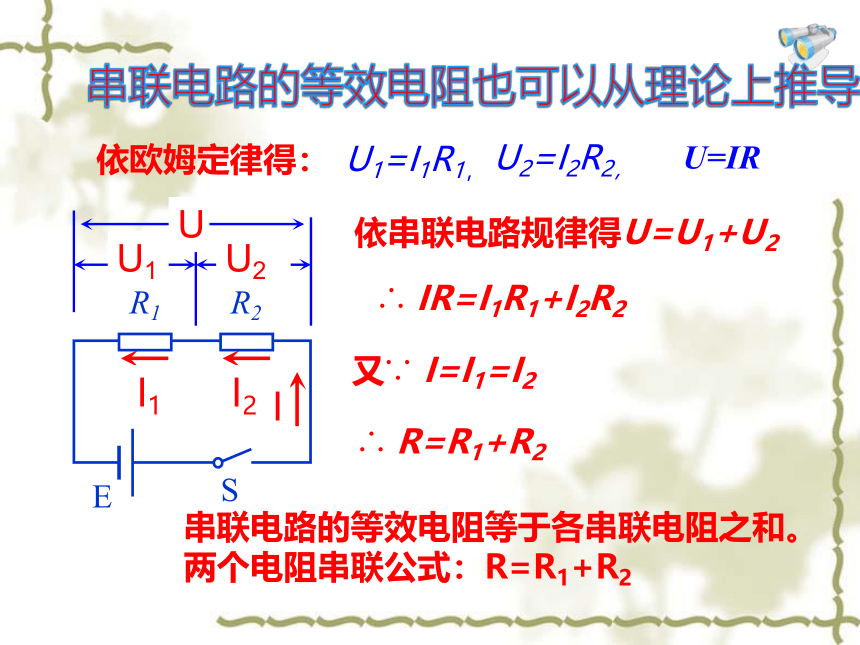
U1=I1R1,
依欧姆定律得:
U
U1
U2
I
I2
I1
R1
R2
S
E
U=IR
依串联电路规律得U=U1+U2
∴ IR=I1R1+I2R2
又∵ I=I1=I2
∴ R=R1+R2
串联电路的等效电阻等于各串联电阻之和。
两个电阻串联公式:R=R1+R2
U2=I2R2,
串联电路的等效电阻等于各串联电阻之和。R=R1+R2
串联导体相当于增加了导体的长度,所以等效电阻大于任何一个串联导体的电阻。
1. 一个5Ω的电阻和一个10Ω的电阻串联 ,等效电阻是( )
A.5Ω
B.10Ω
C.15Ω
D.20Ω
C
2. 一个10Ω的电阻和一个10Ω的电阻串联 ,等效电阻是( )
A.5Ω
B.10Ω
C.15Ω
D.20Ω
D
依欧姆定律得:
U1
U2
I
I2
I1
依并联电路规律得I=I1+I2
又∵ U=U1=U2
R1
R2
S
E
U
并联电路的等效电阻的倒数等于各支路电阻的倒数之和。
并联导体相当于增加了导体的 ,所以并联的等效电阻 于各并联导体的电阻。
横截面积
小
支路电阻的倒数之和。
并联电路的等效电阻的倒数等于各
3. 一个10Ω的电阻和一个10Ω的电阻并联 ,等效电阻是( )
A.5Ω
B.10Ω
C.15Ω
D.20Ω
A
R2、R3并联再和R1串联,先算并联,后算串联。
先算R2、R3的等效电阻R23,再算R1、R23的等效电阻R123。
S
R1
R2
R3
S
R1
R23
S
R123
我的收获
几个连接起来的电阻所起作用,可以用一个电阻来代替,这个电阻就是那些电阻的等效电阻。
串联电路的等效电阻等于各串联电阻之和。
两个电阻串联,有R=R1+R2。
并联电路的等效电阻的倒数等于各支路电阻的倒数之和。两个电阻并联,
串联电阻增长度,等效电阻大于分电阻。
并联电阻增面积,等效电阻小于分电阻。
4.有两个电阻,R1=3Ω, R2=9Ω,把它们串联后接到电路中,它们的总电阻是 ,通过它们的电流比I1 :I2 = ,它们两端的电压之比U1 :U2 = 。
12Ω
1:1
1:3
5. 要想得到一个20Ω的电阻,需要5Ω的电阻串联 个数是( )
A.5
B.4
C.3
D.20
B
5.两导体电阻R1=20Ω,R2=5Ω,串联起来,等效电阻R的阻值 ( )
A.10Ω
B.20Ω
C.25Ω
D.15Ω。
C
6.一个灯泡正常发光时电压为2.5V,电阻R1=10Ω,接6V的电源上,需要串联一个多大阻值的电阻才能正常发光 ( )
A.10Ω
B.15Ω
C.14Ω
D.12Ω。
C
7.电阻R1=3Ω,R2 =6Ω,电源电压为12V,求R1、R2 的电压.
解:
R等效
I
1
I
R
1
R
2
U=12V
8. 如图所示,已知I=4.5 A,I2=0.9 A,电源电压为36 V,那么灯L1的电阻R1多大?
解:∵ 灯L1和灯L2并联
∴ I = I1 + I2
I1 = I - I2 = 4.5 A -0.9 A = 3.6 A
而 U1 = U2 =U= 36 V
L2
I2
I
36 V
L1
I1
∴R1= = = 10 Ω
U1
I1
36 V
3.6 A
欧姆定律的应用之二
5.3 等效电路
导入:在维修爷爷的收音机时,小聪发现收音机中有一只100Ω的电阻坏了,可小聪手边只有几只50Ω的定值电阻,有什么办法可以解决这个问题?
100Ω的电阻坏了,怎样用50Ω的电阻替代?
几个连接起来的电阻所起的作用,可以用一个电阻来代替,这个电阻就是那些电阻的等效电阻。
我们可以用伏安法做实验来探究。
两只50Ω的定值电阻串联,是不是可以替代100Ω的电阻?
我想,从理论上也也应该能推导出来吧!
电路图
实验探究 串联电路的等效电阻
按电路图顺序将器材摆放好,先串联后并联电压表。
R1
R2
R1
R2
S
R'
A
V
实验探究 串联电路的等效电阻
将R的值与R1、R2的值比较,看有什么关系。
实验得出结论:串联电路的等效电阻等于各串联电阻之和
R=R1+R2
U1=I1R1,
依欧姆定律得:
U
U1
U2
I
I2
I1
R1
R2
S
E
U=IR
依串联电路规律得U=U1+U2
∴ IR=I1R1+I2R2
又∵ I=I1=I2
∴ R=R1+R2
串联电路的等效电阻等于各串联电阻之和。
两个电阻串联公式:R=R1+R2
U2=I2R2,
串联电路的等效电阻等于各串联电阻之和。R=R1+R2
串联导体相当于增加了导体的长度,所以等效电阻大于任何一个串联导体的电阻。
1. 一个5Ω的电阻和一个10Ω的电阻串联 ,等效电阻是( )
A.5Ω
B.10Ω
C.15Ω
D.20Ω
C
2. 一个10Ω的电阻和一个10Ω的电阻串联 ,等效电阻是( )
A.5Ω
B.10Ω
C.15Ω
D.20Ω
D
依欧姆定律得:
U1
U2
I
I2
I1
依并联电路规律得I=I1+I2
又∵ U=U1=U2
R1
R2
S
E
U
并联电路的等效电阻的倒数等于各支路电阻的倒数之和。
并联导体相当于增加了导体的 ,所以并联的等效电阻 于各并联导体的电阻。
横截面积
小
支路电阻的倒数之和。
并联电路的等效电阻的倒数等于各
3. 一个10Ω的电阻和一个10Ω的电阻并联 ,等效电阻是( )
A.5Ω
B.10Ω
C.15Ω
D.20Ω
A
R2、R3并联再和R1串联,先算并联,后算串联。
先算R2、R3的等效电阻R23,再算R1、R23的等效电阻R123。
S
R1
R2
R3
S
R1
R23
S
R123
我的收获
几个连接起来的电阻所起作用,可以用一个电阻来代替,这个电阻就是那些电阻的等效电阻。
串联电路的等效电阻等于各串联电阻之和。
两个电阻串联,有R=R1+R2。
并联电路的等效电阻的倒数等于各支路电阻的倒数之和。两个电阻并联,
串联电阻增长度,等效电阻大于分电阻。
并联电阻增面积,等效电阻小于分电阻。
4.有两个电阻,R1=3Ω, R2=9Ω,把它们串联后接到电路中,它们的总电阻是 ,通过它们的电流比I1 :I2 = ,它们两端的电压之比U1 :U2 = 。
12Ω
1:1
1:3
5. 要想得到一个20Ω的电阻,需要5Ω的电阻串联 个数是( )
A.5
B.4
C.3
D.20
B
5.两导体电阻R1=20Ω,R2=5Ω,串联起来,等效电阻R的阻值 ( )
A.10Ω
B.20Ω
C.25Ω
D.15Ω。
C
6.一个灯泡正常发光时电压为2.5V,电阻R1=10Ω,接6V的电源上,需要串联一个多大阻值的电阻才能正常发光 ( )
A.10Ω
B.15Ω
C.14Ω
D.12Ω。
C
7.电阻R1=3Ω,R2 =6Ω,电源电压为12V,求R1、R2 的电压.
解:
R等效
I
1
I
R
1
R
2
U=12V
8. 如图所示,已知I=4.5 A,I2=0.9 A,电源电压为36 V,那么灯L1的电阻R1多大?
解:∵ 灯L1和灯L2并联
∴ I = I1 + I2
I1 = I - I2 = 4.5 A -0.9 A = 3.6 A
而 U1 = U2 =U= 36 V
L2
I2
I
36 V
L1
I1
∴R1= = = 10 Ω
U1
I1
36 V
3.6 A
同课章节目录
