云南省2014年1月普通高中学业水平考试数学试卷(无答案)
文档属性
| 名称 | 云南省2014年1月普通高中学业水平考试数学试卷(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 68.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-13 09:06:08 | ||
图片预览

文档简介
【考试时间:2014年1月12日上午8:30——10:10,共100分钟】
云南省2014年1月普通高中学业水平考试
数学试卷
[考生注意]:必须在答题卡上指定位置按规定要求作答,答在试卷上一律无效.
参考公式:
如果事件A、B互斥,那么.
球的表面积公式:,体积公式:,其中R表示球的体积.
柱体的体积公式:,其中S表示柱体的底面面积,h表示柱体的高.
锥体的体积公式:,其中S表示锥体的底面面积,h表示锥体的高.
选择题(共51分)
一、选择题:本大题共17个小题,每小题3分,共51分。在每小题给出的四个选项中,只有一项符合题目要求,请在答题卡相应的位置上填涂。
1. 设集合,,则下列关系正确的是
A. B. C. D.
2. 有一个几何体的三视图如下图所示,这个几何体是一个
A.棱台
B.棱锥
C.棱柱
D.圆柱
3. 已知向量,,则等于
A.1 B. C.2 D.
4.如图是某运动员在某个赛季得分的茎叶统计图,则该运动员得分的中位数是
A.2 B.3
C.22 D.23
5.函数的零点时
A.0 B. C. D.
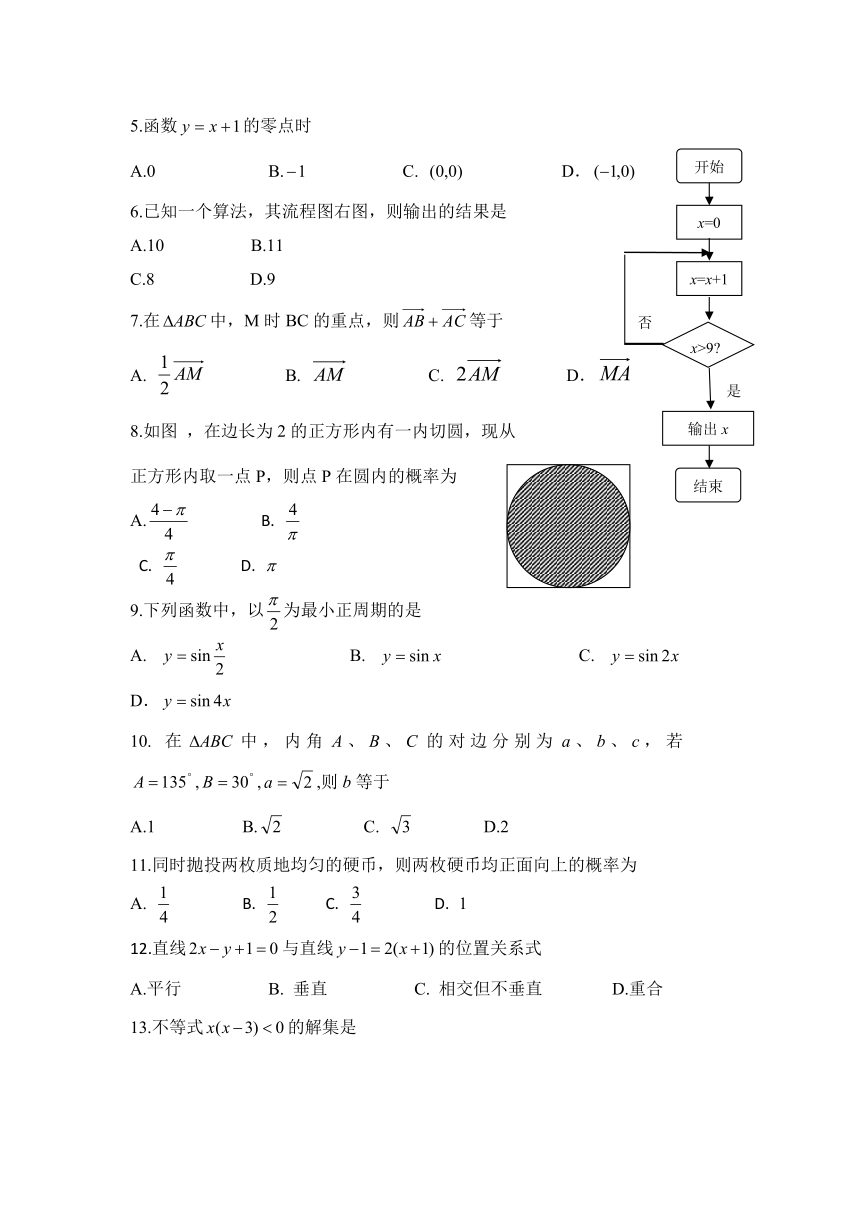
6.已知一个算法,其流程图右图,则输出的结果是
A.10 B.11
C.8 D.9
7.在中,M时BC的重点,则等于
A. B. C. D.
8.如图 ,在边长为2的正方形内有一内切圆,现从
正方形内取一点P,则点P在圆内的概率为
A. B.
C. D.
9.下列函数中,以为最小正周期的是
A. B. C. D.
10. 在中,内角A、B、C的对边分别为a、b、c,若,,,则b等于
A.1 B. C. D.2
11.同时抛投两枚质地均匀的硬币,则两枚硬币均正面向上的概率为
A. B. C. D.
12.直线与直线的位置关系式
A.平行 B. 垂直 C. 相交但不垂直 D.重合
13.不等式的解集是
A. B. C. D.
14.已知函数,用秦九昭算法计算的值时,首先计算的最内层括号内一次多项式的值是
A. 1 B. 2 C. 3 D. 4
15. 已知函数,则下列说话正确的是
A. 为奇函数,且在上是增函数
B. 为奇函数,且在上是减函数
C. 为偶函数,且在上是增函数
D. 为偶函数,且在上是偶函数
16. 已知数列是公比为实数的等比数列,且,,则等于
A2 B. 3 C. 4 D. 5
17.已知直线l过点,圆C:,则直线l与圆C的位置关系是
A.相交 B. 相切 C.相交和相切 D.相离
非选择题(共49分)
二、 填空题:本大题共5个小题,每小题3分,共15分。请把答案写在答题卡相应的位置上。
18.某工厂生产A、B、C三种不同型号的产品,产品数列之比一次为2:3:5,现用分层抽样的方法抽出一个容量为n的样本,其中A种型号产品有16件,那么此样本的容量n= .
19.直线的纵截距是 .
20.化简= .
21. 若实数x,y满足约束条件:,则的最大值等于 .
22.函数在区间上的最大值是 .
三、解答题:本大题共4小题,共34分.解答应写出文字说明、证明过程或演算步骤.
23. (本小题满分8分)已知.
(1)求的值及的最大值;
(2)求的递减区间
24. (本小题满分8分)
如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点。
(1)求证:;
(2)若,,求证:.
25. (本小题满分8分)
某商场的一种商品每件进价为10元,据调查知每日销售量m(件)与销售价x(元)之间的函数关系为,.设该商场日销售这种商品的利润为y(元).(单件利润=销售单价-进价;日销售利润=单件利润日销售量)
(1)求函数的解析式;
(2)求该商场销售这种商品的日销售利润的最大值.
26. (本小题满分10分)
已知正项数列的前n项和为,且
(1)求、;
(2)求证:数列是等差数列;
(3)令,问数列的前多少项的和最小?最小值是多少?
云南省2014年1月普通高中学业水平考试
数学试卷
[考生注意]:必须在答题卡上指定位置按规定要求作答,答在试卷上一律无效.
参考公式:
如果事件A、B互斥,那么.
球的表面积公式:,体积公式:,其中R表示球的体积.
柱体的体积公式:,其中S表示柱体的底面面积,h表示柱体的高.
锥体的体积公式:,其中S表示锥体的底面面积,h表示锥体的高.
选择题(共51分)
一、选择题:本大题共17个小题,每小题3分,共51分。在每小题给出的四个选项中,只有一项符合题目要求,请在答题卡相应的位置上填涂。
1. 设集合,,则下列关系正确的是
A. B. C. D.
2. 有一个几何体的三视图如下图所示,这个几何体是一个
A.棱台
B.棱锥
C.棱柱
D.圆柱
3. 已知向量,,则等于
A.1 B. C.2 D.
4.如图是某运动员在某个赛季得分的茎叶统计图,则该运动员得分的中位数是
A.2 B.3
C.22 D.23
5.函数的零点时
A.0 B. C. D.
6.已知一个算法,其流程图右图,则输出的结果是
A.10 B.11
C.8 D.9
7.在中,M时BC的重点,则等于
A. B. C. D.
8.如图 ,在边长为2的正方形内有一内切圆,现从
正方形内取一点P,则点P在圆内的概率为
A. B.
C. D.
9.下列函数中,以为最小正周期的是
A. B. C. D.
10. 在中,内角A、B、C的对边分别为a、b、c,若,,,则b等于
A.1 B. C. D.2
11.同时抛投两枚质地均匀的硬币,则两枚硬币均正面向上的概率为
A. B. C. D.
12.直线与直线的位置关系式
A.平行 B. 垂直 C. 相交但不垂直 D.重合
13.不等式的解集是
A. B. C. D.
14.已知函数,用秦九昭算法计算的值时,首先计算的最内层括号内一次多项式的值是
A. 1 B. 2 C. 3 D. 4
15. 已知函数,则下列说话正确的是
A. 为奇函数,且在上是增函数
B. 为奇函数,且在上是减函数
C. 为偶函数,且在上是增函数
D. 为偶函数,且在上是偶函数
16. 已知数列是公比为实数的等比数列,且,,则等于
A2 B. 3 C. 4 D. 5
17.已知直线l过点,圆C:,则直线l与圆C的位置关系是
A.相交 B. 相切 C.相交和相切 D.相离
非选择题(共49分)
二、 填空题:本大题共5个小题,每小题3分,共15分。请把答案写在答题卡相应的位置上。
18.某工厂生产A、B、C三种不同型号的产品,产品数列之比一次为2:3:5,现用分层抽样的方法抽出一个容量为n的样本,其中A种型号产品有16件,那么此样本的容量n= .
19.直线的纵截距是 .
20.化简= .
21. 若实数x,y满足约束条件:,则的最大值等于 .
22.函数在区间上的最大值是 .
三、解答题:本大题共4小题,共34分.解答应写出文字说明、证明过程或演算步骤.
23. (本小题满分8分)已知.
(1)求的值及的最大值;
(2)求的递减区间
24. (本小题满分8分)
如图所示,在三棱锥P-ABC中,E、F分别为AC、BC的中点。
(1)求证:;
(2)若,,求证:.
25. (本小题满分8分)
某商场的一种商品每件进价为10元,据调查知每日销售量m(件)与销售价x(元)之间的函数关系为,.设该商场日销售这种商品的利润为y(元).(单件利润=销售单价-进价;日销售利润=单件利润日销售量)
(1)求函数的解析式;
(2)求该商场销售这种商品的日销售利润的最大值.
26. (本小题满分10分)
已知正项数列的前n项和为,且
(1)求、;
(2)求证:数列是等差数列;
(3)令,问数列的前多少项的和最小?最小值是多少?
同课章节目录
