2021-2022学年浙江省各地人教版数学七年级上册3.4 实际问题与一元一次方程 期末试题分类选编(含解析)
文档属性
| 名称 | 2021-2022学年浙江省各地人教版数学七年级上册3.4 实际问题与一元一次方程 期末试题分类选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 776.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-15 21:28:37 | ||
图片预览



文档简介
3.4 实际问题与一元一次方程
1.(2022·浙江金华·七年级期末)《算学启蒙》中有一道题,原文是:良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之?译文为:跑的快的马每天走240里,跑的慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马x天可以追上慢马,可列方程( )
A.240x=150(x+12) B.240(x﹣12)=150x
C.240(x+12)=150x D.240x=150(x﹣12)
2.(2022·浙江宁波·七年级期末)甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点...若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后2分钟内,两人相遇的次数为( )
A.7 B.6 C.5 D.4
3.(2022·浙江金华·七年级期末)某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套.设安排x名工人生产螺钉,则下面所列方程正确的是( )
A.2×1000(26﹣x)=800x B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x D.1000(26﹣x)=800x
4.(2022·浙江舟山·七年级期末)某商品因换季准备打折销售,如果按定价的七五折出售,将亏本35元,而按定价的九五折出售,将赚25元.设这种商品的定价为x元,可列方程为( )
A.75%x-35=95%x+25 B.75%x+35=95%x+25
C.75%x-35=95%x-25 D.75%x+35=95%x-25
5.(2022·浙江绍兴·七年级期末)《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少 ”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字 已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的是( ).
A.x+2x+4x=34 685 B.x+2x+3x=34 685
C.x+2x+2x=34 685 D.x+x+x=34 685
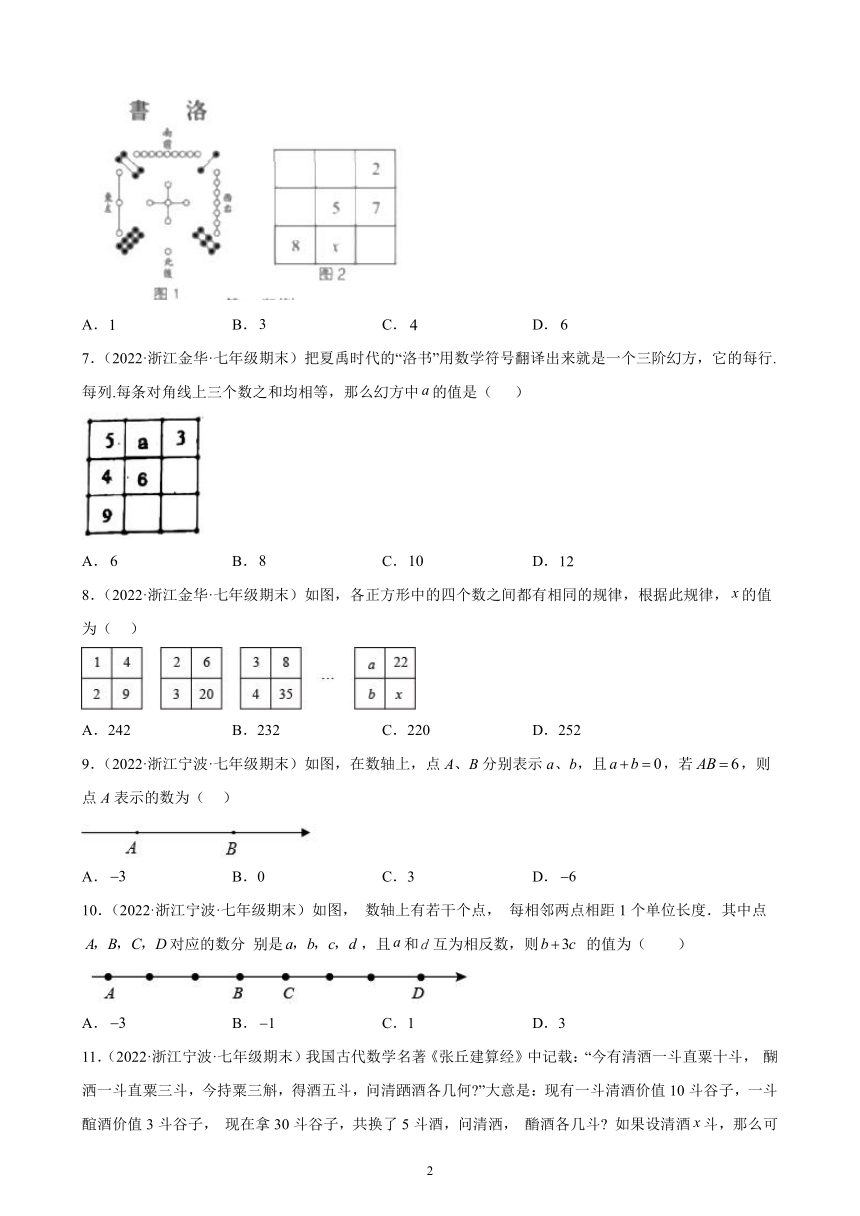
6.(2022·浙江绍兴·七年级期末)把这个数填入方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图),是世界上最早的“幻方”.图是仅可以看到部分数值的“九宫格”,则其中的值为:( )
A. B. C. D.
7.(2022·浙江金华·七年级期末)把夏禹时代的“洛书”用数学符号翻译出来就是一个三阶幻方,它的每行.每列.每条对角线上三个数之和均相等,那么幻方中的值是( )
A. B. C. D.
8.(2022·浙江金华·七年级期末)如图,各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
A.242 B.232 C.220 D.252
9.(2022·浙江宁波·七年级期末)如图,在数轴上,点A、B分别表示a、b,且,若,则点A表示的数为( )
A. B.0 C.3 D.
10.(2022·浙江宁波·七年级期末)如图, 数轴上有若干个点, 每相邻两点相距1个单位长度.其中点对应的数分 别是,且和互为相反数,则 的值为( )
A. B. C.1 D.3
11.(2022·浙江宁波·七年级期末)我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗, 醐洒一斗直粟三斗,今持粟三斛,得酒五斗,问清跴酒各几何 ”大意是:现有一斗清酒价值10斗谷子,一斗 酒价值3斗谷子, 现在拿30斗谷子,共换了5斗酒,问清洒, 酳酒各几斗 如果设清酒斗,那么可列方程为( )
A. B.
C. D.
12.(2022·浙江绍兴·七年级期末)某种商品每件的进价为120元,标价为180元.为了拓展销路,商店准备打折销售.若使利润率为20%,则商店应打________折.
13.(2022·浙江舟山·七年级期末)《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买一只羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设羊价为x钱,所列方程是_______.
14.(2022·浙江台州·七年级期末)某企业举办“**产品创新设计大赛”,设奖规定如下:
①参赛的员工均有奖,设一、二、三等奖.其中,一等奖的人数小于二等奖的人数,二等奖的人数小于三等奖的人数.
②奖金总额48000元,每个一等奖的奖金额是二等奖的3倍,是三等奖的6倍.若比赛共有8人参加,根据设奖规定,则每个三等奖的奖金额应是___元.
15.(2022·浙江宁波·七年级期末)中国古代数学著作《九章算术》有如下问题:“今有三人共车,二车空;二人共车,九人步,问人与车各几何?”意思是:今有3人坐一辆车,有2辆车是空的;2人坐一辆车,有9个人需要步行.问人与车各多少?若设车有辆,则根据题意可以列出关于的方程为__________.
16.(2022·浙江台州·七年级期末)小王和小李每天从地到地上班,小王坐公交车以的速度匀速行驶,小李开汽车以的速度匀速行驶.
(1)若他们同时从地出发,15分钟后,两人相距______;
(2)假设途中设有9个站点,,…,公交车在每个站点都停靠0.5分钟.
①若两车同时从地出发,则汽车比公交车早10.5分钟到达.求,两地的距离.
②若每相邻两个站点间(包含起点站和终点站)的距离相等,小王4:30坐公交车从地前往地,8分钟后小李开汽车也从地前往地,求小李追上小王的时刻.
17.(2022·浙江丽水·七年级期末)盲盒近来火爆,这种不确定的“盲盒”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共100盒,这两种盲盒的进价、售价如表所示:
类型 进价(元/盒) 售价(元/盒)
文具盲盒 16 20
Molly盲盒 36 52
(1)若采购共用去3400元,则两种盲盒各采购了多少盒?
(2)在(1)的条件下全部售完这100盒,那么玩具商店获利多少元?
(3)是否有一种采购方案使得销售完这100盒盲盒的总利润恰好为1400元?若能,请说出采购方案;若不能,证明理由.
18.(2022·浙江杭州·七年级期末)在一次知识竞赛中,甲、乙两班各有50位同学参加比赛,每位同学都需要完成三道题的答题,竞赛规则为:“答对一题得10分,不答或者答错扣10分”.
(1)请直接写出每位同学所有可能的得分情况;
(2)甲班的答题情况为:有2位同学全部答错,全对的人数是答对1题人数的3倍少6人,答对两题的人数是答对1题人数的2倍;乙班的答题情况为:没有同学全部答错,答对一题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲乙两班哪个班的得分更高,并说明理由.
19.(2022·浙江金华·七年级期末)为更好地营造“多读书、读好书、好读书”的书香校园氛围,学校图书馆向出版商邮购某系列图书.相关的书价折扣、邮费如下表所示.(注:总费用=总书价+总邮费)
数量 折扣 邮费
不超过10本 九折 7元
超过10本 八五折 优惠后总书价的10%
(1)已知书的单价为15元,需购书30本.
①若采用分次邮购,每次10本,共需总费用为 元;
②若采用一次性邮购,共需费用为 元.
(2)已知图书馆需购书的总数是10的整数倍,且超过10本.图书馆负责人发现分次邮购所需费用与一次性邮购所需费用相同,求书的单价是多少元?
20.(2022·浙江宁波·七年级期末)如图,在数轴上点O是原点,点A表示数,点B在点A的右侧,且.
(1)点B表示的数是______.
(2)若动点P从点A出发以2个单位/秒的速度沿着x轴正方向运动,当时,求点P运动的时间.
21.(2022·浙江金华·七年级期末)如图,数轴上点A,B分别表示数-6,12,C为AB中点.
(1)求点C表示的数.
(2)若点P为线段AB上一点,PC=2,求点P表示的数.
(3)若点D为线段AB上一点,在线段AB上有两个动点M,N,分别同时从点A,D出发,沿数轴正方向运动,点M的速度为4个单位每秒,点N的速度为3个单位每秒,当MN=1,NC=2时,求点D表示的数.
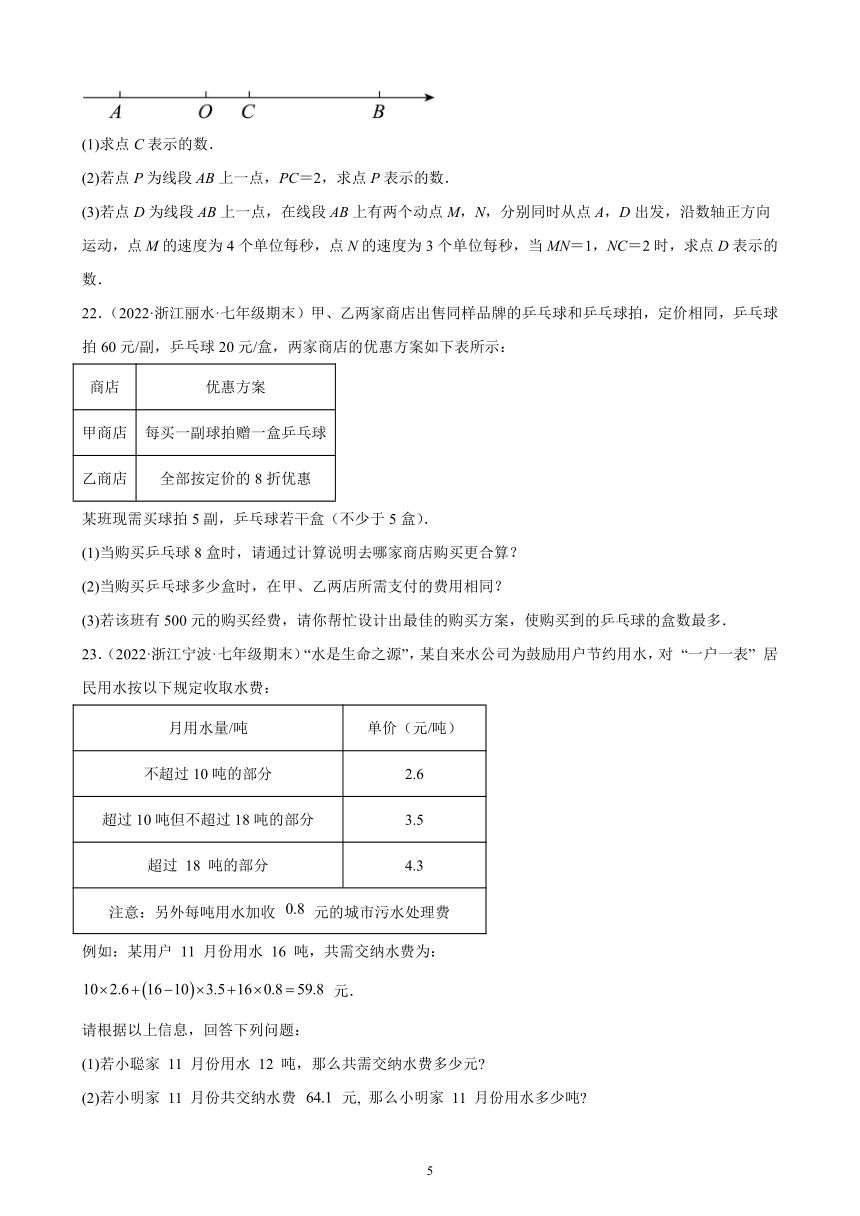
22.(2022·浙江丽水·七年级期末)甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,定价相同,乒乓球拍60元/副,乒乓球20元/盒,两家商店的优惠方案如下表所示:
商店 优惠方案
甲商店 每买一副球拍赠一盒乒乓球
乙商店 全部按定价的8折优惠
某班现需买球拍5副,乒乓球若干盒(不少于5盒).
(1)当购买乒乓球8盒时,请通过计算说明去哪家商店购买更合算?
(2)当购买乒乓球多少盒时,在甲、乙两店所需支付的费用相同?
(3)若该班有500元的购买经费,请你帮忙设计出最佳的购买方案,使购买到的乒乓球的盒数最多.
23.(2022·浙江宁波·七年级期末)“水是生命之源”,某自来水公司为鼓励用户节约用水,对 “一户一表” 居民用水按以下规定收取水费:
月用水量/吨 单价(元/吨)
不超过10吨的部分 2.6
超过10吨但不超过18吨的部分 3.5
超过 18 吨的部分 4.3
注意:另外每吨用水加收 元的城市污水处理费
例如:某用户 11 月份用水 16 吨,共需交纳水费为:
元.
请根据以上信息,回答下列问题:
(1)若小聪家 11 月份用水 12 吨,那么共需交纳水费多少元
(2)若小明家 11 月份共交纳水费 元, 那么小明家 11 月份用水多少吨
(3)若小聪和小明家 12 月份共用水 23 吨,共交纳水费 元,其中小聪家用水量少于 10 吨,那么小聪家和小明家 12 月份各用水多少吨
24.(2022·浙江宁波·七年级期末)为了平衡电力负荷,减少用电高峰时段用电和不必要的能源消耗,浙江省居民生活用电可申请“峰谷电”,两种收费标准如下:
未申请峰谷电即阶梯电价收员标准:
月用电总量 (单位:千瓦时) 电度电价 (单位:元/千瓦时)
230 及以下部分
超过230至400部分
超过400部分
峰谷电收费标准:
高峰电价 低谷电价
元/千瓦时 元/千瓦时
月用电总量超过230千瓦时至400千瓦时 部分加收元/千瓦时; 月用电总登超过 400千瓦时部分加收元/千瓦时
如:某用户月用电总量300千瓦时,其中高峰时用电100千瓦时, 低谷时用电200千瓦时.如果不申请峰谷电则需费用;若申请峰谷电则需费用 .
(1)小明家5月份用电总量为400千瓦时,其中峰时用电量为150千瓦时,低谷时间段用电量为250千瓦时,如不申请峰谷电,应付电费______元;若申请峰谷电,应付电费______元;
(2)小强家未申请峰谷电,8月份一共交电费元,求小强家8月份的用电总量;
(3)小强听小朋介绍峰谷电节能且收费便宜,于是9月份就申请了峰谷电, 9月份用电总量是330千瓦时,经计算申请峰谷电后比申请前节约了元,求小强家9月份的峰时用电量为多少
25.(2022·浙江丽水·七年级期末)如图,将1,2,3,…,40这40个数按照下表进行排列,现用一个Z字框(图中阴影部分)框住表中的4个数,移动该框,设框中最小的数为.
(1)请用含的代数式表示框中4个数的和.
(2)框中4个数的和可能是132吗?若能,请求出最小的数.
26.(2022·浙江舟山·七年级期末)下表是某网约车公司的专车计价规则
计费项目 起租价 里程费 时长费
单价 10元 2.5元/千米 1元/分
注:应付车费=起租价+里程费+时长费,其中起租价10元含5千米里程费和10分钟时长费.
例如:若坐专车行驶里程为12千米,行车时间为20分钟,则需付车费:
(元).
若坐专车行驶里程为4千米,行车时间为12分钟,则需付车费:(元).
(1)若小聪乘坐专车,行车里程为20千米,行车时间为30分,则需付车费_______元;
(2)若小聪乘坐专车,行车里程为()千米,平均时速为40千米/时,则小聪应付车费多少元?(用含的代数式表示)
(3)小聪与小明各自乘坐专车从家去吾悦广场,由于堵车,小聪乘坐了12分钟,小明乘坐了20分钟,两车车费之和为47元,里程之和为15千米(其中小聪的行车里程不超过5千米).那么这两辆专车此次的行驶路程各为多少千米?
27.(2022·浙江嘉兴·七年级期末)庆祝建党100周年,学校七、八年级开展“追寻建党足迹,传承红船精神”的革命纪念馆研学活动.根据防控要求,入馆前需体温检测.其中A通道是电子测温,B通道是人工测温,A通道每分钟通过的人数是B通道的2倍.已知该校七、八年级学生人数分别为96人和144人,七年级学生进馆时,同时开通了A、B两通道,经过4分钟,学生全部进馆.
(1)分别求A、B两通道每分钟通过的人数.
(2)八年级学生进馆时,先同时开通A、B两通道,1分钟后增开一个人工测温通道C,已知C通道每分钟通过的人数是B通道的,求八年级学生全部进馆所需时间.
28.(2022·浙江湖州·七年级期末)如图,数轴上的点从左往右依次A,B,C对应的数分别为a,b,c,且|a+3|+|b-6|=0,AB的距离比BC的距离大4,动点P从点A出发沿数轴以每秒6个单位的速度向右运动,同时动点Q从点B出发沿数轴以每秒2个单位的速度一直向右运动,当点P运动到点C之后立即以原速沿数轴一直向左运动,设运动的时间为t秒.
(1)填空:a= ,b= ,点Q在数轴上所表示的数为 (用含t的代数式表示).
(2)当动点P从点A运动到点C过程中,Q点是PC的中点时,则点Q在数轴上所表示的数是多少?
(3)在整个运动过程中,是否存在t使得QB=2PC,若存在,求出t的值,若不存在,请说明理由.
29.(2022·浙江金华·七年级期末)如图,自行车每节链条的长度为2.3cm,交叉重叠部分的圆的直径为0.7cm.
(1)2节链条长 cm,5节链条长 cm,n节链条长 cm;
(2)如果一辆自行车的链条的总长度为99.9cm,求这辆自行车上有几节链条?
30.(2022·浙江宁波·七年级期末)对于数轴上给定的两点M,N(M在N的左侧),若数轴上存在点P,使得,则称点P为点M,N的“k和点”.例如,如图1,点M,N表示的数分别为0,2,点P表示的数为1,因为,所以点P是点M,N的“4和点”.
(1)如图2,已知点A表示的数为,点B表示的数为2.
①若点O表示的数为0,点O为点A,B的“k和点”,则k的值______.
②若点C在线段AB上,且点C是点A,B的“5和点”,则点C表示的数为______.
③若点D是点A,B的“k和点”,且,求k的值.
(2)数轴上点E表示的数为a,点F在点E的右侧,,点T是点E,F的“6和点”,请求出点T表示的数t的值(用含a的代数式表示).
参考答案:
1.A
【解析】设快马x天可以追上慢马,则慢马跑了(x+12)天,根据路程=速度×时间结合两匹马跑过的路程相等,即可得出关于x的一元一次方程,此题得解.
设快马x天可以追上慢马,则慢马跑了(x+12)天,
依题意,得:240x=150(x+12).
故选:A.
本题考查了一元一次方程的应用,正确理解题意,找到等量关系并列出方程是关键.
2.C
【解析】根据题意,首先计算得甲、乙两运动员每次相遇的时间间隔为:,设两人相週的次数为,根据一元一次方程的性质列方程并求解,即可得到答案.
根据题意,甲、乙两运动员每次相遇的时间间隔为:
设两人相遇的次数为
∵起跑后时间总共为2分钟,即120 s
∴
∴
根据题意,两人相遇的次数为整数
∴,即两人相遇的次数为5次
故选:C.
本题考查了一元一次方程的知识;解题的关键是熟练掌握一元一次方程的性质,从而完成求解.
3.C
【解析】此题等量关系为:2×螺钉总数=螺母总数,据此设未知数列出方程即可.
解:设安排x名工人生产螺钉,则(26-x)人生产螺母,由题意得
1000(26-x)=2×800x,
故C答案正确
故选C
4.D
【解析】设这种商品的定价是x元.根据定价的7.5折出售将赔35元和定价的9.5折出售将赚25元,分别表示出进价,从而列方程求解.
解:设这种商品的定价是x元.
根据题意,得75%x+35=95%x-25.
故选:D.
本题考查了由实际问题抽象出一元一次方程的知识,解题的关键是根据题意找到等量关系,这是列方程的关键.
5.A
【解析】设他第一天读x个字,根据题意列出方程解答即可.
解:设他第一天读x个字,根据题意可得:x+2x+4x=34685,
故选A.
此题考查由实际问题抽象出一元一次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.
6.A
【解析】根据题意求出“九宫格”中的y,再求出x即可求解.
如图,依题意可得2+5+8=2+7+y
解得y=6
∴8+x+6=2+5+8
解得x=1
故选A.
此题主要考查一元一次方程的应用,解题的关键是根据题意得到方程求解.
7.C
【解析】根据题意列出一元一次方程,即可求解.
依题意得5+4+9=5+3+a
解得a=10
故选C.
此题主要考查一元一次方程的应用,解题的关键是根据题意列出方程即可求解.
8.D
【解析】观察所给数字,利用正方形中四个数字之间的关系总结出规律,即可求解.
解:观察题目所给数字可得:第n个正方形中,左上角的数字为n,左下角的数字为,右上角的数字为,右下角的数字为左下角、右上角两个数字的积,再加上左上角的数字.
∴为第a个正方形,,
解得:,
∴,
∴,
故选D.
本题属于数字规律题,考查了列代数式、一元一次方程的应用,能够利用正方形中四个数字之间的关系总结出规律是解题的关键.
9.A
【解析】由AB的长度结合A、B表示的数互为相反数,即可得出A,B表示的数
解:∵
∴,两点对应的数互为相反数,
∴可设表示的数为,则表示的数为,
∵
∴,
解得:,
∴点表示的数为-3,
故选:A.
本题考查了绝对值,相反数的应用,关键是能根据题意得出方程.
10.C
【解析】根据各点在数轴上的位置,把b、c、d都用含a的式子表示出来,根据a和d互为相反数求出a的值,再求出b+3c的值即可.
解:由图可知:b=a+3,c=a+4,d=a+7,
∵a和d互为相反数,
∴a+d=0,即a+a+7=0,
∴a= 3.5,
∴b+3c=a+3+3(a+4)=4a+15=1.
故选:C.
本题考查了数轴,结合图形找出a、b、c、d之间的数量关系是解题的关键.
11.A
【解析】根据题意直接列方程即可.
解:根据题意,得:10x+3(5-x)=30,
故选:A.
本题考查一元一次方程的应用,理解题意,正确列出方程是解答的关键.
12.八
【解析】打折销售后要保证打折后利率为20%,因而可以得到不等关系为:利润率=20%,设可以打x折,根据不等关系列出不等式求解即可.
解:设应打x折,
则根据题意得:(180×x×10%-120)÷120=20%,
解得:x=8.
故商店应打八折.
故答案为:八.
本题考查一元一次方程的实际应用,解题关键是读懂题意,找到符合题意的等量关系式,同时要注意掌握利润率的计算方法.
13.
【解析】设羊价为x钱,根据题意可得合伙的人数为或,由合伙人数不变可得方程.
解:设羊价为x钱,
根据题意可得方程:,
故答案为:.
本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,找到等量关系,列出相应的方程.
14.3200或3000##3000或3200
【解析】设获一、 二、 三等奖的人数分别为a、b、c,根据①中题设求得a、b、c,再设每个三等奖的奖金额是x元,则每个一等奖的奖金额是6x,每个二等奖的奖金额是2x,根据题意列出方程求解即可.
解:设获一、 二、 三等奖的人数分别为a、b、c,
由题意,得:a+b+c=8,且0<a<b<c,a、b、c均为正整数,
∴a=1,b=2,c=5或a=1,b=3,c=4,
设每个三等奖的奖金额是x元,则每个一等奖的奖金额是6x,每个二等奖的奖金额是2x,
根据题意,得:6x+2×2x+5x=48000或6x+3×2x+4x=48000,
解得:x=3200或x=3000,
答:每个三等奖的奖金额应是3200元或3000元,
故答案为:3200或3000.
本题考查一元一次方程的应用,理解题意,正确列出方程并求得a、b、c的值是解答的关键.
15.3(x-2)=2x+9
【解析】设车为x辆,根据人数不变,即可得出关于x的一元一次方程,此题得解.
解:设车有x辆,则人有3(x-2)人,
依题意,得:3(x-2)=2x+9.
故答案为:3(x-2)=2x+9.
本题考查了一元一次方程的应用以及数学常识,找准等量关系,正确列出一元一次方程是解题的关键.
16.(1)2.5
(2)①20km;②小李追上小王的时刻为4:48.
【解析】(1)先求出小王和小李在15分钟内的路程,然后求得两个间的距离;
(2)①先设A、B两地相距x千米,然后分别用含有x的式子表示两人从A地到B地的时间,再结合“汽车比公交车早10.5分钟到达”列出方程求解,即可得到A、B两地间的距离;
②先由①得到每两个站点间的距离,然后计算得到公交车在每两个站点间的时间,进而初步判断8分钟后公交车的位置,然后设时间为m分钟,再分段进行讨论即可.
(1)
解:15分钟=0.25小时,
∴小王的路程为40×0.25=10(km),
小李的路程为50×0.25=12.5(km),
∴两人间的距离为12.5﹣10=2.5(km),
故答案为:2.5.
(2)
解:①设两地距离为x千米,则小李的从A地到B地的时间为 小时,小王的时间为 小时,
∵汽车比公交车早10.5分钟到达,
∴,
解得:x=20,
∴A、B两地相距20千米.
②由①得,A、B两地相距20千米,
∵每两个站点间的距离相等,
∴每两个站点间的距离为20÷10=2(千米),
∴小王经过两个站点间的时间为2÷40=0.05小时=3分钟,
∵3+0.5+3+0.5=7<8,
∴8分钟时,公交车在P2与P3之间,
设小李经过m分钟追上小王,
当小李在P2与P3之间追上小王,即m≤2时,
,
解得:m=28(舍);
当小李在P3与P4之间追上小王,即2.5<m≤5.5时,
,
解得:m=26(舍);
当小李在P4与P5之间追上小王,即6<m≤9时,
,
解得:m=24(舍);
当小李在P5与P6之间追上小王,即9.5<m≤12.5时,
,
解得:m=22(舍);
当小李在P6与P7之间追上小王,即13<m≤16时,
,
解得:m=20(舍);
当小李在P7与P8之间追上小王,即16.5<m≤19.5时,
,
解得:m=18;
∴经过18分钟,小李追上小王,
此时的时刻为4:48.
本题考查了一元一次方程的应用,解题的关键是会利用“路程=速度×时间”进行相关时间和路程的表示和会将时间单位进行转化.
17.(1)文具店采购了文具盲盒10盒,Molly盲盒90盒;
(2)销售完这100盒盲盒,文具店共获利1480元;
(3)销售完这100个盲盒的总利润不可能恰好为1400元.
【解析】(1)设文具店分别采购文具盲盒x盒,Molly盲盒盒,利用进价乘以件数算出总采购额,列出方程求解;
(2)用售价减进价得到单件利润,乘以(1)中的件数,得出总利润;
(3)设文具店分别采购文具盲盒m盒,Molly盲盒盒,用单件利润乘以件数,令两种盲盒的利润和为1400元,列方程求解.
(1)
解:设文具店分别采购文具盲盒x盒,Molly盲盒盒,
由题意得:,
解得,
(盒),
答:文具店采购了文具盲盒10盒,Molly盲盒90盒;
(2)
(元),
答:销售完这100盒盲盒,文具店共获利1480元;
(3)
设文具店分别采购文具盲盒m盒,Molly盲盒盒,
由题意得:,
解得,
∵m为整数,
∴不合题意,
答:销售完这100个盲盒的总利润不可能恰好为1400元.
本题考查一元一次方程的应用,解题的关键是找到题目中的等量关系列出方程进行求解.
18.(1)每位同学所有可能的得分情况是-30分、-10分、10分和30分;
(2)①甲班全部答对的人数是21人;②乙班得分更高.
【解析】(1)根据竞赛的得分规则可得答案;
(2)①设甲班答对1题的有x人,根据题意列出方程,解方程可得答案;
②首先算出甲班的得分,设乙班全部答对的有a人,答对1题的有b人,答对2题的有(a-3b)人,整理可得乙班的得分,再比较可得结论.
(1)
解:若只答对1题,则不答或答错2题,得分为:1×10-2×10=-10,
若只答对2题,则不答或答错1题,得分为:2×10-1×10=10,
若只答对3题,得分为:3×10=30,
若不答或答错3题,得分为:0-3×10=-30,
答:每位同学所有可能的得分情况是-30分、-10分、10分和30分;
(2)
解:①设甲班答对1题的有x人,
由题意得,2+(3x-6)+2x+x=50,
解得x=9,
3×9-6=21(人),
答:甲班全部答对的人数是21人;
②乙班得分更高.
由题意得,甲班答对3题有21人,答对2题的有18人,答对1题的有9人,全部答错的有2人,
故甲班的得分为21×30+18×10-9×10-2×30=660(分),
设乙班全部答对的有a人,答对1题的有b人,答对2题的有(a-3b)人,
所以a+b+(a-3b)=50,
即a-b=25,
故乙班得分为30a+10(a-3b)-10b=40(a-b)=1000(分),
1000>660,
答:乙班得分更高.
本题考查了一元一次方程的实际运用,整式加减的应用,找到等量关系列出方程是解决问题的关键.
19.(1)①426;②420.75
(2)书的单价是20元
【解析】(1)①根据表格中不超过10本的方案,可以解答本题;②根据表格中超过10本的方案,可以解答本题;
(2)设书的单价为x元,购书数量10a本(a是大于1的正整数),根据题意两种方案的费用一样建立等式求解即可.
(1)
解:①若采用分次邮购,每次10本,
根据题意有:(元),
②若采用一次性邮购,则
(元),
故答案为:426,420.75;
(2)
解:设书的单价为x元,购书数量10a本(a是大于1的正整数),根据题意得:
,
即:,
解得:x=20,
答:书的单价是20元.
本题考查一元一次方程的应用,解题的关键是明确题意,列出相应的方程求解即可.
20.(1)10
(2)3.5秒或8.5秒
【解析】(1)根据数轴上两点间的距离列式计算;
(2)设点P运动时间为t秒,然后利用数轴上两点间距离公式及OB=2BP列方程求解.
(1)
解:∵点A表示数 2,点B在点A的右侧,且AB=12,
∴ 2+12=10,
∴点B表示的数为10,
故答案为:10;
(2)
解:设点P运动时间为t秒,则在运动过程中点P所表示的数为 2+2t,
∴BP=|10 ( 2+2t)|=|12 2t|,
由题意,可得:10=2|12 2t|,
解得:t=3.5或t=8.5,
故当OB=2BP时,点P运动的时间为3.5秒或8.5秒.
本题考查了一元一次方程的应用,理解数轴上两点间距离结合方程思想解题是关键.
21.(1)3
(2)5或1
(3)-3.5或-2.5
【解析】(1)设点C表示的数为x,根据点C为AB中点,列出方程求解即可;
(2)设点P表示的数为m,根据两点间距离公式可列方程求解即可;
(3)分点N在点C的左侧和右侧两种情况讨论求解即可.
(1)
设点C表示的数为x,
∵点A表示的数为-6,点B表示的数为12,且点C为AB的中点
∴
解得,
所以,点C表示的数为:3;
(2)
设点P表示的数为m,
∵点C表示的数为3,且PC=2
∴
解得,或
∴点P表示的数为:5或1;
(3)
分两种情况:
①当点N在点C左侧时,如图,
∵,且点C表示的数为3
∴此时点N表示的数为:3-2=1
又MN=1
∴M表示的数为:1-1=0
∴
∴点M运动的时间为秒,
∴点N的运动时间也为1.5秒
∴个单位,
∴点D表示的数为:1-4.5=-3.5;
②当点N在点C的右侧时,如图,
∵,且点C表示的数为3
∴此时点N表示的数为:3+2=5
又MN=1
∴M表示的数为:5-1=4
∴
∴点M运动的时间为秒,
∴点N的运动时间也为2.5秒
∴个单位,
∴点D表示的数为:5-7.5=-2.5;
综上,点D表示的数为:-3.5或-2.5
本题考查一次方程应用及数轴上点表示的数,解题的关键是找准等量关系,正确列出一元一次方程.
22.(1)去甲商店购买更合算
(2)10盒
(3)在甲商店购买5副球拍获赠5盒乒乓球,再在乙商店购买12盒乒乓球.
【解析】(1)利用总价=单价×数量,结合两家商店给出的优惠方案,即可分别求出去甲、乙两商店购买所需费用,比较后即可得出结论;
(2)设当购买乒乓球x盒时,在甲、乙两店所需支付的费用相同,利用总价=单价×数量,结合两家商店给出的优惠方案及在两家商店购买所需费用相同,即可得出关于x的一元一次方程,解之即可得出结论;
(3)由甲、乙两家商店的优惠方案可得出最佳的购买方案为:在甲商店购买5副球拍获赠5盒乒乓球,再在乙商店购买12盒乒乓球.
(1)
解:去甲商店购买所需费用为60×5+20×(8-5)=360(元);
去乙商店购买所需费用为(60×5+20×8)×80%=368(元).
∵360<368,
∴去甲商店购买更合算.
(2)
解:设当购买乒乓球x盒时,在甲、乙两店所需支付的费用相同,
依题意得:60×5+20(x-5)=(60×5+20x)×80%,
解得:x=10.
(3)
解:甲店购买5副球拍时赠送5盒乒乓球,再次购买乒乓球需要按原价购买,而乙商店所有商品均按定价的8折优惠,
∴在甲商店购买5副球拍,赠送5盒乒乓球,剩余的钱再取乙商店购买乒乓球.
(500-60×5)÷(20×80%)=200÷16=12.5(盒).
∴最佳的购买方案为:在甲商店购买5副球拍获赠5盒乒乓球,再在乙商店购买12盒乒乓球.
本题考查了一元一次方程的应用以及有理数的混合运算,解题的关键是:(1)利用总价=单价×数量,结合两家商店给出的优惠方案,分别求出在甲、乙两家商店购买所需费用;(2)找准等量关系,正确列出一元一次方程;(3)根据两家商店给出的优惠方案,找出最佳的购买方案.
23.(1)共需交纳水费42.6元
(2)小明家 11 月份用水17吨
(3)小聪家12 月份用水9吨,小明家 12 月份用水14吨
【解析】(1)根据收费标准列式计算即可;
(2)设小明家11月份用水x吨,先判断x<18,再列方程求解;
(3)设12月份小聪家用水y吨,则小明家用水(23-y)吨,且y<10,分两种情况:当0(1)
解:需交纳水费(元);
(2)
解:设小明家11月份用水x吨,
∵>64.1,
∴x<18,
∴,
解得x=17,
答:小明家 11 月份用水17吨;
(3)
解:设12月份小聪家用水y吨,则小明家用水(23-y)吨,且y<10,
当018,
,解得(舍去);
当时,10<23-y18,
,解得y=9,
∴23-9=14
答:小聪家12 月份用水9吨,小明家 12 月份用水14吨.
此题考查了分段收费问题的一元一次方程的实际应用,正确理解各段的收费标准列出方程是解题的关键.
24.(1)224.5 ;166.5
(2)小强家8月份用电总量500千瓦时
(3)小强家9月份峰时用电100千瓦时
【解析】(1)根据两种计费方式进行求解即可;
(2)可设小强家8月份用电总量为x千瓦时,根据未申请峰谷电的方式进行列方程计算即可;
(3)根据两种方式相差54.5元可列出方程求解.
(1)解:不申请峰谷电,应付电费为:0.54×230+0.59×(400﹣230)=224.5(元),请峰谷电,应付电费为:0.57×150+0.29×250+0.05×(400﹣230)=166.5(元),故答案为:224.5,166.5;
(2)解:∵308.5>224.5,∴用电量超过400千瓦时,设小强家8月份用电总量为x千瓦时,依题意得:0.54×230+0.59×(400﹣230)+0.84(x﹣400)=308.5,解得:x=500,答:小强家8月份用电总量为500千瓦时;
(3)解:设小强家9月份的峰时用电量为y千瓦时,依题意得:0.54×230+0.59×(330﹣230)﹣[0.57y+0.29(330﹣y)+0.05×(330﹣230)]=54.5,解得:y=100,答:小强家9月份的峰时用电量为100千瓦时.
本题主要考查一元一次方程的应用,解答的关键是理解清楚题意找到等量关系.
25.(1)4x+24
(2)能,最小的数为27
【解析】(1)若框中最小的一个数为x,则其它四个数分别是x+1、x+11、x+12.然后求和即可;
(2)根据所给的数的和列方程计算,如果结果不是整数,则应舍去.
(1)
解:设框中最小的数为x,则
x+x+1+x+11+x+12=4x+24;
∴框中4个数的和为x+24.
(2)
解:根据题意,得4x+24=132.
解得x=27.
观察表格中的数据知,x=27符合题意.
答:能,最小的数是27.
此题考查了一元一次方程的应用,列代数式和数字的变化规律,关键是根据所给的数的和列方程计算解答.
26.(1)67.5;(2);(3)小聪乘坐4千米,小明乘坐11千米
【解析】(1)按收费标准计算应付车费=起租价+15千米里程费+20分钟时长费即可;
(2)先计算是否收时长费,应付车费=起租价+(x-5)千米里程费+长费化简即可;
(3)设小聪乘坐(x<5)千米,则小明乘坐千米,先求出每人的费用小聪乘坐(x<5)千米费用是起租价+时长费=10+1×(12-10)元,小明乘坐千米费用是起租价+里程费+时长费=10+2.5×(15-x-5)+1×(20-10)元,利用费用之和47构造方程,解方程即可.
解:(1)10+(20-5)×2.5+(30-10)×1,
=,
(元),
故答案为:67,5;
(2)∵,所以时间超过10分钟,
∴;
(3)设小聪乘坐(x<5)千米,则小明乘坐千米,
小聪乘坐(x<5)千米费用是起租价+时长费=10+1×(12-10)元,
小明乘坐千米费用是起租价+里程费+时长费=10+2.5×(15-x-5)+1×(20-10)元,
根据题意,得:
,
整理的2.5x=10,
解得,
∴(千米),
答:小聪乘坐4千米,小明乘坐11千米.
本题考查网约车计费列代数式与简单方程,掌握计费种类与标准,以及计费公式,利用路程之和15千米设元,利用费用之和47构造方程是解题关键.
27.(1)A通道每分钟通过16人,B通道每分钟道过8人
(2)八年级学生全部进馆需5分钟
【解析】(1)设B通道每分钟通过x人,根据题意列一元一次方程解方程求解即可;
(2)设八年级学生全部进馆需y分钟,根据题意列一元一次方程解方程求解即可;
(1)
解:设B通道每分钟通过x人,根据题意得:
,解得,则
答:A通道每分钟通过16人,B通道每分钟道过8人.
(2)
解:设八年级学生全部进馆需y分钟,根据题意得:
,解得
答:八年级学生全部进馆需5分钟.
本题考查了一元一次方程的应用,根据题意列出一元一次方程是解题的关键.
28.(1)-3,6,6+2t
(2)点Q在数轴上所表示的数是10
(3)存在,当时,;当时,
【解析】(1)根据绝对值的非负性可求出a、b的值,利用求出Q点运动的距离,再加上B所表示的数,即可求解;
(2)根据题意,,则,解方程即可求出Q为PC中点时间t,再代入即可求解;
(3),根据题意解出方程,分情况讨论即可.
(1)
解:∵|a+3|+|b-6|=0,
∴a+3=0,b-6=0,
∴ ,
∴B表示的数为6,
∵点Q从点B出发沿数轴以每秒2个单位的速度一直向右运动,
∴ ,
∴点Q在数轴上所表示的数为 ;
(2)
由(1)知A表示的数为-3,B表示的数为6,
∴ ,
∵ ,
∴ ,且C在B的右侧,
∴C点表示的数为 ,
∴ ,
∴ ,
∵ ,
∴,
∴ ,
当 时点Q在数轴上所表示的数为;
当 时点P的运动轨迹为A向C再向A,故舍去,
故当Q为PC中点时,Q所表示的数为10;
(3)
,
当时,即 ,
∴ ,
P到达C点时 ,
∴当时,P点由A向C运动,
即 时, ,
当,P点由A向C再向A运动,
即时, .
本题主要考查了一元一次方程的应用,数轴和绝对值,解题的关键是读懂题意,找到等量关系,列出方程并解答,难度较大.
29.(1)3.9;8.7;1.6n+0.7
(2)62
【解析】(1)根据题目中链条的结构及计算规律即可得出结果;
(2)将链条长度等于99.9cm代入(1)中解析式中求解即可得.
(1)
解:根据图形可得出:
2节链条的长度为:
2.3×2-0.7=3.9cm,
3节链条的长度为:
2.3×3-0.7×2=5.5cm,
4节链条的长度为:
2.3×4-0.7×3=7.1cm,
5节链条的长度为:
2.3×5-0.7×4=8.7cm,
…
n节链条的长度为:
2.3×n-0.7×(n-1)=1.6n+0.7cm,
故答案为:3.9;8.7;1.6n+0.7;
(2)
解:由题意得:1.6n+0.7=99.9,
解得:n=62,
答:这辆自行车有62节链条.
本题主要考查规律探索及解一元一次方程,理解题意,找出相应规律是解题关键.
30.(1)①8;②1.5;③或20
(2)t的值为或
【解析】(1)①根据定义得OA+3OB=k,计算即可;
②设点C表示的数为c,根据题意列方程求解;
③分两种情况:当点D在AB之间,点D位于点B右侧,求出AD、BD,根据公式即可求出k;
(2)分三种情况:①当点T位于点E左侧,②当点T在线段EF上时,③当点T位于点F右侧,列方程解答 .
(1)
解:①∵点O为点A,B的“k和点”,
∴OA+3OB=k,
∴点A表示的数为,点B表示的数为2.
∴OA=2,OB=2,
∴k=8,
故答案为:8;
②设点C表示的数为c,
∵点C是点A,B的“5和点”,
∴AC+3BC=5,
∴c+2+3(2-c)=5,
解得c=1.5,
故答案为:1.5;
③当点D在AB之间,
∵,
∴,,
∴;
点D位于点B右侧,
∵,
∴,
∴,
∴.
故k的值为或20;
(2)
解:①当点T位于点E左侧,即时,显然不满足条件.
②当点T在线段EF上时,
∵,
∴.
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴.
③当点T位于点F右侧时,
∵,
∴,
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴,
综上所述,t的值为或.
此题考查了数轴上两点之间的距离,一元一次方程的实际应用,解题中运用分类思想解决问题是解题的关键.
1.(2022·浙江金华·七年级期末)《算学启蒙》中有一道题,原文是:良马日行二百四十里,驽马日行一百五十里.驽马先行一十二日,问良马几何追及之?译文为:跑的快的马每天走240里,跑的慢的马每天走150里.慢马先走12天,快马几天可以追上慢马?设快马x天可以追上慢马,可列方程( )
A.240x=150(x+12) B.240(x﹣12)=150x
C.240(x+12)=150x D.240x=150(x﹣12)
2.(2022·浙江宁波·七年级期末)甲、乙两运动员在长为100m的直道AB(A,B为直道两端点)上进行匀速往返跑训练,两人同时从A点起跑,到达B点后,立即转身跑向A点,到达A点后,又立即转身跑向B点...若甲跑步的速度为5m/s,乙跑步的速度为4m/s,则起跑后2分钟内,两人相遇的次数为( )
A.7 B.6 C.5 D.4
3.(2022·浙江金华·七年级期末)某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套.设安排x名工人生产螺钉,则下面所列方程正确的是( )
A.2×1000(26﹣x)=800x B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x D.1000(26﹣x)=800x
4.(2022·浙江舟山·七年级期末)某商品因换季准备打折销售,如果按定价的七五折出售,将亏本35元,而按定价的九五折出售,将赚25元.设这种商品的定价为x元,可列方程为( )
A.75%x-35=95%x+25 B.75%x+35=95%x+25
C.75%x-35=95%x-25 D.75%x+35=95%x-25
5.(2022·浙江绍兴·七年级期末)《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少 ”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字 已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的是( ).
A.x+2x+4x=34 685 B.x+2x+3x=34 685
C.x+2x+2x=34 685 D.x+x+x=34 685
6.(2022·浙江绍兴·七年级期末)把这个数填入方格中,使其任意一行,任意一列及两条对角线上的数之和都相等,这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图),是世界上最早的“幻方”.图是仅可以看到部分数值的“九宫格”,则其中的值为:( )
A. B. C. D.
7.(2022·浙江金华·七年级期末)把夏禹时代的“洛书”用数学符号翻译出来就是一个三阶幻方,它的每行.每列.每条对角线上三个数之和均相等,那么幻方中的值是( )
A. B. C. D.
8.(2022·浙江金华·七年级期末)如图,各正方形中的四个数之间都有相同的规律,根据此规律,的值为( )
A.242 B.232 C.220 D.252
9.(2022·浙江宁波·七年级期末)如图,在数轴上,点A、B分别表示a、b,且,若,则点A表示的数为( )
A. B.0 C.3 D.
10.(2022·浙江宁波·七年级期末)如图, 数轴上有若干个点, 每相邻两点相距1个单位长度.其中点对应的数分 别是,且和互为相反数,则 的值为( )
A. B. C.1 D.3
11.(2022·浙江宁波·七年级期末)我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗, 醐洒一斗直粟三斗,今持粟三斛,得酒五斗,问清跴酒各几何 ”大意是:现有一斗清酒价值10斗谷子,一斗 酒价值3斗谷子, 现在拿30斗谷子,共换了5斗酒,问清洒, 酳酒各几斗 如果设清酒斗,那么可列方程为( )
A. B.
C. D.
12.(2022·浙江绍兴·七年级期末)某种商品每件的进价为120元,标价为180元.为了拓展销路,商店准备打折销售.若使利润率为20%,则商店应打________折.
13.(2022·浙江舟山·七年级期末)《九章算术》是我国古代数学名著,卷七“盈不足”中有题译文如下:今有人合伙买一只羊,每人出5钱,会差45钱;每人出7钱,会差3钱.问合伙人数、羊价各是多少?设羊价为x钱,所列方程是_______.
14.(2022·浙江台州·七年级期末)某企业举办“**产品创新设计大赛”,设奖规定如下:
①参赛的员工均有奖,设一、二、三等奖.其中,一等奖的人数小于二等奖的人数,二等奖的人数小于三等奖的人数.
②奖金总额48000元,每个一等奖的奖金额是二等奖的3倍,是三等奖的6倍.若比赛共有8人参加,根据设奖规定,则每个三等奖的奖金额应是___元.
15.(2022·浙江宁波·七年级期末)中国古代数学著作《九章算术》有如下问题:“今有三人共车,二车空;二人共车,九人步,问人与车各几何?”意思是:今有3人坐一辆车,有2辆车是空的;2人坐一辆车,有9个人需要步行.问人与车各多少?若设车有辆,则根据题意可以列出关于的方程为__________.
16.(2022·浙江台州·七年级期末)小王和小李每天从地到地上班,小王坐公交车以的速度匀速行驶,小李开汽车以的速度匀速行驶.
(1)若他们同时从地出发,15分钟后,两人相距______;
(2)假设途中设有9个站点,,…,公交车在每个站点都停靠0.5分钟.
①若两车同时从地出发,则汽车比公交车早10.5分钟到达.求,两地的距离.
②若每相邻两个站点间(包含起点站和终点站)的距离相等,小王4:30坐公交车从地前往地,8分钟后小李开汽车也从地前往地,求小李追上小王的时刻.
17.(2022·浙江丽水·七年级期末)盲盒近来火爆,这种不确定的“盲盒”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共100盒,这两种盲盒的进价、售价如表所示:
类型 进价(元/盒) 售价(元/盒)
文具盲盒 16 20
Molly盲盒 36 52
(1)若采购共用去3400元,则两种盲盒各采购了多少盒?
(2)在(1)的条件下全部售完这100盒,那么玩具商店获利多少元?
(3)是否有一种采购方案使得销售完这100盒盲盒的总利润恰好为1400元?若能,请说出采购方案;若不能,证明理由.
18.(2022·浙江杭州·七年级期末)在一次知识竞赛中,甲、乙两班各有50位同学参加比赛,每位同学都需要完成三道题的答题,竞赛规则为:“答对一题得10分,不答或者答错扣10分”.
(1)请直接写出每位同学所有可能的得分情况;
(2)甲班的答题情况为:有2位同学全部答错,全对的人数是答对1题人数的3倍少6人,答对两题的人数是答对1题人数的2倍;乙班的答题情况为:没有同学全部答错,答对一题人数的3倍和答对2题的人数之和等于全部答对的人数.
①求甲班全部答对的人数;
②请判断甲乙两班哪个班的得分更高,并说明理由.
19.(2022·浙江金华·七年级期末)为更好地营造“多读书、读好书、好读书”的书香校园氛围,学校图书馆向出版商邮购某系列图书.相关的书价折扣、邮费如下表所示.(注:总费用=总书价+总邮费)
数量 折扣 邮费
不超过10本 九折 7元
超过10本 八五折 优惠后总书价的10%
(1)已知书的单价为15元,需购书30本.
①若采用分次邮购,每次10本,共需总费用为 元;
②若采用一次性邮购,共需费用为 元.
(2)已知图书馆需购书的总数是10的整数倍,且超过10本.图书馆负责人发现分次邮购所需费用与一次性邮购所需费用相同,求书的单价是多少元?
20.(2022·浙江宁波·七年级期末)如图,在数轴上点O是原点,点A表示数,点B在点A的右侧,且.
(1)点B表示的数是______.
(2)若动点P从点A出发以2个单位/秒的速度沿着x轴正方向运动,当时,求点P运动的时间.
21.(2022·浙江金华·七年级期末)如图,数轴上点A,B分别表示数-6,12,C为AB中点.
(1)求点C表示的数.
(2)若点P为线段AB上一点,PC=2,求点P表示的数.
(3)若点D为线段AB上一点,在线段AB上有两个动点M,N,分别同时从点A,D出发,沿数轴正方向运动,点M的速度为4个单位每秒,点N的速度为3个单位每秒,当MN=1,NC=2时,求点D表示的数.
22.(2022·浙江丽水·七年级期末)甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,定价相同,乒乓球拍60元/副,乒乓球20元/盒,两家商店的优惠方案如下表所示:
商店 优惠方案
甲商店 每买一副球拍赠一盒乒乓球
乙商店 全部按定价的8折优惠
某班现需买球拍5副,乒乓球若干盒(不少于5盒).
(1)当购买乒乓球8盒时,请通过计算说明去哪家商店购买更合算?
(2)当购买乒乓球多少盒时,在甲、乙两店所需支付的费用相同?
(3)若该班有500元的购买经费,请你帮忙设计出最佳的购买方案,使购买到的乒乓球的盒数最多.
23.(2022·浙江宁波·七年级期末)“水是生命之源”,某自来水公司为鼓励用户节约用水,对 “一户一表” 居民用水按以下规定收取水费:
月用水量/吨 单价(元/吨)
不超过10吨的部分 2.6
超过10吨但不超过18吨的部分 3.5
超过 18 吨的部分 4.3
注意:另外每吨用水加收 元的城市污水处理费
例如:某用户 11 月份用水 16 吨,共需交纳水费为:
元.
请根据以上信息,回答下列问题:
(1)若小聪家 11 月份用水 12 吨,那么共需交纳水费多少元
(2)若小明家 11 月份共交纳水费 元, 那么小明家 11 月份用水多少吨
(3)若小聪和小明家 12 月份共用水 23 吨,共交纳水费 元,其中小聪家用水量少于 10 吨,那么小聪家和小明家 12 月份各用水多少吨
24.(2022·浙江宁波·七年级期末)为了平衡电力负荷,减少用电高峰时段用电和不必要的能源消耗,浙江省居民生活用电可申请“峰谷电”,两种收费标准如下:
未申请峰谷电即阶梯电价收员标准:
月用电总量 (单位:千瓦时) 电度电价 (单位:元/千瓦时)
230 及以下部分
超过230至400部分
超过400部分
峰谷电收费标准:
高峰电价 低谷电价
元/千瓦时 元/千瓦时
月用电总量超过230千瓦时至400千瓦时 部分加收元/千瓦时; 月用电总登超过 400千瓦时部分加收元/千瓦时
如:某用户月用电总量300千瓦时,其中高峰时用电100千瓦时, 低谷时用电200千瓦时.如果不申请峰谷电则需费用;若申请峰谷电则需费用 .
(1)小明家5月份用电总量为400千瓦时,其中峰时用电量为150千瓦时,低谷时间段用电量为250千瓦时,如不申请峰谷电,应付电费______元;若申请峰谷电,应付电费______元;
(2)小强家未申请峰谷电,8月份一共交电费元,求小强家8月份的用电总量;
(3)小强听小朋介绍峰谷电节能且收费便宜,于是9月份就申请了峰谷电, 9月份用电总量是330千瓦时,经计算申请峰谷电后比申请前节约了元,求小强家9月份的峰时用电量为多少
25.(2022·浙江丽水·七年级期末)如图,将1,2,3,…,40这40个数按照下表进行排列,现用一个Z字框(图中阴影部分)框住表中的4个数,移动该框,设框中最小的数为.
(1)请用含的代数式表示框中4个数的和.
(2)框中4个数的和可能是132吗?若能,请求出最小的数.
26.(2022·浙江舟山·七年级期末)下表是某网约车公司的专车计价规则
计费项目 起租价 里程费 时长费
单价 10元 2.5元/千米 1元/分
注:应付车费=起租价+里程费+时长费,其中起租价10元含5千米里程费和10分钟时长费.
例如:若坐专车行驶里程为12千米,行车时间为20分钟,则需付车费:
(元).
若坐专车行驶里程为4千米,行车时间为12分钟,则需付车费:(元).
(1)若小聪乘坐专车,行车里程为20千米,行车时间为30分,则需付车费_______元;
(2)若小聪乘坐专车,行车里程为()千米,平均时速为40千米/时,则小聪应付车费多少元?(用含的代数式表示)
(3)小聪与小明各自乘坐专车从家去吾悦广场,由于堵车,小聪乘坐了12分钟,小明乘坐了20分钟,两车车费之和为47元,里程之和为15千米(其中小聪的行车里程不超过5千米).那么这两辆专车此次的行驶路程各为多少千米?
27.(2022·浙江嘉兴·七年级期末)庆祝建党100周年,学校七、八年级开展“追寻建党足迹,传承红船精神”的革命纪念馆研学活动.根据防控要求,入馆前需体温检测.其中A通道是电子测温,B通道是人工测温,A通道每分钟通过的人数是B通道的2倍.已知该校七、八年级学生人数分别为96人和144人,七年级学生进馆时,同时开通了A、B两通道,经过4分钟,学生全部进馆.
(1)分别求A、B两通道每分钟通过的人数.
(2)八年级学生进馆时,先同时开通A、B两通道,1分钟后增开一个人工测温通道C,已知C通道每分钟通过的人数是B通道的,求八年级学生全部进馆所需时间.
28.(2022·浙江湖州·七年级期末)如图,数轴上的点从左往右依次A,B,C对应的数分别为a,b,c,且|a+3|+|b-6|=0,AB的距离比BC的距离大4,动点P从点A出发沿数轴以每秒6个单位的速度向右运动,同时动点Q从点B出发沿数轴以每秒2个单位的速度一直向右运动,当点P运动到点C之后立即以原速沿数轴一直向左运动,设运动的时间为t秒.
(1)填空:a= ,b= ,点Q在数轴上所表示的数为 (用含t的代数式表示).
(2)当动点P从点A运动到点C过程中,Q点是PC的中点时,则点Q在数轴上所表示的数是多少?
(3)在整个运动过程中,是否存在t使得QB=2PC,若存在,求出t的值,若不存在,请说明理由.
29.(2022·浙江金华·七年级期末)如图,自行车每节链条的长度为2.3cm,交叉重叠部分的圆的直径为0.7cm.
(1)2节链条长 cm,5节链条长 cm,n节链条长 cm;
(2)如果一辆自行车的链条的总长度为99.9cm,求这辆自行车上有几节链条?
30.(2022·浙江宁波·七年级期末)对于数轴上给定的两点M,N(M在N的左侧),若数轴上存在点P,使得,则称点P为点M,N的“k和点”.例如,如图1,点M,N表示的数分别为0,2,点P表示的数为1,因为,所以点P是点M,N的“4和点”.
(1)如图2,已知点A表示的数为,点B表示的数为2.
①若点O表示的数为0,点O为点A,B的“k和点”,则k的值______.
②若点C在线段AB上,且点C是点A,B的“5和点”,则点C表示的数为______.
③若点D是点A,B的“k和点”,且,求k的值.
(2)数轴上点E表示的数为a,点F在点E的右侧,,点T是点E,F的“6和点”,请求出点T表示的数t的值(用含a的代数式表示).
参考答案:
1.A
【解析】设快马x天可以追上慢马,则慢马跑了(x+12)天,根据路程=速度×时间结合两匹马跑过的路程相等,即可得出关于x的一元一次方程,此题得解.
设快马x天可以追上慢马,则慢马跑了(x+12)天,
依题意,得:240x=150(x+12).
故选:A.
本题考查了一元一次方程的应用,正确理解题意,找到等量关系并列出方程是关键.
2.C
【解析】根据题意,首先计算得甲、乙两运动员每次相遇的时间间隔为:,设两人相週的次数为,根据一元一次方程的性质列方程并求解,即可得到答案.
根据题意,甲、乙两运动员每次相遇的时间间隔为:
设两人相遇的次数为
∵起跑后时间总共为2分钟,即120 s
∴
∴
根据题意,两人相遇的次数为整数
∴,即两人相遇的次数为5次
故选:C.
本题考查了一元一次方程的知识;解题的关键是熟练掌握一元一次方程的性质,从而完成求解.
3.C
【解析】此题等量关系为:2×螺钉总数=螺母总数,据此设未知数列出方程即可.
解:设安排x名工人生产螺钉,则(26-x)人生产螺母,由题意得
1000(26-x)=2×800x,
故C答案正确
故选C
4.D
【解析】设这种商品的定价是x元.根据定价的7.5折出售将赔35元和定价的9.5折出售将赚25元,分别表示出进价,从而列方程求解.
解:设这种商品的定价是x元.
根据题意,得75%x+35=95%x-25.
故选:D.
本题考查了由实际问题抽象出一元一次方程的知识,解题的关键是根据题意找到等量关系,这是列方程的关键.
5.A
【解析】设他第一天读x个字,根据题意列出方程解答即可.
解:设他第一天读x个字,根据题意可得:x+2x+4x=34685,
故选A.
此题考查由实际问题抽象出一元一次方程,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程.
6.A
【解析】根据题意求出“九宫格”中的y,再求出x即可求解.
如图,依题意可得2+5+8=2+7+y
解得y=6
∴8+x+6=2+5+8
解得x=1
故选A.
此题主要考查一元一次方程的应用,解题的关键是根据题意得到方程求解.
7.C
【解析】根据题意列出一元一次方程,即可求解.
依题意得5+4+9=5+3+a
解得a=10
故选C.
此题主要考查一元一次方程的应用,解题的关键是根据题意列出方程即可求解.
8.D
【解析】观察所给数字,利用正方形中四个数字之间的关系总结出规律,即可求解.
解:观察题目所给数字可得:第n个正方形中,左上角的数字为n,左下角的数字为,右上角的数字为,右下角的数字为左下角、右上角两个数字的积,再加上左上角的数字.
∴为第a个正方形,,
解得:,
∴,
∴,
故选D.
本题属于数字规律题,考查了列代数式、一元一次方程的应用,能够利用正方形中四个数字之间的关系总结出规律是解题的关键.
9.A
【解析】由AB的长度结合A、B表示的数互为相反数,即可得出A,B表示的数
解:∵
∴,两点对应的数互为相反数,
∴可设表示的数为,则表示的数为,
∵
∴,
解得:,
∴点表示的数为-3,
故选:A.
本题考查了绝对值,相反数的应用,关键是能根据题意得出方程.
10.C
【解析】根据各点在数轴上的位置,把b、c、d都用含a的式子表示出来,根据a和d互为相反数求出a的值,再求出b+3c的值即可.
解:由图可知:b=a+3,c=a+4,d=a+7,
∵a和d互为相反数,
∴a+d=0,即a+a+7=0,
∴a= 3.5,
∴b+3c=a+3+3(a+4)=4a+15=1.
故选:C.
本题考查了数轴,结合图形找出a、b、c、d之间的数量关系是解题的关键.
11.A
【解析】根据题意直接列方程即可.
解:根据题意,得:10x+3(5-x)=30,
故选:A.
本题考查一元一次方程的应用,理解题意,正确列出方程是解答的关键.
12.八
【解析】打折销售后要保证打折后利率为20%,因而可以得到不等关系为:利润率=20%,设可以打x折,根据不等关系列出不等式求解即可.
解:设应打x折,
则根据题意得:(180×x×10%-120)÷120=20%,
解得:x=8.
故商店应打八折.
故答案为:八.
本题考查一元一次方程的实际应用,解题关键是读懂题意,找到符合题意的等量关系式,同时要注意掌握利润率的计算方法.
13.
【解析】设羊价为x钱,根据题意可得合伙的人数为或,由合伙人数不变可得方程.
解:设羊价为x钱,
根据题意可得方程:,
故答案为:.
本题考查由实际问题抽象出一元一次方程,解答本题的关键是明确题意,找到等量关系,列出相应的方程.
14.3200或3000##3000或3200
【解析】设获一、 二、 三等奖的人数分别为a、b、c,根据①中题设求得a、b、c,再设每个三等奖的奖金额是x元,则每个一等奖的奖金额是6x,每个二等奖的奖金额是2x,根据题意列出方程求解即可.
解:设获一、 二、 三等奖的人数分别为a、b、c,
由题意,得:a+b+c=8,且0<a<b<c,a、b、c均为正整数,
∴a=1,b=2,c=5或a=1,b=3,c=4,
设每个三等奖的奖金额是x元,则每个一等奖的奖金额是6x,每个二等奖的奖金额是2x,
根据题意,得:6x+2×2x+5x=48000或6x+3×2x+4x=48000,
解得:x=3200或x=3000,
答:每个三等奖的奖金额应是3200元或3000元,
故答案为:3200或3000.
本题考查一元一次方程的应用,理解题意,正确列出方程并求得a、b、c的值是解答的关键.
15.3(x-2)=2x+9
【解析】设车为x辆,根据人数不变,即可得出关于x的一元一次方程,此题得解.
解:设车有x辆,则人有3(x-2)人,
依题意,得:3(x-2)=2x+9.
故答案为:3(x-2)=2x+9.
本题考查了一元一次方程的应用以及数学常识,找准等量关系,正确列出一元一次方程是解题的关键.
16.(1)2.5
(2)①20km;②小李追上小王的时刻为4:48.
【解析】(1)先求出小王和小李在15分钟内的路程,然后求得两个间的距离;
(2)①先设A、B两地相距x千米,然后分别用含有x的式子表示两人从A地到B地的时间,再结合“汽车比公交车早10.5分钟到达”列出方程求解,即可得到A、B两地间的距离;
②先由①得到每两个站点间的距离,然后计算得到公交车在每两个站点间的时间,进而初步判断8分钟后公交车的位置,然后设时间为m分钟,再分段进行讨论即可.
(1)
解:15分钟=0.25小时,
∴小王的路程为40×0.25=10(km),
小李的路程为50×0.25=12.5(km),
∴两人间的距离为12.5﹣10=2.5(km),
故答案为:2.5.
(2)
解:①设两地距离为x千米,则小李的从A地到B地的时间为 小时,小王的时间为 小时,
∵汽车比公交车早10.5分钟到达,
∴,
解得:x=20,
∴A、B两地相距20千米.
②由①得,A、B两地相距20千米,
∵每两个站点间的距离相等,
∴每两个站点间的距离为20÷10=2(千米),
∴小王经过两个站点间的时间为2÷40=0.05小时=3分钟,
∵3+0.5+3+0.5=7<8,
∴8分钟时,公交车在P2与P3之间,
设小李经过m分钟追上小王,
当小李在P2与P3之间追上小王,即m≤2时,
,
解得:m=28(舍);
当小李在P3与P4之间追上小王,即2.5<m≤5.5时,
,
解得:m=26(舍);
当小李在P4与P5之间追上小王,即6<m≤9时,
,
解得:m=24(舍);
当小李在P5与P6之间追上小王,即9.5<m≤12.5时,
,
解得:m=22(舍);
当小李在P6与P7之间追上小王,即13<m≤16时,
,
解得:m=20(舍);
当小李在P7与P8之间追上小王,即16.5<m≤19.5时,
,
解得:m=18;
∴经过18分钟,小李追上小王,
此时的时刻为4:48.
本题考查了一元一次方程的应用,解题的关键是会利用“路程=速度×时间”进行相关时间和路程的表示和会将时间单位进行转化.
17.(1)文具店采购了文具盲盒10盒,Molly盲盒90盒;
(2)销售完这100盒盲盒,文具店共获利1480元;
(3)销售完这100个盲盒的总利润不可能恰好为1400元.
【解析】(1)设文具店分别采购文具盲盒x盒,Molly盲盒盒,利用进价乘以件数算出总采购额,列出方程求解;
(2)用售价减进价得到单件利润,乘以(1)中的件数,得出总利润;
(3)设文具店分别采购文具盲盒m盒,Molly盲盒盒,用单件利润乘以件数,令两种盲盒的利润和为1400元,列方程求解.
(1)
解:设文具店分别采购文具盲盒x盒,Molly盲盒盒,
由题意得:,
解得,
(盒),
答:文具店采购了文具盲盒10盒,Molly盲盒90盒;
(2)
(元),
答:销售完这100盒盲盒,文具店共获利1480元;
(3)
设文具店分别采购文具盲盒m盒,Molly盲盒盒,
由题意得:,
解得,
∵m为整数,
∴不合题意,
答:销售完这100个盲盒的总利润不可能恰好为1400元.
本题考查一元一次方程的应用,解题的关键是找到题目中的等量关系列出方程进行求解.
18.(1)每位同学所有可能的得分情况是-30分、-10分、10分和30分;
(2)①甲班全部答对的人数是21人;②乙班得分更高.
【解析】(1)根据竞赛的得分规则可得答案;
(2)①设甲班答对1题的有x人,根据题意列出方程,解方程可得答案;
②首先算出甲班的得分,设乙班全部答对的有a人,答对1题的有b人,答对2题的有(a-3b)人,整理可得乙班的得分,再比较可得结论.
(1)
解:若只答对1题,则不答或答错2题,得分为:1×10-2×10=-10,
若只答对2题,则不答或答错1题,得分为:2×10-1×10=10,
若只答对3题,得分为:3×10=30,
若不答或答错3题,得分为:0-3×10=-30,
答:每位同学所有可能的得分情况是-30分、-10分、10分和30分;
(2)
解:①设甲班答对1题的有x人,
由题意得,2+(3x-6)+2x+x=50,
解得x=9,
3×9-6=21(人),
答:甲班全部答对的人数是21人;
②乙班得分更高.
由题意得,甲班答对3题有21人,答对2题的有18人,答对1题的有9人,全部答错的有2人,
故甲班的得分为21×30+18×10-9×10-2×30=660(分),
设乙班全部答对的有a人,答对1题的有b人,答对2题的有(a-3b)人,
所以a+b+(a-3b)=50,
即a-b=25,
故乙班得分为30a+10(a-3b)-10b=40(a-b)=1000(分),
1000>660,
答:乙班得分更高.
本题考查了一元一次方程的实际运用,整式加减的应用,找到等量关系列出方程是解决问题的关键.
19.(1)①426;②420.75
(2)书的单价是20元
【解析】(1)①根据表格中不超过10本的方案,可以解答本题;②根据表格中超过10本的方案,可以解答本题;
(2)设书的单价为x元,购书数量10a本(a是大于1的正整数),根据题意两种方案的费用一样建立等式求解即可.
(1)
解:①若采用分次邮购,每次10本,
根据题意有:(元),
②若采用一次性邮购,则
(元),
故答案为:426,420.75;
(2)
解:设书的单价为x元,购书数量10a本(a是大于1的正整数),根据题意得:
,
即:,
解得:x=20,
答:书的单价是20元.
本题考查一元一次方程的应用,解题的关键是明确题意,列出相应的方程求解即可.
20.(1)10
(2)3.5秒或8.5秒
【解析】(1)根据数轴上两点间的距离列式计算;
(2)设点P运动时间为t秒,然后利用数轴上两点间距离公式及OB=2BP列方程求解.
(1)
解:∵点A表示数 2,点B在点A的右侧,且AB=12,
∴ 2+12=10,
∴点B表示的数为10,
故答案为:10;
(2)
解:设点P运动时间为t秒,则在运动过程中点P所表示的数为 2+2t,
∴BP=|10 ( 2+2t)|=|12 2t|,
由题意,可得:10=2|12 2t|,
解得:t=3.5或t=8.5,
故当OB=2BP时,点P运动的时间为3.5秒或8.5秒.
本题考查了一元一次方程的应用,理解数轴上两点间距离结合方程思想解题是关键.
21.(1)3
(2)5或1
(3)-3.5或-2.5
【解析】(1)设点C表示的数为x,根据点C为AB中点,列出方程求解即可;
(2)设点P表示的数为m,根据两点间距离公式可列方程求解即可;
(3)分点N在点C的左侧和右侧两种情况讨论求解即可.
(1)
设点C表示的数为x,
∵点A表示的数为-6,点B表示的数为12,且点C为AB的中点
∴
解得,
所以,点C表示的数为:3;
(2)
设点P表示的数为m,
∵点C表示的数为3,且PC=2
∴
解得,或
∴点P表示的数为:5或1;
(3)
分两种情况:
①当点N在点C左侧时,如图,
∵,且点C表示的数为3
∴此时点N表示的数为:3-2=1
又MN=1
∴M表示的数为:1-1=0
∴
∴点M运动的时间为秒,
∴点N的运动时间也为1.5秒
∴个单位,
∴点D表示的数为:1-4.5=-3.5;
②当点N在点C的右侧时,如图,
∵,且点C表示的数为3
∴此时点N表示的数为:3+2=5
又MN=1
∴M表示的数为:5-1=4
∴
∴点M运动的时间为秒,
∴点N的运动时间也为2.5秒
∴个单位,
∴点D表示的数为:5-7.5=-2.5;
综上,点D表示的数为:-3.5或-2.5
本题考查一次方程应用及数轴上点表示的数,解题的关键是找准等量关系,正确列出一元一次方程.
22.(1)去甲商店购买更合算
(2)10盒
(3)在甲商店购买5副球拍获赠5盒乒乓球,再在乙商店购买12盒乒乓球.
【解析】(1)利用总价=单价×数量,结合两家商店给出的优惠方案,即可分别求出去甲、乙两商店购买所需费用,比较后即可得出结论;
(2)设当购买乒乓球x盒时,在甲、乙两店所需支付的费用相同,利用总价=单价×数量,结合两家商店给出的优惠方案及在两家商店购买所需费用相同,即可得出关于x的一元一次方程,解之即可得出结论;
(3)由甲、乙两家商店的优惠方案可得出最佳的购买方案为:在甲商店购买5副球拍获赠5盒乒乓球,再在乙商店购买12盒乒乓球.
(1)
解:去甲商店购买所需费用为60×5+20×(8-5)=360(元);
去乙商店购买所需费用为(60×5+20×8)×80%=368(元).
∵360<368,
∴去甲商店购买更合算.
(2)
解:设当购买乒乓球x盒时,在甲、乙两店所需支付的费用相同,
依题意得:60×5+20(x-5)=(60×5+20x)×80%,
解得:x=10.
(3)
解:甲店购买5副球拍时赠送5盒乒乓球,再次购买乒乓球需要按原价购买,而乙商店所有商品均按定价的8折优惠,
∴在甲商店购买5副球拍,赠送5盒乒乓球,剩余的钱再取乙商店购买乒乓球.
(500-60×5)÷(20×80%)=200÷16=12.5(盒).
∴最佳的购买方案为:在甲商店购买5副球拍获赠5盒乒乓球,再在乙商店购买12盒乒乓球.
本题考查了一元一次方程的应用以及有理数的混合运算,解题的关键是:(1)利用总价=单价×数量,结合两家商店给出的优惠方案,分别求出在甲、乙两家商店购买所需费用;(2)找准等量关系,正确列出一元一次方程;(3)根据两家商店给出的优惠方案,找出最佳的购买方案.
23.(1)共需交纳水费42.6元
(2)小明家 11 月份用水17吨
(3)小聪家12 月份用水9吨,小明家 12 月份用水14吨
【解析】(1)根据收费标准列式计算即可;
(2)设小明家11月份用水x吨,先判断x<18,再列方程求解;
(3)设12月份小聪家用水y吨,则小明家用水(23-y)吨,且y<10,分两种情况:当0
解:需交纳水费(元);
(2)
解:设小明家11月份用水x吨,
∵>64.1,
∴x<18,
∴,
解得x=17,
答:小明家 11 月份用水17吨;
(3)
解:设12月份小聪家用水y吨,则小明家用水(23-y)吨,且y<10,
当0
,解得(舍去);
当时,10<23-y18,
,解得y=9,
∴23-9=14
答:小聪家12 月份用水9吨,小明家 12 月份用水14吨.
此题考查了分段收费问题的一元一次方程的实际应用,正确理解各段的收费标准列出方程是解题的关键.
24.(1)224.5 ;166.5
(2)小强家8月份用电总量500千瓦时
(3)小强家9月份峰时用电100千瓦时
【解析】(1)根据两种计费方式进行求解即可;
(2)可设小强家8月份用电总量为x千瓦时,根据未申请峰谷电的方式进行列方程计算即可;
(3)根据两种方式相差54.5元可列出方程求解.
(1)解:不申请峰谷电,应付电费为:0.54×230+0.59×(400﹣230)=224.5(元),请峰谷电,应付电费为:0.57×150+0.29×250+0.05×(400﹣230)=166.5(元),故答案为:224.5,166.5;
(2)解:∵308.5>224.5,∴用电量超过400千瓦时,设小强家8月份用电总量为x千瓦时,依题意得:0.54×230+0.59×(400﹣230)+0.84(x﹣400)=308.5,解得:x=500,答:小强家8月份用电总量为500千瓦时;
(3)解:设小强家9月份的峰时用电量为y千瓦时,依题意得:0.54×230+0.59×(330﹣230)﹣[0.57y+0.29(330﹣y)+0.05×(330﹣230)]=54.5,解得:y=100,答:小强家9月份的峰时用电量为100千瓦时.
本题主要考查一元一次方程的应用,解答的关键是理解清楚题意找到等量关系.
25.(1)4x+24
(2)能,最小的数为27
【解析】(1)若框中最小的一个数为x,则其它四个数分别是x+1、x+11、x+12.然后求和即可;
(2)根据所给的数的和列方程计算,如果结果不是整数,则应舍去.
(1)
解:设框中最小的数为x,则
x+x+1+x+11+x+12=4x+24;
∴框中4个数的和为x+24.
(2)
解:根据题意,得4x+24=132.
解得x=27.
观察表格中的数据知,x=27符合题意.
答:能,最小的数是27.
此题考查了一元一次方程的应用,列代数式和数字的变化规律,关键是根据所给的数的和列方程计算解答.
26.(1)67.5;(2);(3)小聪乘坐4千米,小明乘坐11千米
【解析】(1)按收费标准计算应付车费=起租价+15千米里程费+20分钟时长费即可;
(2)先计算是否收时长费,应付车费=起租价+(x-5)千米里程费+长费化简即可;
(3)设小聪乘坐(x<5)千米,则小明乘坐千米,先求出每人的费用小聪乘坐(x<5)千米费用是起租价+时长费=10+1×(12-10)元,小明乘坐千米费用是起租价+里程费+时长费=10+2.5×(15-x-5)+1×(20-10)元,利用费用之和47构造方程,解方程即可.
解:(1)10+(20-5)×2.5+(30-10)×1,
=,
(元),
故答案为:67,5;
(2)∵,所以时间超过10分钟,
∴;
(3)设小聪乘坐(x<5)千米,则小明乘坐千米,
小聪乘坐(x<5)千米费用是起租价+时长费=10+1×(12-10)元,
小明乘坐千米费用是起租价+里程费+时长费=10+2.5×(15-x-5)+1×(20-10)元,
根据题意,得:
,
整理的2.5x=10,
解得,
∴(千米),
答:小聪乘坐4千米,小明乘坐11千米.
本题考查网约车计费列代数式与简单方程,掌握计费种类与标准,以及计费公式,利用路程之和15千米设元,利用费用之和47构造方程是解题关键.
27.(1)A通道每分钟通过16人,B通道每分钟道过8人
(2)八年级学生全部进馆需5分钟
【解析】(1)设B通道每分钟通过x人,根据题意列一元一次方程解方程求解即可;
(2)设八年级学生全部进馆需y分钟,根据题意列一元一次方程解方程求解即可;
(1)
解:设B通道每分钟通过x人,根据题意得:
,解得,则
答:A通道每分钟通过16人,B通道每分钟道过8人.
(2)
解:设八年级学生全部进馆需y分钟,根据题意得:
,解得
答:八年级学生全部进馆需5分钟.
本题考查了一元一次方程的应用,根据题意列出一元一次方程是解题的关键.
28.(1)-3,6,6+2t
(2)点Q在数轴上所表示的数是10
(3)存在,当时,;当时,
【解析】(1)根据绝对值的非负性可求出a、b的值,利用求出Q点运动的距离,再加上B所表示的数,即可求解;
(2)根据题意,,则,解方程即可求出Q为PC中点时间t,再代入即可求解;
(3),根据题意解出方程,分情况讨论即可.
(1)
解:∵|a+3|+|b-6|=0,
∴a+3=0,b-6=0,
∴ ,
∴B表示的数为6,
∵点Q从点B出发沿数轴以每秒2个单位的速度一直向右运动,
∴ ,
∴点Q在数轴上所表示的数为 ;
(2)
由(1)知A表示的数为-3,B表示的数为6,
∴ ,
∵ ,
∴ ,且C在B的右侧,
∴C点表示的数为 ,
∴ ,
∴ ,
∵ ,
∴,
∴ ,
当 时点Q在数轴上所表示的数为;
当 时点P的运动轨迹为A向C再向A,故舍去,
故当Q为PC中点时,Q所表示的数为10;
(3)
,
当时,即 ,
∴ ,
P到达C点时 ,
∴当时,P点由A向C运动,
即 时, ,
当,P点由A向C再向A运动,
即时, .
本题主要考查了一元一次方程的应用,数轴和绝对值,解题的关键是读懂题意,找到等量关系,列出方程并解答,难度较大.
29.(1)3.9;8.7;1.6n+0.7
(2)62
【解析】(1)根据题目中链条的结构及计算规律即可得出结果;
(2)将链条长度等于99.9cm代入(1)中解析式中求解即可得.
(1)
解:根据图形可得出:
2节链条的长度为:
2.3×2-0.7=3.9cm,
3节链条的长度为:
2.3×3-0.7×2=5.5cm,
4节链条的长度为:
2.3×4-0.7×3=7.1cm,
5节链条的长度为:
2.3×5-0.7×4=8.7cm,
…
n节链条的长度为:
2.3×n-0.7×(n-1)=1.6n+0.7cm,
故答案为:3.9;8.7;1.6n+0.7;
(2)
解:由题意得:1.6n+0.7=99.9,
解得:n=62,
答:这辆自行车有62节链条.
本题主要考查规律探索及解一元一次方程,理解题意,找出相应规律是解题关键.
30.(1)①8;②1.5;③或20
(2)t的值为或
【解析】(1)①根据定义得OA+3OB=k,计算即可;
②设点C表示的数为c,根据题意列方程求解;
③分两种情况:当点D在AB之间,点D位于点B右侧,求出AD、BD,根据公式即可求出k;
(2)分三种情况:①当点T位于点E左侧,②当点T在线段EF上时,③当点T位于点F右侧,列方程解答 .
(1)
解:①∵点O为点A,B的“k和点”,
∴OA+3OB=k,
∴点A表示的数为,点B表示的数为2.
∴OA=2,OB=2,
∴k=8,
故答案为:8;
②设点C表示的数为c,
∵点C是点A,B的“5和点”,
∴AC+3BC=5,
∴c+2+3(2-c)=5,
解得c=1.5,
故答案为:1.5;
③当点D在AB之间,
∵,
∴,,
∴;
点D位于点B右侧,
∵,
∴,
∴,
∴.
故k的值为或20;
(2)
解:①当点T位于点E左侧,即时,显然不满足条件.
②当点T在线段EF上时,
∵,
∴.
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴.
③当点T位于点F右侧时,
∵,
∴,
又∵点T是点E,F的“6和点”,
∴,
∴,,
∴,
综上所述,t的值为或.
此题考查了数轴上两点之间的距离,一元一次方程的实际应用,解题中运用分类思想解决问题是解题的关键.
