2021-2022学年浙江省各地人教版数学八年级上册11.2 与三角形有关的角 期末试题分类选编(含解析)
文档属性
| 名称 | 2021-2022学年浙江省各地人教版数学八年级上册11.2 与三角形有关的角 期末试题分类选编(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 466.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-16 07:31:51 | ||
图片预览


文档简介
11.2 与三角形有关的角
1.(2022··八年级期末)将一副三角板按如图所示的方式放置,则∠α的度数为( )
A.65° B.75° C.85° D.95°
2.(2022·浙江丽水·八年级期末)在△ABC中,∠A=60°,∠B=50°,则∠C的度数为( )
A.60° B.30° C.70° D.50°
3.(2022·浙江金华·八年级期末)如图,点A,B,C分别代表王老师的家,图书馆,学校.已知图书馆B在王老师家A的北偏东32°方向上,学校C在图书馆B的北偏西32°方向上.则∠ABC的度数是( )
A.112° B.114° C.116° D.118°
4.(2022·浙江台州·八年级期末)如图,在中,,,是的平分线,于点,则的度数是( )
A. B. C. D.
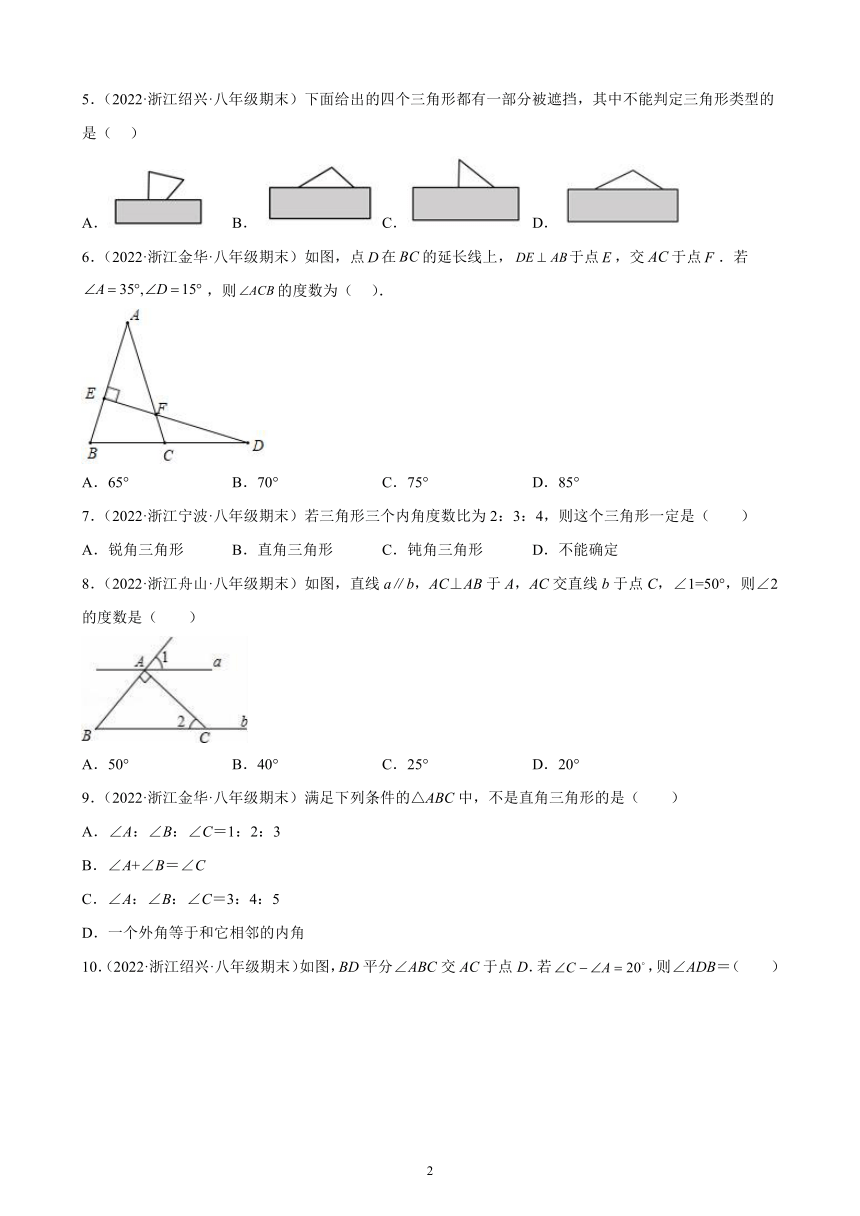
5.(2022·浙江绍兴·八年级期末)下面给出的四个三角形都有一部分被遮挡,其中不能判定三角形类型的是( )
A. B. C. D.
6.(2022·浙江金华·八年级期末)如图,点在的延长线上,于点,交于点.若,则的度数为( ).
A.65° B.70° C.75° D.85°
7.(2022·浙江宁波·八年级期末)若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
8.(2022·浙江舟山·八年级期末)如图,直线a∥b,AC⊥AB于A,AC交直线b于点C,∠1=50°,则∠2的度数是( )
A.50° B.40° C.25° D.20°
9.(2022·浙江金华·八年级期末)满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3
B.∠A+∠B=∠C
C.∠A:∠B:∠C=3:4:5
D.一个外角等于和它相邻的内角
10.(2022·浙江绍兴·八年级期末)如图,BD平分∠ABC交AC于点D.若,则∠ADB=( )
A.100° B.105° C.110° D.120°
11.(2022·浙江金华·八年级期末)如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=28°,则∠CDE=( )
A. B. C. D.
12.(2022·浙江浙江·八年级期末)如图,下列关于,,,的关系中一定成立的是( )
A. B.
C. D.
13.(2022·浙江宁波·八年级期末)在中,,,则是______三角形.(选填“锐角”、“直角”或“钝角”)
14.(2022·浙江丽水·八年级期末)三角形三个内角的和等于__________
15.(2022·浙江宁波·八年级期末)在△ABC中,若∠A=35°,∠B=65°,则∠C的度数为______.
16.(2022·浙江丽水·八年级期末)如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,∠AEC=105°,则∠B=___°.
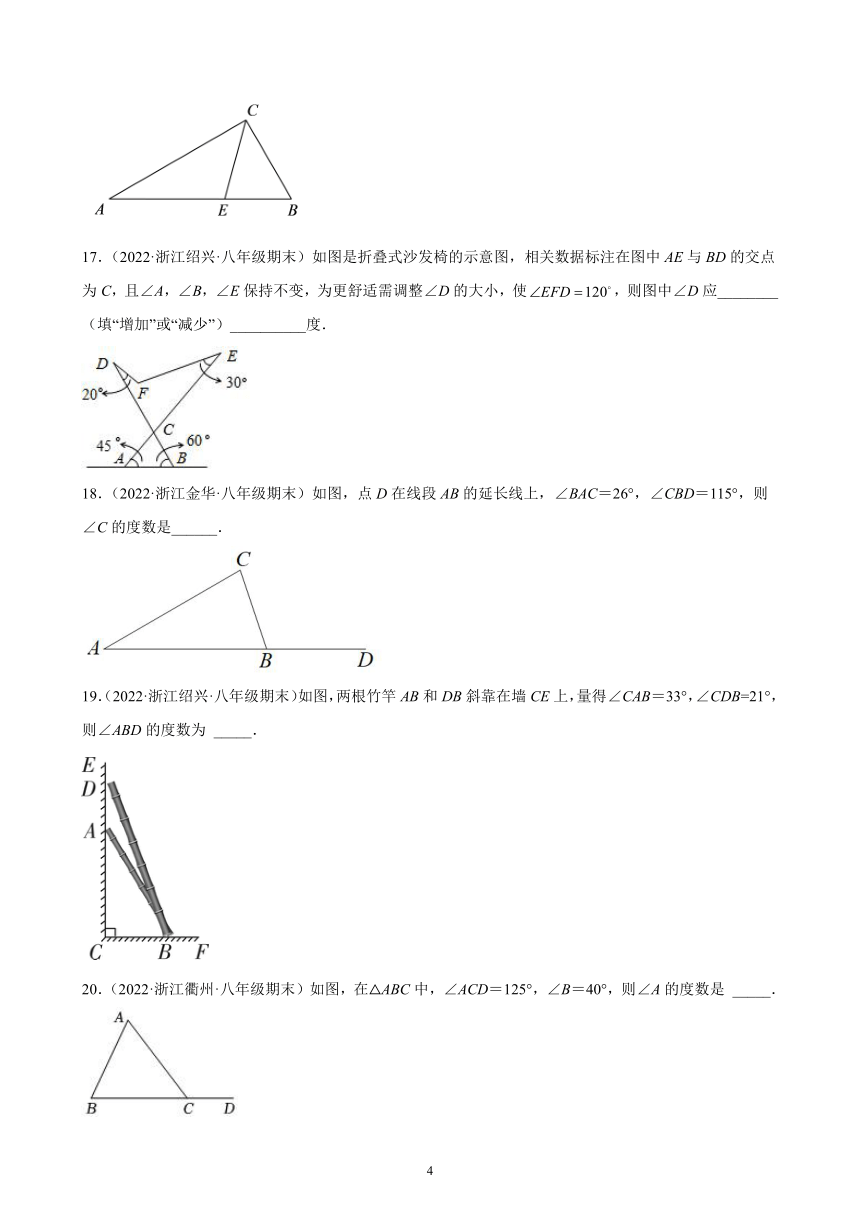
17.(2022·浙江绍兴·八年级期末)如图是折叠式沙发椅的示意图,相关数据标注在图中AE与BD的交点为C,且∠A,∠B,∠E保持不变,为更舒适需调整∠D的大小,使,则图中∠D应________(填“增加”或“减少”)__________度.
18.(2022·浙江金华·八年级期末)如图,点D在线段AB的延长线上,∠BAC=26°,∠CBD=115°,则∠C的度数是______.
19.(2022·浙江绍兴·八年级期末)如图,两根竹竿AB和DB斜靠在墙CE上,量得∠CAB=33°,∠CDB=21°,则∠ABD的度数为 _____.
20.(2022·浙江衢州·八年级期末)如图,在△ABC中,∠ACD=125°,∠B=40°,则∠A的度数是 _____.
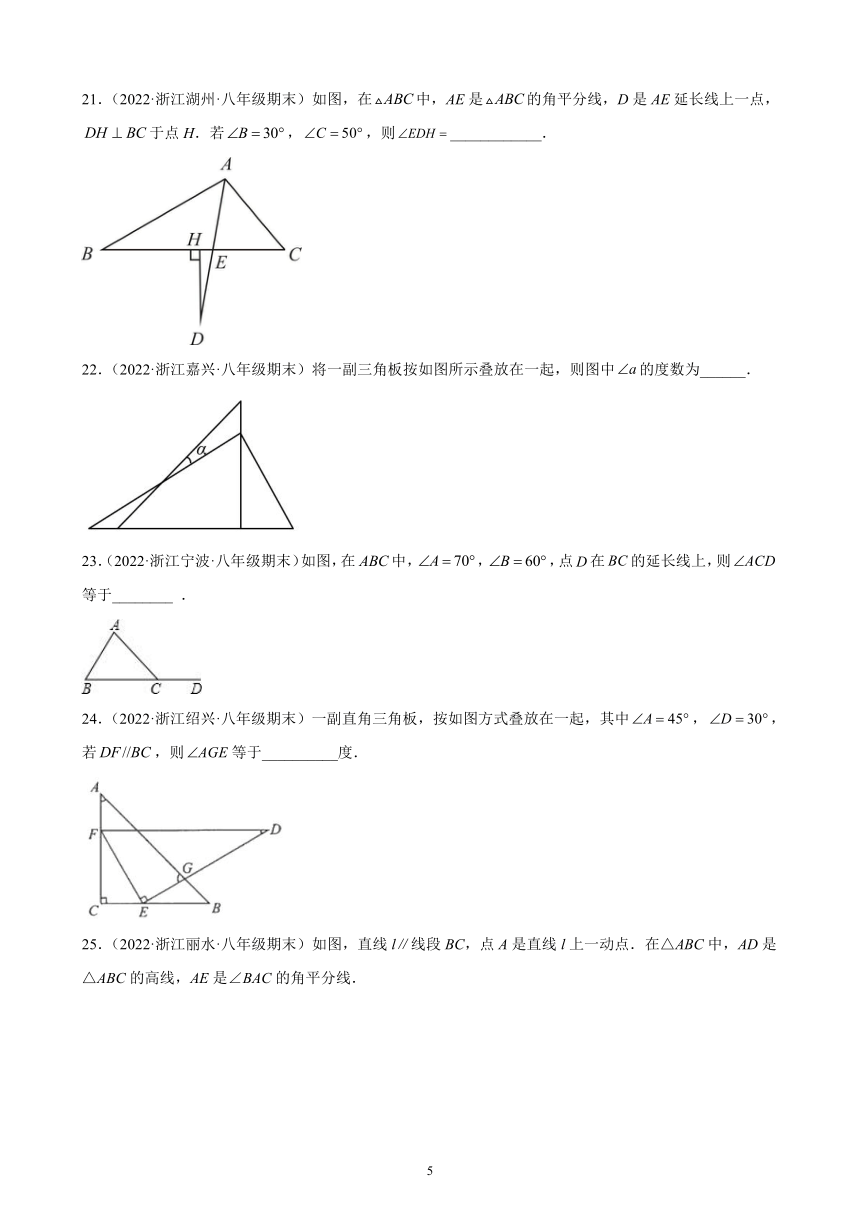
21.(2022·浙江湖州·八年级期末)如图,在中,AE是的角平分线,D是AE延长线上一点,于点H.若,,则____________.
22.(2022·浙江嘉兴·八年级期末)将一副三角板按如图所示叠放在一起,则图中的度数为______.
23.(2022·浙江宁波·八年级期末)如图,在中,,,点在的延长线上,则等于________ .
24.(2022·浙江绍兴·八年级期末)一副直角三角板,按如图方式叠放在一起,其中,,若,则等于__________度.
25.(2022·浙江丽水·八年级期末)如图,直线l∥线段BC,点A是直线l上一动点.在△ABC中,AD是△ABC的高线,AE是∠BAC的角平分线.
(1)如图1,若∠ABC=65°,∠BAC=80°,求∠DAE的度数;
(2)当点A在直线l上运动时,探究∠BAD,∠DAE,∠BAE之间的数量关系,并画出对应图形进行说明.
26.(2022·浙江绍兴·八年级期末)在探索并证明三角形的内角和定理“三角形三个内角的和等于180°”时,圆圆同学添加的辅助线为“过点A作直线DE // BC”.请写出“已知”、“求证”,并补全证明.
已知:
求证:
证明:过点A作直线DE // BC.
27.(2022·浙江湖州·八年级期末)如图,在△ABC中,AD是△ABC的高线,AE是∠BAC的角平分线,已知∠BAC=100°.
(1)若∠DAE=20°,求∠C的度数;
(2)设∠DAE=(),用含有的代数式表示∠C的大小.
28.(2022·浙江杭州·八年级期末)在探索并证明三角形的内角和定理“三角形三个内角的和等于180°”时,圆圆同学添加的辅助线为“过点作直线DEBC”.请写出“已知”、“求证”,并补全证明.
已知:DEBC.求证:三角形三个内角的和等于180°.
证明:过点作直线DEBC.
参考答案:
1.B
【解析】根据题意得出,,即可根据三角形内角和定理得出,根据对顶角的性质即可求出∠α的度数.
解:∵,,
∴,
∵,
∴,
故选B.
本题考查了求三角板中的角度问题,包括三角形内角和定理,对顶角性质,熟练掌握三角形内角和定理,对顶角性质是本题的关键.
2.C
【解析】根据三角形内角和定理计算即可.
解:∵,
∴ ,
故选:C.
本题考查了三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.
3.C
【解析】过点A作ADBE交BC于点D,BE方向为正北方向,根据平行线的性质求得,进而根据三角形内角和定理即可求解.
如图,过点A作ADBE交BC于点D,BE方向为正北方向,
根据题意可得,
,
,
∴,
故选C.
本题考查了方位角,三角形内角和定理,掌握三角形内角和定理是解题的关键.
4.A
【解析】根据∠DCH=∠DCB-∠HCB,利用三角形内角和定理及角平分线的定义求出∠DCB,∠HCB即可.
∵∠ACB=180°-∠A-∠B=180°-60°-70°=50°,
又∵CD平分∠ACB,
∴∠DCB=∠ACB=×50°=25°,
∵CH⊥AB,
∴∠CHB=90°,
∴∠HCB=90°-70°=20°,
∴∠DCH=∠DCB-∠HCB=25°-20°=5°.
故选:A.
本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.C
【解析】根据三角形的分类:直角三角形、锐角三角形、钝角三角形进行判断即可.
解:A、知道两个角,可以计算出第三个角的度数,因此可以判断出三角形类型;
B、露出的角是钝角,因此是钝角三角形;
C、露出的角是锐角,其他两角都不知道,因此不能判断出三角形类型;
D、露出的角是钝角,因此是钝角三角形;
故选:C.
此题主要考查了三角形,关键是掌握三角形的分类.
6.B
【解析】根据题意于点,交于点,则,即
解:∵
∴,
∴.
故选B.
本题考查垂直的性质,解题关键在于在证明
7.A
【解析】根据三角形内角和等于180°和已知的内角度数比即可解答.
已知内角度数比为2:3:4,根据三角形内角和等于180°可以算出三个角分别为40°,60°,80°,所以为锐角三角形.
掌握三角形内角和为180°,并且根据内角比例算出相应度数是解答本题的关键.
8.B
【解析】根据平行线的性质,由a∥b可得∠B=50°,然后根据垂直的定义得∠BAC=90°,然后根据直角三角形的两锐角互余,可求∠2.
∵a∥b,∠1=50°,
∴∠B =∠1=50°,
∵AC⊥AB
∴∠BAC=90°
∴∠2=90°-50°=40°
故选B.
9.C
【解析】依据三角形内角和以及外角的定义逐项判断△ABC的内角中是否存在90°的角即可.
A项,设∠A度数为x,则根据∠A:∠B:∠C=1:2:3可得∠B=2x,∠C=3x,根据三角形内角和为180°,可得x+2x+3x=180°,解得x=30°,则∠C=3x=90°,即△ABC是直角三角形,A项不符合题意;
B项,∵∠A+∠B+∠C=180°,∠A+∠B=∠C,∴2∠C=180°,即∠C=90°,即△ABC是直角三角形,B项不符合题意;
C项,设∠A度数为3x,则根据∠A:∠B:∠C=3:4:5可得∠B=4x,∠C=5x,根据三角形内角和为180°,可得3x+4x+5x=180°,解得x=15°,则最大的角∠C=5x=75°,即△ABC不是直角三角形,C项符合题意;
D项,三角形的一个外角与其相邻的内角相等,又可知这两个角互为邻补角,根据领补角的定义可知这两个角的和为180°,则有此外角与其相邻的内角均为90°,即△ABC是直角三角形,D项不符合题意;
故选:C.
本题考查了三角形的内角和定理以及三角形的外角性质等知识,灵活运用三角形内角和为180°是解答本题的关键.
10.A
【解析】根据角平分线性质,可得,结合三角形内角和定理与外角定理即可.
解:∵BD平分∠ABC交AC于点D,
∴,
∵即,
又∵,
∴,
∵,
即,
∴,
∴,
∴.
故选:A.
此题主要考查了三角形角平分线,解题关键是熟练运用三角形内角和定理与外角定理.
11.A
【解析】先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+28°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论.
解:∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=∠B+28°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵∠B=∠C,∠ADE=∠AED,
∴∠C+∠EDC=∠ADC-∠EDC=∠B+28°-∠EDC,
解得∠EDC=14°.
故选:A.
本题考查的是三角形外角的性质,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.
12.C
【解析】延长AD交BC于点E,利用三角形外角的性质可得∠1=∠A+∠B+∠C,进而可求解.
解:如图,延长AD交BC于点E,
∵∠AEC=∠A+∠B,∠1=∠C+∠ACE,
∴∠1=∠A+∠B+∠C,
故选:C.
本题考查三角形的外角,掌握三角形外角的性质是解题的关键.
13.直角
【解析】计算出∠C的度数,根据三角形的最大内角即可判断三角形的形状.
∵∠C=180°-∠A-∠B=90°
∴△ABC是直角三角形
故答案为:直角.
本题考查了三角形内角和定理,掌握此定理是关键.
14.180°
【解析】略
15.80°
【解析】根据三角形内角和定理得出∠C的度数.
解:∵△ABC中,∠A=35°,∠B=65°,
∴∠C=180°-35°-65°=80°;
故答案为80°.
本题主要考查了三角形内角和定理的运用,解题时注意:三角形内角和是180°.
16.60
【解析】先根据角平分线的定义求出∠BCE的度数,再利用三角形外角的性质即可求出∠B的度数.
解:∵CE平分∠ACB,∠ACB=90°,
∴,
∵∠AEC=105°,
∴∠B=∠AEC-∠BCE=60°,
故答案为:60.
本题主要考查了角平分线的定义,三角形外角的性质,正确求出∠BCE的度数是解题的关键.
17. 减少 5
【解析】延长EF交CD于点G,依据三角形的内角和定理可求∠ACB,根据对顶角相等可得∠DCE,再由三角形内角和定理的推论得到∠DGF的度数;利用∠EFD=120°,和三角形的外角的性质可得∠D的度数,从而得出结论.
解:如图,延长EF交BD于点G,
∵∠A=45°,∠B=60°,
∴∠ACB=180°-45°-60°=75°,
∴∠ECD=∠ACB=75°,
∵∠DGF=∠DCE+∠E,
∴∠DGF=75°+30°=105°.
∵∠EFD=120°,∠EFD=∠DGF+∠D,
∴∠D=15°.
∵图中∠D=20°,
∴∠D应减少5°.
故答案为:减少,5.
本题主要考查了三角形的外角的性质,三角形的内角和定理.熟练使用上述定理是解题的关键.
18.##89度
【解析】根据三角形的外角的性质即可求解.
解:∵点D在线段AB的延长线上,∠BAC=26°,∠CBD=115°,
∴,
故答案为:.
本题考查了三角形外角的定义与性质,掌握三角形的外角的性质是解题的关键.
19.12°##12度
【解析】根据三角形的外角的性质可得,得到答案.
解:∵∠CAB是△ABD的外角,∠CAB=33°,∠CDB=21°,
则,
∴∠ABD=∠CAB﹣∠CDB=12°,
故答案为:12°.
本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
20.85°##85度
【解析】直接利用三角形的外角性质进行求解即可.
解:∵∠ACD是△ABC的外角,∠ACD=125°,∠B=40°,
∴∠A=∠ACD-∠B=85°,
故答案为:85°.
本题主要考查三角形的外角性质,解答的关键是熟记三角形的外角性质并灵活运用.
21.10°
【解析】在△EFD中,由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,所以∠B+∠BAC+∠EDH=90°;联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EDH=(∠C-∠B).
解:由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,
故∠B+∠BAC+∠EDH=90° ①,
△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°,
即:∠C+∠B+∠BAC=90° ②,
②-①,得:∠EDH=(∠C-∠B)=×(50°-30°)=10°.
故答案为:10°.
本题考查三角形内角和定理、三角形的外角性质以及角平分线的定义等知识,解题的关键是证明∠EFD=(∠C-∠B).
22.15°##15度
【解析】根据三角板各内角的度数和三角形外角的性质求解即可.
解:由一副三角板按如图所示叠放在一起可知,
∠2=45°,∠1=30°,
∴∠3=∠2-∠1=15°,
∴;
故答案为:15°.
本题考查了三角形外角的性质,解题关键是明确三角板各内角的度数,熟练运用外角的性质解题.
23.130°
【解析】根据三角形的一个外角等于和它不相邻的两个内角和可得.
解:∵∠ACD是△ABC的外角,∠A=70°,∠B=60°,
∴∠ACD=∠A+∠B=70°+60°=130°.
故答案为;130°.
本题考查的是三角形外角的性质,即三角形的一个外角等于和它不相邻的两个内角的和.
24.75.
【解析】根据和均是直角三角形,其中,,可得,,再根据,得,利用三角形外角的性质,即可得到.
解:∵和均是直角三角形,其中,,
∴,,
∵,,
∴,
∴,
∴,
故答案是:75.
本题考查了直角三角形的性质,平行的性质,外角的性质,熟悉相关性质是解题的关键.
25.(1)15°
(2)见解析
【解析】(1)根据角平分线的定义得∠BAE=∠BAC=40°.而∠BAD=90° ∠ABD=25°,利用角的和差关系可得答案;
(2)根据高在形内和形外进行分类,再根据AB,AC,AD的位置进行讨论.
(1)
解:∵AE是∠BAC的角平分线,
∴∠BAE=∠BAC=40°,
∵AD是△ABC的高线,
∴∠BDA=90°,
∴∠BAD=90°-∠ABD=25°,
∴∠DAE=∠BAE-∠BAD=40°-25°=15°.
(2)
①当点D落在线段CB的延长线时,如图所示:
此时∠BAD+∠BAE=∠DAE;
②当点D在线段BC上,且在E点的左侧时,如图所示:
此时∠BAD+∠DAE=∠BAE;
③当点D在线段BC上,且在E点的右侧时,如图所示:
此时∠BAE+∠DAE=∠BAD;
④当点D在BC的延长线上时,如图所示:
∠BAE+∠DAE=∠BAD.
本题主要考查了角平分线的定义,三角形内角和定理等知识,运用分类讨论思想是解题的关键.
26.已知:如图,;求证:;证明见解析.
【解析】根据平行线的性质和平角的定义即可证明.
已知:如图,.
求证:.
证明:如图,过点A作直线DE // BC.
∵DE // BC,
∴,(两直线平行,内错角相等).
∵(平角定义),
∴.
即三角形内角和为.
本题考查三角形内角和定理的证明,平行线的性质,平角的定义.掌握两直线平行,内错角相等是解题关键.
27.(1)20°
(2)40°-α
【解析】(1)由题意可求得∠AED=70°,再由角平分线的定义可得∠EAC=50°,即可求∠C的度数;
(2)仿照(1)的解答过程进行求解即可.
(1)
解:∵在Rt△ADE中,∠DAE=20°,
∴∠AED=90°-20°=70°,
又∵∠BAC=100°,AE是角平分线,
∴∠EAC=50°,
∴∠C=∠AED-∠EAC=70°-50°=20°;
(2)
解:∵在Rt△ADE中,∠DAE=α,
∴∠AED=90°-α,
又∵∠BAC=100°,AE是角平分线,
∴∠EAC=50°,
∴∠C=∠AED-∠EAC=(90°-α)-50°=40°-α.
本题主要考查三角形的内角和定理,解题的关键是结合图形分析清楚各角之间的关系.
28.见解析
【解析】过点A作DEBC,依据平行线的性质,即可得到,,再根据平角的定义,即可得到三角形的内角和为180°.
解:已知:,,是的三个内角,
求证:.
证明:如图,过点作直线.
∴,,
∵点D,A,E在同一条直线上,
∴∠BAC+∠DAB+∠EAC=180°,
∴,
即三角形的内角和为180°.
本题主要考查了平行线的性质以及三角形内角和定理的运用,熟练掌握平行线的性质是解题的关键.
1.(2022··八年级期末)将一副三角板按如图所示的方式放置,则∠α的度数为( )
A.65° B.75° C.85° D.95°
2.(2022·浙江丽水·八年级期末)在△ABC中,∠A=60°,∠B=50°,则∠C的度数为( )
A.60° B.30° C.70° D.50°
3.(2022·浙江金华·八年级期末)如图,点A,B,C分别代表王老师的家,图书馆,学校.已知图书馆B在王老师家A的北偏东32°方向上,学校C在图书馆B的北偏西32°方向上.则∠ABC的度数是( )
A.112° B.114° C.116° D.118°
4.(2022·浙江台州·八年级期末)如图,在中,,,是的平分线,于点,则的度数是( )
A. B. C. D.
5.(2022·浙江绍兴·八年级期末)下面给出的四个三角形都有一部分被遮挡,其中不能判定三角形类型的是( )
A. B. C. D.
6.(2022·浙江金华·八年级期末)如图,点在的延长线上,于点,交于点.若,则的度数为( ).
A.65° B.70° C.75° D.85°
7.(2022·浙江宁波·八年级期末)若三角形三个内角度数比为2:3:4,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
8.(2022·浙江舟山·八年级期末)如图,直线a∥b,AC⊥AB于A,AC交直线b于点C,∠1=50°,则∠2的度数是( )
A.50° B.40° C.25° D.20°
9.(2022·浙江金华·八年级期末)满足下列条件的△ABC中,不是直角三角形的是( )
A.∠A:∠B:∠C=1:2:3
B.∠A+∠B=∠C
C.∠A:∠B:∠C=3:4:5
D.一个外角等于和它相邻的内角
10.(2022·浙江绍兴·八年级期末)如图,BD平分∠ABC交AC于点D.若,则∠ADB=( )
A.100° B.105° C.110° D.120°
11.(2022·浙江金华·八年级期末)如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=28°,则∠CDE=( )
A. B. C. D.
12.(2022·浙江浙江·八年级期末)如图,下列关于,,,的关系中一定成立的是( )
A. B.
C. D.
13.(2022·浙江宁波·八年级期末)在中,,,则是______三角形.(选填“锐角”、“直角”或“钝角”)
14.(2022·浙江丽水·八年级期末)三角形三个内角的和等于__________
15.(2022·浙江宁波·八年级期末)在△ABC中,若∠A=35°,∠B=65°,则∠C的度数为______.
16.(2022·浙江丽水·八年级期末)如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,∠AEC=105°,则∠B=___°.
17.(2022·浙江绍兴·八年级期末)如图是折叠式沙发椅的示意图,相关数据标注在图中AE与BD的交点为C,且∠A,∠B,∠E保持不变,为更舒适需调整∠D的大小,使,则图中∠D应________(填“增加”或“减少”)__________度.
18.(2022·浙江金华·八年级期末)如图,点D在线段AB的延长线上,∠BAC=26°,∠CBD=115°,则∠C的度数是______.
19.(2022·浙江绍兴·八年级期末)如图,两根竹竿AB和DB斜靠在墙CE上,量得∠CAB=33°,∠CDB=21°,则∠ABD的度数为 _____.
20.(2022·浙江衢州·八年级期末)如图,在△ABC中,∠ACD=125°,∠B=40°,则∠A的度数是 _____.
21.(2022·浙江湖州·八年级期末)如图,在中,AE是的角平分线,D是AE延长线上一点,于点H.若,,则____________.
22.(2022·浙江嘉兴·八年级期末)将一副三角板按如图所示叠放在一起,则图中的度数为______.
23.(2022·浙江宁波·八年级期末)如图,在中,,,点在的延长线上,则等于________ .
24.(2022·浙江绍兴·八年级期末)一副直角三角板,按如图方式叠放在一起,其中,,若,则等于__________度.
25.(2022·浙江丽水·八年级期末)如图,直线l∥线段BC,点A是直线l上一动点.在△ABC中,AD是△ABC的高线,AE是∠BAC的角平分线.
(1)如图1,若∠ABC=65°,∠BAC=80°,求∠DAE的度数;
(2)当点A在直线l上运动时,探究∠BAD,∠DAE,∠BAE之间的数量关系,并画出对应图形进行说明.
26.(2022·浙江绍兴·八年级期末)在探索并证明三角形的内角和定理“三角形三个内角的和等于180°”时,圆圆同学添加的辅助线为“过点A作直线DE // BC”.请写出“已知”、“求证”,并补全证明.
已知:
求证:
证明:过点A作直线DE // BC.
27.(2022·浙江湖州·八年级期末)如图,在△ABC中,AD是△ABC的高线,AE是∠BAC的角平分线,已知∠BAC=100°.
(1)若∠DAE=20°,求∠C的度数;
(2)设∠DAE=(),用含有的代数式表示∠C的大小.
28.(2022·浙江杭州·八年级期末)在探索并证明三角形的内角和定理“三角形三个内角的和等于180°”时,圆圆同学添加的辅助线为“过点作直线DEBC”.请写出“已知”、“求证”,并补全证明.
已知:DEBC.求证:三角形三个内角的和等于180°.
证明:过点作直线DEBC.
参考答案:
1.B
【解析】根据题意得出,,即可根据三角形内角和定理得出,根据对顶角的性质即可求出∠α的度数.
解:∵,,
∴,
∵,
∴,
故选B.
本题考查了求三角板中的角度问题,包括三角形内角和定理,对顶角性质,熟练掌握三角形内角和定理,对顶角性质是本题的关键.
2.C
【解析】根据三角形内角和定理计算即可.
解:∵,
∴ ,
故选:C.
本题考查了三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.
3.C
【解析】过点A作ADBE交BC于点D,BE方向为正北方向,根据平行线的性质求得,进而根据三角形内角和定理即可求解.
如图,过点A作ADBE交BC于点D,BE方向为正北方向,
根据题意可得,
,
,
∴,
故选C.
本题考查了方位角,三角形内角和定理,掌握三角形内角和定理是解题的关键.
4.A
【解析】根据∠DCH=∠DCB-∠HCB,利用三角形内角和定理及角平分线的定义求出∠DCB,∠HCB即可.
∵∠ACB=180°-∠A-∠B=180°-60°-70°=50°,
又∵CD平分∠ACB,
∴∠DCB=∠ACB=×50°=25°,
∵CH⊥AB,
∴∠CHB=90°,
∴∠HCB=90°-70°=20°,
∴∠DCH=∠DCB-∠HCB=25°-20°=5°.
故选:A.
本题考查三角形内角和定理,角平分线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
5.C
【解析】根据三角形的分类:直角三角形、锐角三角形、钝角三角形进行判断即可.
解:A、知道两个角,可以计算出第三个角的度数,因此可以判断出三角形类型;
B、露出的角是钝角,因此是钝角三角形;
C、露出的角是锐角,其他两角都不知道,因此不能判断出三角形类型;
D、露出的角是钝角,因此是钝角三角形;
故选:C.
此题主要考查了三角形,关键是掌握三角形的分类.
6.B
【解析】根据题意于点,交于点,则,即
解:∵
∴,
∴.
故选B.
本题考查垂直的性质,解题关键在于在证明
7.A
【解析】根据三角形内角和等于180°和已知的内角度数比即可解答.
已知内角度数比为2:3:4,根据三角形内角和等于180°可以算出三个角分别为40°,60°,80°,所以为锐角三角形.
掌握三角形内角和为180°,并且根据内角比例算出相应度数是解答本题的关键.
8.B
【解析】根据平行线的性质,由a∥b可得∠B=50°,然后根据垂直的定义得∠BAC=90°,然后根据直角三角形的两锐角互余,可求∠2.
∵a∥b,∠1=50°,
∴∠B =∠1=50°,
∵AC⊥AB
∴∠BAC=90°
∴∠2=90°-50°=40°
故选B.
9.C
【解析】依据三角形内角和以及外角的定义逐项判断△ABC的内角中是否存在90°的角即可.
A项,设∠A度数为x,则根据∠A:∠B:∠C=1:2:3可得∠B=2x,∠C=3x,根据三角形内角和为180°,可得x+2x+3x=180°,解得x=30°,则∠C=3x=90°,即△ABC是直角三角形,A项不符合题意;
B项,∵∠A+∠B+∠C=180°,∠A+∠B=∠C,∴2∠C=180°,即∠C=90°,即△ABC是直角三角形,B项不符合题意;
C项,设∠A度数为3x,则根据∠A:∠B:∠C=3:4:5可得∠B=4x,∠C=5x,根据三角形内角和为180°,可得3x+4x+5x=180°,解得x=15°,则最大的角∠C=5x=75°,即△ABC不是直角三角形,C项符合题意;
D项,三角形的一个外角与其相邻的内角相等,又可知这两个角互为邻补角,根据领补角的定义可知这两个角的和为180°,则有此外角与其相邻的内角均为90°,即△ABC是直角三角形,D项不符合题意;
故选:C.
本题考查了三角形的内角和定理以及三角形的外角性质等知识,灵活运用三角形内角和为180°是解答本题的关键.
10.A
【解析】根据角平分线性质,可得,结合三角形内角和定理与外角定理即可.
解:∵BD平分∠ABC交AC于点D,
∴,
∵即,
又∵,
∴,
∵,
即,
∴,
∴,
∴.
故选:A.
此题主要考查了三角形角平分线,解题关键是熟练运用三角形内角和定理与外角定理.
11.A
【解析】先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+28°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论.
解:∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=∠B+28°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵∠B=∠C,∠ADE=∠AED,
∴∠C+∠EDC=∠ADC-∠EDC=∠B+28°-∠EDC,
解得∠EDC=14°.
故选:A.
本题考查的是三角形外角的性质,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.
12.C
【解析】延长AD交BC于点E,利用三角形外角的性质可得∠1=∠A+∠B+∠C,进而可求解.
解:如图,延长AD交BC于点E,
∵∠AEC=∠A+∠B,∠1=∠C+∠ACE,
∴∠1=∠A+∠B+∠C,
故选:C.
本题考查三角形的外角,掌握三角形外角的性质是解题的关键.
13.直角
【解析】计算出∠C的度数,根据三角形的最大内角即可判断三角形的形状.
∵∠C=180°-∠A-∠B=90°
∴△ABC是直角三角形
故答案为:直角.
本题考查了三角形内角和定理,掌握此定理是关键.
14.180°
【解析】略
15.80°
【解析】根据三角形内角和定理得出∠C的度数.
解:∵△ABC中,∠A=35°,∠B=65°,
∴∠C=180°-35°-65°=80°;
故答案为80°.
本题主要考查了三角形内角和定理的运用,解题时注意:三角形内角和是180°.
16.60
【解析】先根据角平分线的定义求出∠BCE的度数,再利用三角形外角的性质即可求出∠B的度数.
解:∵CE平分∠ACB,∠ACB=90°,
∴,
∵∠AEC=105°,
∴∠B=∠AEC-∠BCE=60°,
故答案为:60.
本题主要考查了角平分线的定义,三角形外角的性质,正确求出∠BCE的度数是解题的关键.
17. 减少 5
【解析】延长EF交CD于点G,依据三角形的内角和定理可求∠ACB,根据对顶角相等可得∠DCE,再由三角形内角和定理的推论得到∠DGF的度数;利用∠EFD=120°,和三角形的外角的性质可得∠D的度数,从而得出结论.
解:如图,延长EF交BD于点G,
∵∠A=45°,∠B=60°,
∴∠ACB=180°-45°-60°=75°,
∴∠ECD=∠ACB=75°,
∵∠DGF=∠DCE+∠E,
∴∠DGF=75°+30°=105°.
∵∠EFD=120°,∠EFD=∠DGF+∠D,
∴∠D=15°.
∵图中∠D=20°,
∴∠D应减少5°.
故答案为:减少,5.
本题主要考查了三角形的外角的性质,三角形的内角和定理.熟练使用上述定理是解题的关键.
18.##89度
【解析】根据三角形的外角的性质即可求解.
解:∵点D在线段AB的延长线上,∠BAC=26°,∠CBD=115°,
∴,
故答案为:.
本题考查了三角形外角的定义与性质,掌握三角形的外角的性质是解题的关键.
19.12°##12度
【解析】根据三角形的外角的性质可得,得到答案.
解:∵∠CAB是△ABD的外角,∠CAB=33°,∠CDB=21°,
则,
∴∠ABD=∠CAB﹣∠CDB=12°,
故答案为:12°.
本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
20.85°##85度
【解析】直接利用三角形的外角性质进行求解即可.
解:∵∠ACD是△ABC的外角,∠ACD=125°,∠B=40°,
∴∠A=∠ACD-∠B=85°,
故答案为:85°.
本题主要考查三角形的外角性质,解答的关键是熟记三角形的外角性质并灵活运用.
21.10°
【解析】在△EFD中,由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,所以∠B+∠BAC+∠EDH=90°;联立△ABC中,由三角形内角和定理得到的式子,即可推出∠EDH=(∠C-∠B).
解:由三角形的外角性质知:∠HED=∠AEC=∠B+∠BAC,
故∠B+∠BAC+∠EDH=90° ①,
△ABC中,由三角形内角和定理得:
∠B+∠BAC+∠C=180°,
即:∠C+∠B+∠BAC=90° ②,
②-①,得:∠EDH=(∠C-∠B)=×(50°-30°)=10°.
故答案为:10°.
本题考查三角形内角和定理、三角形的外角性质以及角平分线的定义等知识,解题的关键是证明∠EFD=(∠C-∠B).
22.15°##15度
【解析】根据三角板各内角的度数和三角形外角的性质求解即可.
解:由一副三角板按如图所示叠放在一起可知,
∠2=45°,∠1=30°,
∴∠3=∠2-∠1=15°,
∴;
故答案为:15°.
本题考查了三角形外角的性质,解题关键是明确三角板各内角的度数,熟练运用外角的性质解题.
23.130°
【解析】根据三角形的一个外角等于和它不相邻的两个内角和可得.
解:∵∠ACD是△ABC的外角,∠A=70°,∠B=60°,
∴∠ACD=∠A+∠B=70°+60°=130°.
故答案为;130°.
本题考查的是三角形外角的性质,即三角形的一个外角等于和它不相邻的两个内角的和.
24.75.
【解析】根据和均是直角三角形,其中,,可得,,再根据,得,利用三角形外角的性质,即可得到.
解:∵和均是直角三角形,其中,,
∴,,
∵,,
∴,
∴,
∴,
故答案是:75.
本题考查了直角三角形的性质,平行的性质,外角的性质,熟悉相关性质是解题的关键.
25.(1)15°
(2)见解析
【解析】(1)根据角平分线的定义得∠BAE=∠BAC=40°.而∠BAD=90° ∠ABD=25°,利用角的和差关系可得答案;
(2)根据高在形内和形外进行分类,再根据AB,AC,AD的位置进行讨论.
(1)
解:∵AE是∠BAC的角平分线,
∴∠BAE=∠BAC=40°,
∵AD是△ABC的高线,
∴∠BDA=90°,
∴∠BAD=90°-∠ABD=25°,
∴∠DAE=∠BAE-∠BAD=40°-25°=15°.
(2)
①当点D落在线段CB的延长线时,如图所示:
此时∠BAD+∠BAE=∠DAE;
②当点D在线段BC上,且在E点的左侧时,如图所示:
此时∠BAD+∠DAE=∠BAE;
③当点D在线段BC上,且在E点的右侧时,如图所示:
此时∠BAE+∠DAE=∠BAD;
④当点D在BC的延长线上时,如图所示:
∠BAE+∠DAE=∠BAD.
本题主要考查了角平分线的定义,三角形内角和定理等知识,运用分类讨论思想是解题的关键.
26.已知:如图,;求证:;证明见解析.
【解析】根据平行线的性质和平角的定义即可证明.
已知:如图,.
求证:.
证明:如图,过点A作直线DE // BC.
∵DE // BC,
∴,(两直线平行,内错角相等).
∵(平角定义),
∴.
即三角形内角和为.
本题考查三角形内角和定理的证明,平行线的性质,平角的定义.掌握两直线平行,内错角相等是解题关键.
27.(1)20°
(2)40°-α
【解析】(1)由题意可求得∠AED=70°,再由角平分线的定义可得∠EAC=50°,即可求∠C的度数;
(2)仿照(1)的解答过程进行求解即可.
(1)
解:∵在Rt△ADE中,∠DAE=20°,
∴∠AED=90°-20°=70°,
又∵∠BAC=100°,AE是角平分线,
∴∠EAC=50°,
∴∠C=∠AED-∠EAC=70°-50°=20°;
(2)
解:∵在Rt△ADE中,∠DAE=α,
∴∠AED=90°-α,
又∵∠BAC=100°,AE是角平分线,
∴∠EAC=50°,
∴∠C=∠AED-∠EAC=(90°-α)-50°=40°-α.
本题主要考查三角形的内角和定理,解题的关键是结合图形分析清楚各角之间的关系.
28.见解析
【解析】过点A作DEBC,依据平行线的性质,即可得到,,再根据平角的定义,即可得到三角形的内角和为180°.
解:已知:,,是的三个内角,
求证:.
证明:如图,过点作直线.
∴,,
∵点D,A,E在同一条直线上,
∴∠BAC+∠DAB+∠EAC=180°,
∴,
即三角形的内角和为180°.
本题主要考查了平行线的性质以及三角形内角和定理的运用,熟练掌握平行线的性质是解题的关键.
