2021-2022学年浙江省各地人教版数学八年级上册13.1 轴对称 期末试题分类选编(含解析)
文档属性
| 名称 | 2021-2022学年浙江省各地人教版数学八年级上册13.1 轴对称 期末试题分类选编(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 587.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-16 00:00:00 | ||
图片预览




文档简介
13.1 轴对称
1.(2022·浙江舟山·八年级期末)如图,下列图案是我国几家银行的标志,其中轴对称的图形有( )
A.1个 B.2个 C.3个 D.4个
2.(2022·浙江·杭州外国语学校八年级期末)如图图形是以科学家名字命名的,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.(2022·浙江宁波·八年级期末)下列选项中的图标,属于轴对称图形的是( )
A. B. C. D.
4.(2022·浙江宁波·八年级期末)下列图标中,可以看作是轴对称图形的是( )
A. B. C. D.
5.(2022·浙江丽水·八年级期末)下列垃圾分类图标中,是轴对称图形的是( )
A. B. C. D.
6.(2022·浙江金华·八年级期末)下列图标中,是轴对称图的是( )
A. B. C. D.
7.(2022·浙江绍兴·八年级期末)篆体是我国古代汉字书体之一.下列篆体字“复”,“兴”,“之”,“路”中,是轴对称图形的为( ).
A. B. C. D.
8.(2022·浙江绍兴·八年级期末)下列图案中,属于轴对称图形的是( )
A. B. C. D.
9.(2022·浙江宁波·八年级期末)下列四个数学符号中,是轴对称图形的是( )
A. B. C. D.
10.(2022·浙江嘉兴·八年级期末)如图,折叠直角三角形纸片ABC,使得点A,B都与斜边AB上的点F重合,折痕分别为DE和GH,则下列结论不一定成立的是( )
A. B. C. D.
11.(2022·浙江宁波·八年级期末)如图,在四边形中,,将沿翻折,得到.若,则的度数为( )
A. B. C. D.
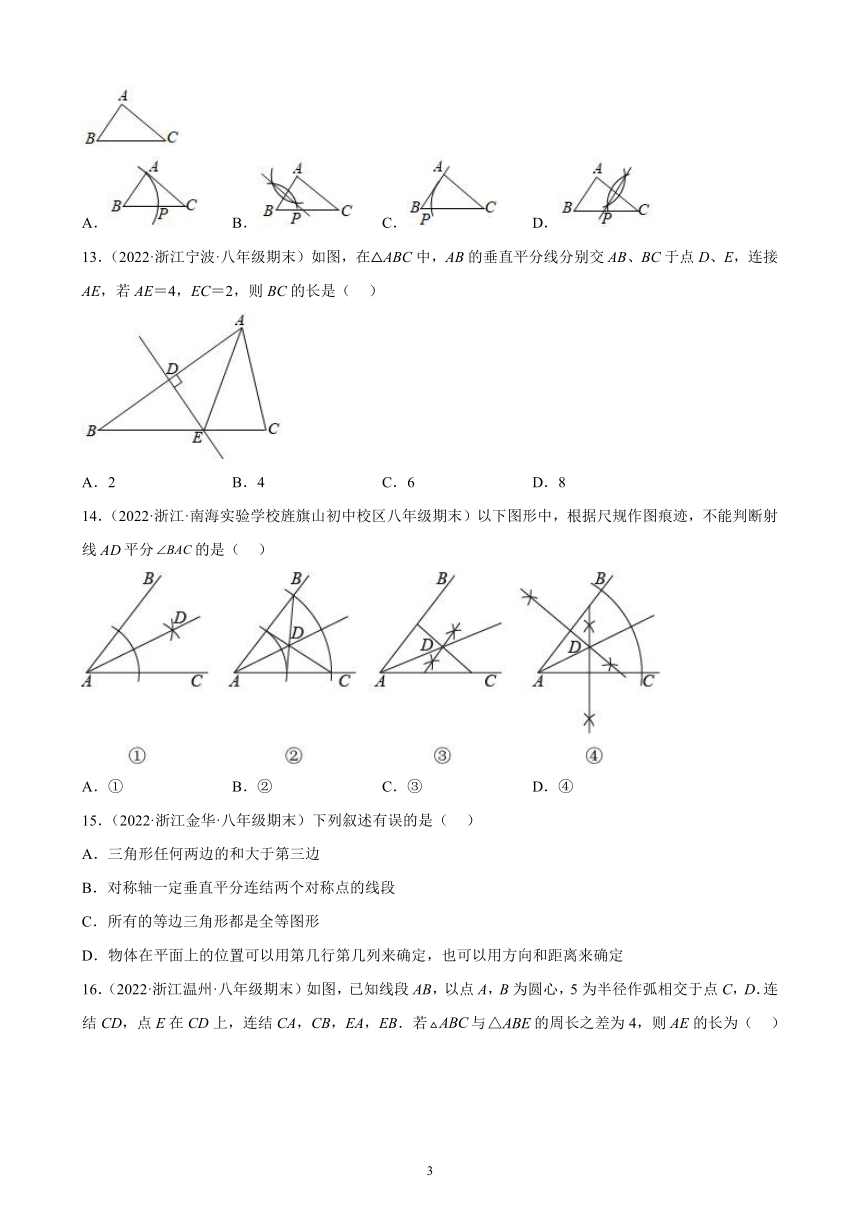
12.(2022·浙江湖州·八年级期末)如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A. B. C. D.
13.(2022·浙江宁波·八年级期末)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2 B.4 C.6 D.8
14.(2022·浙江·南海实验学校旌旗山初中校区八年级期末)以下图形中,根据尺规作图痕迹,不能判断射线平分的是( )
A.① B.② C.③ D.④
15.(2022·浙江金华·八年级期末)下列叙述有误的是( )
A.三角形任何两边的和大于第三边
B.对称轴一定垂直平分连结两个对称点的线段
C.所有的等边三角形都是全等图形
D.物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定
16.(2022·浙江温州·八年级期末)如图,已知线段AB,以点A,B为圆心,5为半径作弧相交于点C,D.连结CD,点E在CD上,连结CA,CB,EA,EB.若与的周长之差为4,则AE的长为( )
A.1 B.2 C.3 D.4
17.(2022·浙江绍兴·八年级期末)下列尺规作图分别表示:①作一个角的平分线,②作一条线段的垂直平分线.其中作法正确的是( )
A.① B.② C.①② D.无
18.(2022·浙江丽水·八年级期末)如图,在△ABC中,AB=AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧相交于点E、F,直线EF交BC于点D.连接AD,已知AC=4,△ABD的周长是10,则BC的长是( )
A.5 B.6 C.7 D.8
19.(2022·浙江宁波·八年级期末)下列命题的逆命题是假命题的是( )
A.两直线平行,同位角相等 B.线段垂直平分线上的点到线段两端距离相等
C.对顶角相等 D.等腰三角形两腰上的高线相等
20.(2022·浙江浙江·八年级期末)如图,在中,直线是边的垂直平分线,连接,若,则的周长为_________.
21.(2022·浙江绍兴·八年级期末)如图,在平行四边形中,,以点为圆心,长为半径画弧交于点,再分别以点,为圆心,大于的长为半径画弧,两弧交于一点,连接并延长交于点,连接.设与相交于点,若四边形的周长为16,则四边形的面积是_________.
22.(2022·浙江杭州·八年级期末)“等腰三角形底边上的高线与中线互相重合”的逆命题是______.这个逆命题是______命题.(真、假)
23.(2022·浙江宁波·八年级期末)如图,△ABC(∠B>∠A).
(1)在边AC上用尺规作图作出点D,使∠CDB=2∠A(保留作图痕迹);
(2)在(1)的情况下,连接BD,若CB=CD,∠A=35°,求∠C的度数.
24.(2022·浙江台州·八年级期末)如图,两条公路,相交于点,在内部有两个村庄,.为方便群众接种新冠疫苗,该地决定在内部再启动一个方舱式接种点,要求同时满足:
(1)到两条公路,的距离相等.
(2)到两村庄,的距离相等.请你用直尺和圆规作出接种点的位置(保留作图痕迹).
25.(2022·浙江·金华市第五中学八年级期末)如图,已知△ABC,其中AB=AC.作AC的垂直平分线DE,交AC于点D,交AB于点E,连结CE(尺规作图,不写作法,保留作图痕迹);
在(1)所作的图中.若BC=7.AC=9.求△BCE的周长.
参考答案:
1.C
【解析】根据轴对称图形的概念对各图形分析判断后即可得解.
解:图1不是轴对称图形;
图2是轴对称图形;
图3是轴对称图形;
图4是轴对称图形;
∴轴对称图形的共3个.
故选:C.
本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,本题仔细观察图形是解题的关键.
2.B
【解析】解:“笛卡尔心形线”和“科克曲线”是轴对称图形,共有2个,
故选:B.
本题考查了轴对称图形,熟记轴对称图形的定义(如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形)是解题关键.
3.A
【解析】直接根据轴对称图形的概念进行判断即可;
A、是轴对称图形,故A符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、不是轴对称图形,故D不符合题意;
故选:A.
本题考查了轴对称图形的识别,正确掌握知识点是解题的关键;
4.B
【解析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:A.不是轴对称图形,故此选项不合题意;
B.是轴对称图形,故此选项符合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意;
故选:B.
此题主要考查了轴对称图形,关键是掌握轴对称图形的定义.
5.D
【解析】根据轴对称图形的概念对各选项分析判断即可得解.
解:A、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
本题考查了轴对称图形的概念,识别轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
6.D
【解析】根据轴对称图形的概念求解即可.
A.不是轴对称图形,故A错误,不符合题意;
B.不是轴对称图形,故B错误,不符合题意;
C.不是轴对称图形,故C错误,不符合题意;
D.是轴对称图形,故D正确,符合题意.
故选:D.
本题考查了轴对称图形的概念.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
7.B
【解析】根据轴对称图形的定义进行判断即可.
由轴对称图形的定义:将一个图形沿某条直线折叠后,直线两旁的部分能完全重合的图形是轴对称图形,可知A、C、D不是轴对称图形,B是轴对称图形.
故选:B.
本题考查了轴对称图形的判断,重点在于熟练掌握轴对称图形的概念.
8.C
【解析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,根据轴对称图形的概念求解.
解:A、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、是轴对称图形,故本选项符合题意;
D、不是轴对称图形,故本选项不合题意.
故选:C.
本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
9.B
【解析】根据轴对称图形的定义:轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,即可判定.
A选项,不符合轴对称图形的定义,错误;
B选项,符合轴对称图形的定义,正确;
C选项,不符合轴对称图形的定义,错误;
D选项,不符合轴对称图形的定义,错误;
故选:B
此题主要考查对轴对称图形的判定,熟练掌握轴对称图形的定义,即可解题.
10.B
【解析】由折叠的性质得△ADE≌△FDE,△BHG≌△FHG,根据全等三角形的性质逐一判断即可.
解:根据折叠的性质得:△ADE≌△FDE,△BHG≌△FHG,
∴AD=FD=AF,BH=FH=BF,∠ADE=∠FDE= 90°,∠BHG=∠FHG= 90°,
∠A=∠DFE,∠B=∠HFG,
∴DH=FD+FH=(AF+BF)=AB,故选项A正确,不符合题意;
∵△ABC是直角三角形,
∴∠A+∠B= 90°,
∴∠EFG=180°-(∠DFE+∠HFG) =180°-(∠A+∠B) = 90°,
即EF⊥FG,故选项C正确,不符合题意;
∵∠FDE= 90°,∠FHG= 90°,
∴DE∥GH,故选项D正确,不符合题意;
EF与FG不一定相等,故选项B不正确,符合题意;
故选:B.
本题考查了折叠的性质,三角形内角和定理等知识,熟记各图形的性质并准确识图是解题的关键.
11.C
【解析】首先利用平行线的性质得出∠BME=120°,∠ENB=70°,再利用翻折变换的性质得出∠FMN=∠BMN=60°,∠FNM=∠MNB=35°,进而求出∠B的度数即可得出∠D的度数.
解:∵,∠A=120°,∠C=70°,
∴∠BME=120°,∠ENB=70°,
∵将△BMN沿MN翻折得△EMN,
∴∠EMN=∠BMN=60°,∠ENM=∠MNB=35°,
∴∠E=∠B=180°-60°-35°=85°,
∴∠D=360°-120°-70°-85°=85°,
故选:C.
此题主要考查了平行线的性质以及多边形内角和定理以及翻折变换的性质,得出∠EMN=∠BMN,∠ENM=∠MNB是解题关键.
12.B
解:∵PB+PC=BC,PA+PC=BC,
∴PA=PB,
根据线段垂直平分线定理的逆定理可得,点P在线段AB的垂直平分线上,
故可判断B选项正确.
故选B.
13.C
【解析】根据线段的垂直平分线的性质得到EB=EA=4,结合图形计算,得到答案.
解:∵DE是AB的垂直平分线,AE=4,
∴EB=EA=4,
∴BC=EB+EC=4+2=6,
故选:C.
本题考查的是线段的垂直平分线的性质,解题的关键是掌握线段的垂直平分线上的点到线段的两个端点的距离相等.
14.C
【解析】根据角平分线的作法以及全等三角形的判定和性质逐一进行判断即可.
图①中,利用基本作图可判断AD平分∠BAC;
在图②中,根据作法可知:
AE=AF,AM=AN,
在△AMF和△ANE中,,
∴△AMF≌△ANE(SAS),
∴∠AMD=∠AND,
∵∠MDE=∠NDF,
∵AE=AF,AM=AN,
∴ME=NF,
在△MDE和△NDF中,,
∴△MDE≌△NDF(AAS),
所以D点到AM和AN的距离相等,
∴AD平分∠BAC;
在图③中,利用基本作图得到D点为GH的中点,则不能判定AD平分∠BAC;
在图④中,根据作法可知:
AD=DB,AD=DC,AB=AC,
∴AD=DB=DC,
又AD=AD,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD,
∴AD平分∠BAC;
综上,只有图③不能判定AD平分∠BAC,
故选:C.
本题考查了作图-基本作图,角平分线的性质,线段垂直平分线的性质,全等三角形的判定与性质,解决本题的关键是掌握角平分线的作法.
15.C
【解析】根据构成三角形三边关系的条件,垂直平分线的性质,相似三角形的判定,物体的位置的确定等,依次判断即可得出结果.
解:A、三角形任何两边的和大于第三边,正确;
B、对称轴一定垂直平分连结两个对称点的线段,正确;
C、所有的等边三角形不一定全等,选项错误;
D、物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定,正确;
故选:C.
题目主要考查构成三角形三边关系的条件,垂直平分线的性质,相似三角形的判定,物体的位置的确定等,熟练掌握运用这些知识点是解题关键.
16.C
【解析】根据作图的意义,可得CD是线段AB的垂直平分线,与的周长之差为4,就是2AC-2AE=4,AC=5,代入计算即可.
根据作图的意义,可得CD是线段AB的垂直平分线,
∴与的周长之差为4,就是2AC-2AE=4,
∴AC=5,
∴10-2AE=4,
解得AE=3,
故选C.
本题考查了线段的垂直平分线的基本作图,正确理解作图的意义,并灵活计算是解题的关键.
17.A
【解析】利用作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线的作法进而判断即可得出答案.
解:①作一个角的平分线的作法正确;
②作一条线段的垂直平分线,缺少另一个交点,故作法错误;
故选:A.
本题主要考查了基本作图,正确把握作图方法是解题关键.
18.B
【解析】由线段垂直平分线的性质得到AD=CD,再根据△ABD的周长为10,推出AC+CD+BD=10,由此即可得到答案.
解:由作图方法可知直线EF是线段AC的垂直平分线,
∴AD=CD,
∵△ABD的周长为10,
∴AB+AD+BD=10,
∵AC=AB,AD=CD,
∴AC+CD+BD=10,
∴CD+BD=10-AC=6,即BC=6,
故选B.
本题主要考查了线段垂直平分线的性质,线段垂直平分线的尺规作图,熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键.
19.C
【解析】根据对顶角相等,垂直平分线的性质,平行线的性质,等腰三角形的对称性逐项分析判断即可.
解:A、两直线平行,同位角相等,逆命题为:同位角相等,两直线平行,故该选项的逆命题是真命题,不符合题意;
B. 线段垂直平分线上的点到线段两端的距离相等,逆命题为:到线段两端距离相等的点在这条线段的垂直平分线上,故该选项的逆命题是真命题,不符合题意;
C. 对顶角相等,逆命题为:若两个角相等,则这两个角是对顶角,故该选项的逆命题是假命题,符合题意;
D. 等腰三角形两腰上的高线相等,逆命题为:若三角形两条边上的高相等,则这个三角形是等腰三角形,故该选项的逆命题是真命题,不符合题意;
故选C.
本题考查了判断真假命题及写出逆命题,掌握对顶角相等,垂直平分线的性质,平行线的性质,等腰三角形的对称性是解题的关键.
20.8
【解析】根据线段垂直平分线的性质解答.
解:是边的垂直平分线,
故答案为:8.
本题考查线段垂直平分线的性质,是重要考点,掌握相关知识是解题关键.
21.
【解析】根据题意可知AE是BF的垂直平分线,可得AB=AF,BE=EF,再根据“AAS”证明△AOF≌△EOB,可得AF=BE,进而根据“四边相等的四边形是菱形”得出四边形ABEF是菱形,可知AF=AB=4,再说明△ABF是等边三角形,可求出BF=4,然后根据勾股定理求出AO,最后根据菱形的面积等于对角线乘积的一半得出答案即可.
根据题意可知AE是BF的垂直平分线,
∴AB=AF,BE=EF.
∵∠FAO=∠BEO,∠AOF=∠BOE,BO=FO,
∴△AOF≌△EOB,
∴AF=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴AF=AB=4.
∵四边形ABCD是平行四边形,且∠C=60°,
∴∠BAF=60°,
∴△ABF是等边三角形,
∴BF=4,
∴OF=2.
在Rt△AOF中,,
∴.
∴.
故答案为:.
本题主要考查了尺规作垂直平分线,菱形的判定和性质,平行四边形的性质,等边三角形的判定和性质,勾股定理等,掌握菱形面积的计算方法是解题的关键.
22. 如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形 真
【解析】将原命题的条件和结论互换,然后再写成如果……,那么……的形式就得到逆命题,然后根据垂直平分线的性质或用全等三角形的性质和判定证明即可.
给定命题的条件是:等腰三角形;结论是:底边上的高线与中线互相重合,
将条件和结论互换,写成如果……,那么……的形式得到逆命题:如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形.
这个命题是真命题,证明过程如下:
已知:如图,在三角形ABC中,AD⊥BC,D为BC的中点,
求证:AB=AC.
证明:∵AD⊥BC,D为BC的中点,
∴AD是BC的垂直平分线,
∴AB=AC,三角形ABC为等腰三角形.
故答案为:如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形;真.
本题考查了逆命题和垂直平分线的性质,学生需要熟练写出给定命题的逆命题,而且证明一个命题为真命题的步骤书写要规范.
23.(1)详见解析;(2)∠C=40°.
【解析】(1) 作AB的垂直平分线交AC于点D,则DA= DB;
(2)由(1)得∠CDB=2∠A,因为CB=CD,所以∠CBD=∠CDB,再根据三角形内角和定理即可求解.
解:(1)如图,点D为所作;
(2)由(1)得∠CDB=2∠A=2×35°=70°,
∵CB=CD,
∴∠CBD=∠CDB=70°,
∴∠C=180°﹣70°﹣70°=40°.
此题主要考查了基本作图、等腰三角形的性质以及三角形内角和定理,正确掌握线段垂直平分线的性质是解题关键.
24.见解析
【解析】作线段CD的垂直平分线和∠AOB的角平分线,其交点即为所求.
如图,作线段CD的垂直平分线MN,作∠AOB的角平分线OF,OF交MN于点P,则点P即为所求.
本题考查作图—作线段垂直平分线,作图—作角平分线,解题的关键是掌握线段垂直平分线、角平分线的性质并知道如何正确的作图.
25.(1)作图见解析;(2)16.
【解析】(1)利用线段垂直平分线的作法作图即可;
(2)首先根据等腰三角形的性质,得到AB=AC=9,再根据垂直平分线的性质可得AE=CE,进而可算出周长.
解:(1)如图所示:直线DE即为所求;
(2)∵AB=AC=9,
∵DE垂直平分AB,
∴AE=EC,
∴△BCE的周长=BC+BE+CE=BC+BE+AE=BC+AB=16.
本题主要考查了基本作图,以及线段垂直平分线的作法,等腰三角形的性质,关键是掌握线段垂直平分线的作法.
1.(2022·浙江舟山·八年级期末)如图,下列图案是我国几家银行的标志,其中轴对称的图形有( )
A.1个 B.2个 C.3个 D.4个
2.(2022·浙江·杭州外国语学校八年级期末)如图图形是以科学家名字命名的,其中是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
3.(2022·浙江宁波·八年级期末)下列选项中的图标,属于轴对称图形的是( )
A. B. C. D.
4.(2022·浙江宁波·八年级期末)下列图标中,可以看作是轴对称图形的是( )
A. B. C. D.
5.(2022·浙江丽水·八年级期末)下列垃圾分类图标中,是轴对称图形的是( )
A. B. C. D.
6.(2022·浙江金华·八年级期末)下列图标中,是轴对称图的是( )
A. B. C. D.
7.(2022·浙江绍兴·八年级期末)篆体是我国古代汉字书体之一.下列篆体字“复”,“兴”,“之”,“路”中,是轴对称图形的为( ).
A. B. C. D.
8.(2022·浙江绍兴·八年级期末)下列图案中,属于轴对称图形的是( )
A. B. C. D.
9.(2022·浙江宁波·八年级期末)下列四个数学符号中,是轴对称图形的是( )
A. B. C. D.
10.(2022·浙江嘉兴·八年级期末)如图,折叠直角三角形纸片ABC,使得点A,B都与斜边AB上的点F重合,折痕分别为DE和GH,则下列结论不一定成立的是( )
A. B. C. D.
11.(2022·浙江宁波·八年级期末)如图,在四边形中,,将沿翻折,得到.若,则的度数为( )
A. B. C. D.
12.(2022·浙江湖州·八年级期末)如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A. B. C. D.
13.(2022·浙江宁波·八年级期末)如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,连接AE,若AE=4,EC=2,则BC的长是( )
A.2 B.4 C.6 D.8
14.(2022·浙江·南海实验学校旌旗山初中校区八年级期末)以下图形中,根据尺规作图痕迹,不能判断射线平分的是( )
A.① B.② C.③ D.④
15.(2022·浙江金华·八年级期末)下列叙述有误的是( )
A.三角形任何两边的和大于第三边
B.对称轴一定垂直平分连结两个对称点的线段
C.所有的等边三角形都是全等图形
D.物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定
16.(2022·浙江温州·八年级期末)如图,已知线段AB,以点A,B为圆心,5为半径作弧相交于点C,D.连结CD,点E在CD上,连结CA,CB,EA,EB.若与的周长之差为4,则AE的长为( )
A.1 B.2 C.3 D.4
17.(2022·浙江绍兴·八年级期末)下列尺规作图分别表示:①作一个角的平分线,②作一条线段的垂直平分线.其中作法正确的是( )
A.① B.② C.①② D.无
18.(2022·浙江丽水·八年级期末)如图,在△ABC中,AB=AC,分别以点A,C为圆心,大于AC的长为半径画弧,两弧相交于点E、F,直线EF交BC于点D.连接AD,已知AC=4,△ABD的周长是10,则BC的长是( )
A.5 B.6 C.7 D.8
19.(2022·浙江宁波·八年级期末)下列命题的逆命题是假命题的是( )
A.两直线平行,同位角相等 B.线段垂直平分线上的点到线段两端距离相等
C.对顶角相等 D.等腰三角形两腰上的高线相等
20.(2022·浙江浙江·八年级期末)如图,在中,直线是边的垂直平分线,连接,若,则的周长为_________.
21.(2022·浙江绍兴·八年级期末)如图,在平行四边形中,,以点为圆心,长为半径画弧交于点,再分别以点,为圆心,大于的长为半径画弧,两弧交于一点,连接并延长交于点,连接.设与相交于点,若四边形的周长为16,则四边形的面积是_________.
22.(2022·浙江杭州·八年级期末)“等腰三角形底边上的高线与中线互相重合”的逆命题是______.这个逆命题是______命题.(真、假)
23.(2022·浙江宁波·八年级期末)如图,△ABC(∠B>∠A).
(1)在边AC上用尺规作图作出点D,使∠CDB=2∠A(保留作图痕迹);
(2)在(1)的情况下,连接BD,若CB=CD,∠A=35°,求∠C的度数.
24.(2022·浙江台州·八年级期末)如图,两条公路,相交于点,在内部有两个村庄,.为方便群众接种新冠疫苗,该地决定在内部再启动一个方舱式接种点,要求同时满足:
(1)到两条公路,的距离相等.
(2)到两村庄,的距离相等.请你用直尺和圆规作出接种点的位置(保留作图痕迹).
25.(2022·浙江·金华市第五中学八年级期末)如图,已知△ABC,其中AB=AC.作AC的垂直平分线DE,交AC于点D,交AB于点E,连结CE(尺规作图,不写作法,保留作图痕迹);
在(1)所作的图中.若BC=7.AC=9.求△BCE的周长.
参考答案:
1.C
【解析】根据轴对称图形的概念对各图形分析判断后即可得解.
解:图1不是轴对称图形;
图2是轴对称图形;
图3是轴对称图形;
图4是轴对称图形;
∴轴对称图形的共3个.
故选:C.
本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,本题仔细观察图形是解题的关键.
2.B
【解析】解:“笛卡尔心形线”和“科克曲线”是轴对称图形,共有2个,
故选:B.
本题考查了轴对称图形,熟记轴对称图形的定义(如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形)是解题关键.
3.A
【解析】直接根据轴对称图形的概念进行判断即可;
A、是轴对称图形,故A符合题意;
B、不是轴对称图形,故B不符合题意;
C、不是轴对称图形,故C不符合题意;
D、不是轴对称图形,故D不符合题意;
故选:A.
本题考查了轴对称图形的识别,正确掌握知识点是解题的关键;
4.B
【解析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:A.不是轴对称图形,故此选项不合题意;
B.是轴对称图形,故此选项符合题意;
C.不是轴对称图形,故此选项不合题意;
D.不是轴对称图形,故此选项不合题意;
故选:B.
此题主要考查了轴对称图形,关键是掌握轴对称图形的定义.
5.D
【解析】根据轴对称图形的概念对各选项分析判断即可得解.
解:A、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、是轴对称图形,故本选项符合题意.
故选:D.
本题考查了轴对称图形的概念,识别轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
6.D
【解析】根据轴对称图形的概念求解即可.
A.不是轴对称图形,故A错误,不符合题意;
B.不是轴对称图形,故B错误,不符合题意;
C.不是轴对称图形,故C错误,不符合题意;
D.是轴对称图形,故D正确,符合题意.
故选:D.
本题考查了轴对称图形的概念.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.
7.B
【解析】根据轴对称图形的定义进行判断即可.
由轴对称图形的定义:将一个图形沿某条直线折叠后,直线两旁的部分能完全重合的图形是轴对称图形,可知A、C、D不是轴对称图形,B是轴对称图形.
故选:B.
本题考查了轴对称图形的判断,重点在于熟练掌握轴对称图形的概念.
8.C
【解析】如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,根据轴对称图形的概念求解.
解:A、不是轴对称图形,故本选项不合题意;
B、不是轴对称图形,故本选项不合题意;
C、是轴对称图形,故本选项符合题意;
D、不是轴对称图形,故本选项不合题意.
故选:C.
本题考查了轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合.
9.B
【解析】根据轴对称图形的定义:轴对称图形,是指在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形,即可判定.
A选项,不符合轴对称图形的定义,错误;
B选项,符合轴对称图形的定义,正确;
C选项,不符合轴对称图形的定义,错误;
D选项,不符合轴对称图形的定义,错误;
故选:B
此题主要考查对轴对称图形的判定,熟练掌握轴对称图形的定义,即可解题.
10.B
【解析】由折叠的性质得△ADE≌△FDE,△BHG≌△FHG,根据全等三角形的性质逐一判断即可.
解:根据折叠的性质得:△ADE≌△FDE,△BHG≌△FHG,
∴AD=FD=AF,BH=FH=BF,∠ADE=∠FDE= 90°,∠BHG=∠FHG= 90°,
∠A=∠DFE,∠B=∠HFG,
∴DH=FD+FH=(AF+BF)=AB,故选项A正确,不符合题意;
∵△ABC是直角三角形,
∴∠A+∠B= 90°,
∴∠EFG=180°-(∠DFE+∠HFG) =180°-(∠A+∠B) = 90°,
即EF⊥FG,故选项C正确,不符合题意;
∵∠FDE= 90°,∠FHG= 90°,
∴DE∥GH,故选项D正确,不符合题意;
EF与FG不一定相等,故选项B不正确,符合题意;
故选:B.
本题考查了折叠的性质,三角形内角和定理等知识,熟记各图形的性质并准确识图是解题的关键.
11.C
【解析】首先利用平行线的性质得出∠BME=120°,∠ENB=70°,再利用翻折变换的性质得出∠FMN=∠BMN=60°,∠FNM=∠MNB=35°,进而求出∠B的度数即可得出∠D的度数.
解:∵,∠A=120°,∠C=70°,
∴∠BME=120°,∠ENB=70°,
∵将△BMN沿MN翻折得△EMN,
∴∠EMN=∠BMN=60°,∠ENM=∠MNB=35°,
∴∠E=∠B=180°-60°-35°=85°,
∴∠D=360°-120°-70°-85°=85°,
故选:C.
此题主要考查了平行线的性质以及多边形内角和定理以及翻折变换的性质,得出∠EMN=∠BMN,∠ENM=∠MNB是解题关键.
12.B
解:∵PB+PC=BC,PA+PC=BC,
∴PA=PB,
根据线段垂直平分线定理的逆定理可得,点P在线段AB的垂直平分线上,
故可判断B选项正确.
故选B.
13.C
【解析】根据线段的垂直平分线的性质得到EB=EA=4,结合图形计算,得到答案.
解:∵DE是AB的垂直平分线,AE=4,
∴EB=EA=4,
∴BC=EB+EC=4+2=6,
故选:C.
本题考查的是线段的垂直平分线的性质,解题的关键是掌握线段的垂直平分线上的点到线段的两个端点的距离相等.
14.C
【解析】根据角平分线的作法以及全等三角形的判定和性质逐一进行判断即可.
图①中,利用基本作图可判断AD平分∠BAC;
在图②中,根据作法可知:
AE=AF,AM=AN,
在△AMF和△ANE中,,
∴△AMF≌△ANE(SAS),
∴∠AMD=∠AND,
∵∠MDE=∠NDF,
∵AE=AF,AM=AN,
∴ME=NF,
在△MDE和△NDF中,,
∴△MDE≌△NDF(AAS),
所以D点到AM和AN的距离相等,
∴AD平分∠BAC;
在图③中,利用基本作图得到D点为GH的中点,则不能判定AD平分∠BAC;
在图④中,根据作法可知:
AD=DB,AD=DC,AB=AC,
∴AD=DB=DC,
又AD=AD,
∴△ADB≌△ADC(SSS),
∴∠BAD=∠CAD,
∴AD平分∠BAC;
综上,只有图③不能判定AD平分∠BAC,
故选:C.
本题考查了作图-基本作图,角平分线的性质,线段垂直平分线的性质,全等三角形的判定与性质,解决本题的关键是掌握角平分线的作法.
15.C
【解析】根据构成三角形三边关系的条件,垂直平分线的性质,相似三角形的判定,物体的位置的确定等,依次判断即可得出结果.
解:A、三角形任何两边的和大于第三边,正确;
B、对称轴一定垂直平分连结两个对称点的线段,正确;
C、所有的等边三角形不一定全等,选项错误;
D、物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定,正确;
故选:C.
题目主要考查构成三角形三边关系的条件,垂直平分线的性质,相似三角形的判定,物体的位置的确定等,熟练掌握运用这些知识点是解题关键.
16.C
【解析】根据作图的意义,可得CD是线段AB的垂直平分线,与的周长之差为4,就是2AC-2AE=4,AC=5,代入计算即可.
根据作图的意义,可得CD是线段AB的垂直平分线,
∴与的周长之差为4,就是2AC-2AE=4,
∴AC=5,
∴10-2AE=4,
解得AE=3,
故选C.
本题考查了线段的垂直平分线的基本作图,正确理解作图的意义,并灵活计算是解题的关键.
17.A
【解析】利用作一个角等于已知角;作一个角的平分线;作一条线段的垂直平分线的作法进而判断即可得出答案.
解:①作一个角的平分线的作法正确;
②作一条线段的垂直平分线,缺少另一个交点,故作法错误;
故选:A.
本题主要考查了基本作图,正确把握作图方法是解题关键.
18.B
【解析】由线段垂直平分线的性质得到AD=CD,再根据△ABD的周长为10,推出AC+CD+BD=10,由此即可得到答案.
解:由作图方法可知直线EF是线段AC的垂直平分线,
∴AD=CD,
∵△ABD的周长为10,
∴AB+AD+BD=10,
∵AC=AB,AD=CD,
∴AC+CD+BD=10,
∴CD+BD=10-AC=6,即BC=6,
故选B.
本题主要考查了线段垂直平分线的性质,线段垂直平分线的尺规作图,熟知线段垂直平分线上的点到线段两端的距离相等是解题的关键.
19.C
【解析】根据对顶角相等,垂直平分线的性质,平行线的性质,等腰三角形的对称性逐项分析判断即可.
解:A、两直线平行,同位角相等,逆命题为:同位角相等,两直线平行,故该选项的逆命题是真命题,不符合题意;
B. 线段垂直平分线上的点到线段两端的距离相等,逆命题为:到线段两端距离相等的点在这条线段的垂直平分线上,故该选项的逆命题是真命题,不符合题意;
C. 对顶角相等,逆命题为:若两个角相等,则这两个角是对顶角,故该选项的逆命题是假命题,符合题意;
D. 等腰三角形两腰上的高线相等,逆命题为:若三角形两条边上的高相等,则这个三角形是等腰三角形,故该选项的逆命题是真命题,不符合题意;
故选C.
本题考查了判断真假命题及写出逆命题,掌握对顶角相等,垂直平分线的性质,平行线的性质,等腰三角形的对称性是解题的关键.
20.8
【解析】根据线段垂直平分线的性质解答.
解:是边的垂直平分线,
故答案为:8.
本题考查线段垂直平分线的性质,是重要考点,掌握相关知识是解题关键.
21.
【解析】根据题意可知AE是BF的垂直平分线,可得AB=AF,BE=EF,再根据“AAS”证明△AOF≌△EOB,可得AF=BE,进而根据“四边相等的四边形是菱形”得出四边形ABEF是菱形,可知AF=AB=4,再说明△ABF是等边三角形,可求出BF=4,然后根据勾股定理求出AO,最后根据菱形的面积等于对角线乘积的一半得出答案即可.
根据题意可知AE是BF的垂直平分线,
∴AB=AF,BE=EF.
∵∠FAO=∠BEO,∠AOF=∠BOE,BO=FO,
∴△AOF≌△EOB,
∴AF=BE,
∴AB=BE=EF=AF,
∴四边形ABEF是菱形,
∴AF=AB=4.
∵四边形ABCD是平行四边形,且∠C=60°,
∴∠BAF=60°,
∴△ABF是等边三角形,
∴BF=4,
∴OF=2.
在Rt△AOF中,,
∴.
∴.
故答案为:.
本题主要考查了尺规作垂直平分线,菱形的判定和性质,平行四边形的性质,等边三角形的判定和性质,勾股定理等,掌握菱形面积的计算方法是解题的关键.
22. 如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形 真
【解析】将原命题的条件和结论互换,然后再写成如果……,那么……的形式就得到逆命题,然后根据垂直平分线的性质或用全等三角形的性质和判定证明即可.
给定命题的条件是:等腰三角形;结论是:底边上的高线与中线互相重合,
将条件和结论互换,写成如果……,那么……的形式得到逆命题:如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形.
这个命题是真命题,证明过程如下:
已知:如图,在三角形ABC中,AD⊥BC,D为BC的中点,
求证:AB=AC.
证明:∵AD⊥BC,D为BC的中点,
∴AD是BC的垂直平分线,
∴AB=AC,三角形ABC为等腰三角形.
故答案为:如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形;真.
本题考查了逆命题和垂直平分线的性质,学生需要熟练写出给定命题的逆命题,而且证明一个命题为真命题的步骤书写要规范.
23.(1)详见解析;(2)∠C=40°.
【解析】(1) 作AB的垂直平分线交AC于点D,则DA= DB;
(2)由(1)得∠CDB=2∠A,因为CB=CD,所以∠CBD=∠CDB,再根据三角形内角和定理即可求解.
解:(1)如图,点D为所作;
(2)由(1)得∠CDB=2∠A=2×35°=70°,
∵CB=CD,
∴∠CBD=∠CDB=70°,
∴∠C=180°﹣70°﹣70°=40°.
此题主要考查了基本作图、等腰三角形的性质以及三角形内角和定理,正确掌握线段垂直平分线的性质是解题关键.
24.见解析
【解析】作线段CD的垂直平分线和∠AOB的角平分线,其交点即为所求.
如图,作线段CD的垂直平分线MN,作∠AOB的角平分线OF,OF交MN于点P,则点P即为所求.
本题考查作图—作线段垂直平分线,作图—作角平分线,解题的关键是掌握线段垂直平分线、角平分线的性质并知道如何正确的作图.
25.(1)作图见解析;(2)16.
【解析】(1)利用线段垂直平分线的作法作图即可;
(2)首先根据等腰三角形的性质,得到AB=AC=9,再根据垂直平分线的性质可得AE=CE,进而可算出周长.
解:(1)如图所示:直线DE即为所求;
(2)∵AB=AC=9,
∵DE垂直平分AB,
∴AE=EC,
∴△BCE的周长=BC+BE+CE=BC+BE+AE=BC+AB=16.
本题主要考查了基本作图,以及线段垂直平分线的作法,等腰三角形的性质,关键是掌握线段垂直平分线的作法.
