14.2.1乘法公式--平方差公式
文档属性
| 名称 | 14.2.1乘法公式--平方差公式 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-13 13:09:07 | ||
图片预览








文档简介
课件20张PPT。八年级 上册14.2.1 平方差公式课件说明 我们在之前已经学习了多项式与多项式的乘法。那么,当有一些特殊的多项式与多项式相乘的式子,它们有哪些运算规律呢?让我们带着这个问题,开始进行 14.2 节的学习。14.2.1 平方差公式
课件说明学习重点
平方差公式。
学习目标
通过学习本课内容,首先学会利用平方差公式的运算性质进行有规律的运算;其次将新知识与旧知识进行类比、区别,从而掌握平方差公式的运算性质与理解数学中数形结合的思想。 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .1.探索平方差公式x2-1m2-44x2-1 问题 2 观察上面等式左边的式子,你能发现什么规律? 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .x2-1m2-44x2-1 问题 3 观察上面等式右边的式子,对比等式左边的式子,你能发现什么规律?1.探索平方差公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .x2-1m2-44x2-1 问题 4 你能用字母总结这种规律吗?(a+b)(a-b) = a2-b21.探索平方差公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .x2-1m2-44x2-1 问题 5 你能用文字语言总结这种规律吗? 两个数的和与这两个数的差的积,等于这两个数的平方差.1.探索平方差公式 平方差公式:两个数的和与这两个数的差的积,等于这两个数的平方差.(a+b)(a-b) = a2-b2 问题 6 你知道这个公式是如何推导的吗?2.理解平方差公式(a+b)(a-b)= a2-ab+ab-b2
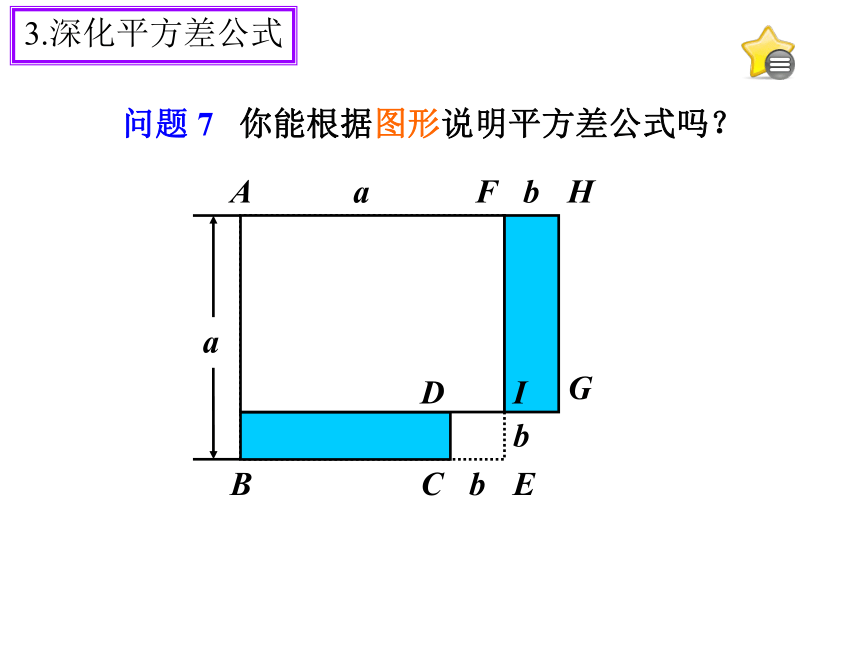
= a2-b2 问题 7 你能根据图形说明平方差公式吗?3.深化平方差公式4.巩固平方差公式例 1 计算:
(1)(3x+2)(3x-2)
(2)(-x+2y)(-x-2y)解:(1) (3x+2)(3x-2) = (3x)2-22
= 9x2-44.巩固平方差公式例 1 计算:
(1)(3x+2)(3x-2)
(2)(-x+2y)(-x-2y)解:(2) (-x+2y)(-x-2y) = (-x)2-(2y)2
= x2-4y24.巩固平方差公式练习 1 下面各式计算得对不对?如果不对,该如何改正?
(1)(2a+3b)(2a-3b) = (2a)2 -(3b)2
(2)(2a-3b)(2a-3b) = (2a)2 -(3b)2
(3)(x+2)(x-2) = x2 -2
(4)(-3a-2)(3a-2) = 9a2 -4√× 4a2-12ab+9b2× x2-4× 4-9a24.巩固平方差公式 问题 8 通过例 1 和练习 1 的练习,你知道运用平方差公式时应该注意什么?(1)在运用平方差公式,一定要看是否具备公式的特征;(2)一定要找准哪一数或式相当于公式中的 a 和公式中的 b;(3)公式中的 a 、 b 可以具体是数、单项式、多项式;(4)不能忘记公式中的“平方”.4.巩固平方差公式例 2 计算:
(1)(-y+2)(-y-2)-(y-1)(y+5)
(2)102×98解:(1)原式= y2-4-y2-4y+5
= -4y+1 (2)原式= (100+2)(100-2)
= 10000-4
= 99964.巩固平方差公式练习 2 计算:
(1)(a+3b)(a-3b)
(2)(3+2a)(-3+2a)
(3)51×49
(4)(3x+4)(3x-4)-(2x+3)(2x-3)解:(1)原式= a2-9b2(2)原式= (2a+3)(2a-3)
= (2a)2 -32
= (22)a -32
= 4a -9(3)原式= (50+1)(50-1)
= 2500-1
= 2499(4)原式= 9x2 -16-4x2 +9
= 5x2 -75.拓广平方差公式练习 3 计算:
(1)(-a+b)(a+b);
(2)(-a-b)(-a+b);
(3)(a-b)(-a-b).5.拓广平方差公式 问题 9 通过练习 3,你可以总结出平方差公式的其他形式吗? (-a+b)(a+b) = b2-a2;
(-a-b)(-a+b) = a2-b2;
(a-b)(-a-b) = b2-a2.5.拓广平方差公式练习 4 计算:
(1)(x+3)(x-3)(x2+9)
(2)20132-2012×2014解:(1)原式= (x2-9)(x2+9)
= x4 -81(2)原式= 20132-(2013-1)(2013+1)
= 20132-20132+1
= 15.拓广平方差公式例 3 观察下列等式:
① 1×3+1=22;
② 3×5+1=42;
③ 5×7+1=62.(1)从上面三个等式可以发现有什么规律? 两个连续奇数的积与 1 的和,等于夹在这两个奇数中间的偶数的平方.(2)设 2k(k 是自然数)是一个偶数,按(1)中的规律可以得等式:(2k-1)(2k+1)+1 = 4k25.拓广平方差公式例 3 观察下列等式:
① 1×3+1=22;
② 3×5+1=42;
③ 5×7+1=62.(3)如何证明 (2k-1)(2k+1)+1 = 4k2 是正确的?证明:(2k-1)(2k+1)+1
= 4k2 -1+1
= 4k2
平方差公式。
学习目标
通过学习本课内容,首先学会利用平方差公式的运算性质进行有规律的运算;其次将新知识与旧知识进行类比、区别,从而掌握平方差公式的运算性质与理解数学中数形结合的思想。 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .1.探索平方差公式x2-1m2-44x2-1 问题 2 观察上面等式左边的式子,你能发现什么规律? 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .x2-1m2-44x2-1 问题 3 观察上面等式右边的式子,对比等式左边的式子,你能发现什么规律?1.探索平方差公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .x2-1m2-44x2-1 问题 4 你能用字母总结这种规律吗?(a+b)(a-b) = a2-b21.探索平方差公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(x+1)(x-1) = ;
(2)(m+2)(m-2) = ;
(3)(2x+1)(2x-1) = .x2-1m2-44x2-1 问题 5 你能用文字语言总结这种规律吗? 两个数的和与这两个数的差的积,等于这两个数的平方差.1.探索平方差公式 平方差公式:两个数的和与这两个数的差的积,等于这两个数的平方差.(a+b)(a-b) = a2-b2 问题 6 你知道这个公式是如何推导的吗?2.理解平方差公式(a+b)(a-b)= a2-ab+ab-b2
= a2-b2 问题 7 你能根据图形说明平方差公式吗?3.深化平方差公式4.巩固平方差公式例 1 计算:
(1)(3x+2)(3x-2)
(2)(-x+2y)(-x-2y)解:(1) (3x+2)(3x-2) = (3x)2-22
= 9x2-44.巩固平方差公式例 1 计算:
(1)(3x+2)(3x-2)
(2)(-x+2y)(-x-2y)解:(2) (-x+2y)(-x-2y) = (-x)2-(2y)2
= x2-4y24.巩固平方差公式练习 1 下面各式计算得对不对?如果不对,该如何改正?
(1)(2a+3b)(2a-3b) = (2a)2 -(3b)2
(2)(2a-3b)(2a-3b) = (2a)2 -(3b)2
(3)(x+2)(x-2) = x2 -2
(4)(-3a-2)(3a-2) = 9a2 -4√× 4a2-12ab+9b2× x2-4× 4-9a24.巩固平方差公式 问题 8 通过例 1 和练习 1 的练习,你知道运用平方差公式时应该注意什么?(1)在运用平方差公式,一定要看是否具备公式的特征;(2)一定要找准哪一数或式相当于公式中的 a 和公式中的 b;(3)公式中的 a 、 b 可以具体是数、单项式、多项式;(4)不能忘记公式中的“平方”.4.巩固平方差公式例 2 计算:
(1)(-y+2)(-y-2)-(y-1)(y+5)
(2)102×98解:(1)原式= y2-4-y2-4y+5
= -4y+1 (2)原式= (100+2)(100-2)
= 10000-4
= 99964.巩固平方差公式练习 2 计算:
(1)(a+3b)(a-3b)
(2)(3+2a)(-3+2a)
(3)51×49
(4)(3x+4)(3x-4)-(2x+3)(2x-3)解:(1)原式= a2-9b2(2)原式= (2a+3)(2a-3)
= (2a)2 -32
= (22)a -32
= 4a -9(3)原式= (50+1)(50-1)
= 2500-1
= 2499(4)原式= 9x2 -16-4x2 +9
= 5x2 -75.拓广平方差公式练习 3 计算:
(1)(-a+b)(a+b);
(2)(-a-b)(-a+b);
(3)(a-b)(-a-b).5.拓广平方差公式 问题 9 通过练习 3,你可以总结出平方差公式的其他形式吗? (-a+b)(a+b) = b2-a2;
(-a-b)(-a+b) = a2-b2;
(a-b)(-a-b) = b2-a2.5.拓广平方差公式练习 4 计算:
(1)(x+3)(x-3)(x2+9)
(2)20132-2012×2014解:(1)原式= (x2-9)(x2+9)
= x4 -81(2)原式= 20132-(2013-1)(2013+1)
= 20132-20132+1
= 15.拓广平方差公式例 3 观察下列等式:
① 1×3+1=22;
② 3×5+1=42;
③ 5×7+1=62.(1)从上面三个等式可以发现有什么规律? 两个连续奇数的积与 1 的和,等于夹在这两个奇数中间的偶数的平方.(2)设 2k(k 是自然数)是一个偶数,按(1)中的规律可以得等式:(2k-1)(2k+1)+1 = 4k25.拓广平方差公式例 3 观察下列等式:
① 1×3+1=22;
② 3×5+1=42;
③ 5×7+1=62.(3)如何证明 (2k-1)(2k+1)+1 = 4k2 是正确的?证明:(2k-1)(2k+1)+1
= 4k2 -1+1
= 4k2
