14.2.2乘法公式--完全平方公式(第1课时)
文档属性
| 名称 | 14.2.2乘法公式--完全平方公式(第1课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-13 13:10:37 | ||
图片预览








文档简介
课件22张PPT。八年级 上册14.2.2 完全平方公式(第1课时)课件说明 我们在之前已经学习了多项式与多项式的乘法。那么,当有一些特殊的多项式与多项式相乘的式子,它们有哪些运算规律呢?让我们带着这个问题,开始进行 14.2 节的学习。14.2.2 完全平方公式(第1课时)
课件说明学习重点
完全平方公式。
学习目标
通过学习本课内容,首先学会利用完全平方公式的运算性质进行有规律的运算;其次将新知识与旧知识进行类比、区别,从而掌握完全平方公式的运算性质与理解数学中符号意识和数形结合思想。1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 2 观察上面等式左边的式子,你能发现什么规律? 等式左边的式子都是完全平方式;其中(1)中等式左边的式子是完全平方和式,(2)中等式左边的式子是完全平方差式.1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 3 观察上面等式右边的式子,对比等式左边的式子,你能发现什么规律?1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 4 你能用字母总结这种规律吗?(a+b)2 = a2+2ab+b2;
(a-b)2 = a2-2ab+b2.1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 5 你能用文字语言总结这种规律吗? 两个数的和(或差)的平方,等与它们的平方和,加上(或减去)它们的积的 2 倍.2.理解完全平方公式 两个数的和(或差)的平方,等与它们的平方和,加上(或减去)它们的积的 2 倍.(a+b)2 = a2+2ab+b2;
(a-b)2 = a2-2ab+b2. 问题 6 你知道这个公式是如何推导的吗?(a+b)2(a-b)2= (a+b)(a+b)
= a2+ab+ab+b2
= a2+2ab+b2= (a-b)(a-b)
= a2-ab-ab+b2
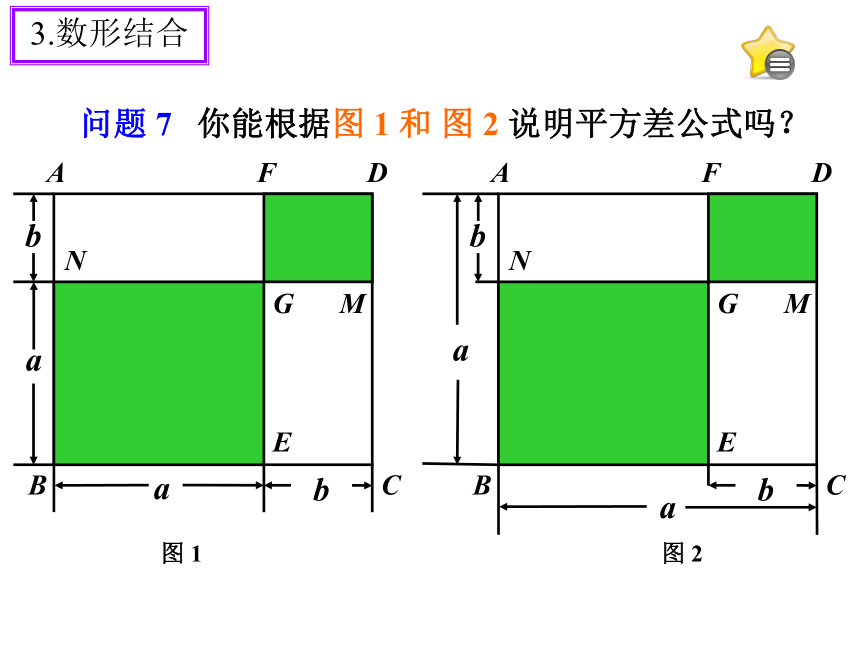
= a2-2ab+b2 问题 7 你能根据图 1 和 图 2 说明平方差公式吗?3.数形结合4.巩固完全平方公式例 1 运用完全平方公式计算:
(1)(4m+n)2
(2)( y- )212解:(1) (4m+n)2 = (4m)2+2 · (4m) · n+n2
= 16m2+8mn+n24.巩固完全平方公式例 1 运用完全平方公式计算:
(1)(4m+n)2
(2)( y- )2124.巩固完全平方公式练习 1 下面各式计算得对不对?如果不对,该如何改正?
(1)(a+b)2 = a2 +b2
(2)(a-b)2 = a2 -b2
(3)(x-y)2 = x2 +2xy+y2
(4)(x+y)2 = x2 +xy+y2× a2+2ab+b2× a2-2ab+b2× x2-2xy+y2× x2+2xy+y24.巩固完全平方公式 问题 8 通过例 1 和练习 1 的练习,你知道运用完全平方公式时应该注意什么?(1)积为二次三项式;(2)积中两项为积的平方和;(3)另一项是两数积的 2 倍,且与乘式中的符号相同;(4)公式中的 a 、 b 可以具体是数、单项式、多项式.巧计:首平方,尾平方,首尾两倍中间放.4.巩固完全平方公式例 2 运用完全平方公式计算:
(1)1022
(2)992解:(1)原式= (100+2)2
= 10000+400+4
= 10404(2)原式= (100-1)2
= 10000-200+1
= 98014.巩固完全平方公式练习 2 运用完全平方公式计算:
(1)(a+5)2
(2)(y-7)2
(3)(3+x)2
(4)(2-y)2= a2+10a+25= y2 -14a+49= 9+6x+x2= 4-4y+y25.拓广完全平方公式 问题 9 思考:
(1)(a+b)2 与 (-a-b)2 相等吗?
(2)(a-b)2 与 (b-a)2 相等吗?
(3)(a-b)2 与 a2-b2 相等吗?为什么?答:(1)(a+b)2 = (-a-b)2
证明:∵右边= (-a-b)2
= [-(a+b)]2
= (a+b)2
又∵左边= (a+b)2
∴左边=右边
∴(a+b)2 = (-a-b)2 问题 9 思考:
(1)(a+b)2 与 (-a-b)2 相等吗?
(2)(a-b)2 与 (b-a)2 相等吗?
(3)(a-b)2 与 a2-b2 相等吗?为什么?答:(2)(a-b)2 = (b-a)2
证明:∵右边= (b-a)2
= (-a+b)2
= [-(a-b)]2
= (a-b)2
又∵左边= (a-b)2
∴左边=右边
∴(a-b)2 = (b-a)25.拓广完全平方公式 问题 9 思考:
(1)(a+b)2 与 (-a-b)2 相等吗?
(2)(a-b)2 与 (b-a)2 相等吗?
(3)(a-b)2 与 a2-b2 相等吗?为什么?答:(3)(a-b)2 ≠ a2-b2
证明:∵左边= (a-b)2
= a2-2ab+b2
又∵右边= a2-b2
∴左边≠右边
∴(a-b)2 ≠ a2-b25.拓广完全平方公式5.拓广完全平方公式练习 3 运用完全平方公式计算:
(1)(3- )2
(2)(2x+3y)2
(3)(-2x+3y)2
(4)(- +3y)2t 3x2= 4x2+12xy+9y2解:(3)原式= (3y-2x)2
= 9y2-12xy+4x2 问题 10 通过问题 9 和练习 3 的练习,你知道运用完全平方公式时应该注意什么?5.拓广完全平方公式(1)有些整式相乘需要先左适当变形,然后再用公式;(2)在进行分数的平方运算时,要把分子、分母分别平方.5.拓广完全平方公式例 3 已知 a-b=3,ab=10,求下列各式的值.
(1)a2+b2;
(2)a+b.解:(1)原式= (a-b)2+2ab
= 32+2×10
= 9+20
= 295.拓广完全平方公式例 3 已知 a-b=3,ab=10,求下列各式的值.
(1)a2+b2;
(2)a+b.解:(2)∵(a+b)2 = (a-b)2+4ab
= 32+4×10
= 9+40
= 49
∴a+b = ±7
完全平方公式。
学习目标
通过学习本课内容,首先学会利用完全平方公式的运算性质进行有规律的运算;其次将新知识与旧知识进行类比、区别,从而掌握完全平方公式的运算性质与理解数学中符号意识和数形结合思想。1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 2 观察上面等式左边的式子,你能发现什么规律? 等式左边的式子都是完全平方式;其中(1)中等式左边的式子是完全平方和式,(2)中等式左边的式子是完全平方差式.1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 3 观察上面等式右边的式子,对比等式左边的式子,你能发现什么规律?1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 4 你能用字母总结这种规律吗?(a+b)2 = a2+2ab+b2;
(a-b)2 = a2-2ab+b2.1.探索完全平方公式 问题 1 在 14.1 节中,我们学习了整式的乘法. 请你根据整式的乘法的意义,判断下列式子属于哪种运算,并计算出结果:
(1)(p+1)2 = ;
(m+2)2 = ;
(2)(p-1)2 = ;
(m-2)2 = .p2+2p+1m2+4m+4p2-2p+1m2-4m+4 问题 5 你能用文字语言总结这种规律吗? 两个数的和(或差)的平方,等与它们的平方和,加上(或减去)它们的积的 2 倍.2.理解完全平方公式 两个数的和(或差)的平方,等与它们的平方和,加上(或减去)它们的积的 2 倍.(a+b)2 = a2+2ab+b2;
(a-b)2 = a2-2ab+b2. 问题 6 你知道这个公式是如何推导的吗?(a+b)2(a-b)2= (a+b)(a+b)
= a2+ab+ab+b2
= a2+2ab+b2= (a-b)(a-b)
= a2-ab-ab+b2
= a2-2ab+b2 问题 7 你能根据图 1 和 图 2 说明平方差公式吗?3.数形结合4.巩固完全平方公式例 1 运用完全平方公式计算:
(1)(4m+n)2
(2)( y- )212解:(1) (4m+n)2 = (4m)2+2 · (4m) · n+n2
= 16m2+8mn+n24.巩固完全平方公式例 1 运用完全平方公式计算:
(1)(4m+n)2
(2)( y- )2124.巩固完全平方公式练习 1 下面各式计算得对不对?如果不对,该如何改正?
(1)(a+b)2 = a2 +b2
(2)(a-b)2 = a2 -b2
(3)(x-y)2 = x2 +2xy+y2
(4)(x+y)2 = x2 +xy+y2× a2+2ab+b2× a2-2ab+b2× x2-2xy+y2× x2+2xy+y24.巩固完全平方公式 问题 8 通过例 1 和练习 1 的练习,你知道运用完全平方公式时应该注意什么?(1)积为二次三项式;(2)积中两项为积的平方和;(3)另一项是两数积的 2 倍,且与乘式中的符号相同;(4)公式中的 a 、 b 可以具体是数、单项式、多项式.巧计:首平方,尾平方,首尾两倍中间放.4.巩固完全平方公式例 2 运用完全平方公式计算:
(1)1022
(2)992解:(1)原式= (100+2)2
= 10000+400+4
= 10404(2)原式= (100-1)2
= 10000-200+1
= 98014.巩固完全平方公式练习 2 运用完全平方公式计算:
(1)(a+5)2
(2)(y-7)2
(3)(3+x)2
(4)(2-y)2= a2+10a+25= y2 -14a+49= 9+6x+x2= 4-4y+y25.拓广完全平方公式 问题 9 思考:
(1)(a+b)2 与 (-a-b)2 相等吗?
(2)(a-b)2 与 (b-a)2 相等吗?
(3)(a-b)2 与 a2-b2 相等吗?为什么?答:(1)(a+b)2 = (-a-b)2
证明:∵右边= (-a-b)2
= [-(a+b)]2
= (a+b)2
又∵左边= (a+b)2
∴左边=右边
∴(a+b)2 = (-a-b)2 问题 9 思考:
(1)(a+b)2 与 (-a-b)2 相等吗?
(2)(a-b)2 与 (b-a)2 相等吗?
(3)(a-b)2 与 a2-b2 相等吗?为什么?答:(2)(a-b)2 = (b-a)2
证明:∵右边= (b-a)2
= (-a+b)2
= [-(a-b)]2
= (a-b)2
又∵左边= (a-b)2
∴左边=右边
∴(a-b)2 = (b-a)25.拓广完全平方公式 问题 9 思考:
(1)(a+b)2 与 (-a-b)2 相等吗?
(2)(a-b)2 与 (b-a)2 相等吗?
(3)(a-b)2 与 a2-b2 相等吗?为什么?答:(3)(a-b)2 ≠ a2-b2
证明:∵左边= (a-b)2
= a2-2ab+b2
又∵右边= a2-b2
∴左边≠右边
∴(a-b)2 ≠ a2-b25.拓广完全平方公式5.拓广完全平方公式练习 3 运用完全平方公式计算:
(1)(3- )2
(2)(2x+3y)2
(3)(-2x+3y)2
(4)(- +3y)2t 3x2= 4x2+12xy+9y2解:(3)原式= (3y-2x)2
= 9y2-12xy+4x2 问题 10 通过问题 9 和练习 3 的练习,你知道运用完全平方公式时应该注意什么?5.拓广完全平方公式(1)有些整式相乘需要先左适当变形,然后再用公式;(2)在进行分数的平方运算时,要把分子、分母分别平方.5.拓广完全平方公式例 3 已知 a-b=3,ab=10,求下列各式的值.
(1)a2+b2;
(2)a+b.解:(1)原式= (a-b)2+2ab
= 32+2×10
= 9+20
= 295.拓广完全平方公式例 3 已知 a-b=3,ab=10,求下列各式的值.
(1)a2+b2;
(2)a+b.解:(2)∵(a+b)2 = (a-b)2+4ab
= 32+4×10
= 9+40
= 49
∴a+b = ±7
