3.1探索勾股定理(第2课时)
图片预览
文档简介
3.1探索勾股定理(第二课时)
学习目标
1、初步掌握证明勾股定理的思路与方法
2、会利用勾股定理进行简单的证明与计算
学习重难点
证明勾股定理,利用勾股定理
学习过程
一、知识衔接
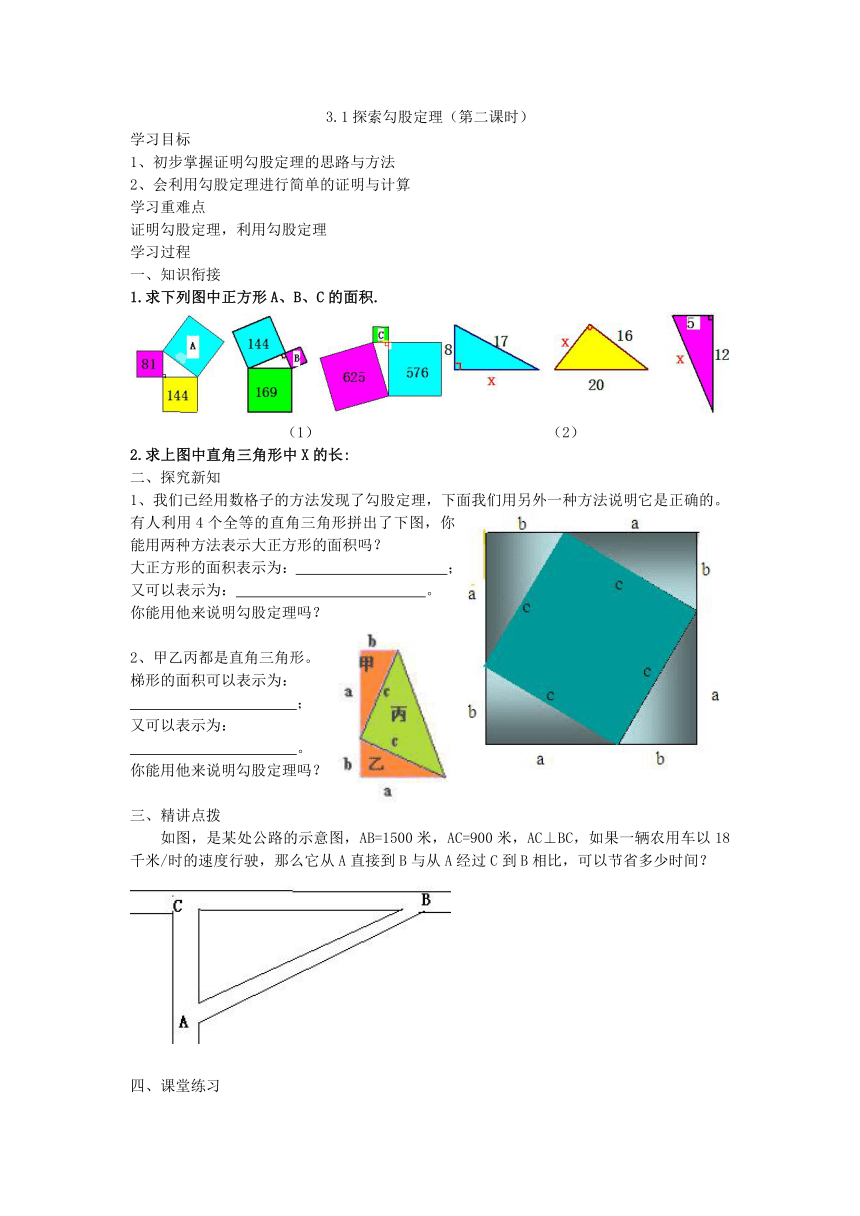
1.求下列图中正方形A、B、C的面积.
(1) (2)
2.求上图中直角三角形中X的长:
二、探究新知
1、我们已经用数格子的方法发现了勾股定理,下面我们用另外一种方法说明它是正确的。
有人利用4个全等的直角三角形拼出了下图,你能用两种方法表示大正方形的面积吗?
大正方形的面积表示为: ;
又可以表示为: 。
你能用他来说明勾股定理吗?
2、甲乙丙都是直角三角形。
梯形的面积可以表示为:
;
又可以表示为:
。
你能用他来说明勾股定理吗?
三、精讲点拨
如图,是某处公路的示意图,AB=1500米,AC=900米,AC⊥BC,如果一辆农用车以18千米/时的速度行驶,那么它从A直接到B与从A经过C到B相比,可以节省多少时间?
四、课堂练习
1、如图,从电线杆OA的顶端A点,扯一根钢丝绳固定在地面上的B点,这根钢丝绳的长度是多少?
2、如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?3、已知一个Rt△ABC的两边长分别为3和4,则第三边长的平方是 ;
4、如图,校园内有两棵树,相距12米,一棵树高为13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
5、图中的阴影部分是一个正方形,则这个正方形的面积是 。
五、本节小结
本节课我学习了什么?
六、当堂测试
1.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
2.图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是 .
3.折竹抵地(源自《九章算术》):今有竹高一丈,末折抵地,去本三尺.问折者高几何 意即: 一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原长竹子处3尺远.问原处还有多高的竹子
学习目标
1、初步掌握证明勾股定理的思路与方法
2、会利用勾股定理进行简单的证明与计算
学习重难点
证明勾股定理,利用勾股定理
学习过程
一、知识衔接
1.求下列图中正方形A、B、C的面积.
(1) (2)
2.求上图中直角三角形中X的长:
二、探究新知
1、我们已经用数格子的方法发现了勾股定理,下面我们用另外一种方法说明它是正确的。
有人利用4个全等的直角三角形拼出了下图,你能用两种方法表示大正方形的面积吗?
大正方形的面积表示为: ;
又可以表示为: 。
你能用他来说明勾股定理吗?
2、甲乙丙都是直角三角形。
梯形的面积可以表示为:
;
又可以表示为:
。
你能用他来说明勾股定理吗?
三、精讲点拨
如图,是某处公路的示意图,AB=1500米,AC=900米,AC⊥BC,如果一辆农用车以18千米/时的速度行驶,那么它从A直接到B与从A经过C到B相比,可以节省多少时间?
四、课堂练习
1、如图,从电线杆OA的顶端A点,扯一根钢丝绳固定在地面上的B点,这根钢丝绳的长度是多少?
2、如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?3、已知一个Rt△ABC的两边长分别为3和4,则第三边长的平方是 ;
4、如图,校园内有两棵树,相距12米,一棵树高为13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞 米.
5、图中的阴影部分是一个正方形,则这个正方形的面积是 。
五、本节小结
本节课我学习了什么?
六、当堂测试
1.如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.
2.图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若,,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是 .
3.折竹抵地(源自《九章算术》):今有竹高一丈,末折抵地,去本三尺.问折者高几何 意即: 一根竹子,原高一丈,虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原长竹子处3尺远.问原处还有多高的竹子
