苏科版七年级数学平面图形《线段与角》拓展练习(无答案)
文档属性
| 名称 | 苏科版七年级数学平面图形《线段与角》拓展练习(无答案) | 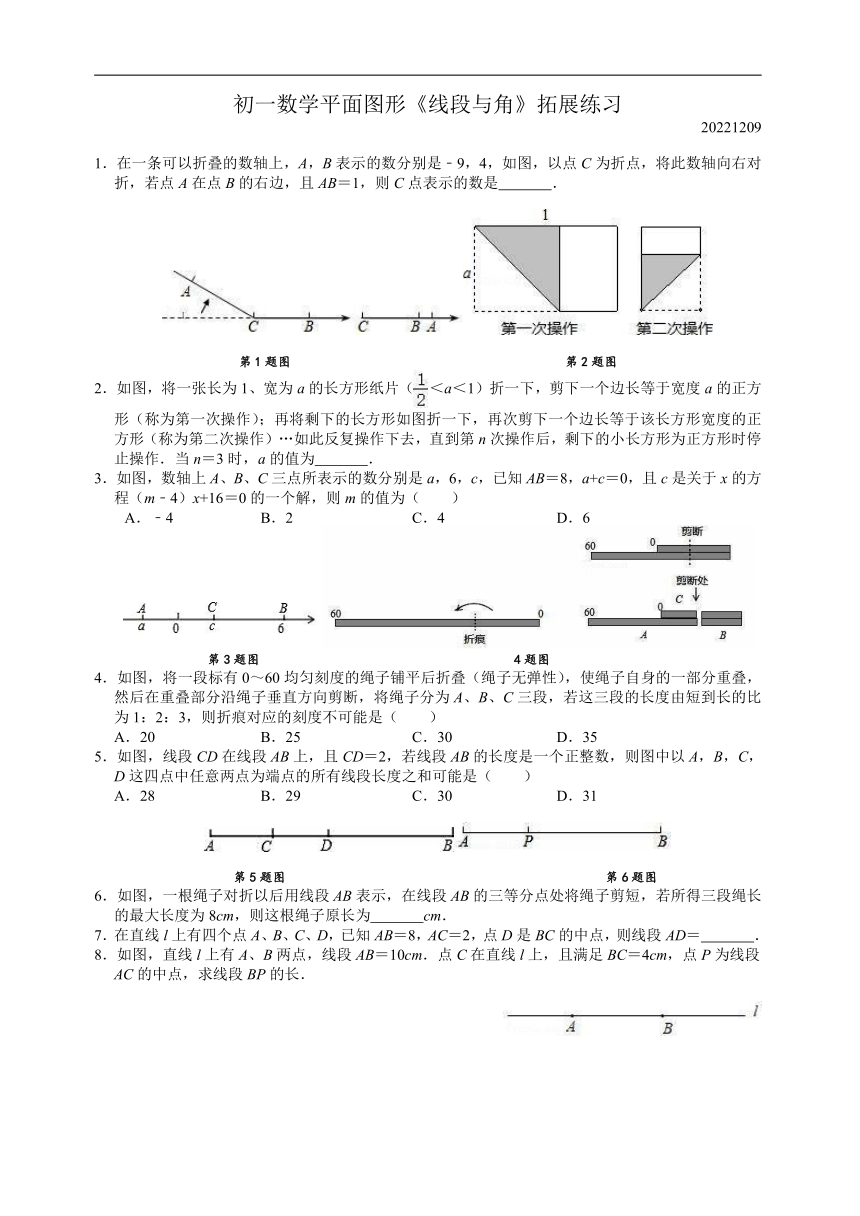 | |
| 格式 | docx | ||
| 文件大小 | 249.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-16 10:24:07 | ||
图片预览


文档简介
初一数学平面图形《线段与角》拓展练习
20221209
1.在一条可以折叠的数轴上,A,B表示的数分别是﹣9,4,如图,以点C为折点,将此数轴向右对折,若点A在点B的右边,且AB=1,则C点表示的数是 .
第1题图 第2题图
2.如图,将一张长为1、宽为a的长方形纸片(<a<1)折一下,剪下一个边长等于宽度a的正方形(称为第一次操作);再将剩下的长方形如图折一下,再次剪下一个边长等于该长方形宽度的正方形(称为第二次操作)…如此反复操作下去,直到第n次操作后,剩下的小长方形为正方形时停止操作.当n=3时,a的值为 .
3.如图,数轴上A、B、C三点所表示的数分别是a,6,c,已知AB=8,a+c=0,且c是关于x的方程(m﹣4)x+16=0的一个解,则m的值为( )
A.﹣4 B.2 C.4 D.6
第3题图 4题图
4.如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
A.20 B.25 C.30 D.35
5.如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
A.28 B.29 C.30 D.31
第5题图 第6题图
6.如图,一根绳子对折以后用线段AB表示,在线段AB的三等分点处将绳子剪短,若所得三段绳长的最大长度为8cm,则这根绳子原长为 cm.
7.在直线l上有四个点A、B、C、D,已知AB=8,AC=2,点D是BC的中点,则线段AD= .
8.如图,直线l上有A、B两点,线段AB=10cm.点C在直线l上,且满足BC=4cm,点P为线段AC的中点,求线段BP的长.
9.已知线段AB=12cm,C为线段AB上一点,BC=5cm,点D为AC的中点.求DB的长度.
10.已知,点C是线段AB的中点,AC=6.点D在线段AB上,且BD=AD,求线段CD的长.
11.如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=BC,求线段PQ的长.
12.如图,点C是AB上一点,点D是AC的中点,若AB=12,BD=7,求CB的长.
13.如图,是一副特制的三角板,用它们可以画出一些特殊角.在下列选项中,不能画出的角度是( )
A.18° B.55° C.63° D.117°
第13题图 14题图 第15题图 第16题图
14.如图,一副三角尺有公共的顶点A,则∠DAB﹣∠EAC= .
15.如图,直线AB、CD相交于点O,OE平分∠BOD;OF平分∠COE,若∠AOC=82°,则∠BOF
= °.
16.如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,
∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与
∠BOD互余,其中正确的有 (只填写正确结论的序号).
17.如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.
(1)若∠AOC=50°,则∠DOE= °;
(2)当∠AOC的大小发生改变时,∠DOE的大小
是否发生改变?为什么?
(3)图中与∠COD互补角的个数随∠AOC的度数
变化而变化,直接写出与∠COD互补的角的
个数及对应的∠AOC的度数.
18.如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE∶∠DOE=2∶3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
19.如下图,已知∠AOB=150°,∠AOC=40°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=10°,求∠COF的度数;
(2)若∠COF=10°,求∠EOB= ;
(3)若∠EOB=m°,求∠COF= ;(用含m的式子表示)
(4)若∠COF=n°,求∠EOB= .(用含n的式子表示)
图1 图2
20.如图1,点A,O,B依次在直线MN上.将射线OA绕点O沿顺时针方向以每秒18°的速度旋转,
同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2).设旋转时间为t(0≤t≤30,
单位秒).
(1)当t=10时,∠AOB= °;
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°
而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=45°时,求t的值.
21.一个问题解决往往经历发现猜想→探索归纳→问题解决的过程,下面结合一道几何题来体验一下.
【发现猜想】如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;
【探索归纳】如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线.猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
【问题解决】如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动.运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
22.如图,点O在直线AB上,OC、OD是两条射线,OC⊥OD,射线OE平分∠BOC.
(1)若∠DOE=150°,求∠AOC的度数.
(2)若∠DOE=α,则∠AOC= .(请用含α的代数式表示)
23.已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC=60°.
(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=∠BOD,求∠DOE
的度数;
(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF绕着O
点从OB开始以5度/秒的速度逆时针旋转至OA结束,运动时间为t秒,当∠EOC=∠FOC
时,求t的值:
(3)若射线OM绕着O点从OA开始以15度/秒的速度逆时针旋转至OB结束,在旋转过程中,
ON平分∠AOM,试问2∠BON一∠BOM在某时间段内是否为定值,若不是,请说明理由;
若是请补全图形,求出这个定值并写出t所在的时间段.(本题中的角均为大于0°且小于
180°的角)
24.如图,AC⊥CB,垂足为C,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC
方向匀速移动,速度为2cm/s.设动点P运动的时间为ts,记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
(1)S3= cm2(用含t的代数式表示);
(2)当S1=S时,求运动时间t;
(3)是否存在某一时刻,使得S1=S2=S3,若存在,求出t值,若不存在,说明理由.
20221209
1.在一条可以折叠的数轴上,A,B表示的数分别是﹣9,4,如图,以点C为折点,将此数轴向右对折,若点A在点B的右边,且AB=1,则C点表示的数是 .
第1题图 第2题图
2.如图,将一张长为1、宽为a的长方形纸片(<a<1)折一下,剪下一个边长等于宽度a的正方形(称为第一次操作);再将剩下的长方形如图折一下,再次剪下一个边长等于该长方形宽度的正方形(称为第二次操作)…如此反复操作下去,直到第n次操作后,剩下的小长方形为正方形时停止操作.当n=3时,a的值为 .
3.如图,数轴上A、B、C三点所表示的数分别是a,6,c,已知AB=8,a+c=0,且c是关于x的方程(m﹣4)x+16=0的一个解,则m的值为( )
A.﹣4 B.2 C.4 D.6
第3题图 4题图
4.如图,将一段标有0~60均匀刻度的绳子铺平后折叠(绳子无弹性),使绳子自身的一部分重叠,然后在重叠部分沿绳子垂直方向剪断,将绳子分为A、B、C三段,若这三段的长度由短到长的比为1:2:3,则折痕对应的刻度不可能是( )
A.20 B.25 C.30 D.35
5.如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
A.28 B.29 C.30 D.31
第5题图 第6题图
6.如图,一根绳子对折以后用线段AB表示,在线段AB的三等分点处将绳子剪短,若所得三段绳长的最大长度为8cm,则这根绳子原长为 cm.
7.在直线l上有四个点A、B、C、D,已知AB=8,AC=2,点D是BC的中点,则线段AD= .
8.如图,直线l上有A、B两点,线段AB=10cm.点C在直线l上,且满足BC=4cm,点P为线段AC的中点,求线段BP的长.
9.已知线段AB=12cm,C为线段AB上一点,BC=5cm,点D为AC的中点.求DB的长度.
10.已知,点C是线段AB的中点,AC=6.点D在线段AB上,且BD=AD,求线段CD的长.
11.如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=BC,求线段PQ的长.
12.如图,点C是AB上一点,点D是AC的中点,若AB=12,BD=7,求CB的长.
13.如图,是一副特制的三角板,用它们可以画出一些特殊角.在下列选项中,不能画出的角度是( )
A.18° B.55° C.63° D.117°
第13题图 14题图 第15题图 第16题图
14.如图,一副三角尺有公共的顶点A,则∠DAB﹣∠EAC= .
15.如图,直线AB、CD相交于点O,OE平分∠BOD;OF平分∠COE,若∠AOC=82°,则∠BOF
= °.
16.如图,已知OA⊥OB,点O为垂足,OC是∠AOB内任意一条射线,OB,OD分别平分∠COD,
∠BOE,下列结论:①∠COD=∠BOE;②∠COE=3∠BOD;③∠BOE=∠AOC;④∠AOC与
∠BOD互余,其中正确的有 (只填写正确结论的序号).
17.如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.
(1)若∠AOC=50°,则∠DOE= °;
(2)当∠AOC的大小发生改变时,∠DOE的大小
是否发生改变?为什么?
(3)图中与∠COD互补角的个数随∠AOC的度数
变化而变化,直接写出与∠COD互补的角的
个数及对应的∠AOC的度数.
18.如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE∶∠DOE=2∶3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
19.如下图,已知∠AOB=150°,∠AOC=40°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=10°,求∠COF的度数;
(2)若∠COF=10°,求∠EOB= ;
(3)若∠EOB=m°,求∠COF= ;(用含m的式子表示)
(4)若∠COF=n°,求∠EOB= .(用含n的式子表示)
图1 图2
20.如图1,点A,O,B依次在直线MN上.将射线OA绕点O沿顺时针方向以每秒18°的速度旋转,
同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2).设旋转时间为t(0≤t≤30,
单位秒).
(1)当t=10时,∠AOB= °;
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°
而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=45°时,求t的值.
21.一个问题解决往往经历发现猜想→探索归纳→问题解决的过程,下面结合一道几何题来体验一下.
【发现猜想】如图①,已知∠AOB=70°,∠AOD=100°,OC为∠BOD的角平分线,则∠AOC的度数为 ;
【探索归纳】如图①,∠AOB=m,∠AOD=n,OC为∠BOD的角平分线.猜想∠AOC的度数(用含m、n的代数式表示),并说明理由.
【问题解决】如图②,若∠AOB=20°,∠AOC=90°,∠AOD=120°.若射线OB绕点O以每秒20°逆时针旋转,射线OC绕点O以每秒10°顺时针旋转,射线OD绕点O每秒30°顺时针旋转,三条射线同时旋转,当一条射线与直线OA重合时,三条射线同时停止运动.运动几秒时,其中一条射线是另外两条射线夹角的角平分线?
22.如图,点O在直线AB上,OC、OD是两条射线,OC⊥OD,射线OE平分∠BOC.
(1)若∠DOE=150°,求∠AOC的度数.
(2)若∠DOE=α,则∠AOC= .(请用含α的代数式表示)
23.已知∠AOB=150°,OC为∠AOB内部的一条射线,∠BOC=60°.
(1)如图1,若OE平分∠AOB,OD为∠BOC内部的一条射线,∠COD=∠BOD,求∠DOE
的度数;
(2)如图2,若射线OE绕着O点从OA开始以15度/秒的速度顺时针旋转至OB结束、OF绕着O
点从OB开始以5度/秒的速度逆时针旋转至OA结束,运动时间为t秒,当∠EOC=∠FOC
时,求t的值:
(3)若射线OM绕着O点从OA开始以15度/秒的速度逆时针旋转至OB结束,在旋转过程中,
ON平分∠AOM,试问2∠BON一∠BOM在某时间段内是否为定值,若不是,请说明理由;
若是请补全图形,求出这个定值并写出t所在的时间段.(本题中的角均为大于0°且小于
180°的角)
24.如图,AC⊥CB,垂足为C,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC
方向匀速移动,速度为2cm/s.设动点P运动的时间为ts,记三角形ABC面积为S,三角形PCQ的面积为S1,三角形PAQ的面积为S2,三角形ABP的面积为S3.
(1)S3= cm2(用含t的代数式表示);
(2)当S1=S时,求运动时间t;
(3)是否存在某一时刻,使得S1=S2=S3,若存在,求出t值,若不存在,说明理由.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
