人教版数学八年级上册 专题五 作图专题课件(共28张PPT)
文档属性
| 名称 | 人教版数学八年级上册 专题五 作图专题课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-16 10:59:33 | ||
图片预览



文档简介
(共28张PPT)
第三部分 专题探究
专题五 作图专题
目录
01
考点突破
02
变式诊断
03
基础训练
04
拓展提升
考点一:作角平分线及综合运用
考点突破
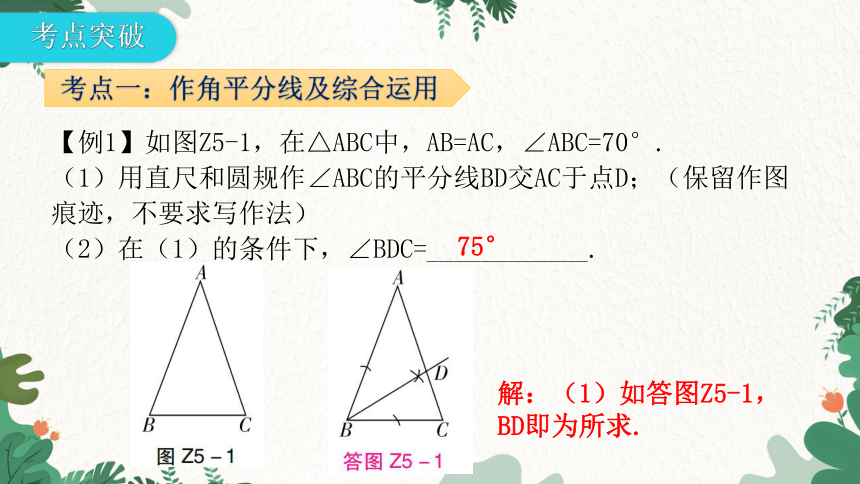
【例1】如图Z5-1,在△ABC中,AB=AC,∠ABC=70°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D;(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,∠BDC=____________.
75°
解:(1)如答图Z5-1,BD即为所求.
变式诊断
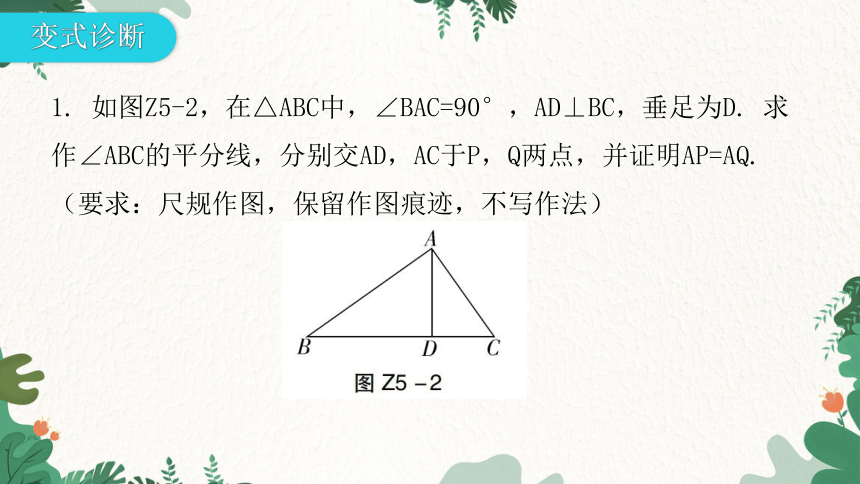
1. 如图Z5-2,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D. 求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ. (要求:尺规作图,保留作图痕迹,不写作法)
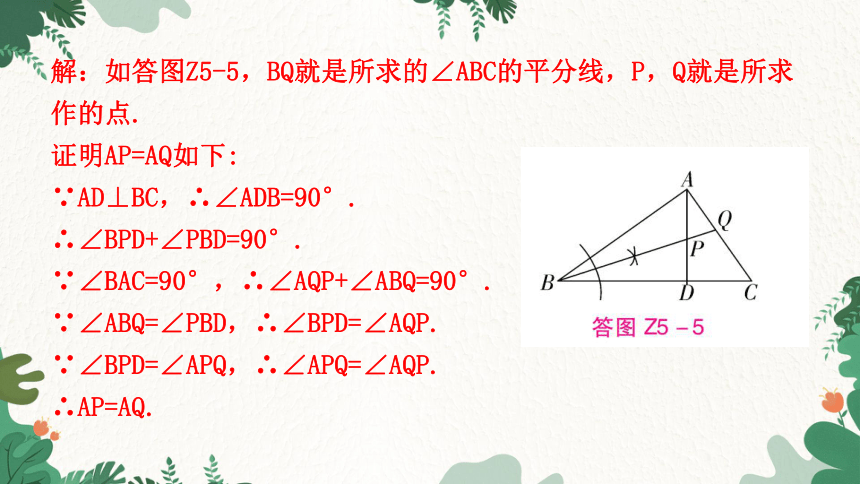
解:如答图Z5-5,BQ就是所求的∠ABC的平分线,P,Q就是所求作的点.
证明AP=AQ如下:
∵AD⊥BC,∴∠ADB=90°.
∴∠BPD+∠PBD=90°.
∵∠BAC=90°,∴∠AQP+∠ABQ=90°.
∵∠ABQ=∠PBD,∴∠BPD=∠AQP.
∵∠BPD=∠APQ,∴∠APQ=∠AQP.
∴AP=AQ.
考点突破
考点二:作垂直平分线及综合运用
【例2】如图Z5-3,在△ABC中,AB=AC,点D在边AB上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D;(不写作法,但保留作图痕迹)
(2)若BC=5,周长为21,求△BCD的周长.
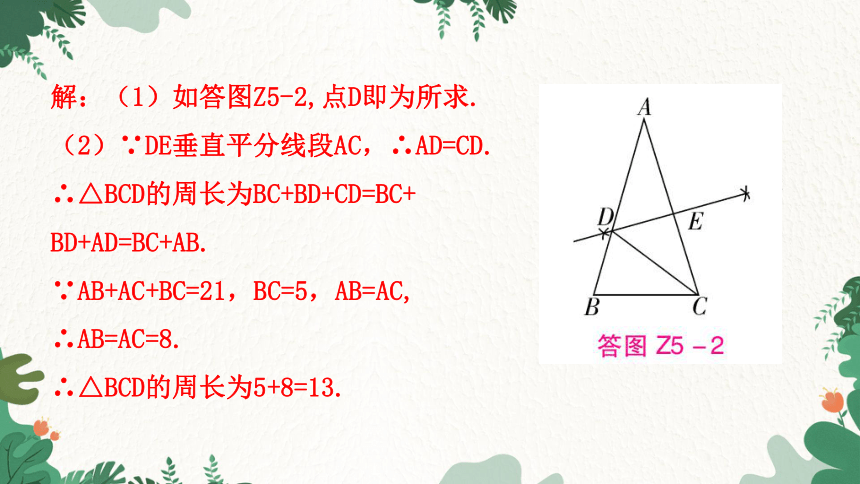
解:(1)如答图Z5-2,点D即为所求.
(2)∵DE垂直平分线段AC,∴AD=CD.
∴△BCD的周长为BC+BD+CD=BC+
BD+AD=BC+AB.
∵AB+AC+BC=21,BC=5,AB=AC,
∴AB=AC=8.
∴△BCD的周长为5+8=13.
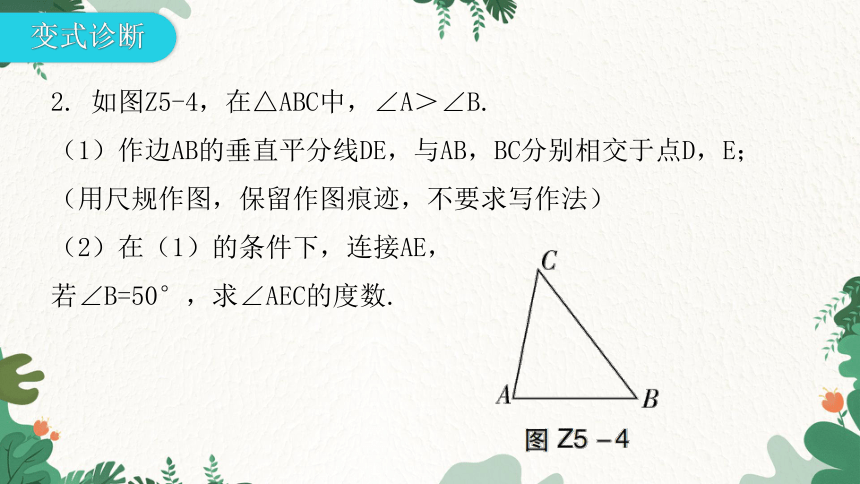
2. 如图Z5-4,在△ABC中,∠A>∠B.
(1)作边AB的垂直平分线DE,与AB,BC分别相交于点D,E;(用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)的条件下,连接AE,
若∠B=50°,求∠AEC的度数.
变式诊断
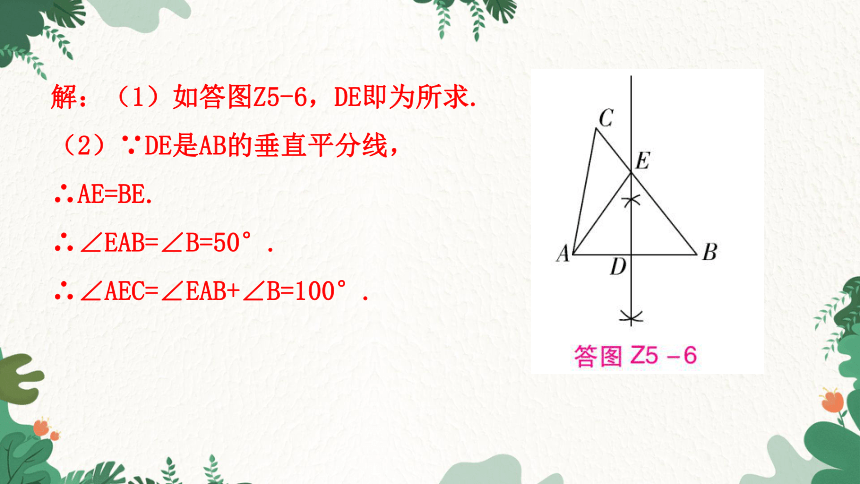
解:(1)如答图Z5-6,DE即为所求.
(2)∵DE是AB的垂直平分线,
∴AE=BE.
∴∠EAB=∠B=50°.
∴∠AEC=∠EAB+∠B=100°.
考点突破
考点三:过一点作直线的垂线
【例3】如图Z5-5,已知点P在直线l上,请过点P作直线l的垂
线PA.
略.
变式诊断
3.如图Z5-6,已知点P在直线l外,过点P作直线l的垂线PA.
略.
考点突破
考点四:作一个角等于已知角
【例4】如图Z5-7,作一个角等于∠AOB.
解: 如答图Z5-3,∠A′O′B′即为所求.
4. 如图Z5-8,在△ABC中,∠ACB>∠ABC. 用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC.(不要求写作法,保留作图痕迹)
变式诊断
解:如答图Z5-7,射线CM即为所求.
考点突破
考点五:最短路径问题作图
【例5】如图Z5-9,铁路l的同侧有A,B两个工厂,要在路边建一个货物站C,使A,B两厂到货物站C的距离之和最小,请作出货物站C的位置.
解:如答图Z5-4,点C即为所求.
5. 如图Z5-10,∠AOB的内部有一点P,在射线OA,OB上各取一
点P1,P2,使得△PP1P2的周长最小.(不要求写作法,保留作图痕迹)
变式诊断
解:如答图Z5-8,△PP1P2即为所求.
考点突破
考点六:网格作图
【例6】如图Z5-11,已知△ABC,
画出△ABC关于y轴对称的图形
△A1B1C1,并写出△A1B1C1各顶点
的坐标.
解:画图略.A1(-3,4),
B1(-1,2),C1(-5,1).
6. 如图Z5-12,已知△ABC.画出
△ABC关于x轴对称的图形△A1B1C1,
并写出△A1B1C1各顶点的坐标.
变式诊断
解:画图略.
A1(0,2),
B1(2,4),
C1(4,1).
基础训练
7. △ABC在方格纸中的位置如图Z5-13:
(1)请在方格纸上建立平面直角坐标系,
使得A,B两点的坐标分别为A(2,-1),
B(1,-4),并求出点C的坐标;
(2)画出△ABC关于x轴对称的△A1B1C1,
并写出点A1,B1,C1的坐标.
解:(1)建立的平面直角坐标系如答图Z5-9,C(3,-3).
(2)如答图Z5-9,
△A1B1C1即为所求,
A1(2,1),
B1(1,4),
C1(3,3).
8. 如图Z5-14,在平面直角坐标系中,先描出点A(1,3),B(4,1).
(1)用尺规在x轴上找一点C,使AC+BC的值最小; (保留作图痕迹)
(2)用尺规在x轴上找一点P,使PA=PB.(保留作图痕迹)
解:(1)如答图Z5-10,点C即为所求.
(2)如答图Z5-10,点P即为所求.
9. 如图Z5-15,在直线MN上求作一点P,使点P到射线OA和OB的距离相等. (不要求写作法,但要保留作图痕迹)
解:如答图Z5-11,点P即为所求.
10. 如图Z5-16,已知四边形ABCD.求作点P,使∠PCB=∠B,且点P到点C和点D的距离相等. (用圆规、直尺作图,不写作法,但要保留作图痕迹)
拓展提升
解:如答图Z5-12,点P即为所求.
11.如图Z5-17,已知△ABC,∠BAC=90°.
(1)尺规作图:作边BC的高AD;(保留作图痕迹,不写作法)
(2)求证:∠C=∠BAD.
(1)解:如答图Z5-13,AD即为所求.
(2)证明:∵∠BAC=90°,
∴∠BAD+∠CAD=90°.
∵AD是△ABC的高,
∴AD⊥BC,
∴∠CDA=90°.
在Rt△CAD中,∠C+∠CAD=90°,
∴∠C=∠BAD.
12. 如图Z5-18,已知甲村和乙村靠近公路a,b,为了发展经济,甲、乙两村准备合建一个工厂,经协商,工厂必须满足以下要求:
(1)到两村的距离相等;
(2)到两条公路的距离相等.
你能帮忙确定工厂的位置吗?
谢 谢
第三部分 专题探究
专题五 作图专题
目录
01
考点突破
02
变式诊断
03
基础训练
04
拓展提升
考点一:作角平分线及综合运用
考点突破
【例1】如图Z5-1,在△ABC中,AB=AC,∠ABC=70°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D;(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,∠BDC=____________.
75°
解:(1)如答图Z5-1,BD即为所求.
变式诊断
1. 如图Z5-2,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D. 求作∠ABC的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ. (要求:尺规作图,保留作图痕迹,不写作法)
解:如答图Z5-5,BQ就是所求的∠ABC的平分线,P,Q就是所求作的点.
证明AP=AQ如下:
∵AD⊥BC,∴∠ADB=90°.
∴∠BPD+∠PBD=90°.
∵∠BAC=90°,∴∠AQP+∠ABQ=90°.
∵∠ABQ=∠PBD,∴∠BPD=∠AQP.
∵∠BPD=∠APQ,∴∠APQ=∠AQP.
∴AP=AQ.
考点突破
考点二:作垂直平分线及综合运用
【例2】如图Z5-3,在△ABC中,AB=AC,点D在边AB上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D;(不写作法,但保留作图痕迹)
(2)若BC=5,周长为21,求△BCD的周长.
解:(1)如答图Z5-2,点D即为所求.
(2)∵DE垂直平分线段AC,∴AD=CD.
∴△BCD的周长为BC+BD+CD=BC+
BD+AD=BC+AB.
∵AB+AC+BC=21,BC=5,AB=AC,
∴AB=AC=8.
∴△BCD的周长为5+8=13.
2. 如图Z5-4,在△ABC中,∠A>∠B.
(1)作边AB的垂直平分线DE,与AB,BC分别相交于点D,E;(用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)的条件下,连接AE,
若∠B=50°,求∠AEC的度数.
变式诊断
解:(1)如答图Z5-6,DE即为所求.
(2)∵DE是AB的垂直平分线,
∴AE=BE.
∴∠EAB=∠B=50°.
∴∠AEC=∠EAB+∠B=100°.
考点突破
考点三:过一点作直线的垂线
【例3】如图Z5-5,已知点P在直线l上,请过点P作直线l的垂
线PA.
略.
变式诊断
3.如图Z5-6,已知点P在直线l外,过点P作直线l的垂线PA.
略.
考点突破
考点四:作一个角等于已知角
【例4】如图Z5-7,作一个角等于∠AOB.
解: 如答图Z5-3,∠A′O′B′即为所求.
4. 如图Z5-8,在△ABC中,∠ACB>∠ABC. 用直尺和圆规在∠ACB的内部作射线CM,使∠ACM=∠ABC.(不要求写作法,保留作图痕迹)
变式诊断
解:如答图Z5-7,射线CM即为所求.
考点突破
考点五:最短路径问题作图
【例5】如图Z5-9,铁路l的同侧有A,B两个工厂,要在路边建一个货物站C,使A,B两厂到货物站C的距离之和最小,请作出货物站C的位置.
解:如答图Z5-4,点C即为所求.
5. 如图Z5-10,∠AOB的内部有一点P,在射线OA,OB上各取一
点P1,P2,使得△PP1P2的周长最小.(不要求写作法,保留作图痕迹)
变式诊断
解:如答图Z5-8,△PP1P2即为所求.
考点突破
考点六:网格作图
【例6】如图Z5-11,已知△ABC,
画出△ABC关于y轴对称的图形
△A1B1C1,并写出△A1B1C1各顶点
的坐标.
解:画图略.A1(-3,4),
B1(-1,2),C1(-5,1).
6. 如图Z5-12,已知△ABC.画出
△ABC关于x轴对称的图形△A1B1C1,
并写出△A1B1C1各顶点的坐标.
变式诊断
解:画图略.
A1(0,2),
B1(2,4),
C1(4,1).
基础训练
7. △ABC在方格纸中的位置如图Z5-13:
(1)请在方格纸上建立平面直角坐标系,
使得A,B两点的坐标分别为A(2,-1),
B(1,-4),并求出点C的坐标;
(2)画出△ABC关于x轴对称的△A1B1C1,
并写出点A1,B1,C1的坐标.
解:(1)建立的平面直角坐标系如答图Z5-9,C(3,-3).
(2)如答图Z5-9,
△A1B1C1即为所求,
A1(2,1),
B1(1,4),
C1(3,3).
8. 如图Z5-14,在平面直角坐标系中,先描出点A(1,3),B(4,1).
(1)用尺规在x轴上找一点C,使AC+BC的值最小; (保留作图痕迹)
(2)用尺规在x轴上找一点P,使PA=PB.(保留作图痕迹)
解:(1)如答图Z5-10,点C即为所求.
(2)如答图Z5-10,点P即为所求.
9. 如图Z5-15,在直线MN上求作一点P,使点P到射线OA和OB的距离相等. (不要求写作法,但要保留作图痕迹)
解:如答图Z5-11,点P即为所求.
10. 如图Z5-16,已知四边形ABCD.求作点P,使∠PCB=∠B,且点P到点C和点D的距离相等. (用圆规、直尺作图,不写作法,但要保留作图痕迹)
拓展提升
解:如答图Z5-12,点P即为所求.
11.如图Z5-17,已知△ABC,∠BAC=90°.
(1)尺规作图:作边BC的高AD;(保留作图痕迹,不写作法)
(2)求证:∠C=∠BAD.
(1)解:如答图Z5-13,AD即为所求.
(2)证明:∵∠BAC=90°,
∴∠BAD+∠CAD=90°.
∵AD是△ABC的高,
∴AD⊥BC,
∴∠CDA=90°.
在Rt△CAD中,∠C+∠CAD=90°,
∴∠C=∠BAD.
12. 如图Z5-18,已知甲村和乙村靠近公路a,b,为了发展经济,甲、乙两村准备合建一个工厂,经协商,工厂必须满足以下要求:
(1)到两村的距离相等;
(2)到两条公路的距离相等.
你能帮忙确定工厂的位置吗?
谢 谢
