4.1 无理数(第2课时)学案
图片预览
文档简介
4.1无理数(第2课时)
学习目标:
1、 借助计算器探索无理数是无限不循环小数。
2、 会判断一个数是无理数还是有理数。
重点:理解无理数的认识。
难点:会判断一个数是无理数还是有理数,有理数与无理数的区别。
学习过程
一、知识衔接
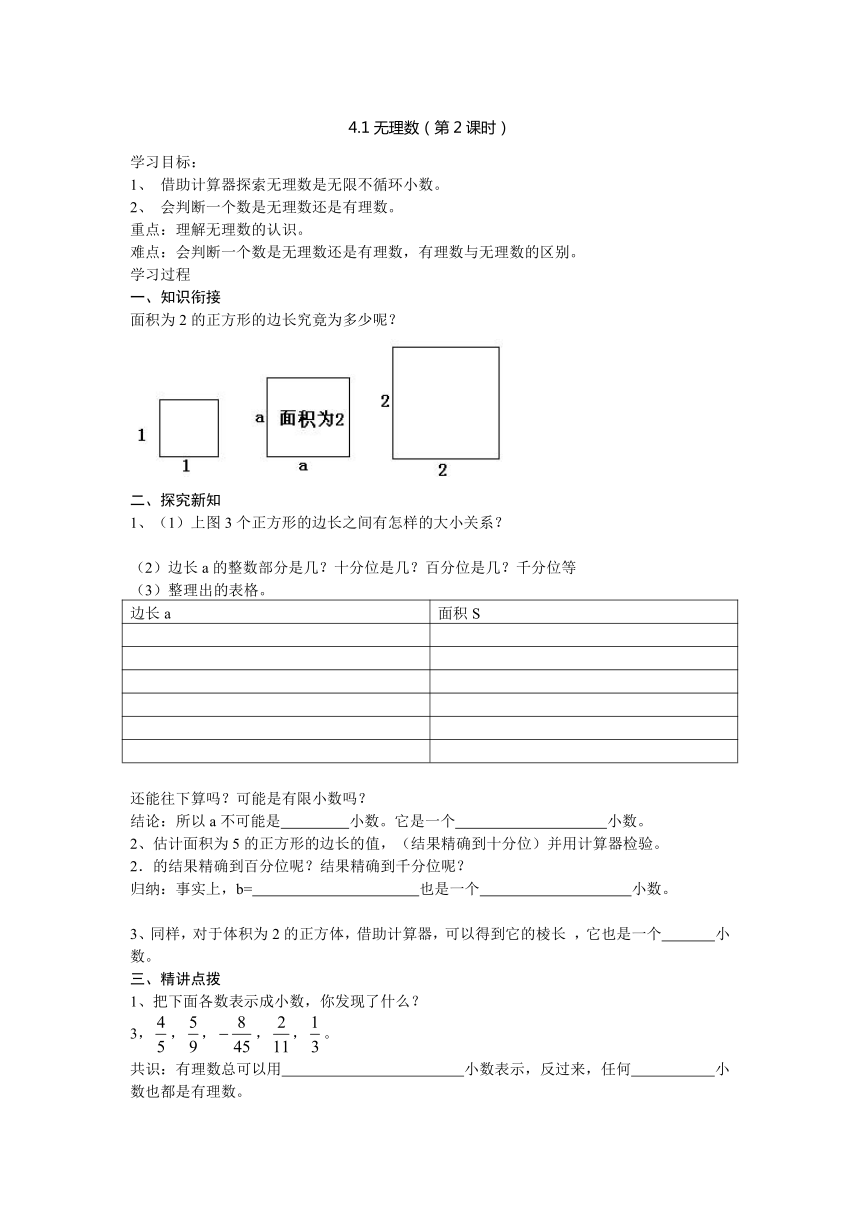
面积为2的正方形的边长究竟为多少呢?
二、探究新知
1、(1)上图3个正方形的边长之间有怎样的大小关系?
(2)边长a的整数部分是几?十分位是几?百分位是几?千分位等
(3)整理出的表格。
边长a 面积S
还能往下算吗?可能是有限小数吗?
结论:所以a不可能是 小数。它是一个 小数。
2、估计面积为5的正方形的边长的值,(结果精确到十分位)并用计算器检验。
2.的结果精确到百分位呢?结果精确到千分位呢?
归纳:事实上,b= 也是一个 小数。
3、同样,对于体积为2的正方体,借助计算器,可以得到它的棱长 ,它也是一个 小数。
三、精讲点拨
1、把下面各数表示成小数,你发现了什么?
3,,,,,。
共识:有理数总可以用 小数表示,反过来,任何 小数也都是有理数。
总结:无限不循环小数叫做无理数。
除了象上面的,,是无理数外,像我们熟悉的圆周率也是一个无限不循环小数,所以它也是无理数。
再如:(相邻两个5之间8的个数逐次增1)也是无理数。
四、随堂练习
1、下列各数中,哪些是有理数?哪些是无理数?
,,………,…(相邻两个1之间0的个数逐渐加1)。
2、判断下列说法是否正确:
(1)有限小数是有理数; ( )(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )(4)有理数是有限数. ( )
3、在0.351,-,4.969696…,6.751755175551…,0,-5.2333,5.411010010001…中,无理数的个数有______.
4、面积为6的长方形,长是宽的2倍,则宽为( )21世纪教育网
A.小数 B.分数 C.无理数 D.不能确定21世纪教育网
5、面积为3的正方形的边长______有理数;面积为4的正方形的边长______有理数.(填“是”或“不是”)
6、一个高为2米,宽为1米的大门,对角线大约是______米(精确到0.01).
五、课堂小结
1.什么叫无理数?
2.有理数与无理数的区别是什么?
六、达标测试
1.下列数中是无理数的是( )
A.0.12 B. C.0 D.
2.下列说法中正确的是( )
A.不循环小数是无理数B.分数不是有理数C.有理数都是有限小数D.3.1415926是有理数
3.下列语句正确的是( )
A.3.78788788878888是无理数 B.无理数分正无理数、零、负无理数
C.无限小数不能化成分数 D.无限不循环小数是无理数
4、已知:在数-,-,π,3.1416,,0,42,(-1)2n,-1.424224222…中,
(1)写出所有有理数;
(2)写出所有无理数;
(3)把这些数按由小到大的顺序排列起来,并用符号“<”连接.
学习目标:
1、 借助计算器探索无理数是无限不循环小数。
2、 会判断一个数是无理数还是有理数。
重点:理解无理数的认识。
难点:会判断一个数是无理数还是有理数,有理数与无理数的区别。
学习过程
一、知识衔接
面积为2的正方形的边长究竟为多少呢?
二、探究新知
1、(1)上图3个正方形的边长之间有怎样的大小关系?
(2)边长a的整数部分是几?十分位是几?百分位是几?千分位等
(3)整理出的表格。
边长a 面积S
还能往下算吗?可能是有限小数吗?
结论:所以a不可能是 小数。它是一个 小数。
2、估计面积为5的正方形的边长的值,(结果精确到十分位)并用计算器检验。
2.的结果精确到百分位呢?结果精确到千分位呢?
归纳:事实上,b= 也是一个 小数。
3、同样,对于体积为2的正方体,借助计算器,可以得到它的棱长 ,它也是一个 小数。
三、精讲点拨
1、把下面各数表示成小数,你发现了什么?
3,,,,,。
共识:有理数总可以用 小数表示,反过来,任何 小数也都是有理数。
总结:无限不循环小数叫做无理数。
除了象上面的,,是无理数外,像我们熟悉的圆周率也是一个无限不循环小数,所以它也是无理数。
再如:(相邻两个5之间8的个数逐次增1)也是无理数。
四、随堂练习
1、下列各数中,哪些是有理数?哪些是无理数?
,,………,…(相邻两个1之间0的个数逐渐加1)。
2、判断下列说法是否正确:
(1)有限小数是有理数; ( )(2)无限小数都是无理数; ( )
(3)无理数都是无限小数; ( )(4)有理数是有限数. ( )
3、在0.351,-,4.969696…,6.751755175551…,0,-5.2333,5.411010010001…中,无理数的个数有______.
4、面积为6的长方形,长是宽的2倍,则宽为( )21世纪教育网
A.小数 B.分数 C.无理数 D.不能确定21世纪教育网
5、面积为3的正方形的边长______有理数;面积为4的正方形的边长______有理数.(填“是”或“不是”)
6、一个高为2米,宽为1米的大门,对角线大约是______米(精确到0.01).
五、课堂小结
1.什么叫无理数?
2.有理数与无理数的区别是什么?
六、达标测试
1.下列数中是无理数的是( )
A.0.12 B. C.0 D.
2.下列说法中正确的是( )
A.不循环小数是无理数B.分数不是有理数C.有理数都是有限小数D.3.1415926是有理数
3.下列语句正确的是( )
A.3.78788788878888是无理数 B.无理数分正无理数、零、负无理数
C.无限小数不能化成分数 D.无限不循环小数是无理数
4、已知:在数-,-,π,3.1416,,0,42,(-1)2n,-1.424224222…中,
(1)写出所有有理数;
(2)写出所有无理数;
(3)把这些数按由小到大的顺序排列起来,并用符号“<”连接.
