苏教版(2019)高中数学必修第二册 13.3.1空间图形的表面积 教学设计
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 13.3.1空间图形的表面积 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 501.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 09:37:20 | ||
图片预览



文档简介
第十三章 立体几何初步
13.3 空间图形的表面积和体积
13.3.1 空间图形的表面积
《课程标准》指出:几何学是研究现实世界中物体的形状、大小与位置关系的数学学科.人们通常采用直观感知、操作确认、思辨论证、度量计算等方法认识和探索几何图形及其性质.三维空间是人类生存的现实空间,认识空间图形,培养和发展学生的空间想像能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力,是高中阶段数学必修系列课程的基本要求.在《立体几何初步》部分,学生将先从对空间几何体的整体观察入手,认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系;能用数学语言表述有关平行、垂直的性质与判定,并对某些结论进行论证.学生还将了解一些简单几何体的表面积与体积的计算方法.
课程目标 学科素养
1.通过对柱体、锥体、台体的研究,掌握柱体、锥体、台体的表面积的求法. 2.了解柱体、锥体、台体的表面积计算公式;能运用柱体、锥体、台体的表面积公式进行计算和解决有关实际问题. 3.培养空间想象能力和思维能力. 在计算棱柱、棱锥、棱台的表面积的过程中,要把实际问题转化为数学问题,并进行计算,发展学生的数学建模、数学运算素养和直观想象素养.
1.教学重点:掌握柱体、锥体、台体的表面积的求法.
2.教学难点:能运用柱体、锥体、台体的表面积公式进行计算和解决有关实际问题.
多媒体调试、讲义分发。
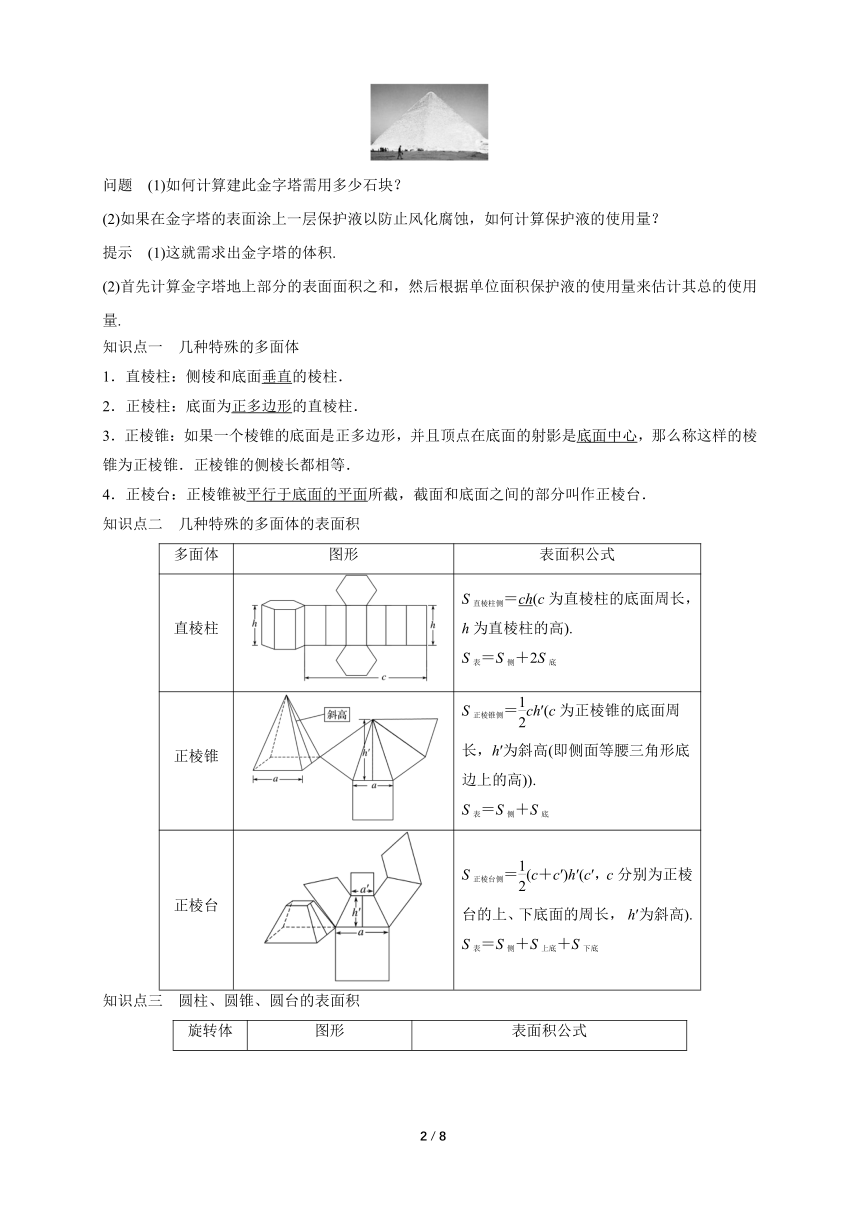
胡夫大金字塔底边原长230米,高146.59米,经风化腐蚀,现降至136.5米,塔的底角为51°51′.假如把建造金字塔的石块凿成平均一立方英尺的小块,平均每块重2.5吨,像一辆小汽车那样大.
问题 (1)如何计算建此金字塔需用多少石块?
(2)如果在金字塔的表面涂上一层保护液以防止风化腐蚀,如何计算保护液的使用量?
提示 (1)这就需求出金字塔的体积.
(2)首先计算金字塔地上部分的表面面积之和,然后根据单位面积保护液的使用量来估计其总的使用量.
知识点一 几种特殊的多面体
1.直棱柱:侧棱和底面垂直的棱柱.
2.正棱柱:底面为正多边形的直棱柱.
3.正棱锥:如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,那么称这样的棱锥为正棱锥.正棱锥的侧棱长都相等.
4.正棱台:正棱锥被平行于底面的平面所截,截面和底面之间的部分叫作正棱台.
知识点二 几种特殊的多面体的表面积
多面体 图形 表面积公式
直棱柱 S直棱柱侧=ch(c为直棱柱的底面周长,h为直棱柱的高). S表=S侧+2S底
正棱锥 S正棱锥侧=ch′(c为正棱锥的底面周长,h′为斜高(即侧面等腰三角形底边上的高)). S表=S侧+S底
正棱台 S正棱台侧=(c+c′)h′(c′,c分别为正棱台的上、下底面的周长, h′为斜高). S表=S侧+S上底+S下底
知识点三 圆柱、圆锥、圆台的表面积
旋转体 图形 表面积公式
圆柱 底面积:S底=2πr2, 侧面积:S侧=2πrl, 表面积:S=2πr(r+l)
圆锥 底面积:S底=πr2, 侧面积:S侧=πrl, 表面积:S=πr(r+l)
圆台 上底面面积:S上底=πr′2,下底面面积:S下底=πr2,侧面积:S侧=π(r′l+rl),表面积:S=π(r′2+r2+r′l+rl)
一、求多面体的侧面积和表面积
例1 正四棱台两底面边长分别为a和b(a(1)若侧棱所在直线与上、下底面正方形中心的连线所成的角为45°,求棱台的侧面积;
(2)若棱台的侧面积等于两底面面积之和,求它的高.
解 (1)如图所示,设O1,O分别为上、下底面的中心,过C1作C1E⊥AC于E,过E作EF⊥BC于F,连接C1F,则C1F为正四棱台的斜高.
由题意知∠C1CO=45°,
CE=CO-EO=CO-C1O1=(b-a).
在Rt△C1CE中,C1E=CE=(b-a),
又EF=CE·sin 45°=(b-a),
∴C1F=
==(b-a).
∴S侧=(4a+4b)×(b-a)=(b2-a2).
(2)∵S侧=S底,S底=a2+b2,
∴4·(a+b)·h斜=a2+b2,
∴h斜=.
又EF=,∴h==.
延伸探究
若正四棱台的高是12 cm,两底面边长之差为10 cm,表面积为512 cm2,求底面的边长.
解 如图,设上底面边长为x cm,则下底面边长为(x+10)cm,
在Rt△E1FE中,
EF==5(cm).
∵E1F=12 cm,
∴斜高E1E=13 cm.
∴S侧=4×(x+x+10)×13=52(x+5),
S表=52(x+5)+x2+(x+10)2=2x2+72x+360.
∵S表=512 cm2,
∴2x2+72x+360=512,
解得x=-38(舍去)或x=2.
∴x+10=12.
∴正四棱台的上、下底面边长分别为2 cm,12 cm.
反思感悟 (1)求棱锥、棱台及棱柱的侧面积和表面积的关键是求底面边长,高,斜高,侧棱.求解时要注意直角三角形和梯形的应用.
(2)正棱柱、正棱锥、正棱台的所有侧面都全等,因此求侧面积时,可先求一个侧面的面积,然后乘以侧面的个数.
(3)棱台是由棱锥所截得到的,因此棱台的侧面积也可由大小棱锥侧面积作差得到.
跟踪训练1 已知正四棱锥的侧面积是底面积的2倍,高为3,求它的表面积.
解 如图,设PO=3,PE是斜高,
∵S侧=2S底,
∴4··BC·PE=2BC2,
∴BC=PE.
在Rt△POE中,PO=3,OE=BC=PE,
∴9+2=PE2,
∴PE=2.
∴S底=BC2=PE2=(2)2=12,
S侧=2S底=2×12=24,
∴S表=S底+S侧=12+24=36.
二、求旋转体的表面积
例2 圆台的上、下底面半径分别为10 cm和20 cm.它的侧面展开图扇环的圆心角为180°,那么圆台的表面积是________ cm2.(结果中保留π)
答案 1 100π
解析 如图所示,
设圆台的上底面周长为ccm,上、下底面半径分别为r1,r2,
因为扇环的圆心角是180°,
故c=π×SA=2π×10,
所以SA=20 cm.
同理可得SB=40 cm.
所以AB=SB-SA=20(cm),
所以S表=S侧+S上+S下
=π(r1+r2)×AB+πr+πr
=π(10+20)×20+π×102+π×202=1 100π(cm2).
故圆台的表面积为1 100π cm2.
延伸探究
若本例条件改为:圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,求圆台较小底面的半径.
解 设圆台较小底面的半径为r,
则另一底面半径为3r,由题意知母线长l=3,
∵S侧=π(r+3r)×3=84π,∴r=7.
反思感悟 (1)求圆柱、圆锥和圆台的侧面积和表面积,只需求出上、下底面半径和母线长即可,求半径和母线长时常借助轴截面.
(2)解答旋转体的侧面积与表面积问题可先把空间问题转化为平面问题,即在展开图内求母线的长,再进一步代入侧面积公式求出侧面积,进而求出表面积.
(3)旋转体的轴截面是化空间问题为平面问题的重要工具,因为在轴截面中集中体现了旋转体的“关键量”之间的关系.在推导这些量之间的关系时要注意比例性质的应用.
跟踪训练2 如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,AB=5 cm,BC=16 cm,AD=4 cm,求以AB所在直线为轴旋转一周所得空间图形的表面积.
解 以AB所在直线为轴旋转一周所得空间图形是圆台,
其上底面半径是4 cm,下底面半径是16 cm,
母线DC==13(cm),
所以该空间图形的表面积为π(4+16)×13+π×42+π×162=532π(cm2).
三、简单组合体的表面积
例3 牧民居住的蒙古包的形状是一个圆柱与圆锥的组合体,尺寸如图所示(单位:m),请你帮助算出要搭建这样的一个蒙古包至少需要多少篷布?(精确到0.01 m2,π取3.14)
解 上部分圆锥体的母线长为 m,其侧面积为S1=π××(m2).
下部分圆柱体的侧面积为S2=π×5×1.8(m2).
∴搭建这样的一个蒙古包至少需要的篷布为
S=S1+S2=π××+π×5×1.8
≈50.03(m2).
反思感悟 (1)组合体的侧面积和表面积问题,首先要弄清楚它由哪些简单空间图形组成,然后再根据条件求各个简单组合体的基本量,注意方程思想的应用.
(2)在实际问题中,常通过计算物体的表面积来研究如何合理地用料,如何节省原材料等,在求解时应结合实际,明确实际物体究竟是哪种空间图形,哪些面计算在内,哪些面在实际中没有.
跟踪训练3 如图所示的空间图形是一棱长为4 cm的正方体,若在其中一个面的中心位置上,挖一个直径为2 cm、深为1 cm的圆柱形的洞,求挖洞后空间图形的表面积是多少?(π取3.14)
解 因为正方体的棱长为4 cm,而洞深只有1 cm,所以正方体没有被打透,这样一来打洞后所得空间图形的表面积等于原来正方体的表面积,再加上圆柱的侧面积,这个圆柱的高为1 cm,底面圆的半径为1 cm.
正方体的表面积为4×4×6=96(cm2),
圆柱的侧面积为2π×1×1≈6.28(cm2),
则挖洞后空间图形的表面积约为96+6.28=102.28(cm2).
1.若圆锥的底面半径为1,高为,则圆锥的表面积为( )
A.π B.2π
C.3π D.4π
答案 C
解析 设圆锥的母线长为l,则l==2,所以圆锥的表面积为S=π×1×(1+2)=3π.
2.已知正四棱锥的底面边长为6,侧棱长为5,则此棱锥的侧面积为( )
A.6 B.12 C.24 D.48
答案 D
解析 正四棱锥的斜高h′==4,S侧=4××6×4=48.
3.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12π B.12π C.8π D.10π
答案 B
解析 因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为2,底面圆的直径为2,所以该圆柱的表面积为2×π×()2+2π××2=12π.
4.已知一个圆台的母线长等于上、下底面半径和的一半,且侧面积是32π,则母线长为________.
答案 4
解析 ∵l=,
∴S侧=π(R+r)l=2πl2=32π,
∴l=4.
5.已知一个正四棱柱的对角线的长是9 cm,表面积等于144 cm2,则这个棱柱的侧面积为________ cm2.
答案 112或72
解析 设底面边长、侧棱长分别为a cm,l cm,
则
解得或
∴S侧=4×4×7=112(cm2)或S侧=4×6×3=72 (cm2).
应从学生熟悉的正方体、长方体的侧面展开图入手探究展开图和表面积的关系.
2 / 2
13.3 空间图形的表面积和体积
13.3.1 空间图形的表面积
《课程标准》指出:几何学是研究现实世界中物体的形状、大小与位置关系的数学学科.人们通常采用直观感知、操作确认、思辨论证、度量计算等方法认识和探索几何图形及其性质.三维空间是人类生存的现实空间,认识空间图形,培养和发展学生的空间想像能力、推理论证能力、运用图形语言进行交流的能力以及几何直观能力,是高中阶段数学必修系列课程的基本要求.在《立体几何初步》部分,学生将先从对空间几何体的整体观察入手,认识空间图形;再以长方体为载体,直观认识和理解空间点、线、面的位置关系;能用数学语言表述有关平行、垂直的性质与判定,并对某些结论进行论证.学生还将了解一些简单几何体的表面积与体积的计算方法.
课程目标 学科素养
1.通过对柱体、锥体、台体的研究,掌握柱体、锥体、台体的表面积的求法. 2.了解柱体、锥体、台体的表面积计算公式;能运用柱体、锥体、台体的表面积公式进行计算和解决有关实际问题. 3.培养空间想象能力和思维能力. 在计算棱柱、棱锥、棱台的表面积的过程中,要把实际问题转化为数学问题,并进行计算,发展学生的数学建模、数学运算素养和直观想象素养.
1.教学重点:掌握柱体、锥体、台体的表面积的求法.
2.教学难点:能运用柱体、锥体、台体的表面积公式进行计算和解决有关实际问题.
多媒体调试、讲义分发。
胡夫大金字塔底边原长230米,高146.59米,经风化腐蚀,现降至136.5米,塔的底角为51°51′.假如把建造金字塔的石块凿成平均一立方英尺的小块,平均每块重2.5吨,像一辆小汽车那样大.
问题 (1)如何计算建此金字塔需用多少石块?
(2)如果在金字塔的表面涂上一层保护液以防止风化腐蚀,如何计算保护液的使用量?
提示 (1)这就需求出金字塔的体积.
(2)首先计算金字塔地上部分的表面面积之和,然后根据单位面积保护液的使用量来估计其总的使用量.
知识点一 几种特殊的多面体
1.直棱柱:侧棱和底面垂直的棱柱.
2.正棱柱:底面为正多边形的直棱柱.
3.正棱锥:如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,那么称这样的棱锥为正棱锥.正棱锥的侧棱长都相等.
4.正棱台:正棱锥被平行于底面的平面所截,截面和底面之间的部分叫作正棱台.
知识点二 几种特殊的多面体的表面积
多面体 图形 表面积公式
直棱柱 S直棱柱侧=ch(c为直棱柱的底面周长,h为直棱柱的高). S表=S侧+2S底
正棱锥 S正棱锥侧=ch′(c为正棱锥的底面周长,h′为斜高(即侧面等腰三角形底边上的高)). S表=S侧+S底
正棱台 S正棱台侧=(c+c′)h′(c′,c分别为正棱台的上、下底面的周长, h′为斜高). S表=S侧+S上底+S下底
知识点三 圆柱、圆锥、圆台的表面积
旋转体 图形 表面积公式
圆柱 底面积:S底=2πr2, 侧面积:S侧=2πrl, 表面积:S=2πr(r+l)
圆锥 底面积:S底=πr2, 侧面积:S侧=πrl, 表面积:S=πr(r+l)
圆台 上底面面积:S上底=πr′2,下底面面积:S下底=πr2,侧面积:S侧=π(r′l+rl),表面积:S=π(r′2+r2+r′l+rl)
一、求多面体的侧面积和表面积
例1 正四棱台两底面边长分别为a和b(a
(2)若棱台的侧面积等于两底面面积之和,求它的高.
解 (1)如图所示,设O1,O分别为上、下底面的中心,过C1作C1E⊥AC于E,过E作EF⊥BC于F,连接C1F,则C1F为正四棱台的斜高.
由题意知∠C1CO=45°,
CE=CO-EO=CO-C1O1=(b-a).
在Rt△C1CE中,C1E=CE=(b-a),
又EF=CE·sin 45°=(b-a),
∴C1F=
==(b-a).
∴S侧=(4a+4b)×(b-a)=(b2-a2).
(2)∵S侧=S底,S底=a2+b2,
∴4·(a+b)·h斜=a2+b2,
∴h斜=.
又EF=,∴h==.
延伸探究
若正四棱台的高是12 cm,两底面边长之差为10 cm,表面积为512 cm2,求底面的边长.
解 如图,设上底面边长为x cm,则下底面边长为(x+10)cm,
在Rt△E1FE中,
EF==5(cm).
∵E1F=12 cm,
∴斜高E1E=13 cm.
∴S侧=4×(x+x+10)×13=52(x+5),
S表=52(x+5)+x2+(x+10)2=2x2+72x+360.
∵S表=512 cm2,
∴2x2+72x+360=512,
解得x=-38(舍去)或x=2.
∴x+10=12.
∴正四棱台的上、下底面边长分别为2 cm,12 cm.
反思感悟 (1)求棱锥、棱台及棱柱的侧面积和表面积的关键是求底面边长,高,斜高,侧棱.求解时要注意直角三角形和梯形的应用.
(2)正棱柱、正棱锥、正棱台的所有侧面都全等,因此求侧面积时,可先求一个侧面的面积,然后乘以侧面的个数.
(3)棱台是由棱锥所截得到的,因此棱台的侧面积也可由大小棱锥侧面积作差得到.
跟踪训练1 已知正四棱锥的侧面积是底面积的2倍,高为3,求它的表面积.
解 如图,设PO=3,PE是斜高,
∵S侧=2S底,
∴4··BC·PE=2BC2,
∴BC=PE.
在Rt△POE中,PO=3,OE=BC=PE,
∴9+2=PE2,
∴PE=2.
∴S底=BC2=PE2=(2)2=12,
S侧=2S底=2×12=24,
∴S表=S底+S侧=12+24=36.
二、求旋转体的表面积
例2 圆台的上、下底面半径分别为10 cm和20 cm.它的侧面展开图扇环的圆心角为180°,那么圆台的表面积是________ cm2.(结果中保留π)
答案 1 100π
解析 如图所示,
设圆台的上底面周长为ccm,上、下底面半径分别为r1,r2,
因为扇环的圆心角是180°,
故c=π×SA=2π×10,
所以SA=20 cm.
同理可得SB=40 cm.
所以AB=SB-SA=20(cm),
所以S表=S侧+S上+S下
=π(r1+r2)×AB+πr+πr
=π(10+20)×20+π×102+π×202=1 100π(cm2).
故圆台的表面积为1 100π cm2.
延伸探究
若本例条件改为:圆台的一个底面周长是另一个底面周长的3倍,母线长为3,圆台的侧面积为84π,求圆台较小底面的半径.
解 设圆台较小底面的半径为r,
则另一底面半径为3r,由题意知母线长l=3,
∵S侧=π(r+3r)×3=84π,∴r=7.
反思感悟 (1)求圆柱、圆锥和圆台的侧面积和表面积,只需求出上、下底面半径和母线长即可,求半径和母线长时常借助轴截面.
(2)解答旋转体的侧面积与表面积问题可先把空间问题转化为平面问题,即在展开图内求母线的长,再进一步代入侧面积公式求出侧面积,进而求出表面积.
(3)旋转体的轴截面是化空间问题为平面问题的重要工具,因为在轴截面中集中体现了旋转体的“关键量”之间的关系.在推导这些量之间的关系时要注意比例性质的应用.
跟踪训练2 如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,AB=5 cm,BC=16 cm,AD=4 cm,求以AB所在直线为轴旋转一周所得空间图形的表面积.
解 以AB所在直线为轴旋转一周所得空间图形是圆台,
其上底面半径是4 cm,下底面半径是16 cm,
母线DC==13(cm),
所以该空间图形的表面积为π(4+16)×13+π×42+π×162=532π(cm2).
三、简单组合体的表面积
例3 牧民居住的蒙古包的形状是一个圆柱与圆锥的组合体,尺寸如图所示(单位:m),请你帮助算出要搭建这样的一个蒙古包至少需要多少篷布?(精确到0.01 m2,π取3.14)
解 上部分圆锥体的母线长为 m,其侧面积为S1=π××(m2).
下部分圆柱体的侧面积为S2=π×5×1.8(m2).
∴搭建这样的一个蒙古包至少需要的篷布为
S=S1+S2=π××+π×5×1.8
≈50.03(m2).
反思感悟 (1)组合体的侧面积和表面积问题,首先要弄清楚它由哪些简单空间图形组成,然后再根据条件求各个简单组合体的基本量,注意方程思想的应用.
(2)在实际问题中,常通过计算物体的表面积来研究如何合理地用料,如何节省原材料等,在求解时应结合实际,明确实际物体究竟是哪种空间图形,哪些面计算在内,哪些面在实际中没有.
跟踪训练3 如图所示的空间图形是一棱长为4 cm的正方体,若在其中一个面的中心位置上,挖一个直径为2 cm、深为1 cm的圆柱形的洞,求挖洞后空间图形的表面积是多少?(π取3.14)
解 因为正方体的棱长为4 cm,而洞深只有1 cm,所以正方体没有被打透,这样一来打洞后所得空间图形的表面积等于原来正方体的表面积,再加上圆柱的侧面积,这个圆柱的高为1 cm,底面圆的半径为1 cm.
正方体的表面积为4×4×6=96(cm2),
圆柱的侧面积为2π×1×1≈6.28(cm2),
则挖洞后空间图形的表面积约为96+6.28=102.28(cm2).
1.若圆锥的底面半径为1,高为,则圆锥的表面积为( )
A.π B.2π
C.3π D.4π
答案 C
解析 设圆锥的母线长为l,则l==2,所以圆锥的表面积为S=π×1×(1+2)=3π.
2.已知正四棱锥的底面边长为6,侧棱长为5,则此棱锥的侧面积为( )
A.6 B.12 C.24 D.48
答案 D
解析 正四棱锥的斜高h′==4,S侧=4××6×4=48.
3.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( )
A.12π B.12π C.8π D.10π
答案 B
解析 因为过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,所以圆柱的高为2,底面圆的直径为2,所以该圆柱的表面积为2×π×()2+2π××2=12π.
4.已知一个圆台的母线长等于上、下底面半径和的一半,且侧面积是32π,则母线长为________.
答案 4
解析 ∵l=,
∴S侧=π(R+r)l=2πl2=32π,
∴l=4.
5.已知一个正四棱柱的对角线的长是9 cm,表面积等于144 cm2,则这个棱柱的侧面积为________ cm2.
答案 112或72
解析 设底面边长、侧棱长分别为a cm,l cm,
则
解得或
∴S侧=4×4×7=112(cm2)或S侧=4×6×3=72 (cm2).
应从学生熟悉的正方体、长方体的侧面展开图入手探究展开图和表面积的关系.
2 / 2
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
