苏教版(2019)高中数学必修第二册13.3.2空间图形的体积练习(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册13.3.2空间图形的体积练习(解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 281.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 09:39:11 | ||
图片预览



文档简介
13.3 空间图形的表面积和体积
13.3.2 空间图形的体积
1.直径为6的球的表面积和体积分别是( )
A.144π,144π B.144π,36π
C.36π,144π D.36π,36π
2.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.58 D.58π
3.如图所示,在正方体ABCD-A1B1C1D1中,四棱锥S-ABCD的体积占正方体体积的( )
A. B.
C. D.不确定
4.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的空间图形的体积为( )
A. B. C.2π D.4π
5.若一个圆台如图所示,则其体积等于( )
A.3π B.3
C. D.
6.已知三个球的表面积之比是1∶2∶3,则这三个球的体积之比为________.
7.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为______.
8.一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则圆柱和圆锥的表面积之比为________,其体积之比为________.
9.在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E-ABCD的体积为V,那么三棱锥M-EBC的体积为多少?
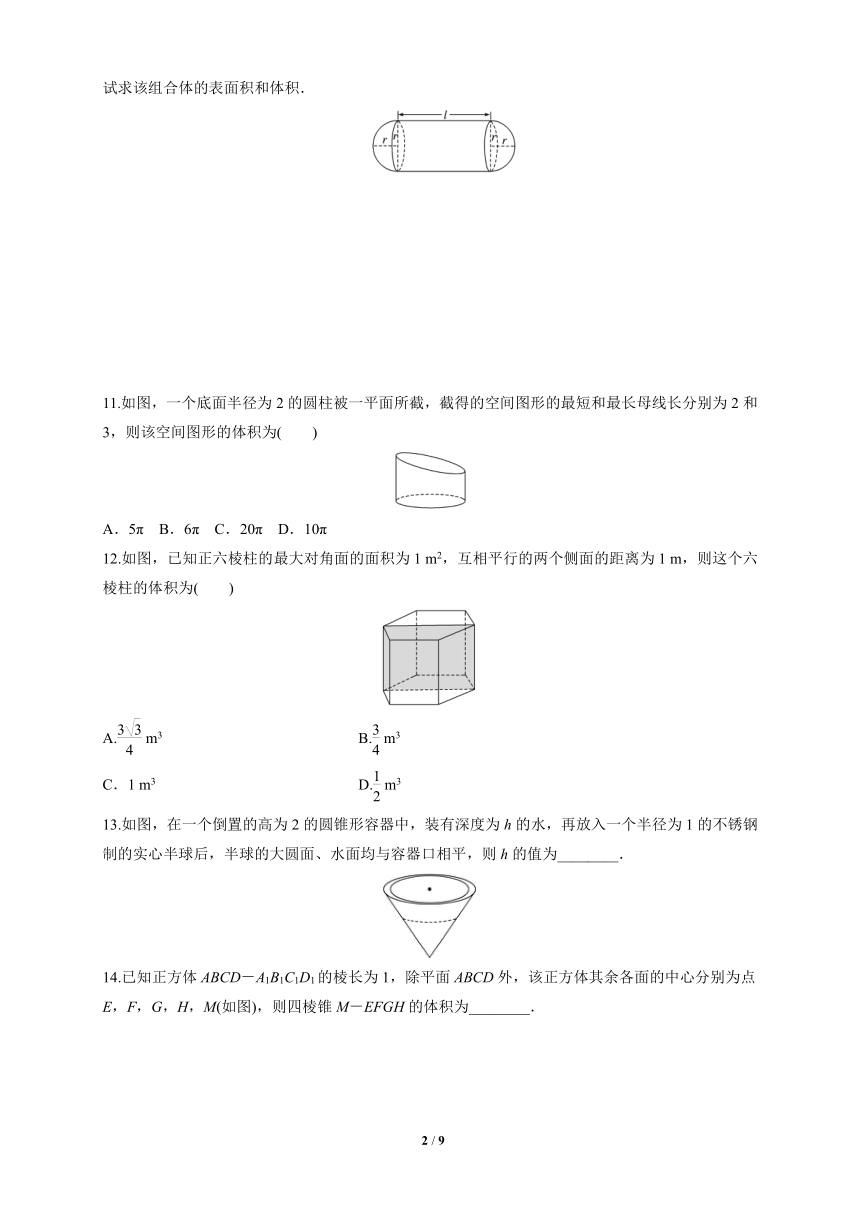
10.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
11.如图,一个底面半径为2的圆柱被一平面所截,截得的空间图形的最短和最长母线长分别为2和3,则该空间图形的体积为( )
A.5π B.6π C.20π D.10π
12.如图,已知正六棱柱的最大对角面的面积为1 m2,互相平行的两个侧面的距离为1 m,则这个六棱柱的体积为( )
A. m3 B. m3
C.1 m3 D. m3
13.如图,在一个倒置的高为2的圆锥形容器中,装有深度为h的水,再放入一个半径为1的不锈钢制的实心半球后,半球的大圆面、水面均与容器口相平,则h的值为________.
14.已知正方体ABCD-A1B1C1D1的棱长为1,除平面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为________.
15.(多选)用平行于棱锥底面的平面去截棱锥,得到上、下两部分空间图形且上、下两部分的高之比为1∶2,则关于上、下两空间图形的说法正确的是( )
A.侧面积之比为1∶4 B.侧面积之比为1∶8
C.体积之比为1∶27 D.体积之比为1∶26
16.如图所示,一个圆锥形的空杯子上放着一个直径为8 cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?材料最省为多少?
\
13.3 空间图形的表面积和体积
13.3.2 空间图形的体积答案
1.直径为6的球的表面积和体积分别是( )
A.144π,144π B.144π,36π
C.36π,144π D.36π,36π
【答案】 D
【解析】 半径R=3.所以S表=4πR2=36π,V=πR3=×27=36π.故选D.
2.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.58 D.58π
【答案】 A
【解析】 设上底面半径为r,则由题意求得下底面半径为3r,设圆台高为h1,
则52=πh1(r2+9r2+3r·r),
∴πr2h1=12.令原圆锥的高为h,
由相似知识得=,∴h=h1,
∴V原圆锥=π(3r)2×h=3πr2×h1=×12=54.
3.如图所示,在正方体ABCD-A1B1C1D1中,四棱锥S-ABCD的体积占正方体体积的( )
A. B.
C. D.不确定
【答案】 B
【解析】 令正方体棱长为a,则V正方体=a3,
VS-ABCD=×a2×a=a3,
∴V四棱锥S-ABCD=V正方体.
4.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的空间图形的体积为( )
A. B. C.2π D.4π
【答案】 B
【解析】 绕等腰直角三角形的斜边所在的直线旋转一周而形成的曲面围成的空间图形为两个底面重合,等体积的圆锥,如图所示.每一个圆锥的底面半径和高都为,故所求空间图形的体积V=2××2π×=.
5.若一个圆台如图所示,则其体积等于( )
A.3π B.3
C. D.
【答案】 C
【解析】 圆台的上底面面积S=π,下底面面积S′=4π,高h=,
所以V圆台=××(π+4π+2π)=.
6.已知三个球的表面积之比是1∶2∶3,则这三个球的体积之比为________.
【答案】 1∶2∶3
【解析】 设三个球的半径分别为a,b,c,根据球的表面积公式得出4πa2∶4πb2∶4πc2=1∶2∶3,所以它们的半径之比为a∶b∶c=1∶∶.则它们的体积之比是a3∶b3∶c3=1∶2∶3.
7.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为______.
【答案】 1
【解析】 ∵正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,
∴底面B1DC1的面积为×2×=.
三棱锥A-B1DC1的高就是底面正三角形的高.
∴三棱锥A-B1DC1的体积为××=1.
8.一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则圆柱和圆锥的表面积之比为________,其体积之比为________.
【答案】 2∶1 2∶1
【解析】 S圆柱=2·π2+2π··a=a2.
S圆锥=π2+π··a=a2.
∴S圆柱∶S圆锥=2∶1.
V圆柱=π2·a=a3,
V圆锥=·π2·a=a3,
∴V圆柱∶V圆锥=a3∶a3=2∶1.
9.在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E-ABCD的体积为V,那么三棱锥M-EBC的体积为多少?
解 设点B到平面EMC的距离为h1,点D到平面EMC的距离为h2,
连接MD,因为M是AE的中点,
所以VM-ABCD=V,
所以VE-MBC=V-VE-MDC.
而VE-MBC=VB-EMC,VE-MDC=VD-EMC,
所以==.
因为B,D到平面EMC的距离即为到平面EAC的距离,而AB∥CD,且2AB=3CD,
所以=.
所以VE-MBC=VM-EBC=V.
10.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
解 该组合体的表面积S=4πr2+2πrl=4π×12+2π×1×3=10π.
该组合体的体积V=πr3+πr2l
=π×13+π×12×3=.
11.如图,一个底面半径为2的圆柱被一平面所截,截得的空间图形的最短和最长母线长分别为2和3,则该空间图形的体积为( )
A.5π B.6π C.20π D.10π
【答案】 D
【解析】 用一个完全相同的空间图形把题中空间图形补成一个圆柱,如图,则圆柱的体积为π×22×5=20π,故所求几何体的体积为10π.
12.如图,已知正六棱柱的最大对角面的面积为1 m2,互相平行的两个侧面的距离为1 m,则这个六棱柱的体积为( )
A. m3 B. m3
C.1 m3 D. m3
【答案】 B
【解析】 设正六棱柱的底面边长为a m,高为h m,则2ah=1,a=1,解得a=,h=,所以六棱柱的体积V=×2×6×=(m3).
13.如图,在一个倒置的高为2的圆锥形容器中,装有深度为h的水,再放入一个半径为1的不锈钢制的实心半球后,半球的大圆面、水面均与容器口相平,则h的值为________.
【答案】
【解析】 设圆锥的底面半径为r,体积为V,半球的体积为V1,水(小圆锥)的体积为V2,如图.
则OA=r,OC=1,OB=2,BE=h,所以ED=,2×r=×1,解得r2=,
所以V=πr2×2=π,V1=π,V2=π×2×h=πh3,
由V=V1+V2,得π=π+πh3,解得h=.
14.已知正方体ABCD-A1B1C1D1的棱长为1,除平面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为________.
【答案】
【解析】 连接AD1,CD1,B1A,B1C,AC(图略),
∵E,H分别为AD1,CD1的中点,
∴EH∥AC,EH=AC.
∵F,G分别为B1A,B1C的中点,
∴FG∥AC,FG=AC,
∴EH∥FG,EH=FG,∴四边形EHGF为平行四边形,
又EG=HF,EH=HG,∴四边形EHGF为正方形.
又四棱锥M-EFGH的高为,
∴四棱锥M-EFGH的体积为×2×=.
15.(多选)用平行于棱锥底面的平面去截棱锥,得到上、下两部分空间图形且上、下两部分的高之比为1∶2,则关于上、下两空间图形的说法正确的是( )
A.侧面积之比为1∶4 B.侧面积之比为1∶8
C.体积之比为1∶27 D.体积之比为1∶26
【答案】 BD
【解析】 依题意知,上部分为小棱锥,下部分为棱台,
所以小棱锥与原棱锥的底面边长之比为1∶3,高之比为1∶3,
所以小棱锥与原棱锥的侧面积之比为1∶9,体积之比为1∶27,
即小棱锥与棱台的侧面积之比为1∶8,体积之比为1∶26.
16.如图所示,一个圆锥形的空杯子上放着一个直径为8 cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?材料最省为多少?
解 要使冰淇淋融化后不会溢出杯子,
则必须有V圆锥≥V半球,
而V半球=××43,V圆锥=π×42×h,
则有π×42×h≥××43,解得h≥8,
即当圆锥形杯子的高大于或等于8 cm时,冰淇淋融化后不会溢出杯子.
又因为S圆锥侧=4π,
所以当高为8 cm时,制作的杯子最省材料,材料最省为16π cm2.
2 / 2
13.3.2 空间图形的体积
1.直径为6的球的表面积和体积分别是( )
A.144π,144π B.144π,36π
C.36π,144π D.36π,36π
2.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.58 D.58π
3.如图所示,在正方体ABCD-A1B1C1D1中,四棱锥S-ABCD的体积占正方体体积的( )
A. B.
C. D.不确定
4.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的空间图形的体积为( )
A. B. C.2π D.4π
5.若一个圆台如图所示,则其体积等于( )
A.3π B.3
C. D.
6.已知三个球的表面积之比是1∶2∶3,则这三个球的体积之比为________.
7.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为______.
8.一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则圆柱和圆锥的表面积之比为________,其体积之比为________.
9.在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E-ABCD的体积为V,那么三棱锥M-EBC的体积为多少?
10.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
11.如图,一个底面半径为2的圆柱被一平面所截,截得的空间图形的最短和最长母线长分别为2和3,则该空间图形的体积为( )
A.5π B.6π C.20π D.10π
12.如图,已知正六棱柱的最大对角面的面积为1 m2,互相平行的两个侧面的距离为1 m,则这个六棱柱的体积为( )
A. m3 B. m3
C.1 m3 D. m3
13.如图,在一个倒置的高为2的圆锥形容器中,装有深度为h的水,再放入一个半径为1的不锈钢制的实心半球后,半球的大圆面、水面均与容器口相平,则h的值为________.
14.已知正方体ABCD-A1B1C1D1的棱长为1,除平面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为________.
15.(多选)用平行于棱锥底面的平面去截棱锥,得到上、下两部分空间图形且上、下两部分的高之比为1∶2,则关于上、下两空间图形的说法正确的是( )
A.侧面积之比为1∶4 B.侧面积之比为1∶8
C.体积之比为1∶27 D.体积之比为1∶26
16.如图所示,一个圆锥形的空杯子上放着一个直径为8 cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?材料最省为多少?
\
13.3 空间图形的表面积和体积
13.3.2 空间图形的体积答案
1.直径为6的球的表面积和体积分别是( )
A.144π,144π B.144π,36π
C.36π,144π D.36π,36π
【答案】 D
【解析】 半径R=3.所以S表=4πR2=36π,V=πR3=×27=36π.故选D.
2.体积为52的圆台,一个底面积是另一个底面积的9倍,那么截得这个圆台的圆锥的体积是( )
A.54 B.54π C.58 D.58π
【答案】 A
【解析】 设上底面半径为r,则由题意求得下底面半径为3r,设圆台高为h1,
则52=πh1(r2+9r2+3r·r),
∴πr2h1=12.令原圆锥的高为h,
由相似知识得=,∴h=h1,
∴V原圆锥=π(3r)2×h=3πr2×h1=×12=54.
3.如图所示,在正方体ABCD-A1B1C1D1中,四棱锥S-ABCD的体积占正方体体积的( )
A. B.
C. D.不确定
【答案】 B
【解析】 令正方体棱长为a,则V正方体=a3,
VS-ABCD=×a2×a=a3,
∴V四棱锥S-ABCD=V正方体.
4.已知等腰直角三角形的直角边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的空间图形的体积为( )
A. B. C.2π D.4π
【答案】 B
【解析】 绕等腰直角三角形的斜边所在的直线旋转一周而形成的曲面围成的空间图形为两个底面重合,等体积的圆锥,如图所示.每一个圆锥的底面半径和高都为,故所求空间图形的体积V=2××2π×=.
5.若一个圆台如图所示,则其体积等于( )
A.3π B.3
C. D.
【答案】 C
【解析】 圆台的上底面面积S=π,下底面面积S′=4π,高h=,
所以V圆台=××(π+4π+2π)=.
6.已知三个球的表面积之比是1∶2∶3,则这三个球的体积之比为________.
【答案】 1∶2∶3
【解析】 设三个球的半径分别为a,b,c,根据球的表面积公式得出4πa2∶4πb2∶4πc2=1∶2∶3,所以它们的半径之比为a∶b∶c=1∶∶.则它们的体积之比是a3∶b3∶c3=1∶2∶3.
7.正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,则三棱锥A-B1DC1的体积为______.
【答案】 1
【解析】 ∵正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为,D为BC的中点,
∴底面B1DC1的面积为×2×=.
三棱锥A-B1DC1的高就是底面正三角形的高.
∴三棱锥A-B1DC1的体积为××=1.
8.一个圆柱和一个圆锥的轴截面分别是边长为a的正方形和正三角形,则圆柱和圆锥的表面积之比为________,其体积之比为________.
【答案】 2∶1 2∶1
【解析】 S圆柱=2·π2+2π··a=a2.
S圆锥=π2+π··a=a2.
∴S圆柱∶S圆锥=2∶1.
V圆柱=π2·a=a3,
V圆锥=·π2·a=a3,
∴V圆柱∶V圆锥=a3∶a3=2∶1.
9.在四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,2AB=3CD,M为AE的中点,设E-ABCD的体积为V,那么三棱锥M-EBC的体积为多少?
解 设点B到平面EMC的距离为h1,点D到平面EMC的距离为h2,
连接MD,因为M是AE的中点,
所以VM-ABCD=V,
所以VE-MBC=V-VE-MDC.
而VE-MBC=VB-EMC,VE-MDC=VD-EMC,
所以==.
因为B,D到平面EMC的距离即为到平面EAC的距离,而AB∥CD,且2AB=3CD,
所以=.
所以VE-MBC=VM-EBC=V.
10.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r=1,l=3,试求该组合体的表面积和体积.
解 该组合体的表面积S=4πr2+2πrl=4π×12+2π×1×3=10π.
该组合体的体积V=πr3+πr2l
=π×13+π×12×3=.
11.如图,一个底面半径为2的圆柱被一平面所截,截得的空间图形的最短和最长母线长分别为2和3,则该空间图形的体积为( )
A.5π B.6π C.20π D.10π
【答案】 D
【解析】 用一个完全相同的空间图形把题中空间图形补成一个圆柱,如图,则圆柱的体积为π×22×5=20π,故所求几何体的体积为10π.
12.如图,已知正六棱柱的最大对角面的面积为1 m2,互相平行的两个侧面的距离为1 m,则这个六棱柱的体积为( )
A. m3 B. m3
C.1 m3 D. m3
【答案】 B
【解析】 设正六棱柱的底面边长为a m,高为h m,则2ah=1,a=1,解得a=,h=,所以六棱柱的体积V=×2×6×=(m3).
13.如图,在一个倒置的高为2的圆锥形容器中,装有深度为h的水,再放入一个半径为1的不锈钢制的实心半球后,半球的大圆面、水面均与容器口相平,则h的值为________.
【答案】
【解析】 设圆锥的底面半径为r,体积为V,半球的体积为V1,水(小圆锥)的体积为V2,如图.
则OA=r,OC=1,OB=2,BE=h,所以ED=,2×r=×1,解得r2=,
所以V=πr2×2=π,V1=π,V2=π×2×h=πh3,
由V=V1+V2,得π=π+πh3,解得h=.
14.已知正方体ABCD-A1B1C1D1的棱长为1,除平面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为________.
【答案】
【解析】 连接AD1,CD1,B1A,B1C,AC(图略),
∵E,H分别为AD1,CD1的中点,
∴EH∥AC,EH=AC.
∵F,G分别为B1A,B1C的中点,
∴FG∥AC,FG=AC,
∴EH∥FG,EH=FG,∴四边形EHGF为平行四边形,
又EG=HF,EH=HG,∴四边形EHGF为正方形.
又四棱锥M-EFGH的高为,
∴四棱锥M-EFGH的体积为×2×=.
15.(多选)用平行于棱锥底面的平面去截棱锥,得到上、下两部分空间图形且上、下两部分的高之比为1∶2,则关于上、下两空间图形的说法正确的是( )
A.侧面积之比为1∶4 B.侧面积之比为1∶8
C.体积之比为1∶27 D.体积之比为1∶26
【答案】 BD
【解析】 依题意知,上部分为小棱锥,下部分为棱台,
所以小棱锥与原棱锥的底面边长之比为1∶3,高之比为1∶3,
所以小棱锥与原棱锥的侧面积之比为1∶9,体积之比为1∶27,
即小棱锥与棱台的侧面积之比为1∶8,体积之比为1∶26.
16.如图所示,一个圆锥形的空杯子上放着一个直径为8 cm的半球形的冰淇淋,请你设计一种这样的圆锥形杯子(杯口直径等于半球形的冰淇淋的直径,杯子壁厚忽略不计),使冰淇淋融化后不会溢出杯子,怎样设计最省材料?材料最省为多少?
解 要使冰淇淋融化后不会溢出杯子,
则必须有V圆锥≥V半球,
而V半球=××43,V圆锥=π×42×h,
则有π×42×h≥××43,解得h≥8,
即当圆锥形杯子的高大于或等于8 cm时,冰淇淋融化后不会溢出杯子.
又因为S圆锥侧=4π,
所以当高为8 cm时,制作的杯子最省材料,材料最省为16π cm2.
2 / 2
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
