人教版数学五年级上册 梯形的面积 课件(共18张PPT)
文档属性
| 名称 | 人教版数学五年级上册 梯形的面积 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-16 18:34:51 | ||
图片预览


文档简介
(共18张PPT)
第6单元 多边形的面积
第5课时 梯形的面积(1)
课堂导入
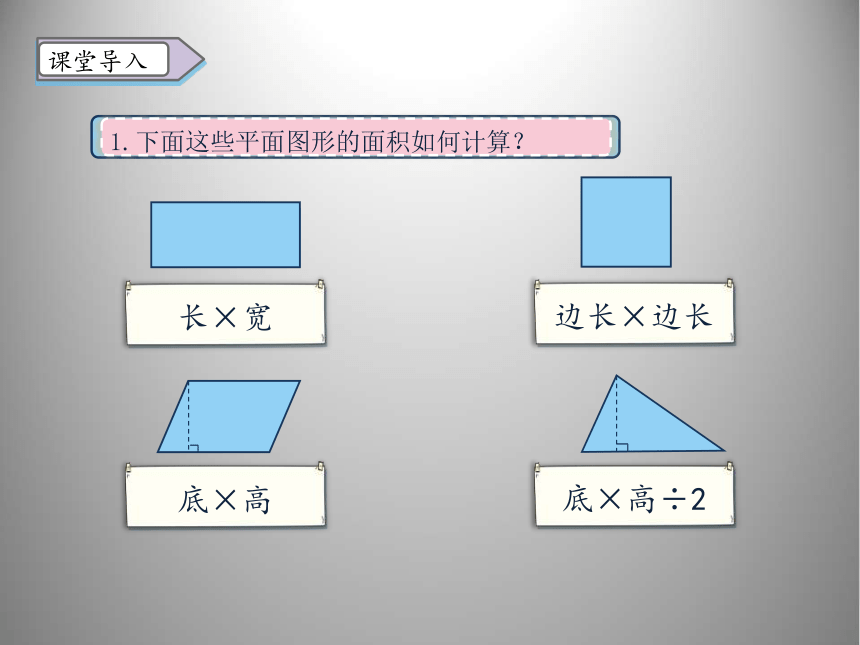
1.下面这些平面图形的面积如何计算?
长×宽
底×高
边长×边长
底×高÷2
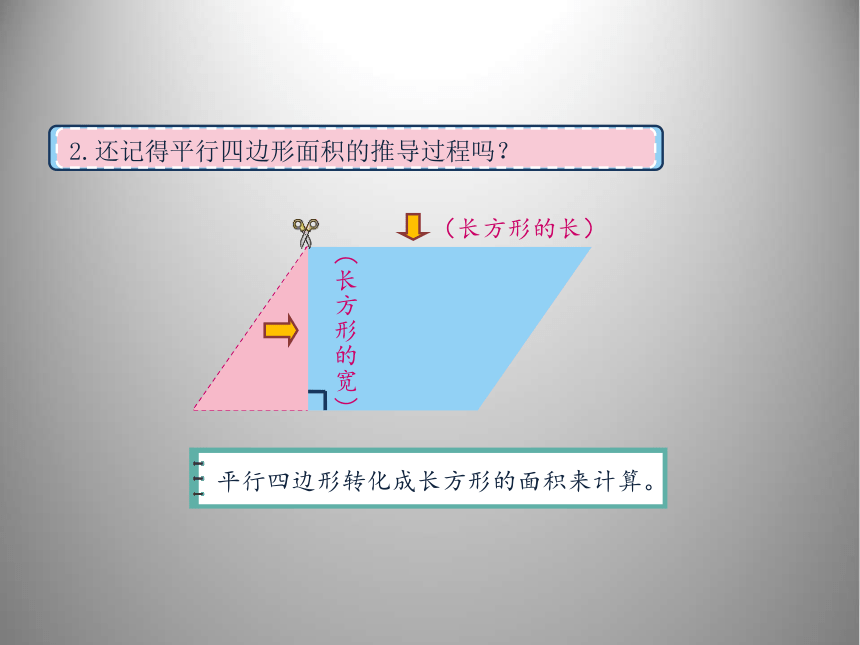
(长方形的长)
(长方形的宽)
2.还记得平行四边形面积的推导过程吗?
平行四边形转化成长方形的面积来计算。
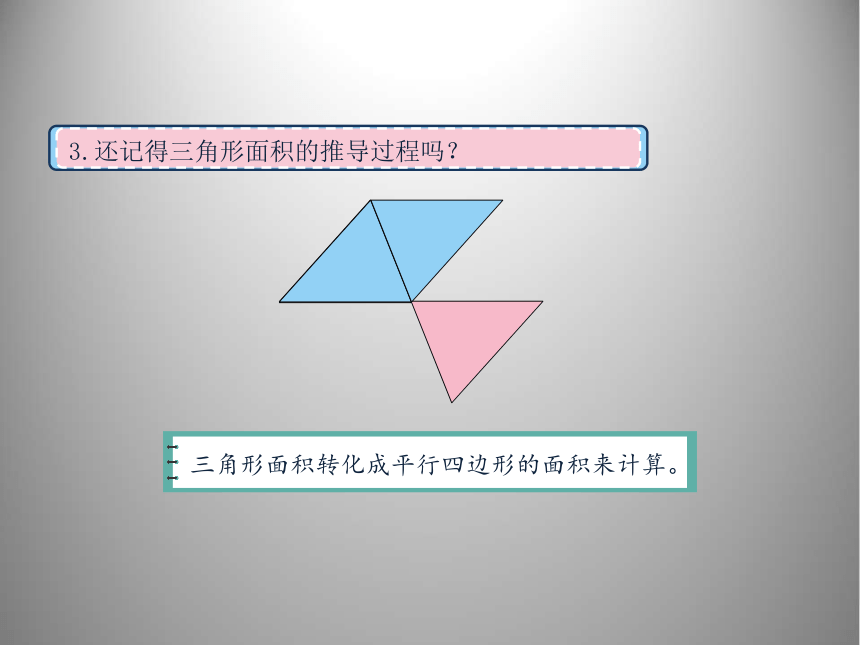
3.还记得三角形面积的推导过程吗?
三角形面积转化成平行四边形的面积来计算。
新知识转化成学过的知识。
转化成学过的图形的面积。
上底
下底
腰
腰
高
4.通过平行四边形、三角形面积的转化过程,给你什么启发?
如何求梯形的面积?
二、探索新知
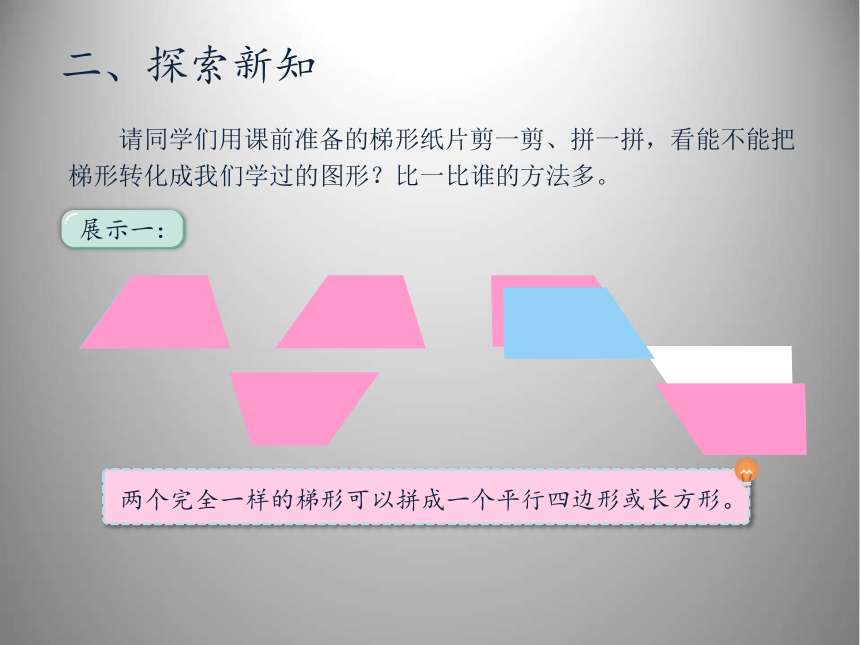
请同学们用课前准备的梯形纸片剪一剪、拼一拼,看能不能把梯形转化成我们学过的图形?比一比谁的方法多。
展示一:
两个完全一样的梯形可以拼成一个平行四边形或长方形。
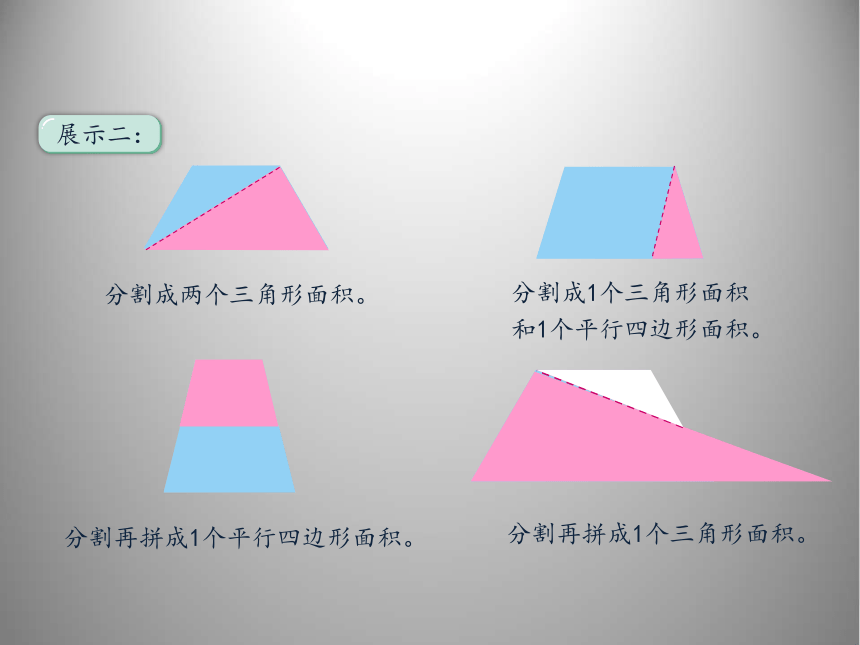
分割成两个三角形面积。
分割成1个三角形面积和1个平行四边形面积。
分割再拼成1个平行四边形面积。
分割再拼成1个三角形面积。
展示二:
说说原来的梯形和转化后图形面积有什么变化?
上底
下底
腰
腰
高
能计算转化后的图形的面积吗?
转化后的图形与原梯形面积相等。
高
上底
下底
下底
上底
梯形面积=平形四边形面积÷2
= ×高÷2
平行四边形的底
(上底+下底)
= ×高÷2
梯形面积=三角形①的面积+三角形②的面积
下底
高
上底
①
②
(上底+下底)
= ×高÷2
=
上底×高÷2
下底×高÷2
+
高
上底
下底
梯形面积 = 平行四边形面积+三角形面积
=
上底×高
(下底-上底)×高÷2
+
梯形面积 =(上底+下底)×高÷2
h
a
b
S =(a+b)×h÷2
= ×高÷2
(上底+下底)
归纳:你觉得求梯形面积的一般公式是什么?
若上底为a,下底为b,高为h,面积S该如何表示?
36 m
120 m
135 m
S =(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 m2 。
做一做
我国三峡水电站大坝的横截面的一部分是梯形(如图),
求它的面积。
(1)两个梯形都能拼成一个平行四边形。 ( )
(2)面积相等的两个梯形,它们的底和高一定分别相等。 ( )
(3)任意一个平行四边形都可以分成两个完全一样的梯形。( )
(4)平行四边形的面积是梯形面积的2倍。 ( )
完全相同两个梯形可以拼成一个平行四边形。
平行四边形的面积是拼成它的梯形面积的2倍。
面积相等的梯形不一定完全相同。
1.判断题
三、应用迁移
40 cm
45 cm
71 cm
65 cm
40 cm
梯形①: S =(a +b)×h÷2
=(40+71)×40÷2
= 2220(cm2)
①
梯形②: S =(a+b)×h÷2
=(45+65)×40÷2
= 2200(cm2)
答:这两块玻璃的面积分别是 2220 cm2和 2200 cm2 。
一辆汽车侧面的两块玻璃是梯形,这两块玻璃的面积分别是多少?
2.
②
四、当堂检测
(2)一个梯形上底是 4 cm ,下底是 10 cm ,高是 6 cm ,这个梯形的面积是( )cm2
(1)两个完全一样的梯形可以拼成一个( ),梯形的上底
与下底的和等于平行四边形的( ),梯形的高等于平行四边
形的( )。所以梯形的面积等于( ),
用字母表示是( )。
平行四边形
底
高
(上底+下底)×高÷2
S =(a +b)×h÷2
42
1.填空。
S =(a +b)×h÷2
=(4+7)×6÷2
=11×6÷2
=33(平方分米)
S =(a +b)×h÷2
=(3.5+6.5)×5÷2
=10×5÷2
=25(平方分米)
3.5
6.5
5
求下面图形的面积。(图中单位:分米)
2.
7
4
6
化单位:4500 m2= 0.45公顷
答:刘大伯至少要准备 72 kg 化肥。
一共要施化肥:0.45×160=72(kg)
梯形面积 =(上底+下底)×高÷2
= (58+92)×60÷2
= 4500(m2)
刘大伯家的一块梯形稻田的上底是 58 m,下底是 92 m,高是 60 m。刘大伯至少要准备多少千克化肥?
3.
每公顷要施化肥 160 kg 。
1.在这节课里你有什么收获?你有什么要提醒大家注意的?
2.今天,你能否运用梯形的面积公式熟练地哪些解决问题?
五、回顾反思
1.完成课本第95页,第5;第96页,第6题。
2.完成课时练第73页,课后练习第1题,第2题。
六、作业布置
第6单元 多边形的面积
第5课时 梯形的面积(1)
课堂导入
1.下面这些平面图形的面积如何计算?
长×宽
底×高
边长×边长
底×高÷2
(长方形的长)
(长方形的宽)
2.还记得平行四边形面积的推导过程吗?
平行四边形转化成长方形的面积来计算。
3.还记得三角形面积的推导过程吗?
三角形面积转化成平行四边形的面积来计算。
新知识转化成学过的知识。
转化成学过的图形的面积。
上底
下底
腰
腰
高
4.通过平行四边形、三角形面积的转化过程,给你什么启发?
如何求梯形的面积?
二、探索新知
请同学们用课前准备的梯形纸片剪一剪、拼一拼,看能不能把梯形转化成我们学过的图形?比一比谁的方法多。
展示一:
两个完全一样的梯形可以拼成一个平行四边形或长方形。
分割成两个三角形面积。
分割成1个三角形面积和1个平行四边形面积。
分割再拼成1个平行四边形面积。
分割再拼成1个三角形面积。
展示二:
说说原来的梯形和转化后图形面积有什么变化?
上底
下底
腰
腰
高
能计算转化后的图形的面积吗?
转化后的图形与原梯形面积相等。
高
上底
下底
下底
上底
梯形面积=平形四边形面积÷2
= ×高÷2
平行四边形的底
(上底+下底)
= ×高÷2
梯形面积=三角形①的面积+三角形②的面积
下底
高
上底
①
②
(上底+下底)
= ×高÷2
=
上底×高÷2
下底×高÷2
+
高
上底
下底
梯形面积 = 平行四边形面积+三角形面积
=
上底×高
(下底-上底)×高÷2
+
梯形面积 =(上底+下底)×高÷2
h
a
b
S =(a+b)×h÷2
= ×高÷2
(上底+下底)
归纳:你觉得求梯形面积的一般公式是什么?
若上底为a,下底为b,高为h,面积S该如何表示?
36 m
120 m
135 m
S =(a+b)h÷2
=(36+120)×135÷2
= 156×135÷2
= 10530(m2)
答:它的面积是 10530 m2 。
做一做
我国三峡水电站大坝的横截面的一部分是梯形(如图),
求它的面积。
(1)两个梯形都能拼成一个平行四边形。 ( )
(2)面积相等的两个梯形,它们的底和高一定分别相等。 ( )
(3)任意一个平行四边形都可以分成两个完全一样的梯形。( )
(4)平行四边形的面积是梯形面积的2倍。 ( )
完全相同两个梯形可以拼成一个平行四边形。
平行四边形的面积是拼成它的梯形面积的2倍。
面积相等的梯形不一定完全相同。
1.判断题
三、应用迁移
40 cm
45 cm
71 cm
65 cm
40 cm
梯形①: S =(a +b)×h÷2
=(40+71)×40÷2
= 2220(cm2)
①
梯形②: S =(a+b)×h÷2
=(45+65)×40÷2
= 2200(cm2)
答:这两块玻璃的面积分别是 2220 cm2和 2200 cm2 。
一辆汽车侧面的两块玻璃是梯形,这两块玻璃的面积分别是多少?
2.
②
四、当堂检测
(2)一个梯形上底是 4 cm ,下底是 10 cm ,高是 6 cm ,这个梯形的面积是( )cm2
(1)两个完全一样的梯形可以拼成一个( ),梯形的上底
与下底的和等于平行四边形的( ),梯形的高等于平行四边
形的( )。所以梯形的面积等于( ),
用字母表示是( )。
平行四边形
底
高
(上底+下底)×高÷2
S =(a +b)×h÷2
42
1.填空。
S =(a +b)×h÷2
=(4+7)×6÷2
=11×6÷2
=33(平方分米)
S =(a +b)×h÷2
=(3.5+6.5)×5÷2
=10×5÷2
=25(平方分米)
3.5
6.5
5
求下面图形的面积。(图中单位:分米)
2.
7
4
6
化单位:4500 m2= 0.45公顷
答:刘大伯至少要准备 72 kg 化肥。
一共要施化肥:0.45×160=72(kg)
梯形面积 =(上底+下底)×高÷2
= (58+92)×60÷2
= 4500(m2)
刘大伯家的一块梯形稻田的上底是 58 m,下底是 92 m,高是 60 m。刘大伯至少要准备多少千克化肥?
3.
每公顷要施化肥 160 kg 。
1.在这节课里你有什么收获?你有什么要提醒大家注意的?
2.今天,你能否运用梯形的面积公式熟练地哪些解决问题?
五、回顾反思
1.完成课本第95页,第5;第96页,第6题。
2.完成课时练第73页,课后练习第1题,第2题。
六、作业布置
