苏教版(2019)高中数学必修第二册 14.2.2分层抽样课件(共28张PPT)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 14.2.2分层抽样课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 687.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 09:50:52 | ||
图片预览








文档简介
(共28张PPT)
苏教版必修第二册
第14章
14.2.2 分层抽样
某市为调查中小学生的近视情况,在全市范围内对小学生、初中生、高中生三个群体抽样,进而了解中小学生的总体情况和三个群体近视情况的差异大小.
问题 1.上述问题中总体有什么特征?
2.采用抽签法合适吗?若不合适,应该用什么方法抽取样本?
提示 1.该总体中,小学生、初中生、高中生三个群体在年龄、体质等方面存在着明显的差异.
2.不合适,若用抽签法,抽取的样本可能集中于某一个群体,不具有代表性.应该用分层随机抽样抽取样本.
情景引入
内
容
索
引
知识梳理
题型探究
检测反馈
1
知识梳理
PART ONE
知识点一 分层抽样
1.分层抽样的定义
一般地,当总体由差异明显的几个部分组成时,为了使样本更客观地反映总体情况,我们常常将总体中的个体按 分成层次比较分明的几个部分,然后按各个部分在总体中 实施抽样,这种抽样方法叫作分层抽样,所分成的各个部分称为“层”.
不同的特点
所占的比
知识梳理
2.分层抽样的特点
(1)适用于总体由差异明显的几部分组成的情况.
(2)按比例确定每层抽取个体的个数.
(3)在每一层进行抽样时,采用简单随机抽样的方法.
(4)分层抽样能充分利用已掌握的信息,使样本具有良好的代表性.
知识梳理
知识点二 分层抽样的实施步骤
1.将总体按一定标准 .
2.计算 .
3.按 的比确定各层应抽取的样本容量.
4.在每一层进行抽样(可用 ).
分层
各层的个体数与总体的个体数的比
各层的个体数占总体的个体数
简单随机抽样
知识梳理
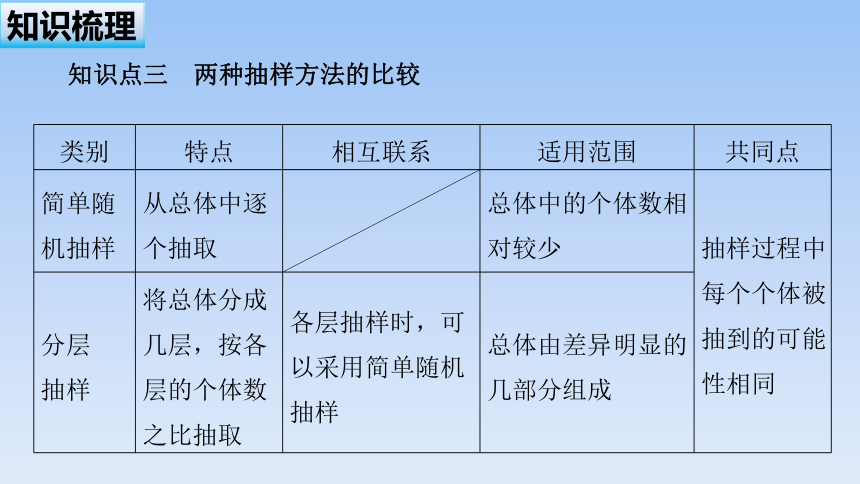
知识点三 两种抽样方法的比较
类别 特点 相互联系 适用范围 共同点
简单随机抽样 从总体中逐个抽取 总体中的个体数相对较少 抽样过程中每个个体被抽到的可能性相同
分层 抽样 将总体分成几层,按各层的个体数之比抽取 各层抽样时,可以采用简单随机抽样 总体由差异明显的几部分组成 知识梳理
2
题型探究
PART TWO
例1 ①某班数学期中考试有14人在120分以上,35人在90~119分,7人不及格,现从中抽出8人研讨进一步改进教与学;②高一某班级春节聚会,要产生两位“幸运者”.就这两件事,合适的抽样方法分别为
A.分层抽样,简单随机抽样 B.简单随机抽样,分层抽样
C.简单随机抽样,简单随机抽样 D.分层抽样,分层抽样
一、对分层抽样概念的理解
解析 ①由于学生分成了差异比较大的几部分,应用分层抽样.
②由于总体与样本容量较小,应用简单随机抽样.
√
题型探究
判断抽样方法是分层抽样,主要是依据分层抽样的特点
(1)适用于总体由差异明显的几部分组成的情况.
(2)样本能更充分地反映总体的情况.
(3)等可能抽样,每个个体被抽到的可能性都相等.
反思感悟
跟踪训练1 在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本.
方法1:采用简单随机抽样的方法,将零件编号为00,01,02,…,99,用抽签法抽取20个.
方法2:采用分层抽样的方法,从一级品中随机抽取4个,从二级品中随机抽取6个,从三级品中随机抽取10个.
对于上述问题,下列说法正确的是________.(填序号)
①不论采用哪种抽样方法,这100个零件中每一个零件被抽到的可能性都是 ;
②采用不同的方法,这100个零件中每一个零件被抽到的可能性各不相同;
③在上述两种抽样方法中,方法2抽到的样本比方法1抽到的样本更能反映总体特征.
①③
题型探究
由于总体中有差异较明显的三个层(一级品、二级品和三级品),故方法2抽到的样本更有代表性,③正确.故①③正确.
题型探究
例2 一个单位有职工500人,其中不到35岁的有125人,35岁至49岁的有280人,50岁及50岁以上的有95人.为了了解这个单位职工与身体状态有关的某项指标,要从中抽取100名职工作为样本,职工年龄与这项指标有关,应该怎样抽取?
二、分层抽样的应用
题型探究
解 用分层抽样来抽取样本,步骤如下:
(1)分层.按年龄将500名职工分成三层:不到35岁的职工;35岁至49岁的职工;50岁及50岁以上的职工.
(3)在各层分别按随机数表法抽取样本. (4)汇总每层抽样,组成样本.
题型探究
利用分层抽样抽取样本的操作步骤
(1)将总体按一定标准进行分层.
(2)计算各层的个体数与总体的个体数的比.
(3)按各层的个体数占总体的比确定各层应抽取的样本容量.
(4)在每一层进行抽样(可用简单随机抽样).
(5)最后将每一层抽取的样本汇总合成样本.
反思感悟
跟踪训练2 某市的3个区共有高中学生20 000人,且3个区的高中学生人数之比为2∶3∶5,现要从所有学生中抽取一个容量为200的样本,调查该市高中学生的视力情况,试写出抽样过程.
题型探究
解 (1)由于该市高中学生的视力有差异,按3个区分成三层,用分层抽样来抽取样本.
(3)在各层分别按简单随机抽样抽取样本.
(4)综合每层抽样,组成容量为200的样本.
题型探究
题型三 分层随机抽样中的计算问题
【例3】 (1)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层随机抽样调查,假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为( )
A.101 B.808 C.1212 D.2012
(2)将一个总体分为A,B,C三层,其个体数之比为5∶3∶2.若用分层随机抽样方法抽取容量为100的样本,则应从C中抽取________个个体.
(3)分层随机抽样中,总体共分为2层,第1层的样本量为20,样本平均数为3,第2层的样本量为30,样本平均数为8,则该样本的平均数为________.
题型探究
答案 (1)B (2)20 (3)6
题型探究
3
检测反馈
PART THREE
1.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工为7人,则样本容量为
A.12 B.13 C.14 D.15
1
2
3
4
5
√
检测反馈
2.某校对全校1 200名男女学生进行健康调查,采用分层抽样法抽取一个容量为200的样本.已知女生抽了85人,则该校的男生人数为
A.670 B.680 C.690 D.700
1
2
3
4
5
√
检测反馈
1
2
3
4
5
4
3.为了调查某省各城市PM2.5的值,按地域把36个城市分成甲、乙、丙三组,对应的城市数分别为6,12,18.若用分层抽样的方法抽取12个城市,则乙组中应抽取的城市数为_____.
检测反馈
1
2
3
4
5
4.某商场有四类食品,食品类别和种数见下表:
解析 因为总体的个数为40+10+30+20=100,所以根据分层抽样的定义可知,
6
类别 粮食类 植物油类 动物性食品类 果蔬类
种数 40 10 30 20
现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样方法抽取样本,则抽取的植物油类与果蔬类食品种数之和为________.
所以抽取的植物油类与果蔬类食品种数之和为2+4=6.
检测反馈
1
2
3
4
5
5.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的表格:
产品类别 A B C
产品数量(件) 1 300
样本数量(件) 130
由于不小心,表格中A,C产品的有关数据已被污染看不清楚,统计员记得A产品的样本数量比C产品的样本数量多10,根据以上信息,可得C产品的数量是________.
800
检测反馈
1
2
3
4
5
解析 设C产品的样本数量为n,则A产品的样本数量为n+10,
检测反馈
1.知识清单:
(1)分层抽样.
(2)分层抽样的应用.
2.方法归纳:数据分析.
3.常见误区:在分层抽样中,易忽略每个个体被抽到的可能性相等,与层数及分层无关而致错,每一层的抽样一般采用简单随机抽样.
课堂小结
苏教版必修第二册
第14章
14.2.2 分层抽样
某市为调查中小学生的近视情况,在全市范围内对小学生、初中生、高中生三个群体抽样,进而了解中小学生的总体情况和三个群体近视情况的差异大小.
问题 1.上述问题中总体有什么特征?
2.采用抽签法合适吗?若不合适,应该用什么方法抽取样本?
提示 1.该总体中,小学生、初中生、高中生三个群体在年龄、体质等方面存在着明显的差异.
2.不合适,若用抽签法,抽取的样本可能集中于某一个群体,不具有代表性.应该用分层随机抽样抽取样本.
情景引入
内
容
索
引
知识梳理
题型探究
检测反馈
1
知识梳理
PART ONE
知识点一 分层抽样
1.分层抽样的定义
一般地,当总体由差异明显的几个部分组成时,为了使样本更客观地反映总体情况,我们常常将总体中的个体按 分成层次比较分明的几个部分,然后按各个部分在总体中 实施抽样,这种抽样方法叫作分层抽样,所分成的各个部分称为“层”.
不同的特点
所占的比
知识梳理
2.分层抽样的特点
(1)适用于总体由差异明显的几部分组成的情况.
(2)按比例确定每层抽取个体的个数.
(3)在每一层进行抽样时,采用简单随机抽样的方法.
(4)分层抽样能充分利用已掌握的信息,使样本具有良好的代表性.
知识梳理
知识点二 分层抽样的实施步骤
1.将总体按一定标准 .
2.计算 .
3.按 的比确定各层应抽取的样本容量.
4.在每一层进行抽样(可用 ).
分层
各层的个体数与总体的个体数的比
各层的个体数占总体的个体数
简单随机抽样
知识梳理
知识点三 两种抽样方法的比较
类别 特点 相互联系 适用范围 共同点
简单随机抽样 从总体中逐个抽取 总体中的个体数相对较少 抽样过程中每个个体被抽到的可能性相同
分层 抽样 将总体分成几层,按各层的个体数之比抽取 各层抽样时,可以采用简单随机抽样 总体由差异明显的几部分组成 知识梳理
2
题型探究
PART TWO
例1 ①某班数学期中考试有14人在120分以上,35人在90~119分,7人不及格,现从中抽出8人研讨进一步改进教与学;②高一某班级春节聚会,要产生两位“幸运者”.就这两件事,合适的抽样方法分别为
A.分层抽样,简单随机抽样 B.简单随机抽样,分层抽样
C.简单随机抽样,简单随机抽样 D.分层抽样,分层抽样
一、对分层抽样概念的理解
解析 ①由于学生分成了差异比较大的几部分,应用分层抽样.
②由于总体与样本容量较小,应用简单随机抽样.
√
题型探究
判断抽样方法是分层抽样,主要是依据分层抽样的特点
(1)适用于总体由差异明显的几部分组成的情况.
(2)样本能更充分地反映总体的情况.
(3)等可能抽样,每个个体被抽到的可能性都相等.
反思感悟
跟踪训练1 在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本.
方法1:采用简单随机抽样的方法,将零件编号为00,01,02,…,99,用抽签法抽取20个.
方法2:采用分层抽样的方法,从一级品中随机抽取4个,从二级品中随机抽取6个,从三级品中随机抽取10个.
对于上述问题,下列说法正确的是________.(填序号)
①不论采用哪种抽样方法,这100个零件中每一个零件被抽到的可能性都是 ;
②采用不同的方法,这100个零件中每一个零件被抽到的可能性各不相同;
③在上述两种抽样方法中,方法2抽到的样本比方法1抽到的样本更能反映总体特征.
①③
题型探究
由于总体中有差异较明显的三个层(一级品、二级品和三级品),故方法2抽到的样本更有代表性,③正确.故①③正确.
题型探究
例2 一个单位有职工500人,其中不到35岁的有125人,35岁至49岁的有280人,50岁及50岁以上的有95人.为了了解这个单位职工与身体状态有关的某项指标,要从中抽取100名职工作为样本,职工年龄与这项指标有关,应该怎样抽取?
二、分层抽样的应用
题型探究
解 用分层抽样来抽取样本,步骤如下:
(1)分层.按年龄将500名职工分成三层:不到35岁的职工;35岁至49岁的职工;50岁及50岁以上的职工.
(3)在各层分别按随机数表法抽取样本. (4)汇总每层抽样,组成样本.
题型探究
利用分层抽样抽取样本的操作步骤
(1)将总体按一定标准进行分层.
(2)计算各层的个体数与总体的个体数的比.
(3)按各层的个体数占总体的比确定各层应抽取的样本容量.
(4)在每一层进行抽样(可用简单随机抽样).
(5)最后将每一层抽取的样本汇总合成样本.
反思感悟
跟踪训练2 某市的3个区共有高中学生20 000人,且3个区的高中学生人数之比为2∶3∶5,现要从所有学生中抽取一个容量为200的样本,调查该市高中学生的视力情况,试写出抽样过程.
题型探究
解 (1)由于该市高中学生的视力有差异,按3个区分成三层,用分层抽样来抽取样本.
(3)在各层分别按简单随机抽样抽取样本.
(4)综合每层抽样,组成容量为200的样本.
题型探究
题型三 分层随机抽样中的计算问题
【例3】 (1)交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层随机抽样调查,假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为( )
A.101 B.808 C.1212 D.2012
(2)将一个总体分为A,B,C三层,其个体数之比为5∶3∶2.若用分层随机抽样方法抽取容量为100的样本,则应从C中抽取________个个体.
(3)分层随机抽样中,总体共分为2层,第1层的样本量为20,样本平均数为3,第2层的样本量为30,样本平均数为8,则该样本的平均数为________.
题型探究
答案 (1)B (2)20 (3)6
题型探究
3
检测反馈
PART THREE
1.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本.若样本中的青年职工为7人,则样本容量为
A.12 B.13 C.14 D.15
1
2
3
4
5
√
检测反馈
2.某校对全校1 200名男女学生进行健康调查,采用分层抽样法抽取一个容量为200的样本.已知女生抽了85人,则该校的男生人数为
A.670 B.680 C.690 D.700
1
2
3
4
5
√
检测反馈
1
2
3
4
5
4
3.为了调查某省各城市PM2.5的值,按地域把36个城市分成甲、乙、丙三组,对应的城市数分别为6,12,18.若用分层抽样的方法抽取12个城市,则乙组中应抽取的城市数为_____.
检测反馈
1
2
3
4
5
4.某商场有四类食品,食品类别和种数见下表:
解析 因为总体的个数为40+10+30+20=100,所以根据分层抽样的定义可知,
6
类别 粮食类 植物油类 动物性食品类 果蔬类
种数 40 10 30 20
现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样方法抽取样本,则抽取的植物油类与果蔬类食品种数之和为________.
所以抽取的植物油类与果蔬类食品种数之和为2+4=6.
检测反馈
1
2
3
4
5
5.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的表格:
产品类别 A B C
产品数量(件) 1 300
样本数量(件) 130
由于不小心,表格中A,C产品的有关数据已被污染看不清楚,统计员记得A产品的样本数量比C产品的样本数量多10,根据以上信息,可得C产品的数量是________.
800
检测反馈
1
2
3
4
5
解析 设C产品的样本数量为n,则A产品的样本数量为n+10,
检测反馈
1.知识清单:
(1)分层抽样.
(2)分层抽样的应用.
2.方法归纳:数据分析.
3.常见误区:在分层抽样中,易忽略每个个体被抽到的可能性相等,与层数及分层无关而致错,每一层的抽样一般采用简单随机抽样.
课堂小结
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
