苏教版(2019)高中数学必修第二册 14.2.2分层抽样练习(解析版)
文档属性
| 名称 | 苏教版(2019)高中数学必修第二册 14.2.2分层抽样练习(解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 10:00:22 | ||
图片预览



文档简介
14.2.2 分层抽样
1.下列实验中最适合用分层抽样法抽样的是( )
A.从一箱3 000个零件中抽取5个入样
B.从一箱3 000个零件中抽取600个入样
C.从一箱30个零件中抽取5个入样
D.从甲厂生产的100个零件和乙厂生产的200个零件中抽取6个入样
2.将A,B,C三种性质的个体按1∶2∶4的比例进行分层抽样调查,若抽取的样本容量为21,则A,B,C三种性质的个体分别抽取的个数为( )
A.12,6,3 B.12,3,6
C.3,6,12 D.3,12,6
3.某中学有高中生3 500人,初中生1 500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150
C.200 D.250
4.我国古代数学名著《九章算术》中有如下问题“今有北乡算八千七百五十八,西乡算七千二百三十六,南乡算八千三百五十六,凡三乡,发役三百七十八人,欲以算数多少出之,问各几何?”意思是:北乡有8 758人,西乡有7 236人,南乡有8 356人,现要按人数多少从三乡共征集378人,问从各乡征集多少人?在上述问题中,需从西乡征集的人数是( )
A.102 B.112
C.130 D.136
5.某学校高一、高二、高三三个年级共有学生3 500人,其中高三学生人数是高一学生人数的两倍,高二学生人数比高一学生人数多300,现在按的抽样比用分层抽样的方法抽取样本,则应抽取的高一学生人数为( )
A.8 B.11 C.16 D.10
6.已知高一年级有学生450人,高二年级有学生750人,高三年级有学生600人,用分层抽样从该校的这三个年级中抽取一个样本,且每个学生被抽到的可能性为0.02,则应从高二年级抽取的学生人数为________.
7.某学校高一年级有x个学生,高二年级有y个学生,高三年级有z个学生.现采用分层抽样法抽取一个容量为45的样本,其中高一年级被抽取20人,高三年级被抽取10人,高二年级共有300人,则此学校共有高中学生______人.
8.某橘子园有平地和山地共120亩,现在要估计平均亩产量,按一定的比例用分层抽样的方法共抽取10亩进行统计.如果所抽取的山地是平地的2倍多1亩,则这个橘子园的平地与山地的亩数分别为________.
9.为了对某课题进行研究,分别从A,B,C三所高校中用分层抽样法抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中0<m≤72≤n).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授总数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
10.某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3 000名初中生、4 000名高中生中做问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3 000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
11.某校共有学生2 000名,各年级男、女生人数如下表所示:
一年级 二年级 三年级
女生 373 380 y
男生 377 370 z
现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
A.24 B.18
C.16 D.12
12.某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80
C.120 D.180
13.某机构对某镇的学生的身体素质状况按年级段进行分层抽样调查,得到了如下表所示的数据,则=______.
年级段 小学 初中 高中
总人数 800 x y
样本中人数 16 15 z
14.某高中针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级 高二年级 高三年级
泥塑 a b c
剪纸 x y z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取________人.
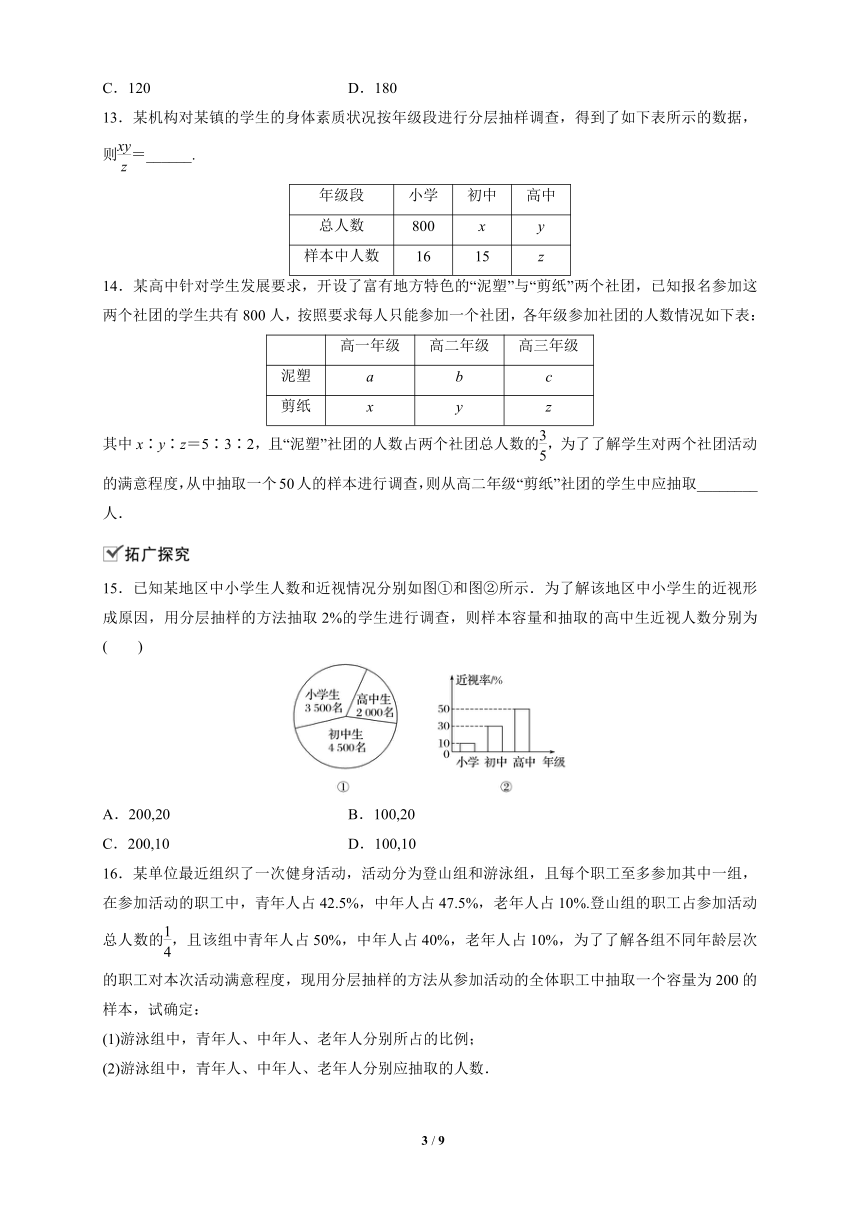
15.已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
A.200,20 B.100,20
C.200,10 D.100,10
16.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%,为了了解各组不同年龄层次的职工对本次活动满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
14.2.2 分层抽样解析答案
1.下列实验中最适合用分层抽样法抽样的是( )
A.从一箱3 000个零件中抽取5个入样
B.从一箱3 000个零件中抽取600个入样
C.从一箱30个零件中抽取5个入样
D.从甲厂生产的100个零件和乙厂生产的200个零件中抽取6个入样
【答案】 D
【解析】 D中总体有明显差异,故用分层抽样.
2.将A,B,C三种性质的个体按1∶2∶4的比例进行分层抽样调查,若抽取的样本容量为21,则A,B,C三种性质的个体分别抽取的个数为( )
A.12,6,3 B.12,3,6
C.3,6,12 D.3,12,6
【答案】 C
【解析】 由分层抽样的概念,知A,B,C三种性质的个体应分别抽取的个数为21×=3,21×=6,21×=12.
3.某中学有高中生3 500人,初中生1 500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150
C.200 D.250
【答案】 A
【解析】 由题意得,=,解得n=100.
4.我国古代数学名著《九章算术》中有如下问题“今有北乡算八千七百五十八,西乡算七千二百三十六,南乡算八千三百五十六,凡三乡,发役三百七十八人,欲以算数多少出之,问各几何?”意思是:北乡有8 758人,西乡有7 236人,南乡有8 356人,现要按人数多少从三乡共征集378人,问从各乡征集多少人?在上述问题中,需从西乡征集的人数是( )
A.102 B.112
C.130 D.136
【答案】 B
【解析】 因为北乡有8 758人,西乡有7 236人,南乡有8 356人,现要按人数多少从三乡共征集378人,故需从西乡征集的人数是378×≈112.
5.某学校高一、高二、高三三个年级共有学生3 500人,其中高三学生人数是高一学生人数的两倍,高二学生人数比高一学生人数多300,现在按的抽样比用分层抽样的方法抽取样本,则应抽取的高一学生人数为( )
A.8 B.11 C.16 D.10
【答案】 A
【解析】 若设高三学生人数为x,则高一学生人数为,高二学生人数为+300,所以有x+++300=3 500,解得x=1 600.故高一学生人数为800,因此应抽取的高一学生人数为=8.
6.已知高一年级有学生450人,高二年级有学生750人,高三年级有学生600人,用分层抽样从该校的这三个年级中抽取一个样本,且每个学生被抽到的可能性为0.02,则应从高二年级抽取的学生人数为________.
【答案】 15
【解析】 因为每个学生被抽到的可能性为0.02,所以从高二年级抽取的学生人数为0.02×750=15.
7.某学校高一年级有x个学生,高二年级有y个学生,高三年级有z个学生.现采用分层抽样法抽取一个容量为45的样本,其中高一年级被抽取20人,高三年级被抽取10人,高二年级共有300人,则此学校共有高中学生______人.
【答案】 900
【解析】 高二年级被抽取45-20-10=15(人),
被抽取的比例为=,所以x=400,z=200.
所以此学校共有高中学生900人.
8.某橘子园有平地和山地共120亩,现在要估计平均亩产量,按一定的比例用分层抽样的方法共抽取10亩进行统计.如果所抽取的山地是平地的2倍多1亩,则这个橘子园的平地与山地的亩数分别为________.
【答案】 36,84
【解析】 设所抽取的平地的亩数为x,则抽取的山地的亩数为2x+1,∴x+2x+1=10,得x=3,∴这个橘子园的平地的亩数为120×=36,山地的亩数为120-36=84.
9.为了对某课题进行研究,分别从A,B,C三所高校中用分层抽样法抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中0<m≤72≤n).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授总数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
解 (1)∵0<m≤72≤n,A,B两所高校中共抽取3名教授,∴高校B中抽取2人,
∴高校A中抽取1人,高校C中抽取3人,
∴==,解得m=36,n=108.
(2)∵高校B中抽取的教授总数是高校A和C中抽取的教授总数的,
∴(m+n)=72,解得m+n=108,
∴三所高校的教授的总人数为m+n+72=180.
10.某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3 000名初中生、4 000名高中生中做问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3 000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
解 (1)由于这次活动对教职员工、初中生和高中生产生的影响不会相同,所以应当采取分层抽样的方法进行抽样.
因为样本容量为120,总体个数为500+3 000+4 000=7 500,则抽样比为=,
所以500×=8,3 000×=48,4 000×=64,所以在教职员工、初中生、高中生中抽取的个体数分别是8,48,64.
分层抽样的步骤是
①分层:将全校师生分为教职员工、初中生、高中生,共三层.
②确定每层抽取个体的个数:在教职员工、初中生、高中生中抽取的个体数分别是8,48,64.
③各层分别按简单随机抽样的方法抽取样本.
④综合每层抽样,组成样本.
这样便完成了整个抽样过程,就能得到比较客观的评价结论.
(2)由于简单随机抽样有两种方法:抽签法和随机数表法.如果用抽签法,要作3 000个号签,费时费力,因此采用随机数表法抽取样本,步骤是
①编号:将3 000份答卷都编上号码:0001,0002,0003,…,3000.
②在随机数表上随机选取一个起始位置.
③规定读数方向:向右连续取数字,以4个数为一组,如果读取的4位数大于3000,则去掉,如果遇到相同号码则只取一个,这样一直到取满48个号码为止.
11.某校共有学生2 000名,各年级男、女生人数如下表所示:
一年级 二年级 三年级
女生 373 380 y
男生 377 370 z
现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
A.24 B.18
C.16 D.12
【答案】 C
【解析】 一年级的学生人数为373+377=750,二年级的学生人数为380+370=750,于是三年级的学生人数为2 000-750-750=500,那么三年级应抽取的人数为500×=16.
12.某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80
C.120 D.180
【答案】 C
【解析】 11~12岁回收180份,其中在11~12岁学生问卷中抽取60份,抽样比为,因为分层抽取的样本容量为300,故回收问卷总数为=900(份),故x=900-120-180-240=360(份),360×=120(份).
13.某机构对某镇的学生的身体素质状况按年级段进行分层抽样调查,得到了如下表所示的数据,则=______.
年级段 小学 初中 高中
总人数 800 x y
样本中人数 16 15 z
【答案】 37 500
【解析】 由分层抽样的特点,得==,即x=750,=50,则=37 500.
14.某高中针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级 高二年级 高三年级
泥塑 a b c
剪纸 x y z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取________人.
【答案】 6
【解析】 因为“泥塑”社团的人数占总人数的,故“剪纸”社团的人数占总人数的,所以“剪纸”社团的人数为800×=320.因为“剪纸”社团中高二年级人数比例为==,所以“剪纸”社团中高二年级人数为320×=96.由题意知,抽样比为=,所以从高二年级“剪纸”社团中抽取的人数为96×=6.
15.已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
A.200,20 B.100,20
C.200,10 D.100,10
【答案】 A
【解析】 该地区中小学生总人数为3 500+2 000+4 500=10 000,
则样本容量为10 000×2%=200,其中抽取的高中生近视人数为2 000×2%×50%=20.
16.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%,为了了解各组不同年龄层次的职工对本次活动满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
解 (1)设登山组人数为x,游泳组中,青年人、中年人、老年人所占比例分别为a,b,c,
则有=47.5%,=10%,
解得b=50%,c=10%,
故a=100%-50%-10%=40%.
即游泳组中,青年人、中年人、老年人所占比例分别为40%,50%,10%.
(2)游泳组中,
抽取的青年人人数为200××40%=60;
抽取的中年人人数为200××50%=75;
抽取的老年人人数为200××10%=15.
即游泳组中,青年人、中年人、老年人分别应抽取的人数为60,75,15.
2 / 9
1.下列实验中最适合用分层抽样法抽样的是( )
A.从一箱3 000个零件中抽取5个入样
B.从一箱3 000个零件中抽取600个入样
C.从一箱30个零件中抽取5个入样
D.从甲厂生产的100个零件和乙厂生产的200个零件中抽取6个入样
2.将A,B,C三种性质的个体按1∶2∶4的比例进行分层抽样调查,若抽取的样本容量为21,则A,B,C三种性质的个体分别抽取的个数为( )
A.12,6,3 B.12,3,6
C.3,6,12 D.3,12,6
3.某中学有高中生3 500人,初中生1 500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150
C.200 D.250
4.我国古代数学名著《九章算术》中有如下问题“今有北乡算八千七百五十八,西乡算七千二百三十六,南乡算八千三百五十六,凡三乡,发役三百七十八人,欲以算数多少出之,问各几何?”意思是:北乡有8 758人,西乡有7 236人,南乡有8 356人,现要按人数多少从三乡共征集378人,问从各乡征集多少人?在上述问题中,需从西乡征集的人数是( )
A.102 B.112
C.130 D.136
5.某学校高一、高二、高三三个年级共有学生3 500人,其中高三学生人数是高一学生人数的两倍,高二学生人数比高一学生人数多300,现在按的抽样比用分层抽样的方法抽取样本,则应抽取的高一学生人数为( )
A.8 B.11 C.16 D.10
6.已知高一年级有学生450人,高二年级有学生750人,高三年级有学生600人,用分层抽样从该校的这三个年级中抽取一个样本,且每个学生被抽到的可能性为0.02,则应从高二年级抽取的学生人数为________.
7.某学校高一年级有x个学生,高二年级有y个学生,高三年级有z个学生.现采用分层抽样法抽取一个容量为45的样本,其中高一年级被抽取20人,高三年级被抽取10人,高二年级共有300人,则此学校共有高中学生______人.
8.某橘子园有平地和山地共120亩,现在要估计平均亩产量,按一定的比例用分层抽样的方法共抽取10亩进行统计.如果所抽取的山地是平地的2倍多1亩,则这个橘子园的平地与山地的亩数分别为________.
9.为了对某课题进行研究,分别从A,B,C三所高校中用分层抽样法抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中0<m≤72≤n).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授总数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
10.某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3 000名初中生、4 000名高中生中做问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3 000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
11.某校共有学生2 000名,各年级男、女生人数如下表所示:
一年级 二年级 三年级
女生 373 380 y
男生 377 370 z
现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
A.24 B.18
C.16 D.12
12.某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80
C.120 D.180
13.某机构对某镇的学生的身体素质状况按年级段进行分层抽样调查,得到了如下表所示的数据,则=______.
年级段 小学 初中 高中
总人数 800 x y
样本中人数 16 15 z
14.某高中针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级 高二年级 高三年级
泥塑 a b c
剪纸 x y z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取________人.
15.已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
A.200,20 B.100,20
C.200,10 D.100,10
16.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%,为了了解各组不同年龄层次的职工对本次活动满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
14.2.2 分层抽样解析答案
1.下列实验中最适合用分层抽样法抽样的是( )
A.从一箱3 000个零件中抽取5个入样
B.从一箱3 000个零件中抽取600个入样
C.从一箱30个零件中抽取5个入样
D.从甲厂生产的100个零件和乙厂生产的200个零件中抽取6个入样
【答案】 D
【解析】 D中总体有明显差异,故用分层抽样.
2.将A,B,C三种性质的个体按1∶2∶4的比例进行分层抽样调查,若抽取的样本容量为21,则A,B,C三种性质的个体分别抽取的个数为( )
A.12,6,3 B.12,3,6
C.3,6,12 D.3,12,6
【答案】 C
【解析】 由分层抽样的概念,知A,B,C三种性质的个体应分别抽取的个数为21×=3,21×=6,21×=12.
3.某中学有高中生3 500人,初中生1 500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150
C.200 D.250
【答案】 A
【解析】 由题意得,=,解得n=100.
4.我国古代数学名著《九章算术》中有如下问题“今有北乡算八千七百五十八,西乡算七千二百三十六,南乡算八千三百五十六,凡三乡,发役三百七十八人,欲以算数多少出之,问各几何?”意思是:北乡有8 758人,西乡有7 236人,南乡有8 356人,现要按人数多少从三乡共征集378人,问从各乡征集多少人?在上述问题中,需从西乡征集的人数是( )
A.102 B.112
C.130 D.136
【答案】 B
【解析】 因为北乡有8 758人,西乡有7 236人,南乡有8 356人,现要按人数多少从三乡共征集378人,故需从西乡征集的人数是378×≈112.
5.某学校高一、高二、高三三个年级共有学生3 500人,其中高三学生人数是高一学生人数的两倍,高二学生人数比高一学生人数多300,现在按的抽样比用分层抽样的方法抽取样本,则应抽取的高一学生人数为( )
A.8 B.11 C.16 D.10
【答案】 A
【解析】 若设高三学生人数为x,则高一学生人数为,高二学生人数为+300,所以有x+++300=3 500,解得x=1 600.故高一学生人数为800,因此应抽取的高一学生人数为=8.
6.已知高一年级有学生450人,高二年级有学生750人,高三年级有学生600人,用分层抽样从该校的这三个年级中抽取一个样本,且每个学生被抽到的可能性为0.02,则应从高二年级抽取的学生人数为________.
【答案】 15
【解析】 因为每个学生被抽到的可能性为0.02,所以从高二年级抽取的学生人数为0.02×750=15.
7.某学校高一年级有x个学生,高二年级有y个学生,高三年级有z个学生.现采用分层抽样法抽取一个容量为45的样本,其中高一年级被抽取20人,高三年级被抽取10人,高二年级共有300人,则此学校共有高中学生______人.
【答案】 900
【解析】 高二年级被抽取45-20-10=15(人),
被抽取的比例为=,所以x=400,z=200.
所以此学校共有高中学生900人.
8.某橘子园有平地和山地共120亩,现在要估计平均亩产量,按一定的比例用分层抽样的方法共抽取10亩进行统计.如果所抽取的山地是平地的2倍多1亩,则这个橘子园的平地与山地的亩数分别为________.
【答案】 36,84
【解析】 设所抽取的平地的亩数为x,则抽取的山地的亩数为2x+1,∴x+2x+1=10,得x=3,∴这个橘子园的平地的亩数为120×=36,山地的亩数为120-36=84.
9.为了对某课题进行研究,分别从A,B,C三所高校中用分层抽样法抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中0<m≤72≤n).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授总数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
解 (1)∵0<m≤72≤n,A,B两所高校中共抽取3名教授,∴高校B中抽取2人,
∴高校A中抽取1人,高校C中抽取3人,
∴==,解得m=36,n=108.
(2)∵高校B中抽取的教授总数是高校A和C中抽取的教授总数的,
∴(m+n)=72,解得m+n=108,
∴三所高校的教授的总人数为m+n+72=180.
10.某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3 000名初中生、4 000名高中生中做问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3 000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
解 (1)由于这次活动对教职员工、初中生和高中生产生的影响不会相同,所以应当采取分层抽样的方法进行抽样.
因为样本容量为120,总体个数为500+3 000+4 000=7 500,则抽样比为=,
所以500×=8,3 000×=48,4 000×=64,所以在教职员工、初中生、高中生中抽取的个体数分别是8,48,64.
分层抽样的步骤是
①分层:将全校师生分为教职员工、初中生、高中生,共三层.
②确定每层抽取个体的个数:在教职员工、初中生、高中生中抽取的个体数分别是8,48,64.
③各层分别按简单随机抽样的方法抽取样本.
④综合每层抽样,组成样本.
这样便完成了整个抽样过程,就能得到比较客观的评价结论.
(2)由于简单随机抽样有两种方法:抽签法和随机数表法.如果用抽签法,要作3 000个号签,费时费力,因此采用随机数表法抽取样本,步骤是
①编号:将3 000份答卷都编上号码:0001,0002,0003,…,3000.
②在随机数表上随机选取一个起始位置.
③规定读数方向:向右连续取数字,以4个数为一组,如果读取的4位数大于3000,则去掉,如果遇到相同号码则只取一个,这样一直到取满48个号码为止.
11.某校共有学生2 000名,各年级男、女生人数如下表所示:
一年级 二年级 三年级
女生 373 380 y
男生 377 370 z
现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
A.24 B.18
C.16 D.12
【答案】 C
【解析】 一年级的学生人数为373+377=750,二年级的学生人数为380+370=750,于是三年级的学生人数为2 000-750-750=500,那么三年级应抽取的人数为500×=16.
12.某校做了一次关于“感恩父母”的问卷调查,从8~10岁,11~12岁,13~14岁,15~16岁四个年龄段回收的问卷依次为:120份,180份,240份,x份.因调查需要,从回收的问卷中按年龄段分层抽取容量为300的样本,其中在11~12岁学生问卷中抽取60份,则在15~16岁学生中抽取的问卷份数为( )
A.60 B.80
C.120 D.180
【答案】 C
【解析】 11~12岁回收180份,其中在11~12岁学生问卷中抽取60份,抽样比为,因为分层抽取的样本容量为300,故回收问卷总数为=900(份),故x=900-120-180-240=360(份),360×=120(份).
13.某机构对某镇的学生的身体素质状况按年级段进行分层抽样调查,得到了如下表所示的数据,则=______.
年级段 小学 初中 高中
总人数 800 x y
样本中人数 16 15 z
【答案】 37 500
【解析】 由分层抽样的特点,得==,即x=750,=50,则=37 500.
14.某高中针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级 高二年级 高三年级
泥塑 a b c
剪纸 x y z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取________人.
【答案】 6
【解析】 因为“泥塑”社团的人数占总人数的,故“剪纸”社团的人数占总人数的,所以“剪纸”社团的人数为800×=320.因为“剪纸”社团中高二年级人数比例为==,所以“剪纸”社团中高二年级人数为320×=96.由题意知,抽样比为=,所以从高二年级“剪纸”社团中抽取的人数为96×=6.
15.已知某地区中小学生人数和近视情况分别如图①和图②所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取2%的学生进行调查,则样本容量和抽取的高中生近视人数分别为( )
A.200,20 B.100,20
C.200,10 D.100,10
【答案】 A
【解析】 该地区中小学生总人数为3 500+2 000+4 500=10 000,
则样本容量为10 000×2%=200,其中抽取的高中生近视人数为2 000×2%×50%=20.
16.某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加其中一组,在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的,且该组中青年人占50%,中年人占40%,老年人占10%,为了了解各组不同年龄层次的职工对本次活动满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本,试确定:
(1)游泳组中,青年人、中年人、老年人分别所占的比例;
(2)游泳组中,青年人、中年人、老年人分别应抽取的人数.
解 (1)设登山组人数为x,游泳组中,青年人、中年人、老年人所占比例分别为a,b,c,
则有=47.5%,=10%,
解得b=50%,c=10%,
故a=100%-50%-10%=40%.
即游泳组中,青年人、中年人、老年人所占比例分别为40%,50%,10%.
(2)游泳组中,
抽取的青年人人数为200××40%=60;
抽取的中年人人数为200××50%=75;
抽取的老年人人数为200××10%=15.
即游泳组中,青年人、中年人、老年人分别应抽取的人数为60,75,15.
2 / 9
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
