平行线的性质应用[下学期]
文档属性
| 名称 | 平行线的性质应用[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 148.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-04-05 10:22:00 | ||
图片预览


文档简介
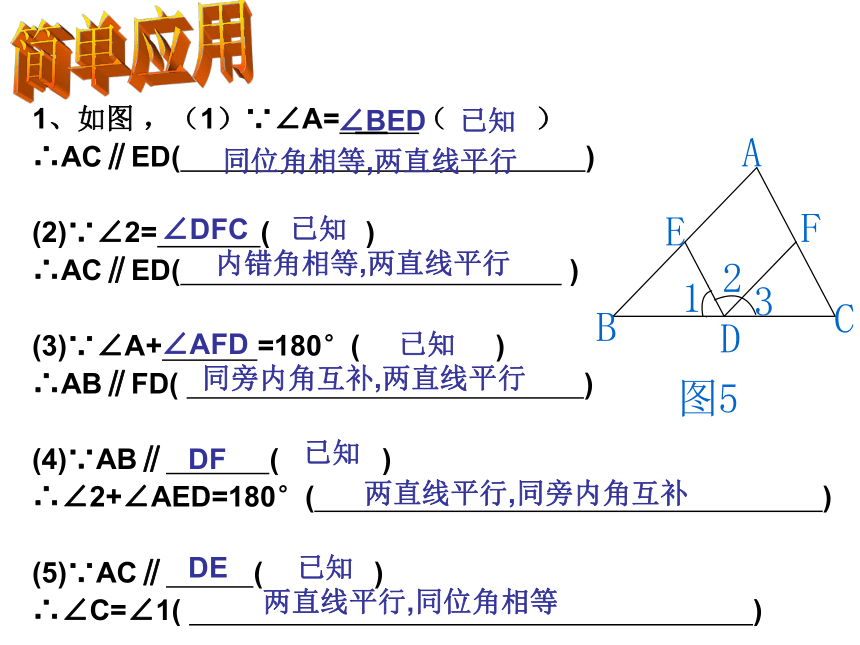
课件12张PPT。性质1:两直线平行,同位角相等.
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:复习回顾一下!∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)∵a∥b(已知)
∴∠3=∠2(两直线平行,内错角相等)∵a∥b(已知)
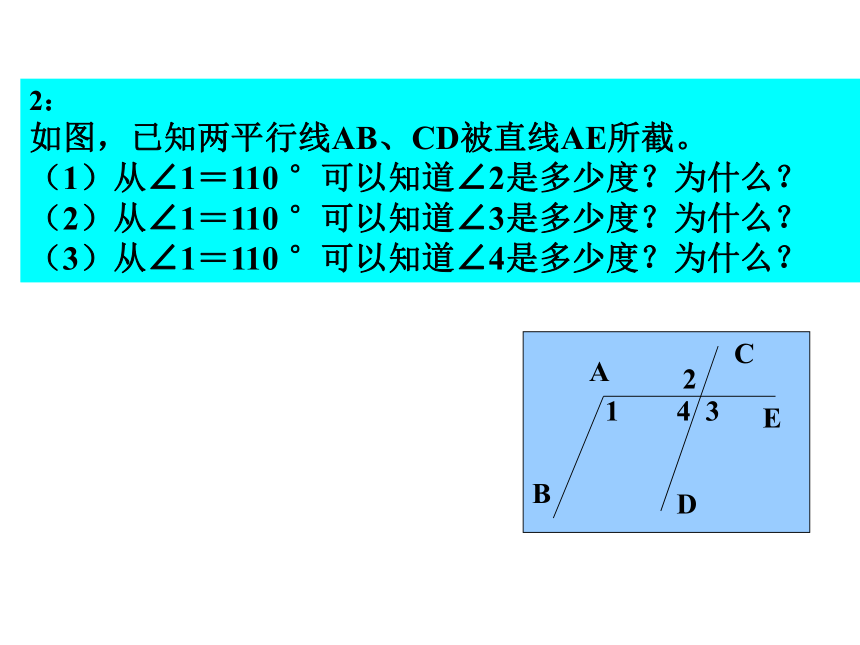
∴∠4+∠2=180°(两直线平行,同旁内角互补)1、如图 ,(1)∵∠A= __ ( )
∴AC∥ED( )
(2)∵∠2= ( )
∴AC∥ED( )
(3)∵∠A+ =180°( )
∴AB∥FD( )
(4)∵AB∥ ( )
∴∠2+∠AED=180°( )
(5)∵AC∥ ( )
∴∠C=∠1( ) 简单应用∠BED已知同位角相等,两直线平行∠DFC已知内错角相等,两直线平行∠AFD已知同旁内角互补,两直线平行DF已知两直线平行,同旁内角互补DE已知两直线平行,同位角相等2:
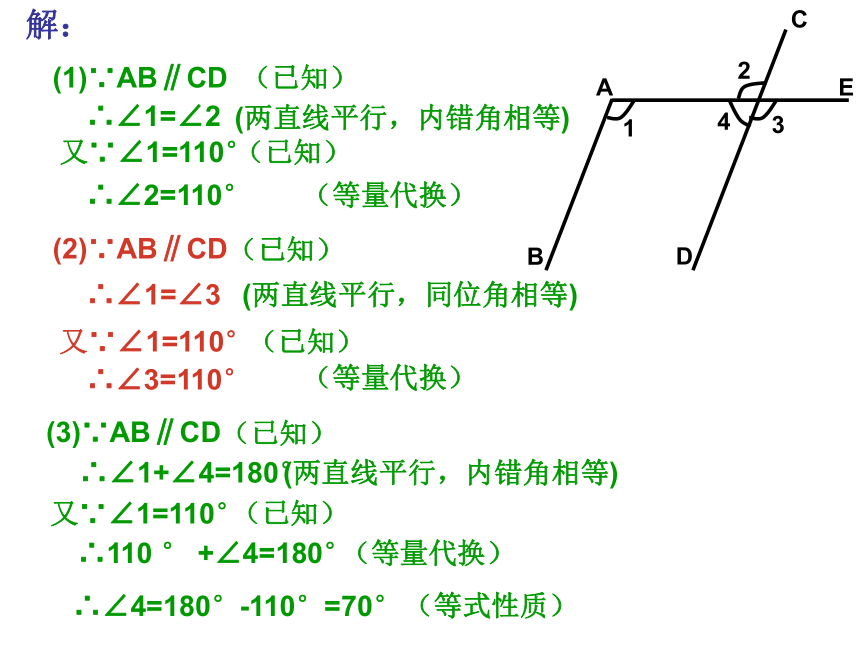
如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
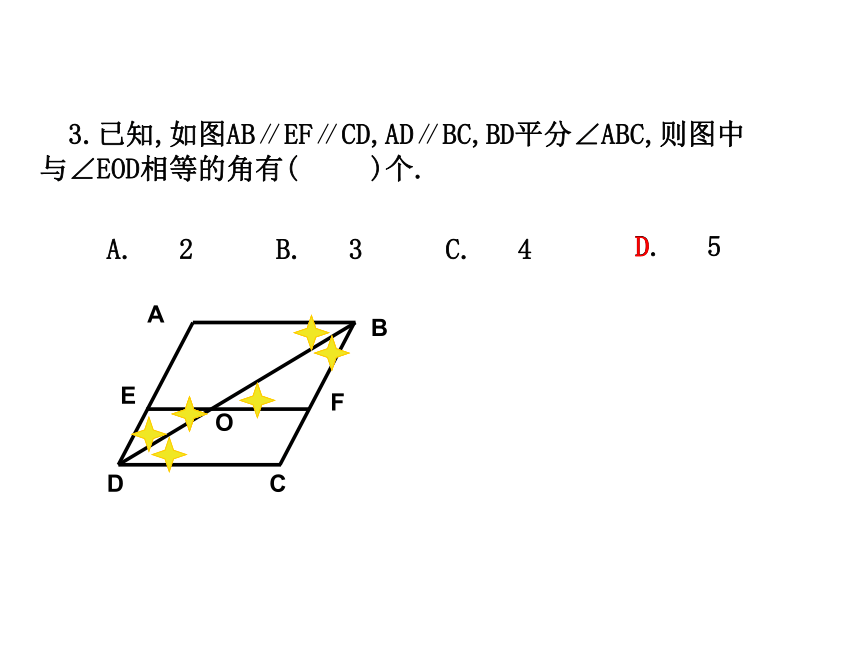
(3)从∠1=110 °可以知道∠4是多少度?为什么?(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解: 3.已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D探究可以发现,线段B1C1 ,B2C2…… B5C5同时垂直于两条平行的直线A1B5和A2C5,并且它们的长度相等。像这样,同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离。思考如图,AB∥CD,在CD上
任取一点E,向AB作垂线段
EF,这时,EF是否也垂直于
直线CD呢?我们这样作出的
垂线段EF的长度d是平行线
AB、CD的距离吗?1、如图,若AB∥DF,∠2= ∠ A,试确定DE与AC的位置关系,并说明理由.ABCDEF2例题选讲2、如图,若AD∥BC,AC平分 ∠ BAD,
∠ B=54°,求∠ C的度数.3、如图,若AB∥DC,DA平分 ∠ BDC,
DE⊥AD,∠ B=108°,求∠ A和∠BDE
的度数.45c过A画直线c∥a,A∵a∥b,∴ b∥c( )∴ ∠1+∠4=180°,∠2+∠5=180 °
( )∴ 135 ° +∠4=180°, ( )
得 ∠4=45° 120° +∠5=180°,( )
得 ∠5=60°∴ ∠3=180°-∠4-∠5
=180 °-45°-60°
=75°( 平角的定义 )再见!
性质2:两直线平行,内错角相等.
性质3:两直线平行,同旁内角互补.
平行线的性质:复习回顾一下!∵a∥b(已知)
∴∠1=∠2(两直线平行,同位角相等)∵a∥b(已知)
∴∠3=∠2(两直线平行,内错角相等)∵a∥b(已知)
∴∠4+∠2=180°(两直线平行,同旁内角互补)1、如图 ,(1)∵∠A= __ ( )
∴AC∥ED( )
(2)∵∠2= ( )
∴AC∥ED( )
(3)∵∠A+ =180°( )
∴AB∥FD( )
(4)∵AB∥ ( )
∴∠2+∠AED=180°( )
(5)∵AC∥ ( )
∴∠C=∠1( ) 简单应用∠BED已知同位角相等,两直线平行∠DFC已知内错角相等,两直线平行∠AFD已知同旁内角互补,两直线平行DF已知两直线平行,同旁内角互补DE已知两直线平行,同位角相等2:
如图,已知两平行线AB、CD被直线AE所截。
(1)从∠1=110 °可以知道∠2是多少度?为什么?
(2)从∠1=110 °可以知道∠3是多少度?为什么?
(3)从∠1=110 °可以知道∠4是多少度?为什么?(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解: 3.已知,如图AB∥EF∥CD,AD∥BC,BD平分∠ABC,则图中
与∠EOD相等的角有( )个.A. 2B. 3C. 4D. 5D探究可以发现,线段B1C1 ,B2C2…… B5C5同时垂直于两条平行的直线A1B5和A2C5,并且它们的长度相等。像这样,同时垂直于两条平行线,并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离。思考如图,AB∥CD,在CD上
任取一点E,向AB作垂线段
EF,这时,EF是否也垂直于
直线CD呢?我们这样作出的
垂线段EF的长度d是平行线
AB、CD的距离吗?1、如图,若AB∥DF,∠2= ∠ A,试确定DE与AC的位置关系,并说明理由.ABCDEF2例题选讲2、如图,若AD∥BC,AC平分 ∠ BAD,
∠ B=54°,求∠ C的度数.3、如图,若AB∥DC,DA平分 ∠ BDC,
DE⊥AD,∠ B=108°,求∠ A和∠BDE
的度数.45c过A画直线c∥a,A∵a∥b,∴ b∥c( )∴ ∠1+∠4=180°,∠2+∠5=180 °
( )∴ 135 ° +∠4=180°, ( )
得 ∠4=45° 120° +∠5=180°,( )
得 ∠5=60°∴ ∠3=180°-∠4-∠5
=180 °-45°-60°
=75°( 平角的定义 )再见!
