11.2 与三角形有关的角(第2课时)课件
文档属性
| 名称 | 11.2 与三角形有关的角(第2课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 432.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-01-14 00:00:00 | ||
图片预览



文档简介
课件18张PPT。八年级 上册11.2 与三角形有关的角
(第2课时)课件说明 在学习了三角形的内角和的基础上,本节课进一步
研究直角三角形的性质与判定,以及运用性质与判
定解决问题.学习目标:
1.探索并掌握直角三角形的两个锐角互余.
2.掌握有两个角互余的三角形是直角三角形.
学习重点:
探索并掌握直角三角形的两个锐角互余.
课件说明复习三角形的内角和 问题1 在△ABC 中,∠A =60°,∠B =30°,∠C
等于多少度?你用了什么知识解决的?探索直角三角形的性质 问题2 在△ABC 中,若∠C =90°,你能求出∠A,
∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?
利用上面的结果,你能得出什么结论? 直角三角形的两个锐
角互余. 探索直角三角形的性质 直角三角形可以用符号“Rt△”表示,
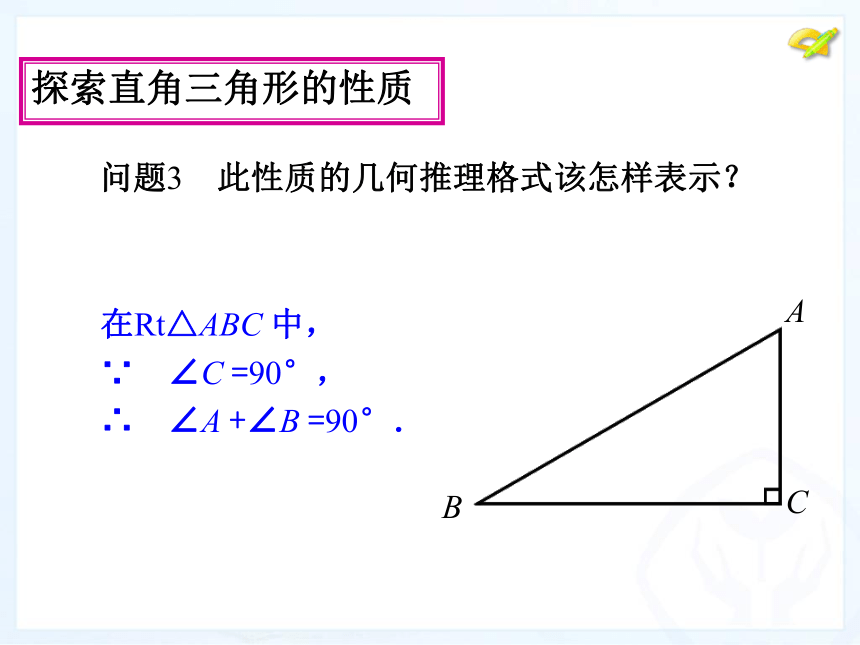
直角三角形ABC 可以写成Rt△ABC .探索直角三角形的性质在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°. 问题3 此性质的几何推理格式该怎样表示?例题讲解 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么? 分析:两个角的关系是
什么?这两个角分别在什么
三角形中?你如何验证自己
的想法?例题讲解解:在Rt△AEC 中,
∵ ∠C =90°,
∴ ∠CAE +∠AEC =90°
(直角三角形两锐角互余).
在Rt△BDE 中,
∵ ∠D =90°, 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?例题讲解解:∴ ∠DBE +∠BED =90°
(直角三角形两锐角互余).
∵ ∠AEC =∠BED
(对顶角相等),
∴ ∠CAE =∠DBE
(等角的余角相等). 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?探索直角三角形的判定 问题4 我们知道,如果一个三角形是直角三角形,
那么这个三角形有两个角互余.反过来,你能得出什么
结论?这个结论成立吗?如何验证你的想法? 利用三角形内角和定理可得:
有两个角互余的三角形是直角三角形. 探索直角三角形的判定 问题5 类比性质的几何推理格式,判定的几何推
理格式又该怎样表示? 推理格式:
在Rt△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.相等.
同角的余角相等. 课堂练习 练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?课堂练习 变式1 若∠ACD =∠B,∠ACB =90°,则CD 是
△ACB 的高吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式2 若∠ACD =∠B,CD ⊥AB,△ACB 为直角
三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式3 如图,若∠C =90°,∠AED =∠B,△ADE
是直角三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.
(证明过程略).课堂小结(1)本节课学习了哪些主要内容?
(2)你是如何探索直角三角形的性质与判定的?它们
是怎么叙述的?它们有什么区别与联系?
(3)利用直角三角形的性质与判定分别可以解决哪些
问题?布置作业教科书习题11.2第4、10题.
研究直角三角形的性质与判定,以及运用性质与判
定解决问题.学习目标:
1.探索并掌握直角三角形的两个锐角互余.
2.掌握有两个角互余的三角形是直角三角形.
学习重点:
探索并掌握直角三角形的两个锐角互余.
课件说明复习三角形的内角和 问题1 在△ABC 中,∠A =60°,∠B =30°,∠C
等于多少度?你用了什么知识解决的?探索直角三角形的性质 问题2 在△ABC 中,若∠C =90°,你能求出∠A,
∠B 的度数吗?为什么?你能求出∠A +∠B 的度数吗?
利用上面的结果,你能得出什么结论? 直角三角形的两个锐
角互余. 探索直角三角形的性质 直角三角形可以用符号“Rt△”表示,
直角三角形ABC 可以写成Rt△ABC .探索直角三角形的性质在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°. 问题3 此性质的几何推理格式该怎样表示?例题讲解 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么? 分析:两个角的关系是
什么?这两个角分别在什么
三角形中?你如何验证自己
的想法?例题讲解解:在Rt△AEC 中,
∵ ∠C =90°,
∴ ∠CAE +∠AEC =90°
(直角三角形两锐角互余).
在Rt△BDE 中,
∵ ∠D =90°, 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?例题讲解解:∴ ∠DBE +∠BED =90°
(直角三角形两锐角互余).
∵ ∠AEC =∠BED
(对顶角相等),
∴ ∠CAE =∠DBE
(等角的余角相等). 例 如图,∠C =∠D =90°,AD,BC 相交于点E,
∠CAE 与∠DBE 有什么关系?为什么?探索直角三角形的判定 问题4 我们知道,如果一个三角形是直角三角形,
那么这个三角形有两个角互余.反过来,你能得出什么
结论?这个结论成立吗?如何验证你的想法? 利用三角形内角和定理可得:
有两个角互余的三角形是直角三角形. 探索直角三角形的判定 问题5 类比性质的几何推理格式,判定的几何推
理格式又该怎样表示? 推理格式:
在Rt△ABC 中,
∵ ∠A +∠B =90°,
∴ △ABC 是直角三角形.相等.
同角的余角相等. 课堂练习 练习 如图,∠ACB =90°,CD⊥AB,垂足为D,
∠ACD 与∠B 有什么关系?为什么?课堂练习 变式1 若∠ACD =∠B,∠ACB =90°,则CD 是
△ACB 的高吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式2 若∠ACD =∠B,CD ⊥AB,△ACB 为直角
三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.课堂练习 变式3 如图,若∠C =90°,∠AED =∠B,△ADE
是直角三角形吗?为什么? 是.
有两个角互余的三角形
是直角三角形.
(证明过程略).课堂小结(1)本节课学习了哪些主要内容?
(2)你是如何探索直角三角形的性质与判定的?它们
是怎么叙述的?它们有什么区别与联系?
(3)利用直角三角形的性质与判定分别可以解决哪些
问题?布置作业教科书习题11.2第4、10题.
