【同步备课】第八单元 第1课时 数与代数-小数乘除法(课件)五年级数学上册人教版(共37张PPT)
文档属性
| 名称 | 【同步备课】第八单元 第1课时 数与代数-小数乘除法(课件)五年级数学上册人教版(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 08:45:14 | ||
图片预览










文档简介
(共37张PPT)
总复习
8
人教版五年级数学上册
第1课时 小数乘、除法
回顾教材第1、3单元的内容,想一想,在这两个单元中我们学习了小数乘、除法的哪些知识?
小组交流、讨论。
计算
法则
小
数
乘
除
法
转化
小数点定位
小数乘法
整数乘法
小数除法
除数是整数的除法
小数乘法:
根据因数的小数位数确定积的小数点的位置
除数是整数的小数除法:
商的小数点与被除数的小数点对齐
除数是小数的小数除法:
商的小数点与被除数移动后的小数点对齐
意义
小数乘整数:与整整乘法的意义完全相同,求几个几相加是多少。
小数乘小数:(整数部分是0)求一个数的十分之几、百分之几、千分之几……(整数部分不是0)求一个数的几倍是多少。
小数除法的意义:与整数除法意义相同,已知两个因数的积与其中一个因数,求另一个因数的运算.
小
数
乘
除
法
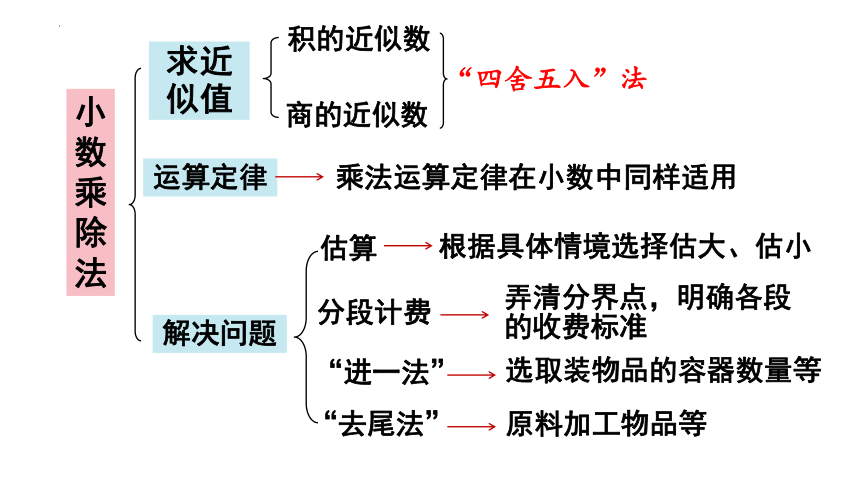
运算定律
解决问题
乘法运算定律在小数中同样适用
估算
分段计费
“进一法”
“去尾法”
根据具体情境选择估大、估小
弄清分界点,明确各段的收费标准
选取装物品的容器数量等
原料加工物品等
求近
似值
“四舍五入”法
积的近似数
商的近似数
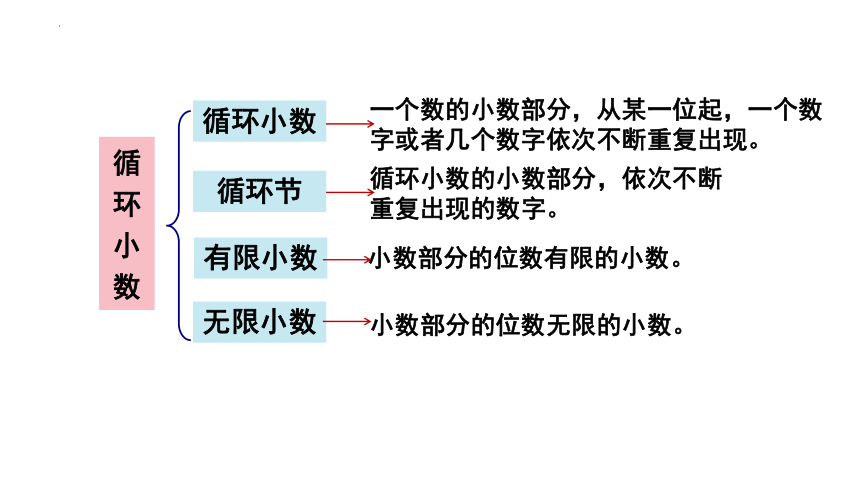
循环小数
循环小数
一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现。
循环节
循环小数的小数部分,依次不断重复出现的数字。
有限小数
小数部分的位数有限的小数。
无限小数
小数部分的位数无限的小数。
小数乘、除法的意义
例: 8.4×15
84×1.5
84×0.15
表示: 15个8.4是多少
表示: 84的1.5倍是多少
表示: 84的百分之十五是多少
表示:已知两个因数的积是79.2,
其中一个因数是6,另一个因数是多少.
表示:已知两个因数的积是3.6,
其中一个因数是0.9,另一个因数是多少.
例:79.2÷6
3.6÷0.9
5 3 3 0
2.0 5
× 2.6
1 2 3 0
.
先按照整数乘法计算,因数中有几位小数,积中也应有几位小数。
如果积的末尾有0,要先点上小数点,再将0舍去,化简。
4 1 0
2.05×2.6=
5.33
乘法怎么验算呢?
小数乘、除法的计算
可以交换两个因数的位置再乘一遍,也可以用学过的小数除法进行验算。
11.5÷0.28
除数是小数的计算方法:
(2)按整数除法的方法去除;
(3)商的小数点要和被除数的小数点对齐;
(4)整数部分不够除,商0,点上小数点;
(5)如果有余数,要添0再除。
0.144÷0.16
11.5
0.28
(1)用商不变定律,扩大相同倍数;
0
1150
28
0.144
0.16
14.4
16
小数乘、除法的计算
7.65÷0.85=
扩大到它的100倍
85
7 65
扩大到它的100倍
9
0.
.
.
.
9
7 65
0
把除数变成整数,被除数和除数同时扩大相同的倍数.
除法怎么验算呢?
用被除数除以商,看是否等于除数,或用除数与商相乘,看是否等于被除数。
小数乘、除法的计算
除法中的变化规律
①商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商 。
②除数不变,被除数扩大,商 。
③被除数不变,除数缩小,商 。
不变
扩大
扩大
一个数(0除外)除以大于1的数,商比被除数___。
一个数(0除外)除以小于1(0除外)的数,商比被除数____。
计算:
27×3= , 24÷6= 。
2.7×3= , 2.4÷6= 。
2.7×0.3= , 2.4÷0.6= 。
2.7×0.03= ,2.4÷0.06= 。
81
4
8.1
0.4
0.81
4
0.081
40
你发现什么规律了吗?
小
大
规律:一个数(0除外)乘大于1的数,积比原来的数大;
一个数(0除外)乘小于1的数,积比原来的数小。
(教材第113页第1<1>题)
积和因数、商和被除数的关系
0.25×0.49×8
3.6+4.4×1.8
(先乘后加)
(乘法交换律)
1.下面各题怎样简便就怎样算。
= 3.6 +7.92
= 11.52
=0.25×8×0.49
= 2×0.49
=0.98
4.2×7.8+2.2×4.2
63×1.01
(乘法分配律)
= 4.2 ×(7.8+2.2)
=4.2×10
=42
=63×(0.01+1)
= 63×0.01+63×1
=0.63+63
=63.63
小数的运算顺序和整数的运算顺序
一样:先算乘除,再算加减。
整数运算定律和运算性质适用于小数。
小数乘法和除法的运算顺序和运算定律
2.根据我们学过的运算定律,在下面的□里填上合适的数,在○里填上合适的运算符号。
(教材第112页第3题)
31.8× =1.2 ×
(2.5+3.5)× = × ○ ×4
(1.5×1.2)× =1.2×( ×6)
1.2
31.8
4
2.5
3.5
4
1.5
6
+
整数乘法的交换律、结合律和分配律对小数乘法同样适用。利用这些运算定律可以使一些计算简便。
小数乘法和除法的运算顺序和运算定律
4.6÷11的商的小数部分第138位上的数字是( )。
9
2
.
4.6
0
8
0
4 4
4
11
1 1
1
8 8
2
0
0
1
9
1 1
4.6÷11
= 0.41818…
1
商0.41818…的循环节是18,即从百分位起18依次不断重复出现。
(138-1)÷2=66……1,余数是1。
第138位上的数字就是循环节的第1位数字“1”。
循环小数及其应用
循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现。
循环节:循环小数依次不断重复出现的那几个数字。
循环小数的简便写法:写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个小圆点。
循环小数及其应用
有限小数:小数部分的位数有限的小数。
例如,0.9375是一个有限小数。
无限小数:小数部分的位数无限的小数。
例如, 就是一个无限小数。
0.2142857
小数
有限小数
无限小数
循环小数
循环小数及其应用
1.林华的妈妈去市场买水果。她先花10元买了2.5 kg 橙子,还准备买3 kg 苹果,苹果的单价是橙子的1.6 倍。
橙子单价:10÷2.5 = 4(元/kg)
苹果单价: 4×1.6 = 6.4(元/kg)
苹果总价: 6.4×3 = 13.2(元)
答:买苹果应付13.2元。
买苹果应付多少钱?
(教材第110页第1<2>题)
先求橙子的单价。
再求苹果的单价。
最后求苹果的总价。
用小数乘除法解决实际问题
2.从地球上向月球发射的一个激光信号,经过约2.56秒收到从月球反射回来的信号。已知光速是30万千米/秒,算一算这时测试点到月球表面的距离约是多少。
30×2.56÷2= 38.4(万千米)
答:这时月球到地球的距离是38.4万千米。
用小数乘除法解决实际问题
(教材第114页第16题)
1.30元钱买下面的东西够吗?和同桌说一说你是怎么算的。
一共估成3元
估成4元
一共估成10元
用估算解决实际问题
3+4+10=17(元)
17元<30元
答:够买下面这些物品。
要判断“够”的话,所有的数据都要估大或不变;
一共估成3元
估成4元
一共估成10元
用估算解决实际问题
2.一个房间长8.1 m,宽5.2 m。 现在要铺上边长为0.6 m的正 方形地砖,100块够吗?(不考虑损耗。)
比较房间的面积和100块地砖面积的大小。
(1)解决“100块够吗”这个问题,就是要比较哪两个面积的大小?
用估算解决实际问题
面积小于或等于100块地砖的总面积,就够,反之就不够。
2.一个房间长8.1 m,宽5.2 m。 现在要铺上边长为0.6 m的正 方形地砖,100块够吗?(不考虑损耗。)
(2)怎样比较房间面积和100块地砖面积的大小?
方法一:100×0.6×0.6=36(m2)
8.1×5.2≈40(m2)
36<40
答:100块这样的地砖不够。
方法二:8.1×5.2÷(0.6×0.6)
=42.12÷0.36
=117(块)
100<117
答:100块这样的地砖不够。
用估算解决实际问题
用估算解决实际问题时:
要判断“够”的话,所有的数据都要估大或不变;
要判断“不够”的话,所有的数据都要估小或不变。
估的时候要注意估大或估小要适度,要能解决问题。
用估算解决实际问题
方法:
阅读与理解:找出数量关系。
分析与解答:根据实际数据选择适当的估算策略。
回顾与反思:通过对比不同的方法,明确要根据实际问题和数据选择适当的估算策略。
1. 四川省峨眉山是我国降雨天数最多的地方。峨眉山的年降水量可达2033.9mm,平均每月降水量大约有多少毫米?(得数保留一位小数)
2033.9÷12 ≈ 169.5(mm)
答:平均每月降水量大约有169.5毫米。
(教材第113页第5题)
根据“年降水量÷12=月降水量”列式。
按“四舍五入”法取近似数。
根据实际情况取近似数
铁桶:21÷0.8=26.25≈26(个)
包装箱:26÷4=6.5≈7(个)
去尾法
进一法
2.每制造一个铁桶需要0.8平方米的铁皮,
(1)21平方米的铁皮最多能做多少个这样的铁桶?
(2)如果每个包装箱最多能装这样的铁桶4个,至少需要多少个包装箱?
根据实际情况取近似数
进一法:就是在保留整数时,无论十分位上是多少,一律往整数部分进一(如容器装东西)。
去尾法:就是在保留整数时,无论十分位上是多少,一律去掉(如材料做东西)。
根据实际情况取近似数
根据实际情况,求近似数的方法一般有三种:
四舍五入法 , 进一法 , 去尾法。
1. 王阿姨的车在某停车场停了5.3小时,需付多少元?
某停车场收费标准
(1)2小时内(含2小时)5元;
(2)超过2小时的部分,每小时1.5元(不足1小时的按1小时计算)。
5 + 4×1.5=11(元)
答:需付11元。
停车超过2小时,所以要分段计费。
前2小时要付5元,后3.3小时按4小时计算。每小时1.5元。
分段计费问题
2. 某市出租车收费规定如下:乘车路程不超过2km时,收费8元(起步价);超过2km时,超过部分按每千米2.5元加收车费(不足1km按1km计算)。詹阿姨某次乘车付车费18元,她乘车一共的路程最多是多少千米?
答:她乘车一共的路程最多是6千米。
这是一道分段计费的逆向应用题。
(18-8)÷2.5+2=6(km)
先把车费分作两部分:起步8元和超出部分(18-8)元。
求出超出部分的里程。
最后求总路程。
注意:解答分段计费问题,要弄清分界点,明确每一段的收费标准,也可以借助表格分析或用假设法解决。
分段计费问题
(1)分段计算法:把每个阶段按其标准分别计算, 最后求和。
(2)假设调整法:先按照一个阶段的标准计算,再加上或减去多计算的,就是要求的费用。
1.填空。
(1)计算小数乘除法时,要转化成( )乘除法来计算。
(2)计算小数乘法时,如果积的小数位数不够,就在积的前面添( )补位;如果乘得的积末尾有0,根据小数的性质,应该把0 ( )。
整 数
0
去掉
(3)计算小数除法时,商的小数点要与( )的小数点( ),有余数时,可在余数后面补( )继续除。
被除数
对齐
0
(4)一本漫画书3.65元,丁丁要买5本,就是求( )个( )是多少,也可以说( )的( )倍是多少。 列式是( )。
5
3.65
3.65 × 5
5
3.65
(5)一个数的7倍是38.5,求这个数。列式为( ),结果是( )
38.5÷7
5.5
(6)小芳用0.45小时做了9朵红花,她平均每小时做( )朵红花,平均做1朵红花要( )小时。
(7)粮店里每个油桶最多装4.5 kg油,要装60 kg油,至少需要准备( )个这样的油桶。
20
0.05
14
(8)0.47×7.5的积是( )位小数,5.6÷0.02的商的最高位在( )位上。
(9)4.19393…可以简写成( ),保留一位小数约是( )。
(10)两数相除的商是26.7,余数是0.3,如果被除数和除数同时扩大10倍,那么商是( ),余数是( )。
(11)一个两位小数,保留一位小数后约是3.2,这个两位小数最大是( ),最小是( )。
(12)在 里填上“>”、“<”或“=”。
3.45×0.99 3.45 3.45÷0.99 3.45
三
百
4.2
26.7
3
3.24
3.15
<
>
(1)如果两个数相除的商小于被除数,那么除数( )。
A.大于1 B.小于1 C.等于1
(2)3.2323… 的循环节是( )。
A.23 B.32 C.2323
(3)A÷0.4=B×0.4,A、B两数都不为0 ,则A、B两数的大小关系是( )。
A.A>B B.A(4)2.83÷0.27=10.481481…,这个商用简便记法写作( )。
A
A
B
2.选择
A 10.48148
B 10.48
C 10.481
C
3. 判断
(1)7.32626…是循环小数。 ( )
(2)0.48÷0.8+0.2=0.48÷(0.8+0.2)=0.48 ( )
(3)在被除数不为0的除法中,除数大于0且小于1,商就大于被除数。 ( )
(4)两个小数相乘的积一定大于1。 ( )
4. 在下面的○里填上“>”或“<”。
9.9×6.9○70 0.97×23.8○24 57.5×6.2○420
15.6×2.1○30 26.4×1.08○26.4 5.9×7.8○48
<
<
<
<
>
>
我是先计算,再作比较。
(教材第114页第15题)
我是先估算一下左边的积,利用估大法或估小法直接判定结果。
5.判断用进一法还是用去尾法。
(1)国庆节五(1)班16名同学到世界之窗游玩,每3名同学一条船,需几条船?
(2)夏铭用彩纸折叠纸飞机,每5张纸折一架,34张纸可以折几架?
进一法
去尾法
5.判断用进一法还是用去尾法。
去尾法
进一法
(3)一种圆珠笔2.5元钱一支,12元钱最多能买几支?
(4)校办工厂把1010个乒乓球装箱,每20个装一纸箱,需要多少个纸箱?
总复习
8
人教版五年级数学上册
第1课时 小数乘、除法
回顾教材第1、3单元的内容,想一想,在这两个单元中我们学习了小数乘、除法的哪些知识?
小组交流、讨论。
计算
法则
小
数
乘
除
法
转化
小数点定位
小数乘法
整数乘法
小数除法
除数是整数的除法
小数乘法:
根据因数的小数位数确定积的小数点的位置
除数是整数的小数除法:
商的小数点与被除数的小数点对齐
除数是小数的小数除法:
商的小数点与被除数移动后的小数点对齐
意义
小数乘整数:与整整乘法的意义完全相同,求几个几相加是多少。
小数乘小数:(整数部分是0)求一个数的十分之几、百分之几、千分之几……(整数部分不是0)求一个数的几倍是多少。
小数除法的意义:与整数除法意义相同,已知两个因数的积与其中一个因数,求另一个因数的运算.
小
数
乘
除
法
运算定律
解决问题
乘法运算定律在小数中同样适用
估算
分段计费
“进一法”
“去尾法”
根据具体情境选择估大、估小
弄清分界点,明确各段的收费标准
选取装物品的容器数量等
原料加工物品等
求近
似值
“四舍五入”法
积的近似数
商的近似数
循环小数
循环小数
一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现。
循环节
循环小数的小数部分,依次不断重复出现的数字。
有限小数
小数部分的位数有限的小数。
无限小数
小数部分的位数无限的小数。
小数乘、除法的意义
例: 8.4×15
84×1.5
84×0.15
表示: 15个8.4是多少
表示: 84的1.5倍是多少
表示: 84的百分之十五是多少
表示:已知两个因数的积是79.2,
其中一个因数是6,另一个因数是多少.
表示:已知两个因数的积是3.6,
其中一个因数是0.9,另一个因数是多少.
例:79.2÷6
3.6÷0.9
5 3 3 0
2.0 5
× 2.6
1 2 3 0
.
先按照整数乘法计算,因数中有几位小数,积中也应有几位小数。
如果积的末尾有0,要先点上小数点,再将0舍去,化简。
4 1 0
2.05×2.6=
5.33
乘法怎么验算呢?
小数乘、除法的计算
可以交换两个因数的位置再乘一遍,也可以用学过的小数除法进行验算。
11.5÷0.28
除数是小数的计算方法:
(2)按整数除法的方法去除;
(3)商的小数点要和被除数的小数点对齐;
(4)整数部分不够除,商0,点上小数点;
(5)如果有余数,要添0再除。
0.144÷0.16
11.5
0.28
(1)用商不变定律,扩大相同倍数;
0
1150
28
0.144
0.16
14.4
16
小数乘、除法的计算
7.65÷0.85=
扩大到它的100倍
85
7 65
扩大到它的100倍
9
0.
.
.
.
9
7 65
0
把除数变成整数,被除数和除数同时扩大相同的倍数.
除法怎么验算呢?
用被除数除以商,看是否等于除数,或用除数与商相乘,看是否等于被除数。
小数乘、除法的计算
除法中的变化规律
①商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商 。
②除数不变,被除数扩大,商 。
③被除数不变,除数缩小,商 。
不变
扩大
扩大
一个数(0除外)除以大于1的数,商比被除数___。
一个数(0除外)除以小于1(0除外)的数,商比被除数____。
计算:
27×3= , 24÷6= 。
2.7×3= , 2.4÷6= 。
2.7×0.3= , 2.4÷0.6= 。
2.7×0.03= ,2.4÷0.06= 。
81
4
8.1
0.4
0.81
4
0.081
40
你发现什么规律了吗?
小
大
规律:一个数(0除外)乘大于1的数,积比原来的数大;
一个数(0除外)乘小于1的数,积比原来的数小。
(教材第113页第1<1>题)
积和因数、商和被除数的关系
0.25×0.49×8
3.6+4.4×1.8
(先乘后加)
(乘法交换律)
1.下面各题怎样简便就怎样算。
= 3.6 +7.92
= 11.52
=0.25×8×0.49
= 2×0.49
=0.98
4.2×7.8+2.2×4.2
63×1.01
(乘法分配律)
= 4.2 ×(7.8+2.2)
=4.2×10
=42
=63×(0.01+1)
= 63×0.01+63×1
=0.63+63
=63.63
小数的运算顺序和整数的运算顺序
一样:先算乘除,再算加减。
整数运算定律和运算性质适用于小数。
小数乘法和除法的运算顺序和运算定律
2.根据我们学过的运算定律,在下面的□里填上合适的数,在○里填上合适的运算符号。
(教材第112页第3题)
31.8× =1.2 ×
(2.5+3.5)× = × ○ ×4
(1.5×1.2)× =1.2×( ×6)
1.2
31.8
4
2.5
3.5
4
1.5
6
+
整数乘法的交换律、结合律和分配律对小数乘法同样适用。利用这些运算定律可以使一些计算简便。
小数乘法和除法的运算顺序和运算定律
4.6÷11的商的小数部分第138位上的数字是( )。
9
2
.
4.6
0
8
0
4 4
4
11
1 1
1
8 8
2
0
0
1
9
1 1
4.6÷11
= 0.41818…
1
商0.41818…的循环节是18,即从百分位起18依次不断重复出现。
(138-1)÷2=66……1,余数是1。
第138位上的数字就是循环节的第1位数字“1”。
循环小数及其应用
循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现。
循环节:循环小数依次不断重复出现的那几个数字。
循环小数的简便写法:写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末位数字上面各记一个小圆点。
循环小数及其应用
有限小数:小数部分的位数有限的小数。
例如,0.9375是一个有限小数。
无限小数:小数部分的位数无限的小数。
例如, 就是一个无限小数。
0.2142857
小数
有限小数
无限小数
循环小数
循环小数及其应用
1.林华的妈妈去市场买水果。她先花10元买了2.5 kg 橙子,还准备买3 kg 苹果,苹果的单价是橙子的1.6 倍。
橙子单价:10÷2.5 = 4(元/kg)
苹果单价: 4×1.6 = 6.4(元/kg)
苹果总价: 6.4×3 = 13.2(元)
答:买苹果应付13.2元。
买苹果应付多少钱?
(教材第110页第1<2>题)
先求橙子的单价。
再求苹果的单价。
最后求苹果的总价。
用小数乘除法解决实际问题
2.从地球上向月球发射的一个激光信号,经过约2.56秒收到从月球反射回来的信号。已知光速是30万千米/秒,算一算这时测试点到月球表面的距离约是多少。
30×2.56÷2= 38.4(万千米)
答:这时月球到地球的距离是38.4万千米。
用小数乘除法解决实际问题
(教材第114页第16题)
1.30元钱买下面的东西够吗?和同桌说一说你是怎么算的。
一共估成3元
估成4元
一共估成10元
用估算解决实际问题
3+4+10=17(元)
17元<30元
答:够买下面这些物品。
要判断“够”的话,所有的数据都要估大或不变;
一共估成3元
估成4元
一共估成10元
用估算解决实际问题
2.一个房间长8.1 m,宽5.2 m。 现在要铺上边长为0.6 m的正 方形地砖,100块够吗?(不考虑损耗。)
比较房间的面积和100块地砖面积的大小。
(1)解决“100块够吗”这个问题,就是要比较哪两个面积的大小?
用估算解决实际问题
面积小于或等于100块地砖的总面积,就够,反之就不够。
2.一个房间长8.1 m,宽5.2 m。 现在要铺上边长为0.6 m的正 方形地砖,100块够吗?(不考虑损耗。)
(2)怎样比较房间面积和100块地砖面积的大小?
方法一:100×0.6×0.6=36(m2)
8.1×5.2≈40(m2)
36<40
答:100块这样的地砖不够。
方法二:8.1×5.2÷(0.6×0.6)
=42.12÷0.36
=117(块)
100<117
答:100块这样的地砖不够。
用估算解决实际问题
用估算解决实际问题时:
要判断“够”的话,所有的数据都要估大或不变;
要判断“不够”的话,所有的数据都要估小或不变。
估的时候要注意估大或估小要适度,要能解决问题。
用估算解决实际问题
方法:
阅读与理解:找出数量关系。
分析与解答:根据实际数据选择适当的估算策略。
回顾与反思:通过对比不同的方法,明确要根据实际问题和数据选择适当的估算策略。
1. 四川省峨眉山是我国降雨天数最多的地方。峨眉山的年降水量可达2033.9mm,平均每月降水量大约有多少毫米?(得数保留一位小数)
2033.9÷12 ≈ 169.5(mm)
答:平均每月降水量大约有169.5毫米。
(教材第113页第5题)
根据“年降水量÷12=月降水量”列式。
按“四舍五入”法取近似数。
根据实际情况取近似数
铁桶:21÷0.8=26.25≈26(个)
包装箱:26÷4=6.5≈7(个)
去尾法
进一法
2.每制造一个铁桶需要0.8平方米的铁皮,
(1)21平方米的铁皮最多能做多少个这样的铁桶?
(2)如果每个包装箱最多能装这样的铁桶4个,至少需要多少个包装箱?
根据实际情况取近似数
进一法:就是在保留整数时,无论十分位上是多少,一律往整数部分进一(如容器装东西)。
去尾法:就是在保留整数时,无论十分位上是多少,一律去掉(如材料做东西)。
根据实际情况取近似数
根据实际情况,求近似数的方法一般有三种:
四舍五入法 , 进一法 , 去尾法。
1. 王阿姨的车在某停车场停了5.3小时,需付多少元?
某停车场收费标准
(1)2小时内(含2小时)5元;
(2)超过2小时的部分,每小时1.5元(不足1小时的按1小时计算)。
5 + 4×1.5=11(元)
答:需付11元。
停车超过2小时,所以要分段计费。
前2小时要付5元,后3.3小时按4小时计算。每小时1.5元。
分段计费问题
2. 某市出租车收费规定如下:乘车路程不超过2km时,收费8元(起步价);超过2km时,超过部分按每千米2.5元加收车费(不足1km按1km计算)。詹阿姨某次乘车付车费18元,她乘车一共的路程最多是多少千米?
答:她乘车一共的路程最多是6千米。
这是一道分段计费的逆向应用题。
(18-8)÷2.5+2=6(km)
先把车费分作两部分:起步8元和超出部分(18-8)元。
求出超出部分的里程。
最后求总路程。
注意:解答分段计费问题,要弄清分界点,明确每一段的收费标准,也可以借助表格分析或用假设法解决。
分段计费问题
(1)分段计算法:把每个阶段按其标准分别计算, 最后求和。
(2)假设调整法:先按照一个阶段的标准计算,再加上或减去多计算的,就是要求的费用。
1.填空。
(1)计算小数乘除法时,要转化成( )乘除法来计算。
(2)计算小数乘法时,如果积的小数位数不够,就在积的前面添( )补位;如果乘得的积末尾有0,根据小数的性质,应该把0 ( )。
整 数
0
去掉
(3)计算小数除法时,商的小数点要与( )的小数点( ),有余数时,可在余数后面补( )继续除。
被除数
对齐
0
(4)一本漫画书3.65元,丁丁要买5本,就是求( )个( )是多少,也可以说( )的( )倍是多少。 列式是( )。
5
3.65
3.65 × 5
5
3.65
(5)一个数的7倍是38.5,求这个数。列式为( ),结果是( )
38.5÷7
5.5
(6)小芳用0.45小时做了9朵红花,她平均每小时做( )朵红花,平均做1朵红花要( )小时。
(7)粮店里每个油桶最多装4.5 kg油,要装60 kg油,至少需要准备( )个这样的油桶。
20
0.05
14
(8)0.47×7.5的积是( )位小数,5.6÷0.02的商的最高位在( )位上。
(9)4.19393…可以简写成( ),保留一位小数约是( )。
(10)两数相除的商是26.7,余数是0.3,如果被除数和除数同时扩大10倍,那么商是( ),余数是( )。
(11)一个两位小数,保留一位小数后约是3.2,这个两位小数最大是( ),最小是( )。
(12)在 里填上“>”、“<”或“=”。
3.45×0.99 3.45 3.45÷0.99 3.45
三
百
4.2
26.7
3
3.24
3.15
<
>
(1)如果两个数相除的商小于被除数,那么除数( )。
A.大于1 B.小于1 C.等于1
(2)3.2323… 的循环节是( )。
A.23 B.32 C.2323
(3)A÷0.4=B×0.4,A、B两数都不为0 ,则A、B两数的大小关系是( )。
A.A>B B.A(4)2.83÷0.27=10.481481…,这个商用简便记法写作( )。
A
A
B
2.选择
A 10.48148
B 10.48
C 10.481
C
3. 判断
(1)7.32626…是循环小数。 ( )
(2)0.48÷0.8+0.2=0.48÷(0.8+0.2)=0.48 ( )
(3)在被除数不为0的除法中,除数大于0且小于1,商就大于被除数。 ( )
(4)两个小数相乘的积一定大于1。 ( )
4. 在下面的○里填上“>”或“<”。
9.9×6.9○70 0.97×23.8○24 57.5×6.2○420
15.6×2.1○30 26.4×1.08○26.4 5.9×7.8○48
<
<
<
<
>
>
我是先计算,再作比较。
(教材第114页第15题)
我是先估算一下左边的积,利用估大法或估小法直接判定结果。
5.判断用进一法还是用去尾法。
(1)国庆节五(1)班16名同学到世界之窗游玩,每3名同学一条船,需几条船?
(2)夏铭用彩纸折叠纸飞机,每5张纸折一架,34张纸可以折几架?
进一法
去尾法
5.判断用进一法还是用去尾法。
去尾法
进一法
(3)一种圆珠笔2.5元钱一支,12元钱最多能买几支?
(4)校办工厂把1010个乒乓球装箱,每20个装一纸箱,需要多少个纸箱?
