八年级数学北师大版上册 4.1 函数 课时练(含答案)
文档属性
| 名称 | 八年级数学北师大版上册 4.1 函数 课时练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 330.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 10:43:04 | ||
图片预览



文档简介
课时练
4.1 函数
一、单项选择题
1.下列各表达式不能表示y是x的函数的是( )
A.y=3x2 B.y= C.y=±(x>0) D.y=3x+1
2.下列各线中,表示y不是x的函数的是( )
3.下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积 B.正方形的周长与面积
C.等腰三角形的底边的长与面积 D.圆的周长与半径
4. 函数y=+的自变量x的取值范围是( )
A.x≥1 B.x≥1且x≠3 C.x≠3 D.1≤x≤3
5.根据如图所示程序计算函数值,若输入的x的值为,则输出的函数值为( )
A. B. C. D.
6.已知两个变量x和y,它们之间的3组对应值如下表所示:
x -1 0 1
y -1 1 3
则y与x之间的函数关系式可能是( )
A.y=2x+1 B.y=x C.y=x2+x+1 D.
7.小明从家到学校,先匀速步行到车站,等了几分钟后坐上公交车,公交车沿着公路匀速行驶了一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )
8.一辆汽车从甲地以50km/h的速度驶往乙地,已知甲地与乙地相距150km,则汽车距乙地的距离s(km)与行驶时间t(h)之间的函数解析式是( )
A.s=150+50t(t≥0) B.s=150-50t(t≤3)
C.s=150-50t(0<t<3) D.s=150-50t(0≤t≤3)
9. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部.则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
10. 万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地,假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等),又顺水航行返回万州,若该轮船从万州出发后所用的时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能够反映y与x之间函数关系的大致图象是( )
二、填空题
11.某人要在规定时间内加工100个零件,则工作效率η与时间t之间的关系中,η和t都是 (变量;常量).
12.下列变量之间的关系中,具有函数关系的有 个.
①三角形的面积与底边;②多边形的内角和与边数;③圆的面积与半径;④y=中的y与x.
13. 函数y=中,自变量x的取值范围是x 1(>; <; ≥; ≤ )
14. 函数y=中,自变量x的取值范围是 .
15.计划花500元购买篮球,所能购买的总数n(个)与单价a(元)的函数关系式为 ,其中 是自变量, 是因变量.
16.小明从家跑步到学校,接着马上原路步行回家,如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟 米.
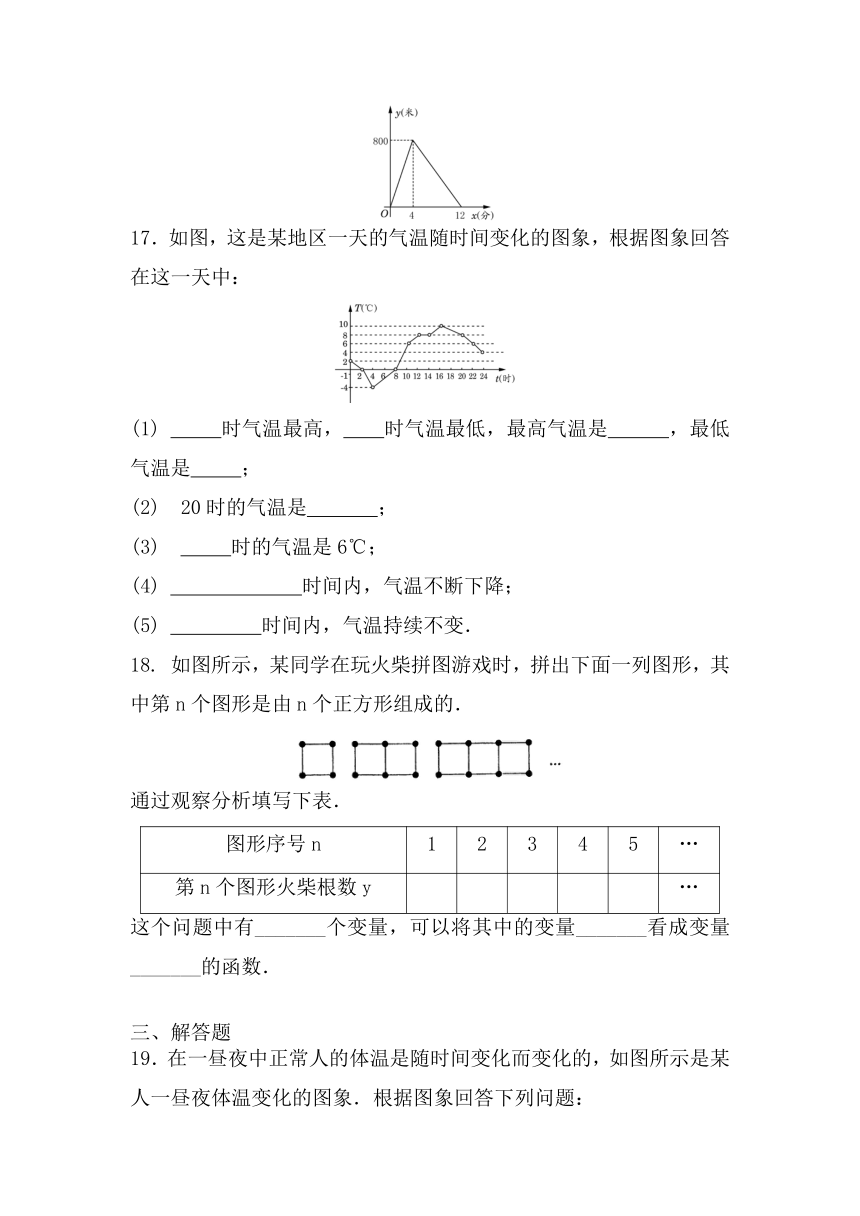
17.如图,这是某地区一天的气温随时间变化的图象,根据图象回答在这一天中:
(1) 时气温最高, 时气温最低,最高气温是 ,最低气温是 ;
(2) 20时的气温是 ;
(3) 时的气温是6℃;
(4) 时间内,气温不断下降;
(5) 时间内,气温持续不变.
18. 如图所示,某同学在玩火柴拼图游戏时,拼出下面一列图形,其中第n个图形是由n个正方形组成的.
通过观察分析填写下表.
图形序号n 1 2 3 4 5 …
第n个图形火柴根数y …
这个问题中有_______个变量,可以将其中的变量_______看成变量_______的函数.
三、解答题
19.在一昼夜中正常人的体温是随时间变化而变化的,如图所示是某人一昼夜体温变化的图象.根据图象回答下列问题:
(1)这个人的最高体温和最低体温分别是多少摄氏度?在什么时刻达到最高或最低?
(2)若用x表示时间(时),y表示体温(℃),将相应数据填入下表:
x/时 2 4 8 12 16 18 20 22
y/℃
(3)y是x的函数吗?
20.某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元(不足1千米按1千米计算),请写出出租车费y(元)与行程x(千米)之间的函数关系式.
21.星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题:
(1) 玲玲到达离家最远的地方是什么时间?离家多远?
(2) 她何时开始第一次休息?休息了多长时间?
(3) 她骑车速度最快是在什么时候?车速多少?
(4) 玲玲全程骑车的平均速度是多少?
参考答案:
一、
1-10 CCCBB ACDDC
二、
11. 变量
12. 12
13. ≥
14. x≠-3
15. n= a n
16. 100
17. (1) 16 4 10℃ -4℃
(2) 8℃
(3) 10
(4) 0~4和16~24
(5) 12~14
18. 4 7 10 13 16
两 y n
三、
19. 解:(1)18时达到最高,最高为37.5℃,0时达到最低,约为35,3℃.
(2)表格中依次填入35.5;36;37;36.5;37;37.5;37;36.5
(3)y是x的函数.
20. 解:.
21. 解:观察图象可知:(1)玲玲到达离家最远的地方是在12时,此时离家30千米;
(2)10点半时开始第一次休息,休息了半小时;
(3)玲玲郊游过程中,各时间段的速度分别为:9~10时,速度为10÷(10-9)=10(千米/小时);10~10.5时,速度约为(17.5-10)÷(10.5-10)=15(千米/小时);10.5~11时,速度为0;11~12时,速度约为(30-17.5)÷(12-11)=12.5(千米/小时);12~13时,速度为0;13~15时,在返回的途中,速度为:30÷(15-13)=15(千米/小时);可见骑行速度最快有两段时间:10~10.5时和13~15时.两段时间内的速度都是15千米/小时;
(4)玲玲全程骑车的平均速度为:(30+30)÷(15-9)=10(千米/小时).
4.1 函数
一、单项选择题
1.下列各表达式不能表示y是x的函数的是( )
A.y=3x2 B.y= C.y=±(x>0) D.y=3x+1
2.下列各线中,表示y不是x的函数的是( )
3.下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积 B.正方形的周长与面积
C.等腰三角形的底边的长与面积 D.圆的周长与半径
4. 函数y=+的自变量x的取值范围是( )
A.x≥1 B.x≥1且x≠3 C.x≠3 D.1≤x≤3
5.根据如图所示程序计算函数值,若输入的x的值为,则输出的函数值为( )
A. B. C. D.
6.已知两个变量x和y,它们之间的3组对应值如下表所示:
x -1 0 1
y -1 1 3
则y与x之间的函数关系式可能是( )
A.y=2x+1 B.y=x C.y=x2+x+1 D.
7.小明从家到学校,先匀速步行到车站,等了几分钟后坐上公交车,公交车沿着公路匀速行驶了一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )
8.一辆汽车从甲地以50km/h的速度驶往乙地,已知甲地与乙地相距150km,则汽车距乙地的距离s(km)与行驶时间t(h)之间的函数解析式是( )
A.s=150+50t(t≥0) B.s=150-50t(t≤3)
C.s=150-50t(0<t<3) D.s=150-50t(0≤t≤3)
9. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部.则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
10. 万州某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地,假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等),又顺水航行返回万州,若该轮船从万州出发后所用的时间为x(小时),轮船距万州的距离为y(千米),则下列各图中,能够反映y与x之间函数关系的大致图象是( )
二、填空题
11.某人要在规定时间内加工100个零件,则工作效率η与时间t之间的关系中,η和t都是 (变量;常量).
12.下列变量之间的关系中,具有函数关系的有 个.
①三角形的面积与底边;②多边形的内角和与边数;③圆的面积与半径;④y=中的y与x.
13. 函数y=中,自变量x的取值范围是x 1(>; <; ≥; ≤ )
14. 函数y=中,自变量x的取值范围是 .
15.计划花500元购买篮球,所能购买的总数n(个)与单价a(元)的函数关系式为 ,其中 是自变量, 是因变量.
16.小明从家跑步到学校,接着马上原路步行回家,如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟 米.
17.如图,这是某地区一天的气温随时间变化的图象,根据图象回答在这一天中:
(1) 时气温最高, 时气温最低,最高气温是 ,最低气温是 ;
(2) 20时的气温是 ;
(3) 时的气温是6℃;
(4) 时间内,气温不断下降;
(5) 时间内,气温持续不变.
18. 如图所示,某同学在玩火柴拼图游戏时,拼出下面一列图形,其中第n个图形是由n个正方形组成的.
通过观察分析填写下表.
图形序号n 1 2 3 4 5 …
第n个图形火柴根数y …
这个问题中有_______个变量,可以将其中的变量_______看成变量_______的函数.
三、解答题
19.在一昼夜中正常人的体温是随时间变化而变化的,如图所示是某人一昼夜体温变化的图象.根据图象回答下列问题:
(1)这个人的最高体温和最低体温分别是多少摄氏度?在什么时刻达到最高或最低?
(2)若用x表示时间(时),y表示体温(℃),将相应数据填入下表:
x/时 2 4 8 12 16 18 20 22
y/℃
(3)y是x的函数吗?
20.某市出租车起步价是7元(路程小于或等于2千米),超过2千米每增加1千米加收1.6元(不足1千米按1千米计算),请写出出租车费y(元)与行程x(千米)之间的函数关系式.
21.星期天,玲玲骑自行车到郊外游玩,她离家的距离与时间的关系如图所示,请根据图象回答下列问题:
(1) 玲玲到达离家最远的地方是什么时间?离家多远?
(2) 她何时开始第一次休息?休息了多长时间?
(3) 她骑车速度最快是在什么时候?车速多少?
(4) 玲玲全程骑车的平均速度是多少?
参考答案:
一、
1-10 CCCBB ACDDC
二、
11. 变量
12. 12
13. ≥
14. x≠-3
15. n= a n
16. 100
17. (1) 16 4 10℃ -4℃
(2) 8℃
(3) 10
(4) 0~4和16~24
(5) 12~14
18. 4 7 10 13 16
两 y n
三、
19. 解:(1)18时达到最高,最高为37.5℃,0时达到最低,约为35,3℃.
(2)表格中依次填入35.5;36;37;36.5;37;37.5;37;36.5
(3)y是x的函数.
20. 解:.
21. 解:观察图象可知:(1)玲玲到达离家最远的地方是在12时,此时离家30千米;
(2)10点半时开始第一次休息,休息了半小时;
(3)玲玲郊游过程中,各时间段的速度分别为:9~10时,速度为10÷(10-9)=10(千米/小时);10~10.5时,速度约为(17.5-10)÷(10.5-10)=15(千米/小时);10.5~11时,速度为0;11~12时,速度约为(30-17.5)÷(12-11)=12.5(千米/小时);12~13时,速度为0;13~15时,在返回的途中,速度为:30÷(15-13)=15(千米/小时);可见骑行速度最快有两段时间:10~10.5时和13~15时.两段时间内的速度都是15千米/小时;
(4)玲玲全程骑车的平均速度为:(30+30)÷(15-9)=10(千米/小时).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
