苏教版(2019)高中数学必修第一册 7.1 角与弧度【导学案教师版】
文档属性
| 名称 | 苏教版(2019)高中数学必修第一册 7.1 角与弧度【导学案教师版】 |  | |
| 格式 | doc | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 10:50:07 | ||
图片预览




文档简介
第7章 三角函数
第01讲 角与弧度
课程标准 重难点
理解任意角的概念;掌握象限角和终边相同的角的集合表示;会表示终边相同的角;理解并掌握象限角及其应用.理解弧度制的概念;掌握角度制与弧度制的换算;会利用弧度制表示角;会利用扇形的弧长公式及面积公式解决实际问题. 1. 理解并掌握正角、负角、零角、象限角、终边相同的角、弧度制的概念及表示.2. 认识集合中、的准确含义,明确终边相同的角不一定相等,终边相同的角有无限多个,它们相差的整数倍.掌握角度与弧度的换算公式并能熟练进行角度与弧度的换算.
一、任意角
1.角的概念
有关概念 描 述
定义 角可以看成平面内① 绕着② 从一个位置 ③ 到另一个位置所成的④
图示 其中O为⑤ ,OA为⑥ ,OB为⑦
记法 角或,或简记为
2.角的分类:按旋转方向可将角分为如下三类:
类型 定义 图示
正角 按⑧ 旋转形成的角
负角 按⑨ 旋转形成的角
零角 一条射线⑩ ,称它形成了一个零角
3.象限角与轴线角:在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
象限角: 在第几象限就是第几象限角;
轴线角:终边落在坐标轴上的角.
4.终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合 ,即任一与角α终边相同的角,都可以表示成角α与整数个的和.
二、弧度制
1. 角的单位制
(1)角度制:规定周角的为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制:把长度等于 ① 的弧所对的 ② 叫做1弧度的角.以弧度作为单位来度量角的单位制,叫做
③ ,它的单位符号是rad,读作 ④ ,通常略去不写.
(3)角的弧度数的求法:正角的弧度数是一个 ⑤ ,负角的弧度数是一个 ⑥ ,零角的弧度数是.如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值|α|= ⑦ .
2.角度与弧度的换算
角度化弧度 弧度化角度
360°= ⑧ 2π rad=360°
180°= ⑨ π rad= ⑩
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
3.弧度制下的弧长与扇形面积公式
公式度量制 弧长公式 扇形面积公式
角度制 l= S=
弧度制 l= S=
参考答案
一、①一条射线 ②端点 ③旋转 ④图形 ⑤顶点 ⑥始边 ⑦终边 ⑧逆时针方向 ⑨顺时针方向
⑩没有作任何旋转 终边 {β|β=α+k·360°,k∈Z} 周角
二、①半径长 ②圆心角 ③弧度制 ④弧度 ⑤正数
⑥负数 ⑦ ⑧2πrad ⑨πrad ⑩180°
|α|·r lr=|α|r2
考法01 任意角
引入任意角的概念后需要注意:
(1)用“旋转”定义角之后,角的范围大大地扩大了.角的概念推广以后,它包括任意大小的正角、负角和零角.
(2)角的概念的理解要紧紧抓住“旋转”二字,用运动的观点来看待角的概念:一是要明确旋转的方向,二是要明确旋转的大小,三是要明确射线作任何旋转时的位置.
(3)角的范围不再限于.
(4)当角的始边相同时,若角相等,则终边相同;终边相同,而角不一定相等.
(5)要正确理解正角、负角、零角的概念,由定义可知,关键是抓住终边的旋转方向是逆时针、顺时针,还是没有转动.在图中表示角时,应注意箭头的方向不可丢掉,箭头方向代表角的正负.
(6)角的记法:用一个希腊字母表示,如,,,…;也可用三个大写的英文字母表示,字母前要写符号“”,中间的字母表示角的顶点,如,,….为了简单起见,在不引起混淆的前提下,“角”或“”可以简记为“”.
(7)引入正角、负角、零角后,角的减法可以转化为角的加法运算,即可以转化为.
1.喜洋洋步行从家里到草原学校去上学,一般需要10分钟,则10分钟时间,钟表的分针走过的角度是( )
A. B. C. D.
【跟踪训练】1.(1)时钟走了3小时20分,则时针所转过的角的度数为 ,分针转过的角的度数为 .
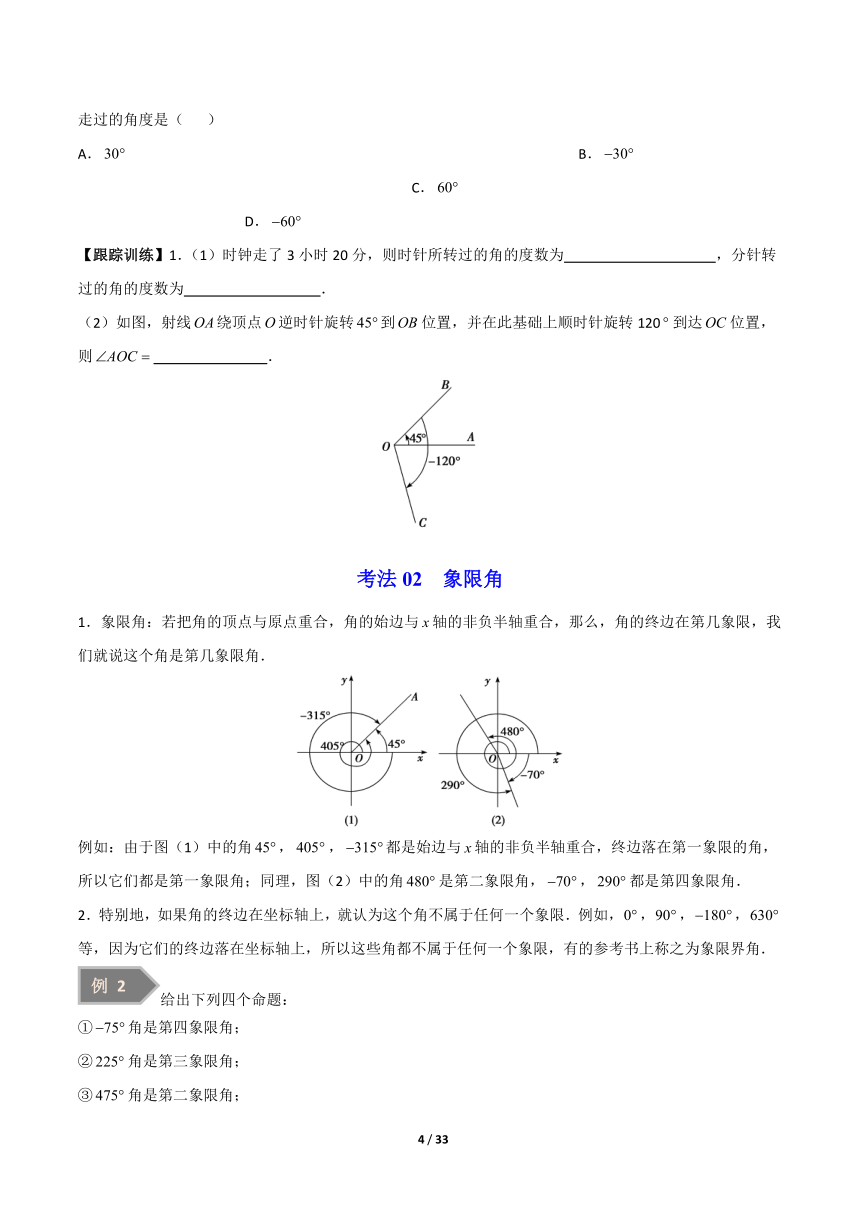
(2)如图,射线绕顶点逆时针旋转到位置,并在此基础上顺时针旋转120到达位置,则 .
考法02 象限角
1.象限角:若把角的顶点与原点重合,角的始边与轴的非负半轴重合,那么,角的终边在第几象限,我们就说这个角是第几象限角.
例如:由于图(1)中的角,,都是始边与轴的非负半轴重合,终边落在第一象限的角,所以它们都是第一象限角;同理,图(2)中的角是第二象限角,,都是第四象限角.
2.特别地,如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.例如,,,,等,因为它们的终边落在坐标轴上,所以这些角都不属于任何一个象限,有的参考书上称之为象限界角.
给出下列四个命题:
①角是第四象限角;
②角是第三象限角;
③角是第二象限角;
④角是第一象限角;
⑤角是第四象限角.
其中正确的命题的个数是( )
A.2 B.3 C.4 D.5
【跟踪训练】
判断下列各角分别是第几象限角:,,,45,,,,,,,,.
考法03 终边相同的角
1.一般地,我们有:所有与角终边相同的角,连同角在内,可构成一个集合,,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
2.象限角的分类及表示方法如下:
象限角 集合的表示
第一象限角
第二象限角
第三象限角
第四象限角
3.设,显然,所有与角终边相同的角都是集合的元素;反过来,集合中的任何一个元素也都与角的终边相同.推广到一般形式有:所有与角终边相同的角,连同角在内,可构成一个集合,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
4.利用与角终边相同的角的集合,可把任意角转化成,,的形式;也可利用与角终边相同的角化简终边落在过原点的某一条直线上的角的集合;或利用与角终边相同的角写出各象限角和象限界角的集合.
如第一象限角,在~360范围内,第一象限角表示为,然后在两端加上,,即可得到第一象限角的集合:,,其他各象限角同理可得.
若为象限界角,如终边落在轴的负半轴上,代表角为180,所以终边落在轴的负半轴上的角的集合为,.同理可得其他非象限角的集合.
已知.
(1)把写成,的形式,并指出它是第几象限角;
(2)求,使与的终边相同,且.
【跟踪训练】与角终边相同的角的集合是( )
A.,
B.,
C.,
D.,
考法04 角度与弧度之间的互化
1.将角度化为弧度
rad;rad;rad.
2.将弧度化为角度
;;.
3.需记住的特殊角的度数与弧度数的对应值
度
弧度 0
【说明】(1)以弧度为单位表示角时,“弧度”两字可以省略不写.如是指sin(2弧度);是指弧度.以度为单位表示角时,度就不能省去.
(2)以弧度为单位表示角时,常常把弧度数写成多少的形式,如无特殊要求,不必把化成小数,如弧度,不必写成弧度.
(3)弧度制和角度制一样,都是一种度量角的单位制.弧度制与角度制相比有一定的优点,其一体现在进位上,角度制在度、分、秒上是六十进制,不便于计算,而弧度制是十进制,给运算带来了方便;其二体现在弧长公式与扇形面积公式的表达上,弧度制下的公式比角度制下的公式简单,运用起来更方便.
(4)用角度制和弧度制来度量零角,虽然单位不同,但数量相同,对于其他非零角,由于单位不同,数量也就不同了.
(5)在进行角度与弧度的换算时,抓住关系式rad是关键,由它可以得到:角度弧度,弧度角度.
1.将下列角度与弧度进行互化:
(1);(2);(3);(4).
【跟踪训练】(1)化为弧度是( )
A. B. C. D.
(2)化为角度是( )
A. B. C. D.
考法05 弧长与面积公式
1.弧长公式
在半径为的圆中,弧长为的弧所对的圆心角大小为,则,变形可得,此公式称为弧长公式,其中的是弧度角.
2.扇形面积公式
因为圆心角为1 rad的扇形面积为,而弧长为l的扇形的圆心角大小为rad,所以其面积为,将代入上式可得,此公式称为扇形面积公式.
3.弧长公式及扇形面积公式的两种表示
角度制 弧度制
弧长公式
扇形面积公式
注意事项 是扇形的半径,是圆心角的角度数 是扇形的半径,是圆心角的弧度数,是弧长
显然弧度制下的两个公式在形式上都要简单的多,记忆和应用也就更加方便.
已知一个扇形的周长为,圆心角为,求这个扇形的面积.
【解题技巧】求扇形面积的关键是求得扇形的圆心角、半径、弧长三个量中的任意两个量.相反,也可由扇形的面积结合其他条件,求扇形的圆心角、半径、弧长.解题时要注意公式的灵活变形及方程思想的运用.
【跟踪训练】直径为20 cm的圆中,求弧度为的圆心角所对的弧长及该扇形的面积.
题组A 基础过关练
1.已知扇形的弧长为,圆心角为,则该扇形的面积为( )
A. B. C. D.
2.“数摺聚清风,一捻生秋意”是宋朝朱翌描写折扇的诗句,折扇出人怀袖,扇面书画,扇骨雕琢,是文人雅士的宠物,所以又有“怀袖雅物”的别号.如图是折扇的示意图,其中OA=20cm,∠AOB=120°,M为OA的中点,则扇面(图中扇环)部分的面积是( )
A.cm2 B.cm2 C.cm2 D.cm2
3.与终边相同的角是( )
A. B.170° C.20° D.340°
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A.120° B.135° C.150° D.165°
5.装饰公司制作一种扇形板状装饰品,其圆心角为,并在扇形弧上正面等距安装7个发彩光的小灯泡且在背面用导线将小灯泡串连(弧的两端各一个灯泡,导线接头忽略不计),已知扇形的半径为30厘米,则连接导线大致需要的长度约为( )
A.55厘米 B.63厘米 C.69厘米 D.76厘米
6.密位制是度量角的一种方法.把一周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位的单位制叫做密位制.在角的密位制中,采用4个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数和十位数之间画一条短线连接(不足100密位的角用0补全百位和十位),例如7密位写成“”,2021密位写成“”,1周角等于6000密位,记作“”.如果一个半径为2的扇形的面积为,则其圆心角用密位制表示为( )
A. B. C. D.
7.密位制是度量角的一种方法.将周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数字与十位数字之间画一条短线,如:478密位写成“4-78”,1周角等于6000密位,记作1周角.如果一个扇形的半径为2,面积为,则其圆心角可以用密位制表示为( )
A.25-00 B.35-00 C.42-00 D.70-00
8.刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当n很大时,用圆内接正边形的周长近似等于圆周长,并计算出精确度很高的圆周率.在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想.运用此思想,当取时,可得的近似值为( )
A. B. C. D.
题组B 能力提升练
1.中国传统折扇文化有着极其深厚的底蕴,一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形(如图)的面积为,圆心角为,圆面中剩余部分的面积为,圆心角为,当与的比值为(黄金分割比)时,折扇看上去较为美观,那么( )
A. B. C. D.
2.下列说法错误的是( )
A.第二象限角比第一象限角大
B.角与角是终边相同角
C.钝角一定是第二象限角
D.将表的分针拨慢10分钟,则分针转过的角的弧度数为
3.关于角度,下列说法正确的是( )
A.时钟经过两个小时,时针转过的角度是
B.钝角大于锐角
C.三角形的内角必是第一或第二象限角
D.若是第二象限角,则是第一或第三象限角
4.如图,扇形的圆心角为,半径为,记弓形的面积为,扇形的面积为,则______.
5.折扇是一种用竹木做扇骨,韧纸或绫绢做扇面的能折叠的扇子.用时须展开,成扇形,聚头散尾.如图,某折扇的扇骨长度,扇面长度,已知折扇展开所对圆心角的弧度为,则扇面的面积为___________.
6.与终边相同的最小正角是___________.
7.在与角终边相同的角中,求满足下列条件的角.
(1)最小的正角;
(2)最大的负角;
(3)内的角.
8.将下列角度化为弧度,弧度转化为角度
(1),(2),(3),(4),(5),(6).
题组C 培优拔尖练
1.若是第二象限的角,则的终边所在位置可能是( )
A.第一象限 B.第二象限
C.第三象限 D.笫四象限
2.下列命题中正确的是( )
A.若角是第三象限角,则可能在第三象限
B.
C.若且,则为第二象限角
D.锐角终边上一点坐标为,则
3.在北纬圈上有甲、乙两地,若它们在纬度圈上的弧长等于(为地球半径),则这两地间的球面距离为_______ .
4.如图,已知长为,宽为的长方形在桌面上作无滑动翻滚,翻滚到第四次时被小木块挡住,此时长方形的底边与桌面所成的角为,求点走过的路程及走过的弧所在扇形的总面积.
5.一只红蚂蚁与一只黑蚂蚁在一个圆(半径为的圆)的圆周上爬动,且两只蚂蚁均从点同时逆时针匀速爬动,红蚂蚁每秒爬过角,黑蚂蚁每秒爬过角(其中).如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限.
(1)求,的值.
(2)两只蚂蚁的爬行速度保持不变,若红蚂蚁从点A逆时针匀速爬行,黑蚂蚁同时从点A顺时针匀速爬行,求当它们从点A出发后第一次相遇时,红蚂蚁爬过的距离.
6.已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=10 cm,求扇形的弧长l;
(2)已知扇形的周长为10 cm,面积是4 cm2,求扇形的圆心角;
(3)若扇形周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
第7章 三角函数
第01讲 不等式的性质答案
课程标准 重难点
理解任意角的概念;掌握象限角和终边相同的角的集合表示;会表示终边相同的角;理解并掌握象限角及其应用.理解弧度制的概念;掌握角度制与弧度制的换算;会利用弧度制表示角;会利用扇形的弧长公式及面积公式解决实际问题. 1. 理解并掌握正角、负角、零角、象限角、终边相同的角、弧度制的概念及表示.2. 认识集合中、的准确含义,明确终边相同的角不一定相等,终边相同的角有无限多个,它们相差的整数倍.掌握角度与弧度的换算公式并能熟练进行角度与弧度的换算.
一、任意角
1.角的概念
有关概念 描 述
定义 角可以看成平面内① 绕着② 从一个位置 ③ 到另一个位置所成的④
图示 其中O为⑤ ,OA为⑥ ,OB为⑦
记法 角或,或简记为
2.角的分类:按旋转方向可将角分为如下三类:
类型 定义 图示
正角 按⑧ 旋转形成的角
负角 按⑨ 旋转形成的角
零角 一条射线⑩ ,称它形成了一个零角
3.象限角与轴线角:在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
象限角: 在第几象限就是第几象限角;
轴线角:终边落在坐标轴上的角.
4.终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合 ,即任一与角α终边相同的角,都可以表示成角α与整数个的和.
二、弧度制
1. 角的单位制
(1)角度制:规定周角的为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制:把长度等于 ① 的弧所对的 ② 叫做1弧度的角.以弧度作为单位来度量角的单位制,叫做
③ ,它的单位符号是rad,读作 ④ ,通常略去不写.
(3)角的弧度数的求法:正角的弧度数是一个 ⑤ ,负角的弧度数是一个 ⑥ ,零角的弧度数是.如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值|α|= ⑦ .
2.角度与弧度的换算
角度化弧度 弧度化角度
360°= ⑧ 2π rad=360°
180°= ⑨ π rad= ⑩
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
3.弧度制下的弧长与扇形面积公式
公式度量制 弧长公式 扇形面积公式
角度制 l= S=
弧度制 l= S=
参考答案
一、①一条射线 ②端点 ③旋转 ④图形 ⑤顶点 ⑥始边 ⑦终边 ⑧逆时针方向 ⑨顺时针方向
⑩没有作任何旋转 终边 {β|β=α+k·360°,k∈Z} 周角
二、①半径长 ②圆心角 ③弧度制 ④弧度 ⑤正数
⑥负数 ⑦ ⑧2πrad ⑨πrad ⑩180°
|α|·r lr=|α|r2
考法01 任意角
引入任意角的概念后需要注意:
(1)用“旋转”定义角之后,角的范围大大地扩大了.角的概念推广以后,它包括任意大小的正角、负角和零角.
(2)角的概念的理解要紧紧抓住“旋转”二字,用运动的观点来看待角的概念:一是要明确旋转的方向,二是要明确旋转的大小,三是要明确射线作任何旋转时的位置.
(3)角的范围不再限于.
(4)当角的始边相同时,若角相等,则终边相同;终边相同,而角不一定相等.
(5)要正确理解正角、负角、零角的概念,由定义可知,关键是抓住终边的旋转方向是逆时针、顺时针,还是没有转动.在图中表示角时,应注意箭头的方向不可丢掉,箭头方向代表角的正负.
(6)角的记法:用一个希腊字母表示,如,,,…;也可用三个大写的英文字母表示,字母前要写符号“”,中间的字母表示角的顶点,如,,….为了简单起见,在不引起混淆的前提下,“角”或“”可以简记为“”.
(7)引入正角、负角、零角后,角的减法可以转化为角的加法运算,即可以转化为.
1.喜洋洋步行从家里到草原学校去上学,一般需要10分钟,则10分钟时间,钟表的分针走过的角度是( )
A. B. C. D.
【思路分析】分针60分钟走一圈→计算出分针1分钟走的度数→计算出分针10分钟走的度数→注意角度的正负.
【答案】D
【解析】利用定义,分针是顺时针走的,形成的角度是负角,
又周角为,所以有,
即分针走过的角度是.
故选D.
【跟踪训练】1.(1)时钟走了3小时20分,则时针所转过的角的度数为 ,分针转过的角的度数为 .
(2)如图,射线绕顶点逆时针旋转到位置,并在此基础上顺时针旋转120到达位置,则 .
【思路分析】(1)计算出指针单位时间内走过的度数→乘以时间.
(2)→→
【答案】(1) (2)
【解析】(1)从时针和分针每小时或每分钟转过的角度数切入,时针每小时转,分针每小时转,每分钟转、时针、分针都按顺时针方向旋转,故转过的角度数都是负的,3小时20分即小时,故时针转过的角度数为;分针转过的角度数为.
(2)由角的定义可得.
考法02 象限角
1.象限角:若把角的顶点与原点重合,角的始边与轴的非负半轴重合,那么,角的终边在第几象限,我们就说这个角是第几象限角.
例如:由于图(1)中的角,,都是始边与轴的非负半轴重合,终边落在第一象限的角,所以它们都是第一象限角;同理,图(2)中的角是第二象限角,,都是第四象限角.
2.特别地,如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.例如,,,,等,因为它们的终边落在坐标轴上,所以这些角都不属于任何一个象限,有的参考书上称之为象限界角.
给出下列四个命题:
①角是第四象限角;
②角是第三象限角;
③角是第二象限角;
④角是第一象限角;
⑤角是第四象限角.
其中正确的命题的个数是( )
A.2 B.3 C.4 D.5
【思路分析】把已知角写成→用象限角的概念判断.
【答案】C
【解析】利用象限角的概念来判断.
先把已知角写成的形式,
再判断是第几象限角,
从而确定是第几象限角.
所以①②③④都对.
的角的终边在轴的非正半轴上,
所以角不是第四象限角.
因此⑤是不正确的.
所以正确的命题的个数是4.
故选C.
【跟踪训练】
判断下列各角分别是第几象限角:,,,45,,,,,,,,.
【思路分析】把已知角写成→用象限角的概念判断.
【解析】45,,是第一象限角;
,,是第二象限角;
,,是第三象限角;
,,是第四象限角.
考法03 终边相同的角
1.一般地,我们有:所有与角终边相同的角,连同角在内,可构成一个集合,,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
2.象限角的分类及表示方法如下:
象限角 集合的表示
第一象限角
第二象限角
第三象限角
第四象限角
3.设,显然,所有与角终边相同的角都是集合的元素;反过来,集合中的任何一个元素也都与角的终边相同.推广到一般形式有:所有与角终边相同的角,连同角在内,可构成一个集合,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
4.利用与角终边相同的角的集合,可把任意角转化成,,的形式;也可利用与角终边相同的角化简终边落在过原点的某一条直线上的角的集合;或利用与角终边相同的角写出各象限角和象限界角的集合.
如第一象限角,在~360范围内,第一象限角表示为,然后在两端加上,,即可得到第一象限角的集合:,,其他各象限角同理可得.
若为象限界角,如终边落在轴的负半轴上,代表角为180,所以终边落在轴的负半轴上的角的集合为,.同理可得其他非象限角的集合.
已知.
(1)把写成,的形式,并指出它是第几象限角;
(2)求,使与的终边相同,且.
【思路分析】用所给角除以,将余数作为即可.注意负角除以时,为保证余数为正角,试商时应使得到的负角的绝对值大于已知负角的绝对值.
【解析】(1)∵余,
∴,
∴相应的,是第三象限角.
∴是第三象限角.
(2)令,
取,,
则,.
∴与的终边相同,且适合的角为角,角.
【跟踪训练】与角终边相同的角的集合是( )
A.,
B.,
C.,
D.,
【思路分析】用所给角除以,将余数作为即可.注意负角除以时,为保证余数为正角.
【答案】C
【解析】题目考查终边相同的角的表示方法,可用特殊值法研究,也可用定义分析解决,由,可得给论为C,或者由角与角终边相同,角与角终边相同,角应与角终边相同,故应选C.
考法04 角度与弧度之间的互化
1.将角度化为弧度
rad;rad;rad.
2.将弧度化为角度
;;.
3.需记住的特殊角的度数与弧度数的对应值
度
弧度 0
【说明】(1)以弧度为单位表示角时,“弧度”两字可以省略不写.如是指sin(2弧度);是指弧度.以度为单位表示角时,度就不能省去.
(2)以弧度为单位表示角时,常常把弧度数写成多少的形式,如无特殊要求,不必把化成小数,如弧度,不必写成弧度.
(3)弧度制和角度制一样,都是一种度量角的单位制.弧度制与角度制相比有一定的优点,其一体现在进位上,角度制在度、分、秒上是六十进制,不便于计算,而弧度制是十进制,给运算带来了方便;其二体现在弧长公式与扇形面积公式的表达上,弧度制下的公式比角度制下的公式简单,运用起来更方便.
(4)用角度制和弧度制来度量零角,虽然单位不同,但数量相同,对于其他非零角,由于单位不同,数量也就不同了.
(5)在进行角度与弧度的换算时,抓住关系式rad是关键,由它可以得到:角度弧度,弧度角度.
1.将下列角度与弧度进行互化:
(1);(2);(3);(4).
【思路分析】利用公式1°= rad或1 rad=进行换算.
【解析】(1);
(2);
(3);
(4).
【跟踪训练】(1)化为弧度是( )
A. B. C. D.
(2)化为角度是( )
A. B. C. D.
【思路分析】利用公式1°= rad或1 rad=进行换算.
【答案】B C
【解析】(1)∵rad,
∴.故选B.
(2)∵1 rad,
∴ rad,故选C.
考法05 弧长与面积公式
1.弧长公式
在半径为的圆中,弧长为的弧所对的圆心角大小为,则,变形可得,此公式称为弧长公式,其中的是弧度角.
2.扇形面积公式
因为圆心角为1 rad的扇形面积为,而弧长为l的扇形的圆心角大小为rad,所以其面积为,将代入上式可得,此公式称为扇形面积公式.
3.弧长公式及扇形面积公式的两种表示
角度制 弧度制
弧长公式
扇形面积公式
注意事项 是扇形的半径,是圆心角的角度数 是扇形的半径,是圆心角的弧度数,是弧长
显然弧度制下的两个公式在形式上都要简单的多,记忆和应用也就更加方便.
已知一个扇形的周长为,圆心角为,求这个扇形的面积.
【思路分析】先根据扇形的周长等于弧长加两个半径长列出方程,求出半径的长度,再用扇形的面积公式计算.
【解析】设扇形的半径为,面积为,
则扇形的圆心角为.
∴扇形的弧长为,
∴,
∴.
∴.
即扇形的面积为.
【解题技巧】求扇形面积的关键是求得扇形的圆心角、半径、弧长三个量中的任意两个量.相反,也可由扇形的面积结合其他条件,求扇形的圆心角、半径、弧长.解题时要注意公式的灵活变形及方程思想的运用.
【跟踪训练】直径为20 cm的圆中,求弧度为的圆心角所对的弧长及该扇形的面积.
【思路分析】先用弧长公式求出弧长,再用扇形的面积公式求出扇形的面积.
【解析】因为直径为20 cm,
所以cm,
又,
所以弧长(cm),
面积().
题组A 基础过关练
1.已知扇形的弧长为,圆心角为,则该扇形的面积为( )
A. B. C. D.
【答案】B
【解析】扇形的圆心角为,弧长为,
扇形的半径,
扇形的面积.
故选:B.
2.“数摺聚清风,一捻生秋意”是宋朝朱翌描写折扇的诗句,折扇出人怀袖,扇面书画,扇骨雕琢,是文人雅士的宠物,所以又有“怀袖雅物”的别号.如图是折扇的示意图,其中OA=20cm,∠AOB=120°,M为OA的中点,则扇面(图中扇环)部分的面积是( )
A.cm2 B.cm2 C.cm2 D.cm2
【答案】B
【解析】扇环的面积为.
故选:B
3.与终边相同的角是( )
A. B.170° C.20° D.340°
【答案】D
【解析】与终边相同的角一定可以写成的形式,,
令 可得,与终边相同,其它选项均不合题意,故选:.
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A.120° B.135° C.150° D.165°
【答案】C
【解析】一日十二个时辰,则一个时辰所对应的圆心角为,丑时与午时相差个时辰,故丑时与午时的夹角为
故选:C
5.装饰公司制作一种扇形板状装饰品,其圆心角为,并在扇形弧上正面等距安装7个发彩光的小灯泡且在背面用导线将小灯泡串连(弧的两端各一个灯泡,导线接头忽略不计),已知扇形的半径为30厘米,则连接导线大致需要的长度约为( )
A.55厘米 B.63厘米 C.69厘米 D.76厘米
【答案】B
【解析】因为在弧长比较短的情况下分成6等份,每部分的弦长和弧长相差很小,
所以可以用弧长近似代替弦长,
所以导线的长度为(厘米).故选:B
6.密位制是度量角的一种方法.把一周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位的单位制叫做密位制.在角的密位制中,采用4个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数和十位数之间画一条短线连接(不足100密位的角用0补全百位和十位),例如7密位写成“”,2021密位写成“”,1周角等于6000密位,记作“”.如果一个半径为2的扇形的面积为,则其圆心角用密位制表示为( )
A. B. C. D.
【答案】B
【解析】设扇形半径为r,圆心角为,则扇形面积为,
则,则其表示的密位为,即17-50.故选:B
7.密位制是度量角的一种方法.将周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数字与十位数字之间画一条短线,如:478密位写成“4-78”,1周角等于6000密位,记作1周角.如果一个扇形的半径为2,面积为,则其圆心角可以用密位制表示为( )
A.25-00 B.35-00 C.42-00 D.70-00
【答案】B
【解析】设扇形的圆心角为,则,则,
由题意可知,其密位大小为密位,用密位制表示为35-00.故选:B.
8.刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当n很大时,用圆内接正边形的周长近似等于圆周长,并计算出精确度很高的圆周率.在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想.运用此思想,当取时,可得的近似值为( )
A. B. C. D.
【答案】D
【解析】将一个单位圆分成个扇形,则每个扇形的圆心角度数均为
由圆的垂径定理,可得每个圆心角所对的弦长,
因为这个扇形对应的弦长之和近似于单位圆的周长,
所以,
所以.
故选:D.
题组B 能力提升练
1.中国传统折扇文化有着极其深厚的底蕴,一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形(如图)的面积为,圆心角为,圆面中剩余部分的面积为,圆心角为,当与的比值为(黄金分割比)时,折扇看上去较为美观,那么( )
A. B. C. D.
【答案】BCD
【解析】设扇形的半径为,由,故D正确;
由,
所以,解得,故C正确;
由,则,
所以,
所以,故B正确.故选:BCD
2.下列说法错误的是( )
A.第二象限角比第一象限角大
B.角与角是终边相同角
C.钝角一定是第二象限角
D.将表的分针拨慢10分钟,则分针转过的角的弧度数为
【答案】AB
【解析】A中,第二象限角比第一象限角大不正确,如是第二象限角,是第一象限角;
B中,因为,所以角与角终边不同,故错误;
C中,因为钝角的范围为,所以钝角是第二象限角,故正确;
D中,将表的分针拨慢10分钟,则分针转过的角的弧度数为正确.故选:AB
3.关于角度,下列说法正确的是( )
A.时钟经过两个小时,时针转过的角度是
B.钝角大于锐角
C.三角形的内角必是第一或第二象限角
D.若是第二象限角,则是第一或第三象限角
【答案】BD
【解析】对于A,时钟经过两个小时,时针转过的角是,故错误;
对于B,钝角一定大于锐角,显然正确;
对于C,若三角形的内角为,是终边在轴正半轴上的角,故错误;
对于D,角的终边在第二象限,
,,
,
当为偶数时,,,得是第一象限角;
当为奇数时,,,得是第三象限角,故正确.故选:BD
4.如图,扇形的圆心角为,半径为,记弓形的面积为,扇形的面积为,则______.
【答案】
【解析】扇形的面积,
弓形的面积,
则,
故答案为:.
5.折扇是一种用竹木做扇骨,韧纸或绫绢做扇面的能折叠的扇子.用时须展开,成扇形,聚头散尾.如图,某折扇的扇骨长度,扇面长度,已知折扇展开所对圆心角的弧度为,则扇面的面积为___________.
【答案】
【解析】由题可知,扇面的面积为.故答案为:.
6.与终边相同的最小正角是___________.
【答案】
【解析】因为,所以与终边相同的最小正角是.故答案为:.
7.在与角终边相同的角中,求满足下列条件的角.
(1)最小的正角;
(2)最大的负角;
(3)内的角.
【答案】(1);(2);(3)、、、.
【解析】
和终边相同
其余的终边相同的角度可以写成
(1)当时是最小的正角,;
(2)当时是最大的负角,;
(3)当,,0,1时,、、、符合条件.
8.将下列角度化为弧度,弧度转化为角度
(1),(2),(3),(4),(5),(6).
【答案】(1);(2);(3);(4);(5);(6).
【解析】(1)弧度弧度,
(2)弧度弧度,
(3)弧度弧度.
(4)弧度,
(5)弧度,
(6)弧度.
题组C 培优拔尖练
1.若是第二象限的角,则的终边所在位置可能是( )
A.第一象限 B.第二象限
C.第三象限 D.笫四象限
【答案】ABD
【解析】是第二象限的角,则,,
,,
当时,是第一象限角,
当时,是第二象限角,
当时,是第四象限角,故选:ABD.
2.下列命题中正确的是( )
A.若角是第三象限角,则可能在第三象限
B.
C.若且,则为第二象限角
D.锐角终边上一点坐标为,则
【答案】ACD
【解析】对于,角是第三象限角,即,所以,当时, 为第一象限角; 当时, 为第三象限角; 当时, 为第四象限角,故可能在第三象限正确,故选项正确.
对于,运用诱导公式化简,故选项不正确.
对于,若,则为第二象限角或者第四象限角,若,则为第一象限角或者第二象限角,同时满足且,则为第二象限角,故选项正确.
对于,因为锐角终边上一点坐标为,由三角函数定义可得,又因为,所以,故选项正确.综上选项正确.故选
3.在北纬圈上有甲、乙两地,若它们在纬度圈上的弧长等于(为地球半径),则这两地间的球面距离为_______ .
【答案】
【解析】设甲、乙两地分别为,
北纬圈所在圆的半径为,
它们在纬度圈上所对应的劣弧长等于(为地球半径),
(是两地在北纬60圈上对应的圆心角),
故.
所以线段
设地球的中心为,则是等边三角形,
所以,
故这两地的球面距离是.
4.如图,已知长为,宽为的长方形在桌面上作无滑动翻滚,翻滚到第四次时被小木块挡住,此时长方形的底边与桌面所成的角为,求点走过的路程及走过的弧所在扇形的总面积.
【答案】, .
【解析】如图:
在扇形中,圆心角为,
弧长,
面积.
在扇形中,圆心角为,
弧长,
面积,
在扇形中,圆心角为,
弧长,
面积.
综上,点走过的路程,
点走过的弧所在扇形的总面积.
5.一只红蚂蚁与一只黑蚂蚁在一个圆(半径为的圆)的圆周上爬动,且两只蚂蚁均从点同时逆时针匀速爬动,红蚂蚁每秒爬过角,黑蚂蚁每秒爬过角(其中).如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限.
(1)求,的值.
(2)两只蚂蚁的爬行速度保持不变,若红蚂蚁从点A逆时针匀速爬行,黑蚂蚁同时从点A顺时针匀速爬行,求当它们从点A出发后第一次相遇时,红蚂蚁爬过的距离.
【答案】(1),;(2).
【解析】(1)由题意可得,与都是的整数倍,
不妨设,,
则,,
又两只蚂蚁在第2秒时均位于第二象限,
所以,即,所以,
因为,所以,所以,,
即,;
(2)两只蚂蚁的爬行速度保持不变,若红蚂蚁从点A逆时针匀速爬行,黑蚂蚁同时从点A顺时针匀速爬行,设它们从点A出发后第一次相遇时,所用的时间为秒,
则,即,解得,
所以红蚂蚁爬过的角度为,
因为圆的半径为,
所以红蚂蚁爬过的距离为.
6.已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=10 cm,求扇形的弧长l;
(2)已知扇形的周长为10 cm,面积是4 cm2,求扇形的圆心角;
(3)若扇形周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
【解析】(1)α=60°=rad,∴l=α·R=×10= (cm).
(2)由题意得解得 (舍去),
故扇形圆心角为.
(3)由已知得,l+2R=20.
所以S=lR= (20-2R)R=10R-R2=-(R-5)2+25,所以当R=5时,S取得最大值25,此时l=10,α=2.
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
例4
例5
分层提分
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
例4
例5
分层提分
2 / 2
第01讲 角与弧度
课程标准 重难点
理解任意角的概念;掌握象限角和终边相同的角的集合表示;会表示终边相同的角;理解并掌握象限角及其应用.理解弧度制的概念;掌握角度制与弧度制的换算;会利用弧度制表示角;会利用扇形的弧长公式及面积公式解决实际问题. 1. 理解并掌握正角、负角、零角、象限角、终边相同的角、弧度制的概念及表示.2. 认识集合中、的准确含义,明确终边相同的角不一定相等,终边相同的角有无限多个,它们相差的整数倍.掌握角度与弧度的换算公式并能熟练进行角度与弧度的换算.
一、任意角
1.角的概念
有关概念 描 述
定义 角可以看成平面内① 绕着② 从一个位置 ③ 到另一个位置所成的④
图示 其中O为⑤ ,OA为⑥ ,OB为⑦
记法 角或,或简记为
2.角的分类:按旋转方向可将角分为如下三类:
类型 定义 图示
正角 按⑧ 旋转形成的角
负角 按⑨ 旋转形成的角
零角 一条射线⑩ ,称它形成了一个零角
3.象限角与轴线角:在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
象限角: 在第几象限就是第几象限角;
轴线角:终边落在坐标轴上的角.
4.终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合 ,即任一与角α终边相同的角,都可以表示成角α与整数个的和.
二、弧度制
1. 角的单位制
(1)角度制:规定周角的为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制:把长度等于 ① 的弧所对的 ② 叫做1弧度的角.以弧度作为单位来度量角的单位制,叫做
③ ,它的单位符号是rad,读作 ④ ,通常略去不写.
(3)角的弧度数的求法:正角的弧度数是一个 ⑤ ,负角的弧度数是一个 ⑥ ,零角的弧度数是.如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值|α|= ⑦ .
2.角度与弧度的换算
角度化弧度 弧度化角度
360°= ⑧ 2π rad=360°
180°= ⑨ π rad= ⑩
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
3.弧度制下的弧长与扇形面积公式
公式度量制 弧长公式 扇形面积公式
角度制 l= S=
弧度制 l= S=
参考答案
一、①一条射线 ②端点 ③旋转 ④图形 ⑤顶点 ⑥始边 ⑦终边 ⑧逆时针方向 ⑨顺时针方向
⑩没有作任何旋转 终边 {β|β=α+k·360°,k∈Z} 周角
二、①半径长 ②圆心角 ③弧度制 ④弧度 ⑤正数
⑥负数 ⑦ ⑧2πrad ⑨πrad ⑩180°
|α|·r lr=|α|r2
考法01 任意角
引入任意角的概念后需要注意:
(1)用“旋转”定义角之后,角的范围大大地扩大了.角的概念推广以后,它包括任意大小的正角、负角和零角.
(2)角的概念的理解要紧紧抓住“旋转”二字,用运动的观点来看待角的概念:一是要明确旋转的方向,二是要明确旋转的大小,三是要明确射线作任何旋转时的位置.
(3)角的范围不再限于.
(4)当角的始边相同时,若角相等,则终边相同;终边相同,而角不一定相等.
(5)要正确理解正角、负角、零角的概念,由定义可知,关键是抓住终边的旋转方向是逆时针、顺时针,还是没有转动.在图中表示角时,应注意箭头的方向不可丢掉,箭头方向代表角的正负.
(6)角的记法:用一个希腊字母表示,如,,,…;也可用三个大写的英文字母表示,字母前要写符号“”,中间的字母表示角的顶点,如,,….为了简单起见,在不引起混淆的前提下,“角”或“”可以简记为“”.
(7)引入正角、负角、零角后,角的减法可以转化为角的加法运算,即可以转化为.
1.喜洋洋步行从家里到草原学校去上学,一般需要10分钟,则10分钟时间,钟表的分针走过的角度是( )
A. B. C. D.
【跟踪训练】1.(1)时钟走了3小时20分,则时针所转过的角的度数为 ,分针转过的角的度数为 .
(2)如图,射线绕顶点逆时针旋转到位置,并在此基础上顺时针旋转120到达位置,则 .
考法02 象限角
1.象限角:若把角的顶点与原点重合,角的始边与轴的非负半轴重合,那么,角的终边在第几象限,我们就说这个角是第几象限角.
例如:由于图(1)中的角,,都是始边与轴的非负半轴重合,终边落在第一象限的角,所以它们都是第一象限角;同理,图(2)中的角是第二象限角,,都是第四象限角.
2.特别地,如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.例如,,,,等,因为它们的终边落在坐标轴上,所以这些角都不属于任何一个象限,有的参考书上称之为象限界角.
给出下列四个命题:
①角是第四象限角;
②角是第三象限角;
③角是第二象限角;
④角是第一象限角;
⑤角是第四象限角.
其中正确的命题的个数是( )
A.2 B.3 C.4 D.5
【跟踪训练】
判断下列各角分别是第几象限角:,,,45,,,,,,,,.
考法03 终边相同的角
1.一般地,我们有:所有与角终边相同的角,连同角在内,可构成一个集合,,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
2.象限角的分类及表示方法如下:
象限角 集合的表示
第一象限角
第二象限角
第三象限角
第四象限角
3.设,显然,所有与角终边相同的角都是集合的元素;反过来,集合中的任何一个元素也都与角的终边相同.推广到一般形式有:所有与角终边相同的角,连同角在内,可构成一个集合,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
4.利用与角终边相同的角的集合,可把任意角转化成,,的形式;也可利用与角终边相同的角化简终边落在过原点的某一条直线上的角的集合;或利用与角终边相同的角写出各象限角和象限界角的集合.
如第一象限角,在~360范围内,第一象限角表示为,然后在两端加上,,即可得到第一象限角的集合:,,其他各象限角同理可得.
若为象限界角,如终边落在轴的负半轴上,代表角为180,所以终边落在轴的负半轴上的角的集合为,.同理可得其他非象限角的集合.
已知.
(1)把写成,的形式,并指出它是第几象限角;
(2)求,使与的终边相同,且.
【跟踪训练】与角终边相同的角的集合是( )
A.,
B.,
C.,
D.,
考法04 角度与弧度之间的互化
1.将角度化为弧度
rad;rad;rad.
2.将弧度化为角度
;;.
3.需记住的特殊角的度数与弧度数的对应值
度
弧度 0
【说明】(1)以弧度为单位表示角时,“弧度”两字可以省略不写.如是指sin(2弧度);是指弧度.以度为单位表示角时,度就不能省去.
(2)以弧度为单位表示角时,常常把弧度数写成多少的形式,如无特殊要求,不必把化成小数,如弧度,不必写成弧度.
(3)弧度制和角度制一样,都是一种度量角的单位制.弧度制与角度制相比有一定的优点,其一体现在进位上,角度制在度、分、秒上是六十进制,不便于计算,而弧度制是十进制,给运算带来了方便;其二体现在弧长公式与扇形面积公式的表达上,弧度制下的公式比角度制下的公式简单,运用起来更方便.
(4)用角度制和弧度制来度量零角,虽然单位不同,但数量相同,对于其他非零角,由于单位不同,数量也就不同了.
(5)在进行角度与弧度的换算时,抓住关系式rad是关键,由它可以得到:角度弧度,弧度角度.
1.将下列角度与弧度进行互化:
(1);(2);(3);(4).
【跟踪训练】(1)化为弧度是( )
A. B. C. D.
(2)化为角度是( )
A. B. C. D.
考法05 弧长与面积公式
1.弧长公式
在半径为的圆中,弧长为的弧所对的圆心角大小为,则,变形可得,此公式称为弧长公式,其中的是弧度角.
2.扇形面积公式
因为圆心角为1 rad的扇形面积为,而弧长为l的扇形的圆心角大小为rad,所以其面积为,将代入上式可得,此公式称为扇形面积公式.
3.弧长公式及扇形面积公式的两种表示
角度制 弧度制
弧长公式
扇形面积公式
注意事项 是扇形的半径,是圆心角的角度数 是扇形的半径,是圆心角的弧度数,是弧长
显然弧度制下的两个公式在形式上都要简单的多,记忆和应用也就更加方便.
已知一个扇形的周长为,圆心角为,求这个扇形的面积.
【解题技巧】求扇形面积的关键是求得扇形的圆心角、半径、弧长三个量中的任意两个量.相反,也可由扇形的面积结合其他条件,求扇形的圆心角、半径、弧长.解题时要注意公式的灵活变形及方程思想的运用.
【跟踪训练】直径为20 cm的圆中,求弧度为的圆心角所对的弧长及该扇形的面积.
题组A 基础过关练
1.已知扇形的弧长为,圆心角为,则该扇形的面积为( )
A. B. C. D.
2.“数摺聚清风,一捻生秋意”是宋朝朱翌描写折扇的诗句,折扇出人怀袖,扇面书画,扇骨雕琢,是文人雅士的宠物,所以又有“怀袖雅物”的别号.如图是折扇的示意图,其中OA=20cm,∠AOB=120°,M为OA的中点,则扇面(图中扇环)部分的面积是( )
A.cm2 B.cm2 C.cm2 D.cm2
3.与终边相同的角是( )
A. B.170° C.20° D.340°
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A.120° B.135° C.150° D.165°
5.装饰公司制作一种扇形板状装饰品,其圆心角为,并在扇形弧上正面等距安装7个发彩光的小灯泡且在背面用导线将小灯泡串连(弧的两端各一个灯泡,导线接头忽略不计),已知扇形的半径为30厘米,则连接导线大致需要的长度约为( )
A.55厘米 B.63厘米 C.69厘米 D.76厘米
6.密位制是度量角的一种方法.把一周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位的单位制叫做密位制.在角的密位制中,采用4个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数和十位数之间画一条短线连接(不足100密位的角用0补全百位和十位),例如7密位写成“”,2021密位写成“”,1周角等于6000密位,记作“”.如果一个半径为2的扇形的面积为,则其圆心角用密位制表示为( )
A. B. C. D.
7.密位制是度量角的一种方法.将周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数字与十位数字之间画一条短线,如:478密位写成“4-78”,1周角等于6000密位,记作1周角.如果一个扇形的半径为2,面积为,则其圆心角可以用密位制表示为( )
A.25-00 B.35-00 C.42-00 D.70-00
8.刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当n很大时,用圆内接正边形的周长近似等于圆周长,并计算出精确度很高的圆周率.在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想.运用此思想,当取时,可得的近似值为( )
A. B. C. D.
题组B 能力提升练
1.中国传统折扇文化有着极其深厚的底蕴,一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形(如图)的面积为,圆心角为,圆面中剩余部分的面积为,圆心角为,当与的比值为(黄金分割比)时,折扇看上去较为美观,那么( )
A. B. C. D.
2.下列说法错误的是( )
A.第二象限角比第一象限角大
B.角与角是终边相同角
C.钝角一定是第二象限角
D.将表的分针拨慢10分钟,则分针转过的角的弧度数为
3.关于角度,下列说法正确的是( )
A.时钟经过两个小时,时针转过的角度是
B.钝角大于锐角
C.三角形的内角必是第一或第二象限角
D.若是第二象限角,则是第一或第三象限角
4.如图,扇形的圆心角为,半径为,记弓形的面积为,扇形的面积为,则______.
5.折扇是一种用竹木做扇骨,韧纸或绫绢做扇面的能折叠的扇子.用时须展开,成扇形,聚头散尾.如图,某折扇的扇骨长度,扇面长度,已知折扇展开所对圆心角的弧度为,则扇面的面积为___________.
6.与终边相同的最小正角是___________.
7.在与角终边相同的角中,求满足下列条件的角.
(1)最小的正角;
(2)最大的负角;
(3)内的角.
8.将下列角度化为弧度,弧度转化为角度
(1),(2),(3),(4),(5),(6).
题组C 培优拔尖练
1.若是第二象限的角,则的终边所在位置可能是( )
A.第一象限 B.第二象限
C.第三象限 D.笫四象限
2.下列命题中正确的是( )
A.若角是第三象限角,则可能在第三象限
B.
C.若且,则为第二象限角
D.锐角终边上一点坐标为,则
3.在北纬圈上有甲、乙两地,若它们在纬度圈上的弧长等于(为地球半径),则这两地间的球面距离为_______ .
4.如图,已知长为,宽为的长方形在桌面上作无滑动翻滚,翻滚到第四次时被小木块挡住,此时长方形的底边与桌面所成的角为,求点走过的路程及走过的弧所在扇形的总面积.
5.一只红蚂蚁与一只黑蚂蚁在一个圆(半径为的圆)的圆周上爬动,且两只蚂蚁均从点同时逆时针匀速爬动,红蚂蚁每秒爬过角,黑蚂蚁每秒爬过角(其中).如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限.
(1)求,的值.
(2)两只蚂蚁的爬行速度保持不变,若红蚂蚁从点A逆时针匀速爬行,黑蚂蚁同时从点A顺时针匀速爬行,求当它们从点A出发后第一次相遇时,红蚂蚁爬过的距离.
6.已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=10 cm,求扇形的弧长l;
(2)已知扇形的周长为10 cm,面积是4 cm2,求扇形的圆心角;
(3)若扇形周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
第7章 三角函数
第01讲 不等式的性质答案
课程标准 重难点
理解任意角的概念;掌握象限角和终边相同的角的集合表示;会表示终边相同的角;理解并掌握象限角及其应用.理解弧度制的概念;掌握角度制与弧度制的换算;会利用弧度制表示角;会利用扇形的弧长公式及面积公式解决实际问题. 1. 理解并掌握正角、负角、零角、象限角、终边相同的角、弧度制的概念及表示.2. 认识集合中、的准确含义,明确终边相同的角不一定相等,终边相同的角有无限多个,它们相差的整数倍.掌握角度与弧度的换算公式并能熟练进行角度与弧度的换算.
一、任意角
1.角的概念
有关概念 描 述
定义 角可以看成平面内① 绕着② 从一个位置 ③ 到另一个位置所成的④
图示 其中O为⑤ ,OA为⑥ ,OB为⑦
记法 角或,或简记为
2.角的分类:按旋转方向可将角分为如下三类:
类型 定义 图示
正角 按⑧ 旋转形成的角
负角 按⑨ 旋转形成的角
零角 一条射线⑩ ,称它形成了一个零角
3.象限角与轴线角:在直角坐标系内,使角的顶点与原点重合,角的始边与x轴的非负半轴重合.
象限角: 在第几象限就是第几象限角;
轴线角:终边落在坐标轴上的角.
4.终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合 ,即任一与角α终边相同的角,都可以表示成角α与整数个的和.
二、弧度制
1. 角的单位制
(1)角度制:规定周角的为1度的角,用度作为单位来度量角的单位制叫做角度制.
(2)弧度制:把长度等于 ① 的弧所对的 ② 叫做1弧度的角.以弧度作为单位来度量角的单位制,叫做
③ ,它的单位符号是rad,读作 ④ ,通常略去不写.
(3)角的弧度数的求法:正角的弧度数是一个 ⑤ ,负角的弧度数是一个 ⑥ ,零角的弧度数是.如果半径为r的圆的圆心角α所对弧的长为l,那么角α的弧度数的绝对值|α|= ⑦ .
2.角度与弧度的换算
角度化弧度 弧度化角度
360°= ⑧ 2π rad=360°
180°= ⑨ π rad= ⑩
1°= rad≈0.017 45 rad 1 rad=°≈57.30°
3.弧度制下的弧长与扇形面积公式
公式度量制 弧长公式 扇形面积公式
角度制 l= S=
弧度制 l= S=
参考答案
一、①一条射线 ②端点 ③旋转 ④图形 ⑤顶点 ⑥始边 ⑦终边 ⑧逆时针方向 ⑨顺时针方向
⑩没有作任何旋转 终边 {β|β=α+k·360°,k∈Z} 周角
二、①半径长 ②圆心角 ③弧度制 ④弧度 ⑤正数
⑥负数 ⑦ ⑧2πrad ⑨πrad ⑩180°
|α|·r lr=|α|r2
考法01 任意角
引入任意角的概念后需要注意:
(1)用“旋转”定义角之后,角的范围大大地扩大了.角的概念推广以后,它包括任意大小的正角、负角和零角.
(2)角的概念的理解要紧紧抓住“旋转”二字,用运动的观点来看待角的概念:一是要明确旋转的方向,二是要明确旋转的大小,三是要明确射线作任何旋转时的位置.
(3)角的范围不再限于.
(4)当角的始边相同时,若角相等,则终边相同;终边相同,而角不一定相等.
(5)要正确理解正角、负角、零角的概念,由定义可知,关键是抓住终边的旋转方向是逆时针、顺时针,还是没有转动.在图中表示角时,应注意箭头的方向不可丢掉,箭头方向代表角的正负.
(6)角的记法:用一个希腊字母表示,如,,,…;也可用三个大写的英文字母表示,字母前要写符号“”,中间的字母表示角的顶点,如,,….为了简单起见,在不引起混淆的前提下,“角”或“”可以简记为“”.
(7)引入正角、负角、零角后,角的减法可以转化为角的加法运算,即可以转化为.
1.喜洋洋步行从家里到草原学校去上学,一般需要10分钟,则10分钟时间,钟表的分针走过的角度是( )
A. B. C. D.
【思路分析】分针60分钟走一圈→计算出分针1分钟走的度数→计算出分针10分钟走的度数→注意角度的正负.
【答案】D
【解析】利用定义,分针是顺时针走的,形成的角度是负角,
又周角为,所以有,
即分针走过的角度是.
故选D.
【跟踪训练】1.(1)时钟走了3小时20分,则时针所转过的角的度数为 ,分针转过的角的度数为 .
(2)如图,射线绕顶点逆时针旋转到位置,并在此基础上顺时针旋转120到达位置,则 .
【思路分析】(1)计算出指针单位时间内走过的度数→乘以时间.
(2)→→
【答案】(1) (2)
【解析】(1)从时针和分针每小时或每分钟转过的角度数切入,时针每小时转,分针每小时转,每分钟转、时针、分针都按顺时针方向旋转,故转过的角度数都是负的,3小时20分即小时,故时针转过的角度数为;分针转过的角度数为.
(2)由角的定义可得.
考法02 象限角
1.象限角:若把角的顶点与原点重合,角的始边与轴的非负半轴重合,那么,角的终边在第几象限,我们就说这个角是第几象限角.
例如:由于图(1)中的角,,都是始边与轴的非负半轴重合,终边落在第一象限的角,所以它们都是第一象限角;同理,图(2)中的角是第二象限角,,都是第四象限角.
2.特别地,如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.例如,,,,等,因为它们的终边落在坐标轴上,所以这些角都不属于任何一个象限,有的参考书上称之为象限界角.
给出下列四个命题:
①角是第四象限角;
②角是第三象限角;
③角是第二象限角;
④角是第一象限角;
⑤角是第四象限角.
其中正确的命题的个数是( )
A.2 B.3 C.4 D.5
【思路分析】把已知角写成→用象限角的概念判断.
【答案】C
【解析】利用象限角的概念来判断.
先把已知角写成的形式,
再判断是第几象限角,
从而确定是第几象限角.
所以①②③④都对.
的角的终边在轴的非正半轴上,
所以角不是第四象限角.
因此⑤是不正确的.
所以正确的命题的个数是4.
故选C.
【跟踪训练】
判断下列各角分别是第几象限角:,,,45,,,,,,,,.
【思路分析】把已知角写成→用象限角的概念判断.
【解析】45,,是第一象限角;
,,是第二象限角;
,,是第三象限角;
,,是第四象限角.
考法03 终边相同的角
1.一般地,我们有:所有与角终边相同的角,连同角在内,可构成一个集合,,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
2.象限角的分类及表示方法如下:
象限角 集合的表示
第一象限角
第二象限角
第三象限角
第四象限角
3.设,显然,所有与角终边相同的角都是集合的元素;反过来,集合中的任何一个元素也都与角的终边相同.推广到一般形式有:所有与角终边相同的角,连同角在内,可构成一个集合,即任一与角终边相同的角,都可以表示成角与整数个周角的和.
4.利用与角终边相同的角的集合,可把任意角转化成,,的形式;也可利用与角终边相同的角化简终边落在过原点的某一条直线上的角的集合;或利用与角终边相同的角写出各象限角和象限界角的集合.
如第一象限角,在~360范围内,第一象限角表示为,然后在两端加上,,即可得到第一象限角的集合:,,其他各象限角同理可得.
若为象限界角,如终边落在轴的负半轴上,代表角为180,所以终边落在轴的负半轴上的角的集合为,.同理可得其他非象限角的集合.
已知.
(1)把写成,的形式,并指出它是第几象限角;
(2)求,使与的终边相同,且.
【思路分析】用所给角除以,将余数作为即可.注意负角除以时,为保证余数为正角,试商时应使得到的负角的绝对值大于已知负角的绝对值.
【解析】(1)∵余,
∴,
∴相应的,是第三象限角.
∴是第三象限角.
(2)令,
取,,
则,.
∴与的终边相同,且适合的角为角,角.
【跟踪训练】与角终边相同的角的集合是( )
A.,
B.,
C.,
D.,
【思路分析】用所给角除以,将余数作为即可.注意负角除以时,为保证余数为正角.
【答案】C
【解析】题目考查终边相同的角的表示方法,可用特殊值法研究,也可用定义分析解决,由,可得给论为C,或者由角与角终边相同,角与角终边相同,角应与角终边相同,故应选C.
考法04 角度与弧度之间的互化
1.将角度化为弧度
rad;rad;rad.
2.将弧度化为角度
;;.
3.需记住的特殊角的度数与弧度数的对应值
度
弧度 0
【说明】(1)以弧度为单位表示角时,“弧度”两字可以省略不写.如是指sin(2弧度);是指弧度.以度为单位表示角时,度就不能省去.
(2)以弧度为单位表示角时,常常把弧度数写成多少的形式,如无特殊要求,不必把化成小数,如弧度,不必写成弧度.
(3)弧度制和角度制一样,都是一种度量角的单位制.弧度制与角度制相比有一定的优点,其一体现在进位上,角度制在度、分、秒上是六十进制,不便于计算,而弧度制是十进制,给运算带来了方便;其二体现在弧长公式与扇形面积公式的表达上,弧度制下的公式比角度制下的公式简单,运用起来更方便.
(4)用角度制和弧度制来度量零角,虽然单位不同,但数量相同,对于其他非零角,由于单位不同,数量也就不同了.
(5)在进行角度与弧度的换算时,抓住关系式rad是关键,由它可以得到:角度弧度,弧度角度.
1.将下列角度与弧度进行互化:
(1);(2);(3);(4).
【思路分析】利用公式1°= rad或1 rad=进行换算.
【解析】(1);
(2);
(3);
(4).
【跟踪训练】(1)化为弧度是( )
A. B. C. D.
(2)化为角度是( )
A. B. C. D.
【思路分析】利用公式1°= rad或1 rad=进行换算.
【答案】B C
【解析】(1)∵rad,
∴.故选B.
(2)∵1 rad,
∴ rad,故选C.
考法05 弧长与面积公式
1.弧长公式
在半径为的圆中,弧长为的弧所对的圆心角大小为,则,变形可得,此公式称为弧长公式,其中的是弧度角.
2.扇形面积公式
因为圆心角为1 rad的扇形面积为,而弧长为l的扇形的圆心角大小为rad,所以其面积为,将代入上式可得,此公式称为扇形面积公式.
3.弧长公式及扇形面积公式的两种表示
角度制 弧度制
弧长公式
扇形面积公式
注意事项 是扇形的半径,是圆心角的角度数 是扇形的半径,是圆心角的弧度数,是弧长
显然弧度制下的两个公式在形式上都要简单的多,记忆和应用也就更加方便.
已知一个扇形的周长为,圆心角为,求这个扇形的面积.
【思路分析】先根据扇形的周长等于弧长加两个半径长列出方程,求出半径的长度,再用扇形的面积公式计算.
【解析】设扇形的半径为,面积为,
则扇形的圆心角为.
∴扇形的弧长为,
∴,
∴.
∴.
即扇形的面积为.
【解题技巧】求扇形面积的关键是求得扇形的圆心角、半径、弧长三个量中的任意两个量.相反,也可由扇形的面积结合其他条件,求扇形的圆心角、半径、弧长.解题时要注意公式的灵活变形及方程思想的运用.
【跟踪训练】直径为20 cm的圆中,求弧度为的圆心角所对的弧长及该扇形的面积.
【思路分析】先用弧长公式求出弧长,再用扇形的面积公式求出扇形的面积.
【解析】因为直径为20 cm,
所以cm,
又,
所以弧长(cm),
面积().
题组A 基础过关练
1.已知扇形的弧长为,圆心角为,则该扇形的面积为( )
A. B. C. D.
【答案】B
【解析】扇形的圆心角为,弧长为,
扇形的半径,
扇形的面积.
故选:B.
2.“数摺聚清风,一捻生秋意”是宋朝朱翌描写折扇的诗句,折扇出人怀袖,扇面书画,扇骨雕琢,是文人雅士的宠物,所以又有“怀袖雅物”的别号.如图是折扇的示意图,其中OA=20cm,∠AOB=120°,M为OA的中点,则扇面(图中扇环)部分的面积是( )
A.cm2 B.cm2 C.cm2 D.cm2
【答案】B
【解析】扇环的面积为.
故选:B
3.与终边相同的角是( )
A. B.170° C.20° D.340°
【答案】D
【解析】与终边相同的角一定可以写成的形式,,
令 可得,与终边相同,其它选项均不合题意,故选:.
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A.120° B.135° C.150° D.165°
【答案】C
【解析】一日十二个时辰,则一个时辰所对应的圆心角为,丑时与午时相差个时辰,故丑时与午时的夹角为
故选:C
5.装饰公司制作一种扇形板状装饰品,其圆心角为,并在扇形弧上正面等距安装7个发彩光的小灯泡且在背面用导线将小灯泡串连(弧的两端各一个灯泡,导线接头忽略不计),已知扇形的半径为30厘米,则连接导线大致需要的长度约为( )
A.55厘米 B.63厘米 C.69厘米 D.76厘米
【答案】B
【解析】因为在弧长比较短的情况下分成6等份,每部分的弦长和弧长相差很小,
所以可以用弧长近似代替弦长,
所以导线的长度为(厘米).故选:B
6.密位制是度量角的一种方法.把一周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位的单位制叫做密位制.在角的密位制中,采用4个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数和十位数之间画一条短线连接(不足100密位的角用0补全百位和十位),例如7密位写成“”,2021密位写成“”,1周角等于6000密位,记作“”.如果一个半径为2的扇形的面积为,则其圆心角用密位制表示为( )
A. B. C. D.
【答案】B
【解析】设扇形半径为r,圆心角为,则扇形面积为,
则,则其表示的密位为,即17-50.故选:B
7.密位制是度量角的一种方法.将周角等分为6000份,每一份叫做1密位的角.以密位作为角的度量单位,这种度量角的单位制,叫做角的密位制.在角的密位制中,采用四个数码表示角的大小,单位名称密位二字可以省去不写.密位的写法是在百位数字与十位数字之间画一条短线,如:478密位写成“4-78”,1周角等于6000密位,记作1周角.如果一个扇形的半径为2,面积为,则其圆心角可以用密位制表示为( )
A.25-00 B.35-00 C.42-00 D.70-00
【答案】B
【解析】设扇形的圆心角为,则,则,
由题意可知,其密位大小为密位,用密位制表示为35-00.故选:B.
8.刘徽是中国魏晋时期杰出的数学家,他提出“割圆求周”方法:当n很大时,用圆内接正边形的周长近似等于圆周长,并计算出精确度很高的圆周率.在《九章算术注》中总结出“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”的极限思想.运用此思想,当取时,可得的近似值为( )
A. B. C. D.
【答案】D
【解析】将一个单位圆分成个扇形,则每个扇形的圆心角度数均为
由圆的垂径定理,可得每个圆心角所对的弦长,
因为这个扇形对应的弦长之和近似于单位圆的周长,
所以,
所以.
故选:D.
题组B 能力提升练
1.中国传统折扇文化有着极其深厚的底蕴,一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形(如图)的面积为,圆心角为,圆面中剩余部分的面积为,圆心角为,当与的比值为(黄金分割比)时,折扇看上去较为美观,那么( )
A. B. C. D.
【答案】BCD
【解析】设扇形的半径为,由,故D正确;
由,
所以,解得,故C正确;
由,则,
所以,
所以,故B正确.故选:BCD
2.下列说法错误的是( )
A.第二象限角比第一象限角大
B.角与角是终边相同角
C.钝角一定是第二象限角
D.将表的分针拨慢10分钟,则分针转过的角的弧度数为
【答案】AB
【解析】A中,第二象限角比第一象限角大不正确,如是第二象限角,是第一象限角;
B中,因为,所以角与角终边不同,故错误;
C中,因为钝角的范围为,所以钝角是第二象限角,故正确;
D中,将表的分针拨慢10分钟,则分针转过的角的弧度数为正确.故选:AB
3.关于角度,下列说法正确的是( )
A.时钟经过两个小时,时针转过的角度是
B.钝角大于锐角
C.三角形的内角必是第一或第二象限角
D.若是第二象限角,则是第一或第三象限角
【答案】BD
【解析】对于A,时钟经过两个小时,时针转过的角是,故错误;
对于B,钝角一定大于锐角,显然正确;
对于C,若三角形的内角为,是终边在轴正半轴上的角,故错误;
对于D,角的终边在第二象限,
,,
,
当为偶数时,,,得是第一象限角;
当为奇数时,,,得是第三象限角,故正确.故选:BD
4.如图,扇形的圆心角为,半径为,记弓形的面积为,扇形的面积为,则______.
【答案】
【解析】扇形的面积,
弓形的面积,
则,
故答案为:.
5.折扇是一种用竹木做扇骨,韧纸或绫绢做扇面的能折叠的扇子.用时须展开,成扇形,聚头散尾.如图,某折扇的扇骨长度,扇面长度,已知折扇展开所对圆心角的弧度为,则扇面的面积为___________.
【答案】
【解析】由题可知,扇面的面积为.故答案为:.
6.与终边相同的最小正角是___________.
【答案】
【解析】因为,所以与终边相同的最小正角是.故答案为:.
7.在与角终边相同的角中,求满足下列条件的角.
(1)最小的正角;
(2)最大的负角;
(3)内的角.
【答案】(1);(2);(3)、、、.
【解析】
和终边相同
其余的终边相同的角度可以写成
(1)当时是最小的正角,;
(2)当时是最大的负角,;
(3)当,,0,1时,、、、符合条件.
8.将下列角度化为弧度,弧度转化为角度
(1),(2),(3),(4),(5),(6).
【答案】(1);(2);(3);(4);(5);(6).
【解析】(1)弧度弧度,
(2)弧度弧度,
(3)弧度弧度.
(4)弧度,
(5)弧度,
(6)弧度.
题组C 培优拔尖练
1.若是第二象限的角,则的终边所在位置可能是( )
A.第一象限 B.第二象限
C.第三象限 D.笫四象限
【答案】ABD
【解析】是第二象限的角,则,,
,,
当时,是第一象限角,
当时,是第二象限角,
当时,是第四象限角,故选:ABD.
2.下列命题中正确的是( )
A.若角是第三象限角,则可能在第三象限
B.
C.若且,则为第二象限角
D.锐角终边上一点坐标为,则
【答案】ACD
【解析】对于,角是第三象限角,即,所以,当时, 为第一象限角; 当时, 为第三象限角; 当时, 为第四象限角,故可能在第三象限正确,故选项正确.
对于,运用诱导公式化简,故选项不正确.
对于,若,则为第二象限角或者第四象限角,若,则为第一象限角或者第二象限角,同时满足且,则为第二象限角,故选项正确.
对于,因为锐角终边上一点坐标为,由三角函数定义可得,又因为,所以,故选项正确.综上选项正确.故选
3.在北纬圈上有甲、乙两地,若它们在纬度圈上的弧长等于(为地球半径),则这两地间的球面距离为_______ .
【答案】
【解析】设甲、乙两地分别为,
北纬圈所在圆的半径为,
它们在纬度圈上所对应的劣弧长等于(为地球半径),
(是两地在北纬60圈上对应的圆心角),
故.
所以线段
设地球的中心为,则是等边三角形,
所以,
故这两地的球面距离是.
4.如图,已知长为,宽为的长方形在桌面上作无滑动翻滚,翻滚到第四次时被小木块挡住,此时长方形的底边与桌面所成的角为,求点走过的路程及走过的弧所在扇形的总面积.
【答案】, .
【解析】如图:
在扇形中,圆心角为,
弧长,
面积.
在扇形中,圆心角为,
弧长,
面积,
在扇形中,圆心角为,
弧长,
面积.
综上,点走过的路程,
点走过的弧所在扇形的总面积.
5.一只红蚂蚁与一只黑蚂蚁在一个圆(半径为的圆)的圆周上爬动,且两只蚂蚁均从点同时逆时针匀速爬动,红蚂蚁每秒爬过角,黑蚂蚁每秒爬过角(其中).如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限.
(1)求,的值.
(2)两只蚂蚁的爬行速度保持不变,若红蚂蚁从点A逆时针匀速爬行,黑蚂蚁同时从点A顺时针匀速爬行,求当它们从点A出发后第一次相遇时,红蚂蚁爬过的距离.
【答案】(1),;(2).
【解析】(1)由题意可得,与都是的整数倍,
不妨设,,
则,,
又两只蚂蚁在第2秒时均位于第二象限,
所以,即,所以,
因为,所以,所以,,
即,;
(2)两只蚂蚁的爬行速度保持不变,若红蚂蚁从点A逆时针匀速爬行,黑蚂蚁同时从点A顺时针匀速爬行,设它们从点A出发后第一次相遇时,所用的时间为秒,
则,即,解得,
所以红蚂蚁爬过的角度为,
因为圆的半径为,
所以红蚂蚁爬过的距离为.
6.已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=10 cm,求扇形的弧长l;
(2)已知扇形的周长为10 cm,面积是4 cm2,求扇形的圆心角;
(3)若扇形周长为20 cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?
【解析】(1)α=60°=rad,∴l=α·R=×10= (cm).
(2)由题意得解得 (舍去),
故扇形圆心角为.
(3)由已知得,l+2R=20.
所以S=lR= (20-2R)R=10R-R2=-(R-5)2+25,所以当R=5时,S取得最大值25,此时l=10,α=2.
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
例4
例5
分层提分
目标导航
知识精讲
能力拓展
例 1
例 2
例 3
例4
例5
分层提分
2 / 2
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
