广东省汕头 实际问题与一元一次不等式1[下学期]
文档属性
| 名称 | 广东省汕头 实际问题与一元一次不等式1[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 59.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-05-22 22:02:00 | ||
图片预览




文档简介
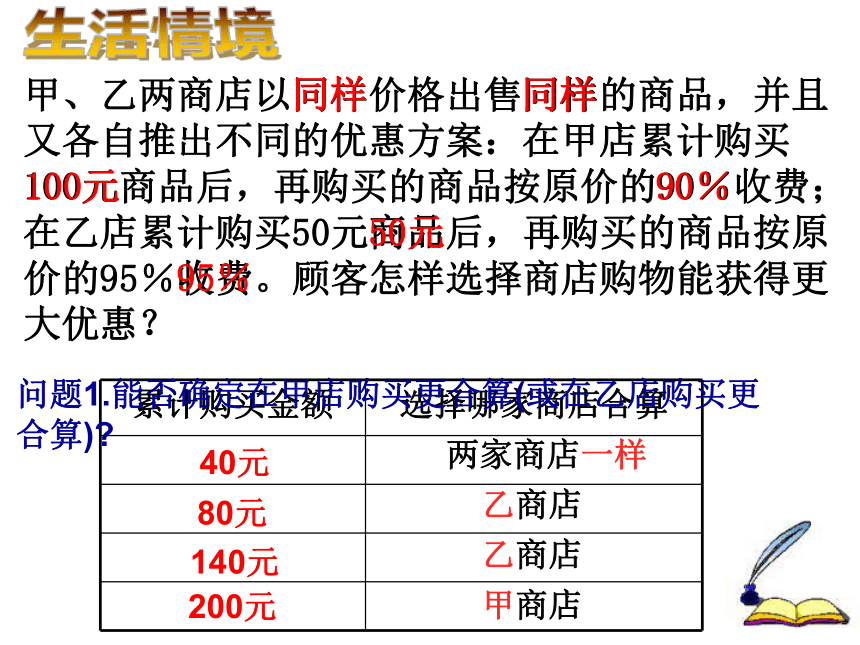
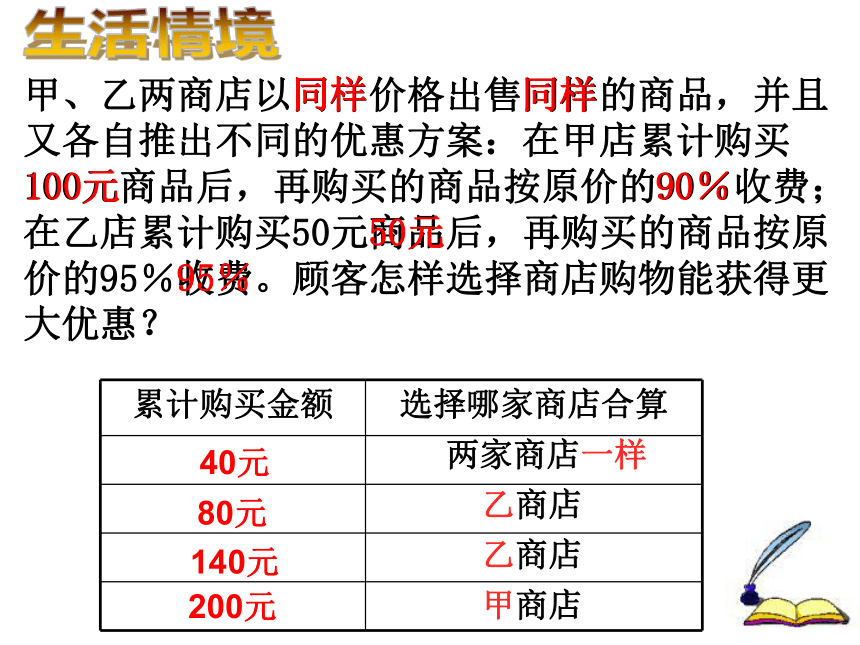
课件13张PPT。数学无处不在实际问题与一元一次不等式(一)本课学习重点:1.解不等式的一般步骤.2.利用不等式建立数学模型解决实际问题.40元两家商店一样乙商店140元200元80元甲商店乙商店甲、乙两商店以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲店累计购买100元商品后,再购买的商品按原价的90%收费;在乙店累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商店购物能获得更大优惠?生活情境同样同样100元50元90%95%问题1.能否确定在甲店购买更合算(或在乙店购买更 合算)?甲、乙两商店以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲店累计购买100元商品后,再购买的商品按原价的90%收费;在乙店累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商店购物能获得更大优惠?生活情境同样同样100元50元90%95%问题2.根据什么标准进行分类?如何分?问题3.当购物款超过100元时,在甲店购物一定更合算吗?40元两家商店一样乙商店140元200元80元甲商店乙商店甲、乙两商店以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲店累计购买100元商品后,再购买的商品按原价的90%收费;在乙店累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商店购物能获得更大优惠?生活情境同样同样100元50元90%95%甲、乙两商店以同样价格出售同样的商品,并且又各自推出不同的优惠方案:在甲店累计购买100元商品后,再购买的商品按原价的90%收费;在乙店累计购买50元商品后,再购买的商品按原价的95%收费。顾客怎样选择商店购物能获得更大优惠?生活情境同样同样100元50元90%95%问题2.根据什么标准进行分类?如何分?问题3.当购物款超过100元时,在甲店购物一定更合算吗?问题4.当购物款超过100元时,建立怎样的数学模型来解决问题?设购物款为x元(x>100元)。 (1)如果在甲商店花费小,则去括号,得:移项,得:合并,得:系数化为1,得:问题5.顾客怎样选择商店购物能获得更大优惠?(2)如果在乙商店花费小,则>(3)如果在两店花费一样,则=答:(1)当购物款不超过50元时,在两店花费一样;(2)当购物款超过50元而不超过100元时,在乙店购物合算;(3)当购物款超过100元而不足150元时,在乙店购物合算;(4)当购物款恰好为150元时,在两店花费一样;(5)当购物款超过150元时,在甲店购物合算.我来小结1.比较解不等式和解方程的步骤,它们有何区别?一元一次不等式的解法和一元一次方程类似,只是系数化为1时,要注意不等号的方向.2.用不等式建立数学模型解决实际问题的一般步骤是怎样的?①审②设③找④列⑤解⑥答当堂训练解下列不等式.生活在线 班主任为了表彰在量化评比中取得优异成绩的同学,带了37元钱去购买笔记本和钢笔共11件.已知钢笔每支5元,笔记本每本3元,问:他最多能买几支钢笔?变式: 班主任共有几种不同的购买方案?实际问题建立数学模型
(一元一次不等式)审题、设未知数根据不等关系列出不等式数学问题的解实际问题的解检验解一元一次不等式回顾反思体验中考(05·河南)某公司为了扩大经营,决定购进6台机器用于生产某种活塞,现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示,经过预算,本次购买机器所耗资金不能超过34万元.(1)按该公司要求可以有几种购买方案?(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种方案?
(一元一次不等式)审题、设未知数根据不等关系列出不等式数学问题的解实际问题的解检验解一元一次不等式回顾反思体验中考(05·河南)某公司为了扩大经营,决定购进6台机器用于生产某种活塞,现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示,经过预算,本次购买机器所耗资金不能超过34万元.(1)按该公司要求可以有几种购买方案?(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种方案?
