人教A版(2019)高中数学必修第一册5-1-1任意角作业(含答案)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册5-1-1任意角作业(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 317.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-18 07:18:39 | ||
图片预览



文档简介
课时作业(三十五) 任意角
一、选择题
1.终边为第一象限和第三象限的平分线的角的集合是( )
A.{α|α=45°+k·360°,k∈Z}
B.{α|α=-135°+k·180°,k∈Z}
C.{α|α=-135°+k·360°,k∈Z}
D.{α|α=135°+k·180°,k∈Z}
2.若角α满足α=45°+k·180°,k∈Z,则角α的终边落在( )
A.第一象限或第三象限
B.第一象限或第二象限
C.第二象限或第四象限
D.第三象限或第四象限
3.若α是第四象限角,则180°+α是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A. 120° B. 135° C. 150° D. 165°
5.已知角2α的终边在x轴的上方,那么α是( )
A.第一象限角
B.第一象限角或第二象限角
C.第一象限角或第三象限角
D.第一象限角或第四象限角
6.集合M=,P=eq \b\lc\{\rc\}(\a\vs4\al\co1(x\b\lc\|\rc\ (\a\vs4\al\co1(x=±90°,k∈Z)))) ,则M,P之间的关系为( )
A.M=P B.M P
C.M P D.M∩P=
二、填空题
7.在0°~360°范围内:与-1 000°终边相同的最小正角是________,是第________象限角.
8.角α,β的终边关于y轴对称,若α=30°,则β=________.
9.(2022·哈尔滨调考)如图,点A在半径为1且圆心在原点的圆上,且∠AOx=45°,点P从点A处出发,按逆时针方向沿单位圆匀速旋转.已知点P在1 s内转过的角度为θ(0°<θ<180°),经过2 s第一次到达第三象限,经过14 s又回到出发点A,则θ=________.
三、解答题
10.已知角x的终边落在图示阴影部分区域(包括边界),写出角x组成的集合.
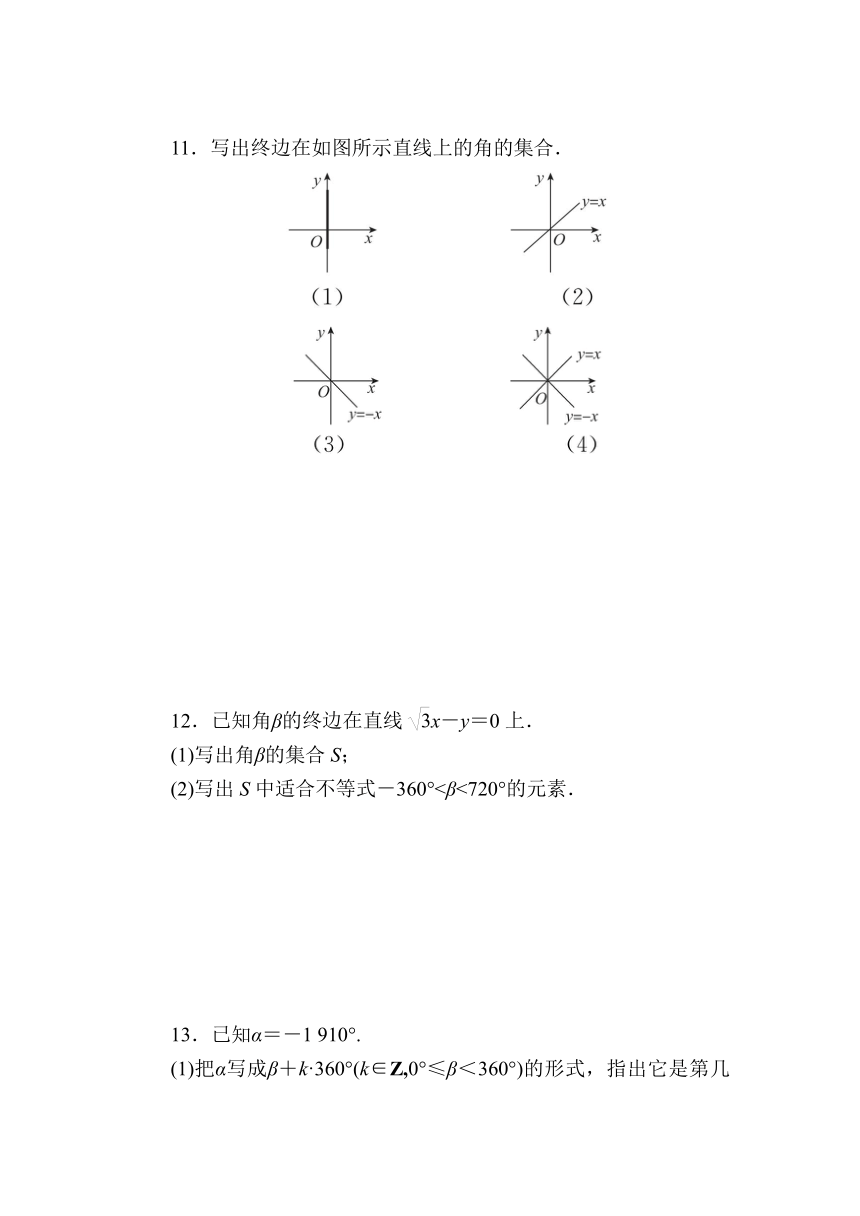
11.写出终边在如图所示直线上的角的集合.
12.已知角β的终边在直线x-y=0上.
(1)写出角β的集合S;
(2)写出S中适合不等式-360°<β<720°的元素.
13.已知α=-1 910°.
(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,指出它是第几象限角;
(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.
课时作业(三十五) 任意角
一、选择题
1.终边为第一象限和第三象限的平分线的角的集合是( )
A.{α|α=45°+k·360°,k∈Z}
B.{α|α=-135°+k·180°,k∈Z}
C.{α|α=-135°+k·360°,k∈Z}
D.{α|α=135°+k·180°,k∈Z}
答案:B
解析:终边为第一象限的平分线的角的集合是{α|α=45°+k·360°,k∈Z}①,终边为第三象限的平分线的角的集合是{α|α=-135°+k·360°,k∈Z}②,由①②得{α|α=-135°+k·180°,k∈Z},故选B.
2.若角α满足α=45°+k·180°,k∈Z,则角α的终边落在( )
A.第一象限或第三象限
B.第一象限或第二象限
C.第二象限或第四象限
D.第三象限或第四象限
答案:A
3.若α是第四象限角,则180°+α是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
答案:B
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A. 120° B. 135° C. 150° D. 165°
答案:C
解析:一日十二个时辰,则一个时辰所对应的圆心角为=30°,丑时与午时相差5个时辰,故丑时与午时的夹角为30°×5=150°,故选C.
5.已知角2α的终边在x轴的上方,那么α是( )
A.第一象限角
B.第一象限角或第二象限角
C.第一象限角或第三象限角
D.第一象限角或第四象限角
答案:C
6.集合M=,P=eq \b\lc\{\rc\}(\a\vs4\al\co1(x\b\lc\|\rc\ (\a\vs4\al\co1(x=±90°,k∈Z)))) ,则M,P之间的关系为( )
A.M=P B.M P
C.M P D.M∩P=
答案:B
二、填空题
7.在0°~360°范围内:与-1 000°终边相同的最小正角是________,是第________象限角.
答案:80° 一
解析:-1 000°=-3×360°+80°,∴与-1 000°终边相同的最小正角是80°,是第一象限角.
8.角α,β的终边关于y轴对称,若α=30°,则β=________.
答案:150°+k·360°,k∈Z
9.(2022·哈尔滨调考)如图,点A在半径为1且圆心在原点的圆上,且∠AOx=45°,点P从点A处出发,按逆时针方向沿单位圆匀速旋转.已知点P在1 s内转过的角度为θ(0°<θ<180°),经过2 s第一次到达第三象限,经过14 s又回到出发点A,则θ=________.
答案:或
解析:由题意,得14θ+45°=n·360°+45°(n∈Z),所以θ=(n∈Z).又因为180°<2θ+45°<270°,即67.5°<θ<112.5°,所以n=3或n=4,所以θ=或θ=.
三、解答题
10.已知角x的终边落在图示阴影部分区域(包括边界),写出角x组成的集合.
解:(1){x|k·360°-135°≤x≤k·360°+135°,k∈Z}.
(2){x|k·360°+30°≤x≤k·360°+60°,k∈Z}∪{x|k·360°+210°≤x≤k·360°+240°,k∈Z}={x|k·180°+30°≤x≤k·180°+60°,k∈Z}.
11.写出终边在如图所示直线上的角的集合.
解:(1)S={α|α=90°+k·180°,k∈Z}.
(2)S={α|α=45°+k·180°,k∈Z}.
(3)S={α|α=135°+k·180°,k∈Z}.
(4)S={α|α=45°+k·180°,k∈Z}∪{α|α=135°+k·180°,k∈Z}={α|α=45°+2k·90°,k∈Z}∪{α|α=45°+(2k+1)·90°,k∈Z}={α|α=45°+n·90°,n∈Z}.
12.已知角β的终边在直线x-y=0上.
(1)写出角β的集合S;
(2)写出S中适合不等式-360°<β<720°的元素.
解:(1)如图,直线x-y=0过原点,倾斜角为60°,在0°~360°范围内,终边落在射线OA上的角是60°,终边落在射线OB上的角是240°,所以以射线OA,OB为终边的角的集合为:
S1={β|β=60°+k·360°,k∈Z},
S2={β|β=240°+k·360°,k∈Z},
所以角β的集合S=S1∪S2={β|β=60°+k·360°,k∈Z}∪{β|β=60°+180°+k·360°,k∈Z}={β|β=60°+2k·180°,k∈Z}∪{β|β=60°+(2k+1)·180°,k∈Z}={β|β=60°+n·180°,n∈Z}.
(2)由于-360°<β<720°,即-360°<60°+n·180°<720°,n∈Z,解得-所以n=-2,-1,0,1,2,3.
所以S中适合不等式-360°<β<720°的元素为:
60°-2×180°=-300°;
60°-1×180°=-120°;
60°+0×180°=60°;
60°+1×180°=240°;
60°+2×180°=420°;
60°+3×180°=600°.
13.已知α=-1 910°.
(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,指出它是第几象限角;
(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.
解:(1)设α=β+k·360°(k∈Z),则β=-1 910°-k·360°(k∈Z).令0°≤-1 910°-k·360°<360°,解得-6(2)令θ=250°+n·360°(n∈Z),取n=-1,-2就得到符合-720°≤θ<0°的角.250°-360°=-110°,250°-720°=-470°.故θ=-110°或-470°.
一、选择题
1.终边为第一象限和第三象限的平分线的角的集合是( )
A.{α|α=45°+k·360°,k∈Z}
B.{α|α=-135°+k·180°,k∈Z}
C.{α|α=-135°+k·360°,k∈Z}
D.{α|α=135°+k·180°,k∈Z}
2.若角α满足α=45°+k·180°,k∈Z,则角α的终边落在( )
A.第一象限或第三象限
B.第一象限或第二象限
C.第二象限或第四象限
D.第三象限或第四象限
3.若α是第四象限角,则180°+α是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A. 120° B. 135° C. 150° D. 165°
5.已知角2α的终边在x轴的上方,那么α是( )
A.第一象限角
B.第一象限角或第二象限角
C.第一象限角或第三象限角
D.第一象限角或第四象限角
6.集合M=,P=eq \b\lc\{\rc\}(\a\vs4\al\co1(x\b\lc\|\rc\ (\a\vs4\al\co1(x=±90°,k∈Z)))) ,则M,P之间的关系为( )
A.M=P B.M P
C.M P D.M∩P=
二、填空题
7.在0°~360°范围内:与-1 000°终边相同的最小正角是________,是第________象限角.
8.角α,β的终边关于y轴对称,若α=30°,则β=________.
9.(2022·哈尔滨调考)如图,点A在半径为1且圆心在原点的圆上,且∠AOx=45°,点P从点A处出发,按逆时针方向沿单位圆匀速旋转.已知点P在1 s内转过的角度为θ(0°<θ<180°),经过2 s第一次到达第三象限,经过14 s又回到出发点A,则θ=________.
三、解答题
10.已知角x的终边落在图示阴影部分区域(包括边界),写出角x组成的集合.
11.写出终边在如图所示直线上的角的集合.
12.已知角β的终边在直线x-y=0上.
(1)写出角β的集合S;
(2)写出S中适合不等式-360°<β<720°的元素.
13.已知α=-1 910°.
(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,指出它是第几象限角;
(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.
课时作业(三十五) 任意角
一、选择题
1.终边为第一象限和第三象限的平分线的角的集合是( )
A.{α|α=45°+k·360°,k∈Z}
B.{α|α=-135°+k·180°,k∈Z}
C.{α|α=-135°+k·360°,k∈Z}
D.{α|α=135°+k·180°,k∈Z}
答案:B
解析:终边为第一象限的平分线的角的集合是{α|α=45°+k·360°,k∈Z}①,终边为第三象限的平分线的角的集合是{α|α=-135°+k·360°,k∈Z}②,由①②得{α|α=-135°+k·180°,k∈Z},故选B.
2.若角α满足α=45°+k·180°,k∈Z,则角α的终边落在( )
A.第一象限或第三象限
B.第一象限或第二象限
C.第二象限或第四象限
D.第三象限或第四象限
答案:A
3.若α是第四象限角,则180°+α是( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
答案:B
4.如图是清代的时辰醒钟,此醒钟直径12.5厘米,厚7.5厘米,由清朝宫廷钟表处制造,以中国传统的一日十二个时辰为表盘显示,其内部结构与普通机械钟表的内部结构相似.则丑时与午时的夹角是( )
A. 120° B. 135° C. 150° D. 165°
答案:C
解析:一日十二个时辰,则一个时辰所对应的圆心角为=30°,丑时与午时相差5个时辰,故丑时与午时的夹角为30°×5=150°,故选C.
5.已知角2α的终边在x轴的上方,那么α是( )
A.第一象限角
B.第一象限角或第二象限角
C.第一象限角或第三象限角
D.第一象限角或第四象限角
答案:C
6.集合M=,P=eq \b\lc\{\rc\}(\a\vs4\al\co1(x\b\lc\|\rc\ (\a\vs4\al\co1(x=±90°,k∈Z)))) ,则M,P之间的关系为( )
A.M=P B.M P
C.M P D.M∩P=
答案:B
二、填空题
7.在0°~360°范围内:与-1 000°终边相同的最小正角是________,是第________象限角.
答案:80° 一
解析:-1 000°=-3×360°+80°,∴与-1 000°终边相同的最小正角是80°,是第一象限角.
8.角α,β的终边关于y轴对称,若α=30°,则β=________.
答案:150°+k·360°,k∈Z
9.(2022·哈尔滨调考)如图,点A在半径为1且圆心在原点的圆上,且∠AOx=45°,点P从点A处出发,按逆时针方向沿单位圆匀速旋转.已知点P在1 s内转过的角度为θ(0°<θ<180°),经过2 s第一次到达第三象限,经过14 s又回到出发点A,则θ=________.
答案:或
解析:由题意,得14θ+45°=n·360°+45°(n∈Z),所以θ=(n∈Z).又因为180°<2θ+45°<270°,即67.5°<θ<112.5°,所以n=3或n=4,所以θ=或θ=.
三、解答题
10.已知角x的终边落在图示阴影部分区域(包括边界),写出角x组成的集合.
解:(1){x|k·360°-135°≤x≤k·360°+135°,k∈Z}.
(2){x|k·360°+30°≤x≤k·360°+60°,k∈Z}∪{x|k·360°+210°≤x≤k·360°+240°,k∈Z}={x|k·180°+30°≤x≤k·180°+60°,k∈Z}.
11.写出终边在如图所示直线上的角的集合.
解:(1)S={α|α=90°+k·180°,k∈Z}.
(2)S={α|α=45°+k·180°,k∈Z}.
(3)S={α|α=135°+k·180°,k∈Z}.
(4)S={α|α=45°+k·180°,k∈Z}∪{α|α=135°+k·180°,k∈Z}={α|α=45°+2k·90°,k∈Z}∪{α|α=45°+(2k+1)·90°,k∈Z}={α|α=45°+n·90°,n∈Z}.
12.已知角β的终边在直线x-y=0上.
(1)写出角β的集合S;
(2)写出S中适合不等式-360°<β<720°的元素.
解:(1)如图,直线x-y=0过原点,倾斜角为60°,在0°~360°范围内,终边落在射线OA上的角是60°,终边落在射线OB上的角是240°,所以以射线OA,OB为终边的角的集合为:
S1={β|β=60°+k·360°,k∈Z},
S2={β|β=240°+k·360°,k∈Z},
所以角β的集合S=S1∪S2={β|β=60°+k·360°,k∈Z}∪{β|β=60°+180°+k·360°,k∈Z}={β|β=60°+2k·180°,k∈Z}∪{β|β=60°+(2k+1)·180°,k∈Z}={β|β=60°+n·180°,n∈Z}.
(2)由于-360°<β<720°,即-360°<60°+n·180°<720°,n∈Z,解得-
所以S中适合不等式-360°<β<720°的元素为:
60°-2×180°=-300°;
60°-1×180°=-120°;
60°+0×180°=60°;
60°+1×180°=240°;
60°+2×180°=420°;
60°+3×180°=600°.
13.已知α=-1 910°.
(1)把α写成β+k·360°(k∈Z,0°≤β<360°)的形式,指出它是第几象限角;
(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.
解:(1)设α=β+k·360°(k∈Z),则β=-1 910°-k·360°(k∈Z).令0°≤-1 910°-k·360°<360°,解得-6
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
