八年级数学北师大版上册 6.3 从统计图分析数据的集中趋势 教案(表格式)
文档属性
| 名称 | 八年级数学北师大版上册 6.3 从统计图分析数据的集中趋势 教案(表格式) |  | |
| 格式 | zip | ||
| 文件大小 | 325.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-17 20:13:35 | ||
图片预览




文档简介
教学设计
从统计图分析数据的集中趋势
课题名称 6.3从统计图分析数据的集中趋势
科 目 数学 年 级 BS八年级上
授课类型 新授课
教学时间 40分钟
教材分析 信息时代背景下,海量图片、表格、数据与人们的生活息息相关,但很多时候无法获取原始数据,更多情况下我们面对的是统计图和统计表,于是能否对图表所示的信息做出准确解读成为人们的基本素养。因此初中阶段的主要目标则是带领学生经历完整的统计过程,学会分析数据,学会用数据说话,树立统计意识。 《义务教育阶段数学课程标准(2011年版)》指出,经过统计的学习,学生能学会用统计图描述数据,知道对于同样的数据有可以有多种分析方法,数据分析是统计的核心。 在此前学生已学会了用折线统计图、条形统计图、扇形统计图等来描述数据,会用平均数、中位数和众数分析一组数据的集中趋势,这是本堂课学习的知识基础。但本堂课也不是对先前知识内容的简单复习,而是学会从统计图中获取信息,而如何从统计图中观察出一组数据的平均数、中位数和众数?如何不经过计算对数据的集中趋势做出合理估计?这就是本节课要解决的问题。
学情分析 学生已经掌握了条形统计图、扇形统计图等统计图的画法,并能从其中获取一些简单的信息描述数据,此外在上两节课的学习中,学生学会了如何求一组数据的平均数、中位数和众数,知道运用这些统计量可以描述一组数据的集中趋势。
教学目标 知识与技能目标:能从条形统计图、扇形统计图等统计图中获取信息,求出或估计一组数据的平均数、中位数和众数。 过程与方法目标:经过从统计图中分析数据集中趋势的过程,发展几何直观,逐步提高数据分析能力。 情感态度与价值观目标:在用统计图分析数据的过程中感受数据与几何图形间的联系,利用几何图形感受数据集中趋势,发展数形结合的观念。
教学重点 能从条形统计图、扇形统计图等统计图中求出或估计一组数据的平均数、中位数和众数
教学难点 结合统计图的几何特征估计数据的集中趋势
教学方法 探究法、活动法
教学准备 调查问卷、EXCEL表格、白板课件
教学过程 设计意图
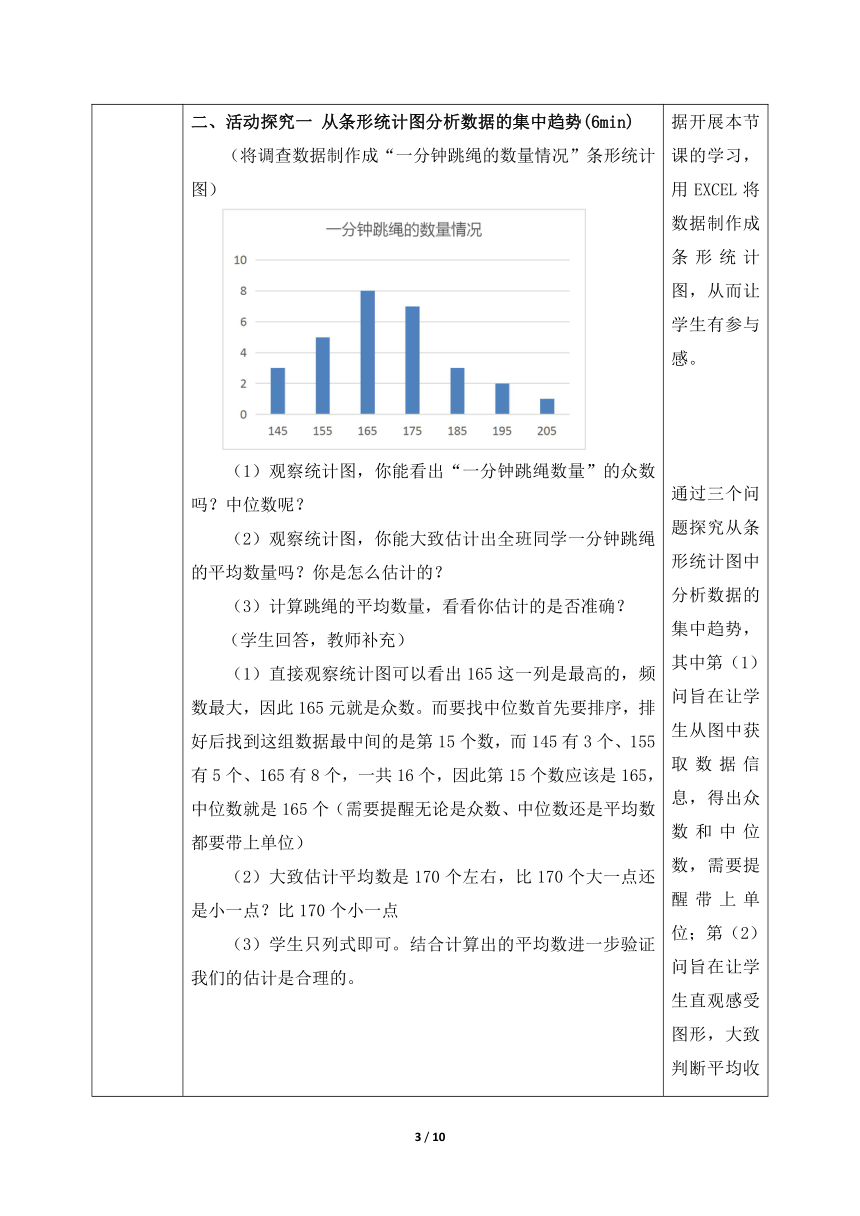
活动导入(5min) 开展“一分钟跳绳情况调查”活动,用EXCEL表格将收集到的数据制作成条形统计图、扇形统计图。 下发一分钟跳绳情况调查表,每组一张,按顺序匿名填写,每人在相应的表格里标记,按画“正”字的方式填表,如第一个人画“一”,第二个人画“|”……由每组最后一位同学告诉老师相应人数。 根据调查数据利用EXCEL绘制条形统计图和扇形统计图。 (在调查的同时回忆学过哪些统计图,数据的集中趋势可以用哪些统计量来描述) 师:为什么要把统计图和数据的集中趋势放到一起呢?在之前我们研究平均数、中位数和众数时都是用数据/数据表来算的,这节课就用统计图分析数据的集中趋势。 活动探究一 从条形统计图分析数据的集中趋势(6min) (将调查数据制作成“一分钟跳绳的数量情况”条形统计图) 观察统计图,你能看出“一分钟跳绳数量”的众数吗?中位数呢? 观察统计图,你能大致估计出全班同学一分钟跳绳的平均数量吗?你是怎么估计的? 计算跳绳的平均数量,看看你估计的是否准确? (学生回答,教师补充) 直接观察统计图可以看出165这一列是最高的,频数最大,因此165元就是众数。而要找中位数首先要排序,排好后找到这组数据最中间的是第15个数,而145有3个、155有5个、165有8个,一共16个,因此第15个数应该是165,中位数就是165个(需要提醒无论是众数、中位数还是平均数都要带上单位) 大致估计平均数是170个左右,比170个大一点还是小一点?比170个小一点 学生只列式即可。结合计算出的平均数进一步验证我们的估计是合理的。 【议一议】 (课本P145议一议) 甲、乙、丙三支青年排球队各有12名运动员,三队队员的年龄情况如图。 (1)观察三幅图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢? (2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的? (3)计算出乙、丙球队队员的平均年龄,看看你估计的是否准确。 (学生回答,教师补充) 条形统计图中柱子最高的就是众数,甲队众数是20岁、乙队的众数是19岁、丙队的众数是21岁。要找中位数就要知道最中间的是第几位,一共十二名队员,所以要找第6、第7名是几岁,以甲队为例,18岁的1个,19岁的3个,这一共是4个数据,20岁的4个,到这是8个数据,所以第6、第7名都是20岁,所以中位数是20岁。所以无论是众数还是中位数,三支队年龄的大小关系都是乙<甲<丙,那平均数是不是也是这个关系?(引出(2)) 先看甲队,甲队的条形图给人的感觉是以20为基准,两边的数据向20集中,而乙队不是,乙队与甲队相比这个图怎么样了?——往左偏,更向左集中一点,所以谁的平均年龄更大些?再看丙,与甲队相比丙这个图往右偏,集中在右边,那么与甲相比,丙队平均年龄更大.(换个角度理解:权重)乙队平均年龄更小,理由是丙队21、22岁的人数较多,一下就把平均年龄拉高了,整体来看丙队的统计图“向右偏移”,乙队18、19岁的人数较多,一下就把平均年龄拉低了,且整体来看乙队的统计图“向左偏移”。 如何看估计的准不准呢?需要计算,先看甲,以20为基准,19就是-1,21就是+1,18就是-2,22就是+2,算甲的平均年龄: (上式让学生板书,强调单位) 因此甲的平均年龄就是20岁 同样的方法来算乙、丙的平均年龄。 通过计算能再次验证我们的估计是合理的,但是计算很麻烦,所以在生活中有时候不需要特别精确的计算,只需要合理估算,所以我们要学会从统计图中做估算,但估算总会有偏差,所以需要计算来验证,从而积累我们估算的经验。 回顾:在条形统计图中怎么找众数?——柱子最高的。怎么找中位数?——首先得知道总数是多少,接着确定最中间的是第几个数再从第一根柱子开始做加法去找。而平均数要麻烦一些,但找一个基准后可以简化运算量。 活动探究二 从扇形统计图分析数据的集中趋势 (将调查数据制作成“一分钟跳绳情况”扇形统计图) (在课件中再重复一下已知条件:全班29个人) 师:刚刚我们知道了用条形统计图如何求出或估计平均数、中位数和众数。下面看看扇形统计图,还是同学们的一分钟跳绳,制作成了扇形统计图。 (1)观察统计图,你能看出“一分钟跳绳数量”的众数吗?中位数呢? (2)全班同学一分钟跳绳的平均数量是多少? (3)如果不知道全班同学总人数,还能求平均数吗? (学生思考,特别是中位数、平均数,教师补充) (给学生时间计算平均数,展示不同计算方法,引出第(3)问) (1)占比最大的数据165个就是众数。那中位数呢?(学生说怎么找)要找中位数首先要排序,这个图里排好了吗?排好了再找最中间,你想整个扇形图是100%,最中间得是百分之多少?50%、51%。那我就从头开始找,一直加到 才够50%,因此中位数就是 。有没有更简单的方法?起始是145这个数,以145为起点,沿着半径把扇形图劈成两半,到这恰好就是50%,这就是中位数。但是这个方法有局限性,能从任意一个位置劈开吗?不行,一定得从排好序的第一个数开始,而且如果这个图不按顺序排,就不能用这个办法了。所以还是第一种办法适用于大多数情况。 (2)(学生可能利用扇形图的百分比算出各项数据对应的人数,之后再计算平均数;也可能不计算出相应人数,直接用各项数据乘以相应百分比)。 (让学生把式子写在黑板上) (一定要对比两种方法!) 其中法一是先把人数算出来,而法二直接乘以的百分比,由于法一中29可以约分,所以两种方法本质上一样,但法二更简单。——追问第(3)问 (3)在法二中并没有用到总人数,也算出了平均数,所以在扇形统计图中不知道总数的情况下仍能计算出平均数。在条形统计图中可以吗?为什么在扇形图中就可以?这些百分比其实就是数据的“权”。看似第二种方法没有除以总数,但实际上是除以了100%。所以可以直接利用各项数据的百分比求平均数。 【议一议】用散点图估计数据的集中趋势 (课本P145) 为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如图所示。 这10个面包质量的众数是多少?中位数是多少? 你能估计出一个这样的面包的平均质量是吗?你是怎么估计的? (1)发现100这条线上的点最多,因此众数是100g;在10个数据中,中位数是第5、第6个数据的平均数,那么就按顺序去数第5、第6个数,因此中位数就是100g。 (2)平均数怎么算? 法一:公式,都加起来再除以10. 法二:以100g为基准,超过100g记为正数、低于100g记为负数,这样计算起来更简单点。 法三:在条形统计图中估算平均数时用到了如果图形轴对称,那么两边数据可以相互中和,那在散点图中看两边的数据能否“中和”。 两边的数据105与95的平均数是100、103与97的平均数是100、101和99的平均数是100,还剩下一个98,它就会把平均水平拉低,平均质量会低于100g.你能想想会低多少吗?总共低了2g,一个十个数据,平均每一个就低了0.2g,因此它的平均质量就是99.8g。 课堂小结 我们今天学习了如何从统计图分析数据的集中趋势,包括平均数、中位数和众数,最好求的是谁?——众数,条形统计图中最高的、扇形统计图中面积最大的就是众数。其次中位数也比较好求,找准最中间是第几个数就好,无论是众数、中位数还是平均数在实际问题中都要带上单位。比较难算的是平均数,但我们能大概估计平均数的大小,只是估计会有误差,如何提高估计的准确度?在每次估计之后,再算一下,从而积累估计的经验。既然还要算,制作统计图有什么用呢?——图形直观。有时候不需要知道精确的平均水平,只要估计大概即可,这就用到了图形,但估计会有误差,需要计算来验证,这就用到了数。所谓“数形结合”就是这个意思。 最后分享给大家一首诗 数与形,本是相依矣 焉能分作两边飞 数缺形时少直观 形少数时难入微 数形结合百般好 割裂分家万事非 切莫忘,几何代数统一体 永远联系切莫离 ——华罗庚 布置作业 以收集同学们的一分钟跳绳数量的调查活动展开,带领学生经历收集数据、整理数据、分析数据的统计过程,调动学习兴趣。 在活动探究一中,利用收集到的数据开展本节课的学习,用EXCEL将数据制作成条形统计图,从而让学生有参与感。 通过三个问题探究从条形统计图中分析数据的集中趋势,其中第(1)问旨在让学生从图中获取数据信息,得出众数和中位数,需要提醒带上单位;第(2)问旨在让学生直观感受图形,大致判断平均收入的大小;第(3)问则是让学生通过计算验证估计是否合理。 【议一议】的目的在于让学生通过条形统计图的几何特征,再次对数据的集中趋势做出大致判断 在活动探究二中,再将收集到的数据制作成扇形统计图,从中分析数据的集中趋势。 结合上两种统计图的分析经验,用散点统计图分析数据的集中趋势。
板书设计 6.3从统计图分析数据的集中趋势 1.条形统计图 平均数 中位数 2.扇形统计图 众数
教学反思 在第一个【议一议】中应当先讲甲队,再讲乙、丙,把乙、丙看成是甲队向左、向右偏移后的。此外,【议一议】部分讲太久了,估计要10min 计算平均数时可以用找基准点的办法简化运算量。 各个环节的时间控制不到位!出现拖堂现象,要严格把握时间,怕讲不完可以设置超链接,直接链接到小结。(绝不能拖堂!) 声音要在大!强调重点时要有突出! 先写课题!!不要在引入后再写!主板不要写草稿! 要有过渡语!在之前我们研究平均数、中位数和众数时都是用数据/数据表来算的,这节课就用统计图分析数据的集中趋势。 检验学生是否掌握时,要让学生举手回答问题,如果大部分学生举手,说明基本都能掌握。 学生试错、出现回答错误可以作为一个亮点,出现错误之后要让其他同学来评价。
1 / 10
从统计图分析数据的集中趋势
课题名称 6.3从统计图分析数据的集中趋势
科 目 数学 年 级 BS八年级上
授课类型 新授课
教学时间 40分钟
教材分析 信息时代背景下,海量图片、表格、数据与人们的生活息息相关,但很多时候无法获取原始数据,更多情况下我们面对的是统计图和统计表,于是能否对图表所示的信息做出准确解读成为人们的基本素养。因此初中阶段的主要目标则是带领学生经历完整的统计过程,学会分析数据,学会用数据说话,树立统计意识。 《义务教育阶段数学课程标准(2011年版)》指出,经过统计的学习,学生能学会用统计图描述数据,知道对于同样的数据有可以有多种分析方法,数据分析是统计的核心。 在此前学生已学会了用折线统计图、条形统计图、扇形统计图等来描述数据,会用平均数、中位数和众数分析一组数据的集中趋势,这是本堂课学习的知识基础。但本堂课也不是对先前知识内容的简单复习,而是学会从统计图中获取信息,而如何从统计图中观察出一组数据的平均数、中位数和众数?如何不经过计算对数据的集中趋势做出合理估计?这就是本节课要解决的问题。
学情分析 学生已经掌握了条形统计图、扇形统计图等统计图的画法,并能从其中获取一些简单的信息描述数据,此外在上两节课的学习中,学生学会了如何求一组数据的平均数、中位数和众数,知道运用这些统计量可以描述一组数据的集中趋势。
教学目标 知识与技能目标:能从条形统计图、扇形统计图等统计图中获取信息,求出或估计一组数据的平均数、中位数和众数。 过程与方法目标:经过从统计图中分析数据集中趋势的过程,发展几何直观,逐步提高数据分析能力。 情感态度与价值观目标:在用统计图分析数据的过程中感受数据与几何图形间的联系,利用几何图形感受数据集中趋势,发展数形结合的观念。
教学重点 能从条形统计图、扇形统计图等统计图中求出或估计一组数据的平均数、中位数和众数
教学难点 结合统计图的几何特征估计数据的集中趋势
教学方法 探究法、活动法
教学准备 调查问卷、EXCEL表格、白板课件
教学过程 设计意图
活动导入(5min) 开展“一分钟跳绳情况调查”活动,用EXCEL表格将收集到的数据制作成条形统计图、扇形统计图。 下发一分钟跳绳情况调查表,每组一张,按顺序匿名填写,每人在相应的表格里标记,按画“正”字的方式填表,如第一个人画“一”,第二个人画“|”……由每组最后一位同学告诉老师相应人数。 根据调查数据利用EXCEL绘制条形统计图和扇形统计图。 (在调查的同时回忆学过哪些统计图,数据的集中趋势可以用哪些统计量来描述) 师:为什么要把统计图和数据的集中趋势放到一起呢?在之前我们研究平均数、中位数和众数时都是用数据/数据表来算的,这节课就用统计图分析数据的集中趋势。 活动探究一 从条形统计图分析数据的集中趋势(6min) (将调查数据制作成“一分钟跳绳的数量情况”条形统计图) 观察统计图,你能看出“一分钟跳绳数量”的众数吗?中位数呢? 观察统计图,你能大致估计出全班同学一分钟跳绳的平均数量吗?你是怎么估计的? 计算跳绳的平均数量,看看你估计的是否准确? (学生回答,教师补充) 直接观察统计图可以看出165这一列是最高的,频数最大,因此165元就是众数。而要找中位数首先要排序,排好后找到这组数据最中间的是第15个数,而145有3个、155有5个、165有8个,一共16个,因此第15个数应该是165,中位数就是165个(需要提醒无论是众数、中位数还是平均数都要带上单位) 大致估计平均数是170个左右,比170个大一点还是小一点?比170个小一点 学生只列式即可。结合计算出的平均数进一步验证我们的估计是合理的。 【议一议】 (课本P145议一议) 甲、乙、丙三支青年排球队各有12名运动员,三队队员的年龄情况如图。 (1)观察三幅图,你能从图中分别看出三支球队队员年龄的众数吗?中位数呢? (2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的? (3)计算出乙、丙球队队员的平均年龄,看看你估计的是否准确。 (学生回答,教师补充) 条形统计图中柱子最高的就是众数,甲队众数是20岁、乙队的众数是19岁、丙队的众数是21岁。要找中位数就要知道最中间的是第几位,一共十二名队员,所以要找第6、第7名是几岁,以甲队为例,18岁的1个,19岁的3个,这一共是4个数据,20岁的4个,到这是8个数据,所以第6、第7名都是20岁,所以中位数是20岁。所以无论是众数还是中位数,三支队年龄的大小关系都是乙<甲<丙,那平均数是不是也是这个关系?(引出(2)) 先看甲队,甲队的条形图给人的感觉是以20为基准,两边的数据向20集中,而乙队不是,乙队与甲队相比这个图怎么样了?——往左偏,更向左集中一点,所以谁的平均年龄更大些?再看丙,与甲队相比丙这个图往右偏,集中在右边,那么与甲相比,丙队平均年龄更大.(换个角度理解:权重)乙队平均年龄更小,理由是丙队21、22岁的人数较多,一下就把平均年龄拉高了,整体来看丙队的统计图“向右偏移”,乙队18、19岁的人数较多,一下就把平均年龄拉低了,且整体来看乙队的统计图“向左偏移”。 如何看估计的准不准呢?需要计算,先看甲,以20为基准,19就是-1,21就是+1,18就是-2,22就是+2,算甲的平均年龄: (上式让学生板书,强调单位) 因此甲的平均年龄就是20岁 同样的方法来算乙、丙的平均年龄。 通过计算能再次验证我们的估计是合理的,但是计算很麻烦,所以在生活中有时候不需要特别精确的计算,只需要合理估算,所以我们要学会从统计图中做估算,但估算总会有偏差,所以需要计算来验证,从而积累我们估算的经验。 回顾:在条形统计图中怎么找众数?——柱子最高的。怎么找中位数?——首先得知道总数是多少,接着确定最中间的是第几个数再从第一根柱子开始做加法去找。而平均数要麻烦一些,但找一个基准后可以简化运算量。 活动探究二 从扇形统计图分析数据的集中趋势 (将调查数据制作成“一分钟跳绳情况”扇形统计图) (在课件中再重复一下已知条件:全班29个人) 师:刚刚我们知道了用条形统计图如何求出或估计平均数、中位数和众数。下面看看扇形统计图,还是同学们的一分钟跳绳,制作成了扇形统计图。 (1)观察统计图,你能看出“一分钟跳绳数量”的众数吗?中位数呢? (2)全班同学一分钟跳绳的平均数量是多少? (3)如果不知道全班同学总人数,还能求平均数吗? (学生思考,特别是中位数、平均数,教师补充) (给学生时间计算平均数,展示不同计算方法,引出第(3)问) (1)占比最大的数据165个就是众数。那中位数呢?(学生说怎么找)要找中位数首先要排序,这个图里排好了吗?排好了再找最中间,你想整个扇形图是100%,最中间得是百分之多少?50%、51%。那我就从头开始找,一直加到 才够50%,因此中位数就是 。有没有更简单的方法?起始是145这个数,以145为起点,沿着半径把扇形图劈成两半,到这恰好就是50%,这就是中位数。但是这个方法有局限性,能从任意一个位置劈开吗?不行,一定得从排好序的第一个数开始,而且如果这个图不按顺序排,就不能用这个办法了。所以还是第一种办法适用于大多数情况。 (2)(学生可能利用扇形图的百分比算出各项数据对应的人数,之后再计算平均数;也可能不计算出相应人数,直接用各项数据乘以相应百分比)。 (让学生把式子写在黑板上) (一定要对比两种方法!) 其中法一是先把人数算出来,而法二直接乘以的百分比,由于法一中29可以约分,所以两种方法本质上一样,但法二更简单。——追问第(3)问 (3)在法二中并没有用到总人数,也算出了平均数,所以在扇形统计图中不知道总数的情况下仍能计算出平均数。在条形统计图中可以吗?为什么在扇形图中就可以?这些百分比其实就是数据的“权”。看似第二种方法没有除以总数,但实际上是除以了100%。所以可以直接利用各项数据的百分比求平均数。 【议一议】用散点图估计数据的集中趋势 (课本P145) 为了检查面包的质量是否达标,随机抽取了同种规格的面包10个,这10个面包的质量如图所示。 这10个面包质量的众数是多少?中位数是多少? 你能估计出一个这样的面包的平均质量是吗?你是怎么估计的? (1)发现100这条线上的点最多,因此众数是100g;在10个数据中,中位数是第5、第6个数据的平均数,那么就按顺序去数第5、第6个数,因此中位数就是100g。 (2)平均数怎么算? 法一:公式,都加起来再除以10. 法二:以100g为基准,超过100g记为正数、低于100g记为负数,这样计算起来更简单点。 法三:在条形统计图中估算平均数时用到了如果图形轴对称,那么两边数据可以相互中和,那在散点图中看两边的数据能否“中和”。 两边的数据105与95的平均数是100、103与97的平均数是100、101和99的平均数是100,还剩下一个98,它就会把平均水平拉低,平均质量会低于100g.你能想想会低多少吗?总共低了2g,一个十个数据,平均每一个就低了0.2g,因此它的平均质量就是99.8g。 课堂小结 我们今天学习了如何从统计图分析数据的集中趋势,包括平均数、中位数和众数,最好求的是谁?——众数,条形统计图中最高的、扇形统计图中面积最大的就是众数。其次中位数也比较好求,找准最中间是第几个数就好,无论是众数、中位数还是平均数在实际问题中都要带上单位。比较难算的是平均数,但我们能大概估计平均数的大小,只是估计会有误差,如何提高估计的准确度?在每次估计之后,再算一下,从而积累估计的经验。既然还要算,制作统计图有什么用呢?——图形直观。有时候不需要知道精确的平均水平,只要估计大概即可,这就用到了图形,但估计会有误差,需要计算来验证,这就用到了数。所谓“数形结合”就是这个意思。 最后分享给大家一首诗 数与形,本是相依矣 焉能分作两边飞 数缺形时少直观 形少数时难入微 数形结合百般好 割裂分家万事非 切莫忘,几何代数统一体 永远联系切莫离 ——华罗庚 布置作业 以收集同学们的一分钟跳绳数量的调查活动展开,带领学生经历收集数据、整理数据、分析数据的统计过程,调动学习兴趣。 在活动探究一中,利用收集到的数据开展本节课的学习,用EXCEL将数据制作成条形统计图,从而让学生有参与感。 通过三个问题探究从条形统计图中分析数据的集中趋势,其中第(1)问旨在让学生从图中获取数据信息,得出众数和中位数,需要提醒带上单位;第(2)问旨在让学生直观感受图形,大致判断平均收入的大小;第(3)问则是让学生通过计算验证估计是否合理。 【议一议】的目的在于让学生通过条形统计图的几何特征,再次对数据的集中趋势做出大致判断 在活动探究二中,再将收集到的数据制作成扇形统计图,从中分析数据的集中趋势。 结合上两种统计图的分析经验,用散点统计图分析数据的集中趋势。
板书设计 6.3从统计图分析数据的集中趋势 1.条形统计图 平均数 中位数 2.扇形统计图 众数
教学反思 在第一个【议一议】中应当先讲甲队,再讲乙、丙,把乙、丙看成是甲队向左、向右偏移后的。此外,【议一议】部分讲太久了,估计要10min 计算平均数时可以用找基准点的办法简化运算量。 各个环节的时间控制不到位!出现拖堂现象,要严格把握时间,怕讲不完可以设置超链接,直接链接到小结。(绝不能拖堂!) 声音要在大!强调重点时要有突出! 先写课题!!不要在引入后再写!主板不要写草稿! 要有过渡语!在之前我们研究平均数、中位数和众数时都是用数据/数据表来算的,这节课就用统计图分析数据的集中趋势。 检验学生是否掌握时,要让学生举手回答问题,如果大部分学生举手,说明基本都能掌握。 学生试错、出现回答错误可以作为一个亮点,出现错误之后要让其他同学来评价。
1 / 10
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
