5.7三角函数的应用 同步练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含解析)
文档属性
| 名称 | 5.7三角函数的应用 同步练习-2022-2023学年高一上学期数学人教A版(2019)必修第一册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 355.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-12-18 16:09:41 | ||
图片预览



文档简介
高一数学5.7三角函数的应用同步练习
一、选择题(共7题)
如图所示,质点 在半径为 的圆周上按逆时针方向运动,其初始位置为 ,角速度为 ,那么点 到 轴的距离 关于时间 的函数图象大致为
A. B.
C. D.
一根长 的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移 与时间 的函数关系式是 ,其中 是重力加速度,当小球摆动的周期是 时,线长 等于
A. B. C. D.
某种商品一年内每件出厂价在 千元的基础上,按月呈 ( 单位:千元,,,)的模型波动( 为月份, 且 ).已知 月份达到最高价 千元, 月份价格最低为 千元,根据以上条件可确定 的解析式为
A. B.
C. D.
车流量是指单位时间内通过十字路口的车辆数,单位为辆/分,上班高峰期某十字路口的车流量由函数 (其中 )给出, 的单位是辆/分, 的单位是分,则在下列哪个时间段内车流量是增加的
A. B. C. D.
商场人流量被定义为每分钟通过入口的人数,“五一”期间某一天商场的人流量满足函数 ,则人流量增加的时间段是
A. B. C. D.
如图所示为 (,)的一段图象,则 的表达式为
A. B.
C. D.
已知函数 为奇函数,该函数的部分图象如图所示, 是边长为 的等边三角形,则 的值为
A. B. C. D.
二、多选题(共3题)
已知函数 ()的图象关于直线 对称,则
A.函数 为奇函数
B.函数 在 上单调递增
C.若 ,则 的最小值为
D.函数 的图象向右平移 个单位长度得到函数 的图象
记函数 的图象为 ,则下列结论正确的是
A.函数 的最小正周期为
B.函数 在区间 上单调递增
C.直线 是图象 的一条对称轴
D.将函数 的图象向右平移 个单位长度,得到图象
要得到 的图象 ,只要将 图象 怎样变化得到
A.将 的图象 沿 轴方向向左平移 个单位长度
B.将 的图象 沿 轴方向向右平移 个单位长度
C.先作 关于 轴对称图象 ,再将图象 沿 轴方向向右平移 个单位长度
D.先作 关于 轴对称图象 ,再将图象 沿 轴方向向左平移 个单位长度
三、填空题(共5题)
已知某种交流电电流 随时间 的变化规律可以拟合为函数 ,,则这种交流电在 内往复运动的次数为 次.
国际油价 (美元)在某一时间段 (天)内呈现正弦型波动规律 ,现采集到下列信息:最高油价为 美元,当 时达到最低油价,则 的是小值为 .
已知某种交流电电流 随时间 的变化规律可以用函数 , 表示,则这种交流电电流在 内往复运行 次.
下图表示相对于平均海平面的某海湾的水面高度 在某天 时的变化情况,则水面高度 (米)关于时间 (时)的函数解析式为 .
已知 ,,且 在区间 有最小值,无最大值,则 .
四、解答题(共5题)
函数 的部分图象如图所示.
(1) 写出 的最小正周期及图中 , 的值;
(2) 求 在区间 上的最大值和最小值.
如图是半径为 的水车截面图,在它的边缘圆周上有一动点 ,按逆时针方向以角速度 (每秒绕圆心转动 )做圆周运动,已知点 的初始位置为 ,且 ,设点 的纵坐标 是转动时间 (单位:)的函数,记为 .
(1) 写出函数 的解析式,并求 , 的值;
(2) 选用恰当的方法作出函数 , 的简图;
(3) 试比较 ,, 的大小(直接给出大小关系,不用说明理由).
一种波的波形为函数 的图象,若其在区间 上至少有两个波峰(图象的最高点),求正整数 的最小值.
如图,一个水轮的半径为 ,水轮圆心 距离水面 ,已知水轮每分钟转动 圈,如果当水轮上点 从水中浮现(图中点 )时开始计算时间.
(1) 将点 距离水面的高度 表示为时间 的函数;
(2) 点 第一次到达最高点大约需要多少时间?
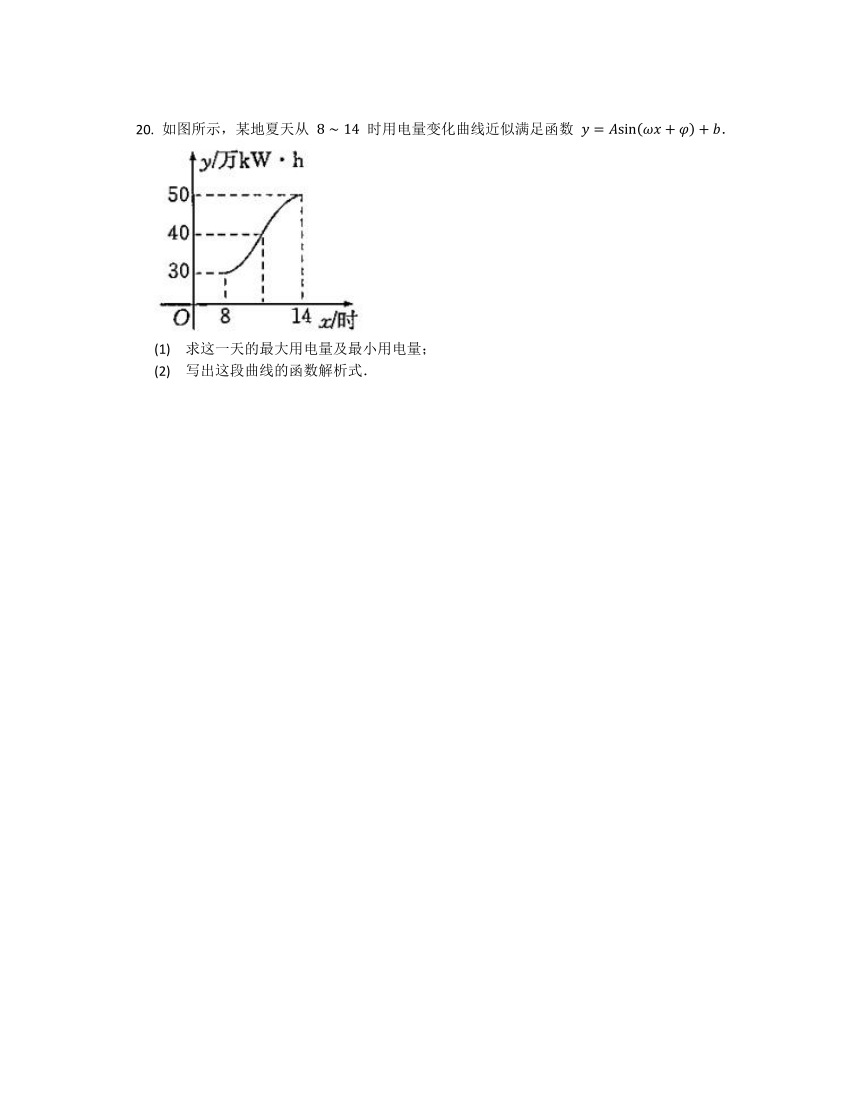
如图所示,某地夏天从 时用电量变化曲线近似满足函数 .
(1) 求这一天的最大用电量及最小用电量;
(2) 写出这段曲线的函数解析式.
答案
一、选择题(共7题)
1. 【答案】C
【解析】解法 :显然,当 时,由已知,得 ,故排除A,D;
又因为质点是按逆时针方向转动,随时间的变化,质点 到 轴的距离 先减小,再排除B.
解法 :根据已知条件,得 ,,.再结合已知,得质点 到 轴的距离 关于时间 的函数为 ,画图得C.
2. 【答案】D
【解析】因为周期 ,
所以 ,
所以 .
3. 【答案】D
【解析】因为 月份达到最高价 千元, 月份价格最低为 千元,
所以当 时,函数 有最大值 ;
当 时,函数 有最小值 ,
所以
所以
函数 的最小正周期 ,由 ,得 .
因为当 时,函数 有最大值,
所以 ,
即 .
因为 ,
所以取 ,得 ,
所以函数 的解析式为 .
4. 【答案】C
【解析】函数 ,
令 ,
得 ,
则函数 在 上单调递增,
当 时,,此时 .
5. 【答案】C
【解析】由 ,,知函数 的单调递增区间为 ,.当 时,.而 .故选C.
6. 【答案】A
【解析】方法一:
由图象可知 ,,
所以 ,即 .
由点 知 ,
所以 .
所以 .故选A.
方法二:
由图象知 ,又图象过点 ,,
且分别为“五点”中的第三点和第五点.
所以
解得 ,,满足 ,
所以 .故选A.
方法三:
因为 ,
所以 ,且 .
所以 的图象是由 向左平移 个单位长度而得到的,
即 .故选A.
方法四:
选项中的 相同,周期相同,仅看平移变换,向左平移 个单位长度,
由选项知 .
故选A.
7. 【答案】C
【解析】因为 为奇函数,
所以 .
因为 ,
所以 ,
所以 .
因为 是边长为 的等边三角形,则 .
又因为函数的周期 ,根据周期公式可得 ,
所以 ,则 .
二、多选题(共3题)
8. 【答案】A;C
【解析】因为直线 是 ()的对称轴,
所以 (),则 ().
当 时,,则 .
对于选项A,,因为 ,所以 为奇函数,故A正确;
对于选项B,(),即 (),当 时, 在 当单调递增,故B错误;
对于选项C,若 ,则 最小为半个周期,即 ,故C正确;
对于选项D,函数 的图象向右平移 个单位长度,即 ,故D错误.
9. 【答案】A;B;C
【解析】函数 的最小正周期为 ,故A选项正确.
由 ,解得 ,所以函数 在区间 上单调递增,故B选项正确.
由于 ,所以直线 是图象 的一条对称轴,故C选项正确.
向右平移 得到 ,故D选项错误.
10. 【答案】A;B;C
三、填空题(共5题)
11. 【答案】
【解析】因为 ,
所以 内往复运动的次数为 (次).
12. 【答案】
【解析】因为 ,,
所以 .
当 时达到最低油价,即 ,
此时 ,.
因为 ,
所以当 时, 取得最小值,
所以 ,
解得 .
13. 【答案】
【解析】因为最小正周期 ,
所以频率为每秒 次,
所以 内往复运行 次.
14. 【答案】 ,
【解析】根据题图可设 ,
则 ,,所以 ,
所以 .
将点 作为“五点法”作图中的第一个点,
则 ,
所以 ,
所以 ,.
15. 【答案】
【解析】由 ,知函数图象的一条对称轴为 ,并且此时 有最小值,即 ,.
又 ,即 ,因此 ,.
四、解答题(共5题)
16. 【答案】
(1) 的最小正周期为 ,,.
(2) 因为 ,所以于是,当 ,即 时, 取得最大值 ;
当 ,即 时, 取得最小值 .
17. 【答案】
(1) 由题意知函数 ,,
所以 ,
.
(2) 根据题意列表:描点、连线,作出函数 , 的简图,如图所示.
(3) .
18. 【答案】由 可知此波形的函数周期为 ,
显然当 时,函数单调递减;
当 时,函数单调递增.
又 时,,
因此自 开始向右的第一个波峰所对的 值为 ,第二个波峰对应的 值为 ,
所以若在区间 上至少有两个波峰,则 的最小值应为 .
19. 【答案】
(1) 如图,建立直角坐标系,设角 是以 为始边, 为终边的角, 每秒钟所转过的角度为 得 .
当 时,,得 即 .
故所求的函数关系式为 .
(2) 令 ,得 .取 ,得 .
故点 第一次到达最高点大约需要 .
20. 【答案】
(1) 最大用电量为 万 ,最小用电量为 万 .
(2) 观察图象可知从 时的图象是 的半个周期的图象,
所以 ,.
因为 ,所以 .所以 .
将 , 代入上式,解得 .
故所求函数解析式为 ,.
一、选择题(共7题)
如图所示,质点 在半径为 的圆周上按逆时针方向运动,其初始位置为 ,角速度为 ,那么点 到 轴的距离 关于时间 的函数图象大致为
A. B.
C. D.
一根长 的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移 与时间 的函数关系式是 ,其中 是重力加速度,当小球摆动的周期是 时,线长 等于
A. B. C. D.
某种商品一年内每件出厂价在 千元的基础上,按月呈 ( 单位:千元,,,)的模型波动( 为月份, 且 ).已知 月份达到最高价 千元, 月份价格最低为 千元,根据以上条件可确定 的解析式为
A. B.
C. D.
车流量是指单位时间内通过十字路口的车辆数,单位为辆/分,上班高峰期某十字路口的车流量由函数 (其中 )给出, 的单位是辆/分, 的单位是分,则在下列哪个时间段内车流量是增加的
A. B. C. D.
商场人流量被定义为每分钟通过入口的人数,“五一”期间某一天商场的人流量满足函数 ,则人流量增加的时间段是
A. B. C. D.
如图所示为 (,)的一段图象,则 的表达式为
A. B.
C. D.
已知函数 为奇函数,该函数的部分图象如图所示, 是边长为 的等边三角形,则 的值为
A. B. C. D.
二、多选题(共3题)
已知函数 ()的图象关于直线 对称,则
A.函数 为奇函数
B.函数 在 上单调递增
C.若 ,则 的最小值为
D.函数 的图象向右平移 个单位长度得到函数 的图象
记函数 的图象为 ,则下列结论正确的是
A.函数 的最小正周期为
B.函数 在区间 上单调递增
C.直线 是图象 的一条对称轴
D.将函数 的图象向右平移 个单位长度,得到图象
要得到 的图象 ,只要将 图象 怎样变化得到
A.将 的图象 沿 轴方向向左平移 个单位长度
B.将 的图象 沿 轴方向向右平移 个单位长度
C.先作 关于 轴对称图象 ,再将图象 沿 轴方向向右平移 个单位长度
D.先作 关于 轴对称图象 ,再将图象 沿 轴方向向左平移 个单位长度
三、填空题(共5题)
已知某种交流电电流 随时间 的变化规律可以拟合为函数 ,,则这种交流电在 内往复运动的次数为 次.
国际油价 (美元)在某一时间段 (天)内呈现正弦型波动规律 ,现采集到下列信息:最高油价为 美元,当 时达到最低油价,则 的是小值为 .
已知某种交流电电流 随时间 的变化规律可以用函数 , 表示,则这种交流电电流在 内往复运行 次.
下图表示相对于平均海平面的某海湾的水面高度 在某天 时的变化情况,则水面高度 (米)关于时间 (时)的函数解析式为 .
已知 ,,且 在区间 有最小值,无最大值,则 .
四、解答题(共5题)
函数 的部分图象如图所示.
(1) 写出 的最小正周期及图中 , 的值;
(2) 求 在区间 上的最大值和最小值.
如图是半径为 的水车截面图,在它的边缘圆周上有一动点 ,按逆时针方向以角速度 (每秒绕圆心转动 )做圆周运动,已知点 的初始位置为 ,且 ,设点 的纵坐标 是转动时间 (单位:)的函数,记为 .
(1) 写出函数 的解析式,并求 , 的值;
(2) 选用恰当的方法作出函数 , 的简图;
(3) 试比较 ,, 的大小(直接给出大小关系,不用说明理由).
一种波的波形为函数 的图象,若其在区间 上至少有两个波峰(图象的最高点),求正整数 的最小值.
如图,一个水轮的半径为 ,水轮圆心 距离水面 ,已知水轮每分钟转动 圈,如果当水轮上点 从水中浮现(图中点 )时开始计算时间.
(1) 将点 距离水面的高度 表示为时间 的函数;
(2) 点 第一次到达最高点大约需要多少时间?
如图所示,某地夏天从 时用电量变化曲线近似满足函数 .
(1) 求这一天的最大用电量及最小用电量;
(2) 写出这段曲线的函数解析式.
答案
一、选择题(共7题)
1. 【答案】C
【解析】解法 :显然,当 时,由已知,得 ,故排除A,D;
又因为质点是按逆时针方向转动,随时间的变化,质点 到 轴的距离 先减小,再排除B.
解法 :根据已知条件,得 ,,.再结合已知,得质点 到 轴的距离 关于时间 的函数为 ,画图得C.
2. 【答案】D
【解析】因为周期 ,
所以 ,
所以 .
3. 【答案】D
【解析】因为 月份达到最高价 千元, 月份价格最低为 千元,
所以当 时,函数 有最大值 ;
当 时,函数 有最小值 ,
所以
所以
函数 的最小正周期 ,由 ,得 .
因为当 时,函数 有最大值,
所以 ,
即 .
因为 ,
所以取 ,得 ,
所以函数 的解析式为 .
4. 【答案】C
【解析】函数 ,
令 ,
得 ,
则函数 在 上单调递增,
当 时,,此时 .
5. 【答案】C
【解析】由 ,,知函数 的单调递增区间为 ,.当 时,.而 .故选C.
6. 【答案】A
【解析】方法一:
由图象可知 ,,
所以 ,即 .
由点 知 ,
所以 .
所以 .故选A.
方法二:
由图象知 ,又图象过点 ,,
且分别为“五点”中的第三点和第五点.
所以
解得 ,,满足 ,
所以 .故选A.
方法三:
因为 ,
所以 ,且 .
所以 的图象是由 向左平移 个单位长度而得到的,
即 .故选A.
方法四:
选项中的 相同,周期相同,仅看平移变换,向左平移 个单位长度,
由选项知 .
故选A.
7. 【答案】C
【解析】因为 为奇函数,
所以 .
因为 ,
所以 ,
所以 .
因为 是边长为 的等边三角形,则 .
又因为函数的周期 ,根据周期公式可得 ,
所以 ,则 .
二、多选题(共3题)
8. 【答案】A;C
【解析】因为直线 是 ()的对称轴,
所以 (),则 ().
当 时,,则 .
对于选项A,,因为 ,所以 为奇函数,故A正确;
对于选项B,(),即 (),当 时, 在 当单调递增,故B错误;
对于选项C,若 ,则 最小为半个周期,即 ,故C正确;
对于选项D,函数 的图象向右平移 个单位长度,即 ,故D错误.
9. 【答案】A;B;C
【解析】函数 的最小正周期为 ,故A选项正确.
由 ,解得 ,所以函数 在区间 上单调递增,故B选项正确.
由于 ,所以直线 是图象 的一条对称轴,故C选项正确.
向右平移 得到 ,故D选项错误.
10. 【答案】A;B;C
三、填空题(共5题)
11. 【答案】
【解析】因为 ,
所以 内往复运动的次数为 (次).
12. 【答案】
【解析】因为 ,,
所以 .
当 时达到最低油价,即 ,
此时 ,.
因为 ,
所以当 时, 取得最小值,
所以 ,
解得 .
13. 【答案】
【解析】因为最小正周期 ,
所以频率为每秒 次,
所以 内往复运行 次.
14. 【答案】 ,
【解析】根据题图可设 ,
则 ,,所以 ,
所以 .
将点 作为“五点法”作图中的第一个点,
则 ,
所以 ,
所以 ,.
15. 【答案】
【解析】由 ,知函数图象的一条对称轴为 ,并且此时 有最小值,即 ,.
又 ,即 ,因此 ,.
四、解答题(共5题)
16. 【答案】
(1) 的最小正周期为 ,,.
(2) 因为 ,所以于是,当 ,即 时, 取得最大值 ;
当 ,即 时, 取得最小值 .
17. 【答案】
(1) 由题意知函数 ,,
所以 ,
.
(2) 根据题意列表:描点、连线,作出函数 , 的简图,如图所示.
(3) .
18. 【答案】由 可知此波形的函数周期为 ,
显然当 时,函数单调递减;
当 时,函数单调递增.
又 时,,
因此自 开始向右的第一个波峰所对的 值为 ,第二个波峰对应的 值为 ,
所以若在区间 上至少有两个波峰,则 的最小值应为 .
19. 【答案】
(1) 如图,建立直角坐标系,设角 是以 为始边, 为终边的角, 每秒钟所转过的角度为 得 .
当 时,,得 即 .
故所求的函数关系式为 .
(2) 令 ,得 .取 ,得 .
故点 第一次到达最高点大约需要 .
20. 【答案】
(1) 最大用电量为 万 ,最小用电量为 万 .
(2) 观察图象可知从 时的图象是 的半个周期的图象,
所以 ,.
因为 ,所以 .所以 .
将 , 代入上式,解得 .
故所求函数解析式为 ,.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
