第1章特殊的四边形复习课（共2课时）

第1章特殊的四边形复习课（第1课时）
学习目标：
1、熟练掌握特殊四边形的性质和判定，并能应用其解决相关问题。
2、熟练运用综合法证明几何题，建立空间观念，发展学生几何推理能力。
学习重难点：
1、熟练掌握特殊四边形的性质和判定，并能应用其解决相关问题。
2、尝试添加辅助线，帮助解决问题。
学习过程：
一、知识回顾
1. 平行四边形的性质
（1）平行四边形对边______，对角__ ___；对角线___ ___；邻角___ ___.
（2）平行四边形两个邻角的平分线互相______，两个对角的平分线互相_____。
（3）平行四边形的面积公式________________.
2．平行四边形的判定
（1）定义：__________ .
（2）边：_____________________或___________________．
（3）角：__________ _________．
（4）对角线：_____________ ________．
3. 特殊的平行四边形的性质
边 角 对角线 对称性
矩形
菱形
正方形
4．特殊的平行四边形的判别方法
（1）菱形的判定：①_______边都相等的四边形菱形．②__________的平行四边形是菱形．③__________的平行四边形是菱形．
（2）矩形的判定：①有___个是直角的四边形是矩形．②______________的平行四边形是矩形．③______________的平行四边形是矩形．
（3）正方形的判定：有___个是直角的 形是正方形；有 相等的 形是正方形。对角线 的四边形是正方形。
5．等腰梯形的性质：边____________________ ____.
角_______ __________________.
对角线_________ _______________.
6.等腰梯形的判别方法
①定义： _____________.
②角：_______________ ____________ _________．
③对角线： _____________．
二、对应训练
1、一个菱形的两条对角线分别是6cm，8cm，则这个菱形的周长等于 cm，面积是 cm2
2、如图，矩形ABCD的两条对角线相交于O，∠AOD=120°，AB=4cm，则矩形对角线AC长__cm．
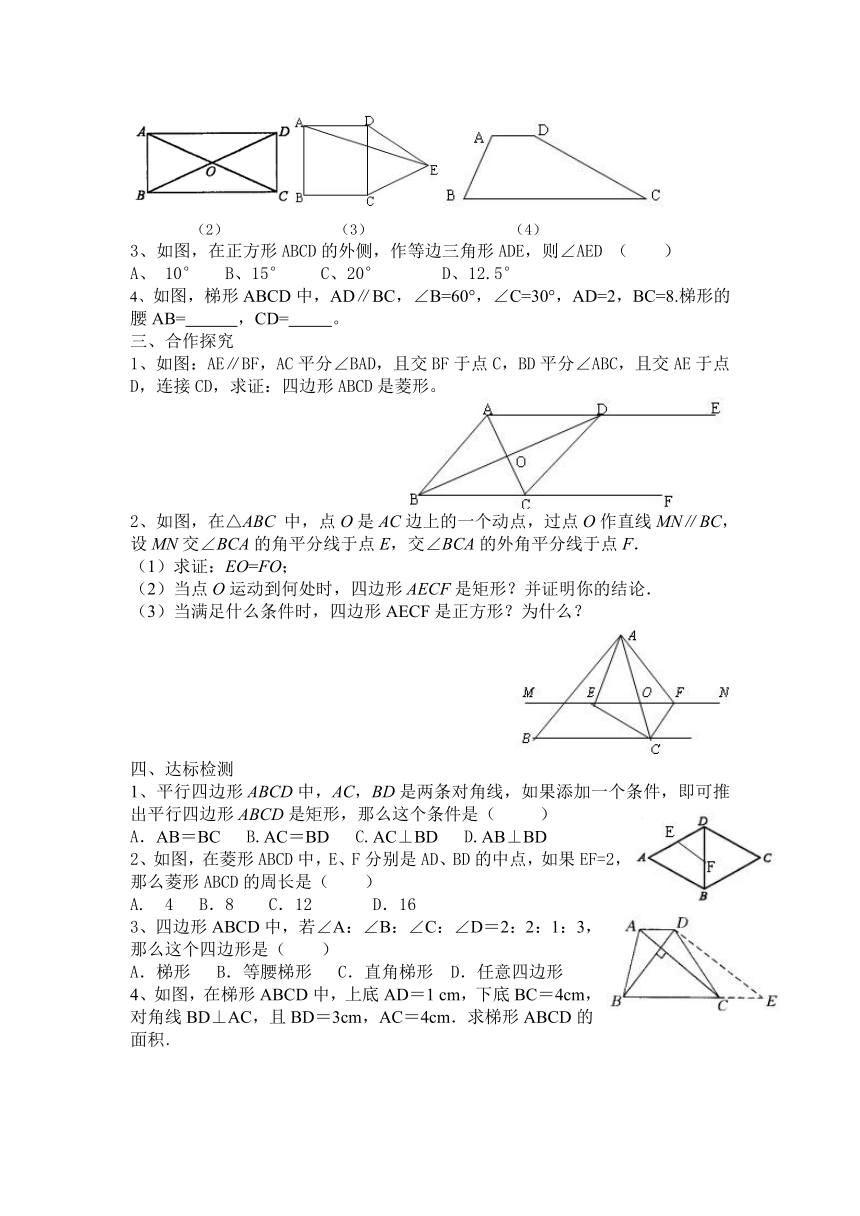
（2） （3） （4）
3、如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AED （ ）
A、 10° B、15° C、20° D、12.5°
4、如图，梯形ABCD中，AD∥BC，∠B=60°，∠C=30°，AD=2，BC=8.梯形的腰AB= ，CD= 。
三、合作探究
1、如图：AE∥BF，AC平分∠BAD，且交BF于点C，BD平分∠ABC，且交AE于点D，连接CD，求证：四边形ABCD是菱形。
2、如图，在△ABC 中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的角平分线于点E，交∠BCA的外角平分线于点F．
（1）求证：EO=FO；
（2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论．
（3）当满足什么条件时，四边形AECF是正方形？为什么？
四、达标检测
1、平行四边形ABCD中，AC，BD是两条对角线，如果添加一个条件，即可推出平行四边形ABCD是矩形，那么这个条件是（ ）
A．AB＝BC B.AC＝BD C.AC⊥BD D.AB⊥BD
2、如图，在菱形ABCD中，E、F分别是AD、BD的中点，如果EF=2，那么菱形ABCD的周长是（ ）
A. 4 B．8 C．12 D．16
3、四边形ABCD中，若∠A：∠B：∠C：∠D＝2：2：1：3，那么这个四边形是（ ）
A．梯形 B．等腰梯形 C．直角梯形 D．任意四边形
4、如图，在梯形ABCD中，上底AD＝1 cm，下底BC＝4cm，对角线BD⊥AC，且BD＝3cm，AC＝4cm．求梯形ABCD的面积．
第1章特殊的四边形复习课（第2课时）
学习目标：
1、会判断中心对称图形，熟记中位线定理。
2、能综合应用本章的定理进行计算和证明。
3、理解特殊四边形的性质和判定也是证明两角相等、两线段相等、平行和垂直的方法之一。
学习过程
一、知识回顾
1、什么是中心对称图形？2、三角形的中位线、梯形的中位线定理是什么？
二、对应练习
1、下列图形中不是中心对称图形的有（ ）
A.1个 B.2个 C.3个 D.4个
2、如图，AB∥CD，E，F分别为AC，BD的中点，若AB=5，CD=3，则EF的长是（　　）
A．4 B．3 C．2 D．1
3、如图，梯形ABCD中，AD∥BC，EF是梯形的中位线，对角线AC交EF于G，若BC=10cm，EF=8cm，则GF的长等于 cm。
（2题图） （3题图） （三、1题图）
三、合作探究，交流展示
1、如图所示，在梯形ABCD中，AD∥BC，点E、F分别为AB、CD的中点．连接AF并延长，交BC的延长线于点G．
（1）求证：△ADF≌△GCF；
（2）若EF=7.5，BC=10，求AD的长．
四、启发引导，精讲点拨
1、如图，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，延长BN交AC于点D，已知AB=10，BC=15，MN=3
（1）求证：BN=DN；
（2）求△ABC的周长．
五、系列训练，当堂达标
1．下列图形：平行四边形、矩形、菱形、等腰梯形、正方形中既是轴对称图形又是中心对称图形的有（ ）个
A、1 B、2 C、3 D、4
2．若O是四边形ABCD对角线的交点且OA=OB=OC=OD，则四边形ABCD是
A、等腰梯形 B、矩形 C、正方形 D、菱形
3、下面性质中菱形有而矩形没有的是（ ）
A、邻角互补 B、内角和为360°C、对角线相等 D、对角线互相垂直
4、已知菱形的两条对角线长分别是4和8，则菱形的面积是（ ）
A、32 B、64 C、16 D、32
5、顺次连结任意四边形四边中点所得的四边形一定是（ ）
A：平行四边形 B：矩形 C：菱形 D：正方形
6、下列命题中，不成立的是（ ）．
A、等腰梯形的两条对角线相等 B、菱形的对角线平分一组对角
C、顺次连结四边形的各边中点所得的四边形是平行四边形
D、两条对角线互相垂直且相等的四边形是正方形
7、如图，菱形ABCD的对角线AC、BD相交于点O，AE∥BD，BE∥AC，AE、BE相交于点E，求证：OAEB是矩形。
8、如图，以△ABC的三边为边在BC的同侧分别作三个等边三角形，即△ABD、△BCE、△ACF，请回答下列问题：
（1）四边形ADEF是什么四边形？并说明理由
（2）当△ABC满足什么条件时，四边形ADEF是菱形？
（3）当△ABC满足什么条件时，四边形ADEF是矩形？
（4）当△ABC满足什么条件时，以A、D、E、F为顶点的四边形不存在．
六、回扣目标，总结反思
通过本节课的学习你有什么收获和感想？