1.3特殊的平行四边形（共4课时）

1.3 特殊的平行四边形（第1课时）
学习目标：
1、理解矩形的意义，知道矩形与平行四边形的区别与联系。
2、掌握矩形的性质定理，会用定理进行有关的计算与证明。
3、掌握直角三角形斜边上中线的性质与应用。
学习重点：掌握矩形的性质定理，会用定理进行有关的计算与证明。
学习难点：掌握直角三角形斜边上中线的性质与应用
学习过程：
一、情景导入，目标定向：
列举生活中矩形（即长方形）的实例，例如： 等，都给我们以矩形的形象。矩形是特殊的平行四边形，它除了具有平行四边形的所有性质外，还具有哪些特殊的性质呢？
二、学案引领，自主学习
阅读教材13页—15页内容完成以下题目：
1、 叫做矩形。矩形是________的平行四边形。
2、从矩形的意义可以探究矩形具有的性质：
（1）矩形具有平行四边形的一切性质。
（2）矩形与平行四边形比较又有其特殊的性质:
特殊在“角”上的性质是_____________________________________________.
特殊在“对角线”上的性质是：_______________________________________.
3、从矩形的性质可以说明：直角三角形斜边上的中线等于斜边的________.
三、合作探究，交流展示
1、将一个矩形纸片沿对称轴进行折叠，发现矩形的四个角有什么关系？如何利用矩形的定义及平行线的性质进行证明？
2、度量矩形的两条对角线的长，你有什么发现？如何利用矩形的定义及平行线的性质进行证明？
已知：如图，四边形ABCD是矩形。求证：AC=BD。
3、将（2）中的矩形沿对角线AC剪开，会得到两个什么图形？这时OB或OD的长度与边AC的长度有什么关系？怎样证明你的结论？
四、启发引导，精讲点拨
如图，矩形ABCD的对角线AC=8cm，∠AOD=120°，求AB的长。
（分析：根据矩形的对角线相等且互相平分可得AO=BO=AC，再根据邻角互补求出∠AOB的度数，然后得到△AOB是等边三角形，再根据等边三角形的性质即可得解．）
五、系列训练，当堂达标
1、矩形的两条对角线的夹角为60°，较短的边长为4.5厘米，则对角线长为 。
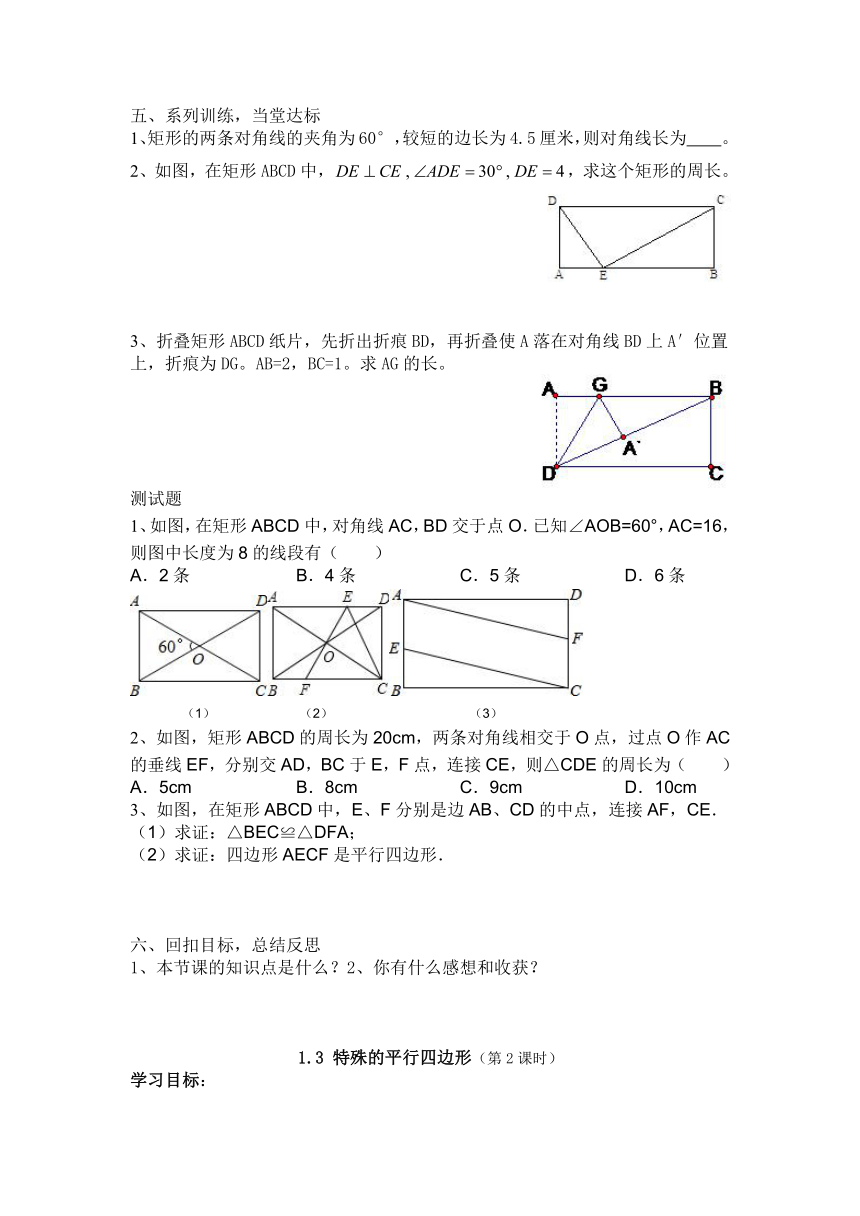
2、如图，在矩形ABCD中，，求这个矩形的周长。
3、折叠矩形ABCD纸片，先折出折痕BD，再折叠使A落在对角线BD上A′位置上，折痕为DG。AB=2，BC=1。求AG的长。
测试题
1、如图，在矩形ABCD中，对角线AC，BD交于点O．已知∠AOB=60°，AC=16，则图中长度为8的线段有（　　）
A．2条 B．4条 C．5条 D．6条
（1） （2） （3）
2、如图，矩形ABCD的周长为20cm，两条对角线相交于O点，过点O作AC的垂线EF，分别交AD，BC于E，F点，连接CE，则△CDE的周长为（　　）
A．5cm B．8cm C．9cm D．10cm
3、如图，在矩形ABCD中，E、F分别是边AB、CD的中点，连接AF，CE．
（1）求证：△BEC≌△DFA；
（2）求证：四边形AECF是平行四边形．
六、回扣目标，总结反思
1、本节课的知识点是什么？2、你有什么感想和收获？
1.3 特殊的平行四边形（第2课时）
学习目标：
1、能应用矩形定义、判定定理，解决简单的证明和计算，进一步培养分析能力。
2、培养综合应用知识分析解决问题的能力。
学习重点：应用矩形定义、判定定理，解决简单的证明和计算。
学习难点：培养综合应用知识分析解决问题的能力
学习过程：
一、复习导入，目标定向
矩形的定义是什么？应用定义可以判定一个平行四边形是不是矩形，此外还有其他方法吗？
二、学案引领，自主学习
自学教材16页—17页内容完成以下题目：
1、运用定义证明一个平行四边形是矩形，只需证明__________________.
2、矩形相对于一般平行四边形来讲，特殊在“对角线”和“角”上。通过自学，我们可以从“对角线”和“角”两方面得到矩形的判定定理：
矩形的判定定理（1）：________________________________________________.
矩形的判定定理（2）：________________________________________________.
三、合作探究，交流展示
如何证明“对角线相等的平行四边形是矩形”呢？现在唯一的途径就是利用定义。尝试着把证明过程写在下面：
已知：在ABCD中，AC=BC。求证：ABCD是矩形。
四、启发引导，精讲点拨
例题：如图，M、N分别是平行四边形ABCD对边AD、BC的中点，且AD=2AB，求证：四边形PMQN是矩形。
【分析：（1）从条件出发：由M、N分别是平行四边形ABCD对边AD、BC的中点，且AD=2AB，我们很容易得到AM=________,从而得到∠AMB=∠_______.又因为AD∥BC,可得∠AMB=∠_______，所以可得∠_______=∠_______。同理可得∠BAN=∠MAN. (2)要证四边形PMQN是矩形，根据矩形的判定定理，可证四边形PMQN有三个角是直角。】
根据分析完成证明：
五、系列训练，当堂达标
1、在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是某合作学习小组的4位同学拟定的方案，其中正确的是（ ）．
A．测量对角线是否相互平分 B．测量两组对边是否分别相等
C．测量一组对角是否都为直角 D．测量其中三个角是否都为直角
2、能判断四边形是矩形的条件是（ ）
A、两条对角线互相平分 B、两条对角线相等
C、两条对角线互相平分且相等 D、两条对角线互相垂直。
3、如图,EB=EC,EA=ED,AD=BC, ∠AEB=∠DEC,证明:四边形ABCD是矩形.
测试题
1、如图， ABCD的对角线相交于点O，请你添加一个条件 （只添一个即可），使 ABCD是矩形．
（1） （2） （3）
2、如图，在平行四边形ABCD中，对角线AC和BD相交于点O，则下面条件能判定平行四边形ABCD是矩形的是（　　）
A．AC=BD B．AC⊥BD C．AC=BD且AC⊥BD D．AB=AD
3、已知：如图，四边形ABCD的对角线AC、BD交于点O，BE⊥AC于E，DF⊥AC于F，点O既是AC的中点，又是EF的中点．
（1）求证：△BOE≌△DOF；
（2）若OA=BD，则四边形ABCD是什么特殊四边形？说明理由．
六、回扣目标，总结反思
1、综合两节课的学习，矩形是特殊的平行四边形特殊在哪里？
2、矩形的判定方法共有几个？哪几个？
1.3 特殊的平行四边形-菱形（第3课时）
学习目标：
1、理解菱形的定义。2、探究归纳菱形的性质。
3、掌握菱形的判定方法。4、培养综合运用知识分析解决问题的能力。
学习重点：理解菱形的定义。探究归纳菱形的性质。掌握菱形的判定方法。
学习难点：培养综合运用知识分析解决问题的能力。
学习过程：
一、情景导入，目标定向
列举生活中菱形的实例，例如： 等，都给我们以菱形的形象。菱形是特殊的平行四边形，它除了具有平行四边形的所有性质外，还具有哪些特殊的性质呢？
二、学案引领，自主学习
自学教材17页—19页内容完成以下题目：
1、 叫做菱形。菱形是________的平行四边形。
2、从菱形的定义可以探究菱形的性质：
（1）菱形具有平行四边形的一切性质。
（2）菱形与平行四边形比较又有其特殊的性质:
特殊在“边”上的性质定理1是_____________________________________________.
特殊在“对角线”上的性质定理2是：_______________________________________.
3、我们可以从“对角线”和“边”两方面得到菱形的判定定理：
菱形的判定定理（1）：________________________________________________.
菱形的判定定理（2）：________________________________________________.
三、合作探究，交流展示
1、将一张菱形纸片沿对称轴进行折叠，发现菱形的四条边有什么关系？对角线有什么关系？如何利用菱形的定义及平行线的性质进行证明？
2、性质定理1的逆命题是什么？是真命题吗？如何证明？
3、说出“菱形的对角线互相垂直”的逆命题，并证明。
已知：在ABCD中，AC，BD相交于点O，AC⊥BD，求证：ABCD是菱形。
四、启发引导，精讲点拨
将宽度为1的两张纸条交叉重叠在一起，重叠的部分组成了四边形ABCD。
（1）四边形ABCD是菱形吗？为什么？
（2）如果∠ABC=30°，你会求出ABCD的面积吗？
五、系列训练，当堂达标
1、菱形周长为40，一条对角线长为16，则另一条对角线长为 ,这个菱形的面积为 。
2、如图，ABCD是对角线互相垂直的四边形，且OB=OD，请你添加一个适当的条件 ，使ABCD成为菱形（只需添加一个即可）
（2） （3） （4）
3、用直尺和圆规作一个以线段AB为边的菱形，作图痕迹如图所示，能得到四边形ABCD是菱形的依据是（　　）
A．一组邻边相等的四边形是菱形 B．四边相等的四边形是菱形
C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形
4、如图，△ABC中，AB=AC，AD是△ABC外角的平分线，已知∠BAC=∠ACD．
（1）求证：△ABC≌△CDA；
（2）若∠B=60°，求证：四边形ABCD是菱形．
测试题
1、如图，在菱形ABCD中，对角线AC与BD交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（　　）
A．75° B．65° C．55° D．50°
2、如图，在菱形ABCD中，DE⊥AB于点E，cosA=，BE=4，则tan∠DBE的值是 ．
3、如图，矩形ABCD的对角线相交于点O，DE∥CA，AE∥BD．
（1）求证：四边形AODE是菱形；
（2）若将题设中“矩形ABCD”这一条件改为“菱形ABCD”，其余条件不变，则四边形AODE是 。
六、回扣目标，总结反思
1、回顾本课的学习，菱形是特殊的平行四边形特殊在哪里？
2、菱形的判定方法共有几个？哪几个？
1.3 特殊的平行四边形（第4课时）
学习目标
1．掌握正方形的概念、性质和判定，并会用它们进行有关的论证和计算．
2．理解正方形与平行四边形、矩形、菱形的联系和区别。
学习重点：掌握正方形的概念、性质和判定，并会用它们进行有关的论证和计算
学习难点：理解正方形与平行四边形、矩形、菱形的联系和区别。
学习过程：
一、情景导入，目标定向
1、你能从一张矩形纸片上剪出一个正方形吗？
2、列举生活中正方形的实例，例如： 等，都给我们以正方形的形象。正方形是特殊的矩形也是特殊的菱形，它具有哪些特殊的性质呢？
二、学案引领，自主学习
自学教材19页—20页内容完成以下题目：
1、 叫做正方形。正方形是________的矩形，也是_______的菱形。
2、从正方形的意义可以探究正方形具有的性质：
（1）正方形具有平行四边形的一切性质。
（2）正方形具有矩形的一切性质。
（3）正方形具有菱形的一切性质。
（4）正方形的对角线具有的性质是___________________________________.
3、正方形的判定方法是：
（1）_____________________________________的矩形是正方形。
（2）_____________________________________的菱形是正方形。
三、合作探究，交流展示
（1）正方形有几条对称轴？
（2）正方形的边、角、对角线各具有什么性质？
（3）具备什么条件的菱形是正方形？
（4）怎样判断一个平行四边形是正方形？怎样判断一个四边形是正方形？
四、启发引导，精讲点拨
1、如图，正方形ABCD中，对角线AC，BD相交于点O，
（1）求∠ACB的度数。
（2）图中有哪些全等的直角三角形，把它们分别写出来。
2、已知：如图，△ABC中，∠C=90°，CD平分∠ACB，DE⊥BC于E，DF⊥AC于F．求证：四边形CFDE是正方形．
五、系列训练，当堂达标
1、正方形的四条边____ __，四个角___ ____，两条对角线____ ____．
2、在四边形ABCD中，O是对角线的交点，能判定这个四边形是正方形的是（ ）
（A）AC=BD，AB∥CD，AB=CD （B）AD∥BC，∠A=∠C
（C）AO=BO=CO=DO，AC⊥BD （D）AO=CO，BO=DO，AB=BC
3、下列说法是否正确。
①对角线相等的菱形是正方形；（ ）②对角线互相垂直的矩形是正方形；（ ）
③对角线垂直且相等的四边形是正方形；（ ）
④四条边都相等的四边形是正方形；（ ）⑤四个角相等的四边形是正方形．（ ）
4、已知：如图，点E是正方形ABCD的边CD上一点，点F是CB的延长线上一点，且DE=BF．求证：EA⊥AF．
5、已知：如图，正方形ABCD中，对角线的交点为O，E是OB上的一点，DG⊥AE于G，DG交OA于F．求证：OE=OF
测试题
1、如图，在正方形ABCD的外侧，作等边三角形ADE，连接BE，则∠AEB的度数为（ ） A．10° B．15° C．20° D．12.5°
2、如图，已知正方形ABCD的边长为1，连接AC、BD，CE平分∠ACD交BD于点E，则DE= 。
3、如图，点O是线段AB上的一点，OA=OC，OD平分∠AOC交AC于点D，OF平分∠COB，CF⊥OF于点F．
（1）求证：四边形CDOF是矩形；
（2）当∠AOC多少度时，四边形CDOF是正方形？并说明理由．
、
六、回扣目标，总结反思
1、回顾本课的学习，正方形是特殊的矩形、菱形和平行四边形，特殊在哪里？
2、正方形的判定方法共有几个？哪几个？